控制性結構面對地下洞室圍巖穩定性的影響

巨能攀 趙建軍 黃潤秋 孫傳敏

(成都理工大學“地質災害防治與地質環境保護”國家重點實驗室,成都610059)

一般而言,巖體結構面是自然地質歷史過程的產物,結構面規模越大,對工程的控制和影響就越大,它們往往關系到山體、巖體和區域構造穩定性,影響和控制工程結構形式、布置和選點,控制巖體破壞形式,對工程整體穩定性影響較大[1]。規模越小的結構面主要控制巖體破壞形式,對工程局部穩定性有一定的影響。基體裂隙則主要影響巖體的完整性、力學特性、滲透性并決定巖體的破壞形式,對工程穩定性影響不突出[2,3]。所以控制性結構面主要是對地下洞室布置和圍巖穩定性起控制作用的大規模斷層或軟弱夾層。

眾多學者研究了結構面對地下洞室圍巖穩定的影響,但已有的成果主要集中在具體工程和具體工程特性的結構面對圍巖穩定性影響方面[4～7]。針對結構面對地下洞室布置和圍巖穩定影響的宏觀規律還沒有取得比較系統的成果,僅有些局限于實踐基礎上的經驗,如“陡傾結構面對圍巖穩定性影響較小,而緩傾影響較大”等,還沒有對結構面與工程布置和圍巖穩定性的相互作用關系做詳細的研究。本文以糯扎渡水電站的地下洞室群為原型,在眾多的結構面中,選取兩類典型的結構面,分別詳細分析它們對地下廠房圍巖應力、變形的影響,總結出控制性斷層和主要結構物的距離與結構物應力和變形的關系,以及不同產狀的結構面對圍巖應力和應變影響的定量關系。其成果對其他類似的洞室群的布置和形態、結構設計具有一定的指導意義。

1 地質條件及結構面工程特性

糯扎渡水電站壩高261.5 m,裝機容量5 850 MW。電站采用左岸地下發電系統,其地下發電系統主要由主廠房(418 m ×29 m×77.7 m)、主變開關室、尾水調壓室以及尾水洞等構成了龐大而復雜的地下洞室群。

地下洞室群的主體巖性為二疊紀-三疊紀花崗巖,690～810 m海拔高度以上為緩傾坡內的中三疊統忙懷組下段砂巖、泥巖[8,9]。地下廠房區地應力實測結果,最大主應力量值為6.55～11.41 MPa,方向大致為 N20°～65°E。大量的現場調查表明,研究區發育有三類結構面。其中Ⅰ類結構面為具有一定寬度構造巖充填的控制性斷層型結構面,其總體特征表現不僅在規模上具有一定的延伸長度(一般貫穿整個壩區,延伸長度在100 m以上),而且具有一定厚度的斷層破碎帶,破碎帶物質多由性狀相對較差的各類構造巖組成。因而這類結構面對巖體的變形破壞起著關鍵性的控制作用。其巖體力學效應和強度特征主要受充填物的性質和厚度控制。根據其規模,這類結構面又可進一步分為兩級：①延伸長度在1 km以上(Ⅰ-1);②延伸長度在0.1～1 km 之間(Ⅰ-2)。顯然,這類結構面對工程巖體穩定性的控制范圍不同,因而具有不同的工程意義。Ⅰ類結構面展布特征如圖1所示,其工程特性如表1所列。

2 Ⅰ-1類結構面對地下洞室群布置的控制

2.1 地下洞室的選址和布置基本要求

水電站地下洞室的位置選擇應以地下廠房為主,兼顧其他洞室,綜合巖性、巖體結構特性、軟弱地質結構面的空間展布、風化卸荷深度、地應力狀態及水文地質條件,確定地下廠房的臨河距離、埋置深度及空間位置[10]。一般而言,巖體結構較差且地應力較低時,廠房軸線的確定以巖體結構條件為主;當巖體結構較好,且地應力值較高時,應考慮地應力因素為主。按照一般要求,廠房選址時應避開Ⅰ級結構面,盡量避開Ⅱ級結構面。廠房軸線的方向與廠區初始地應力場最大主應力方向的夾角不宜過大,一般要求小于30°。

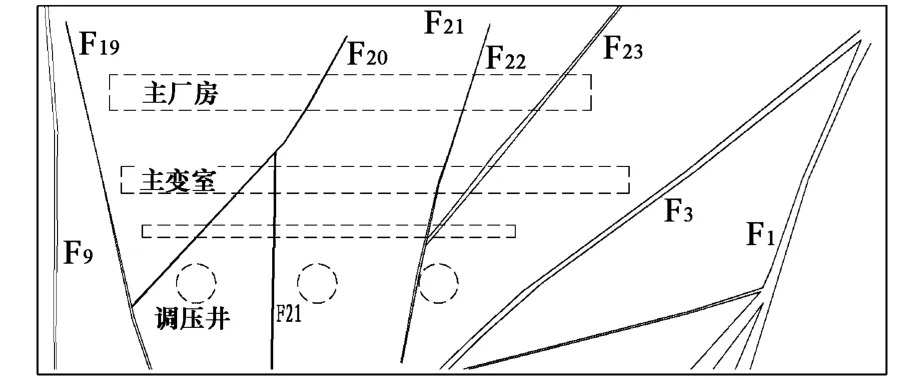
圖1 結構面展布特征Fig.1 Distribution character of main discontinuities

2.2 糯扎渡地下洞室群的布置

糯扎渡水電站引水發電系統布置于左岸山體中,廠區由主廠房、主變室、尾水閘門室及尾水調壓室等構成,主要洞室的山體覆蓋厚度約為180～220 m,距坡面的水平距離在250 m左右。引水系統包括引渠、進水口、壓力管道等建筑物,發電機組均為單機單管引水[11]。按照前述的地下洞室布置原則,需要盡可能增加地下洞室群與F1和F3斷層距離;但由于廠房區的構造格架、地質條件和建設規模的限制,廠房區主要的四大洞室群沒有向外移動的余地,通過多種方案的分析研究,確定以減少主廠房的長度和通過壓縮洞室間距的方法使得洞室群盡量遠離F3和F1斷層。何種距離最利于洞室的穩定?本文擬以洞室群的主廠房為原型,采用Flac3D數值模擬方法[11～13]來研究F3、F1斷層與洞室邊墻不同距離時廠房的應力和應變特性,得到距離和洞室群穩定性的相互關系。

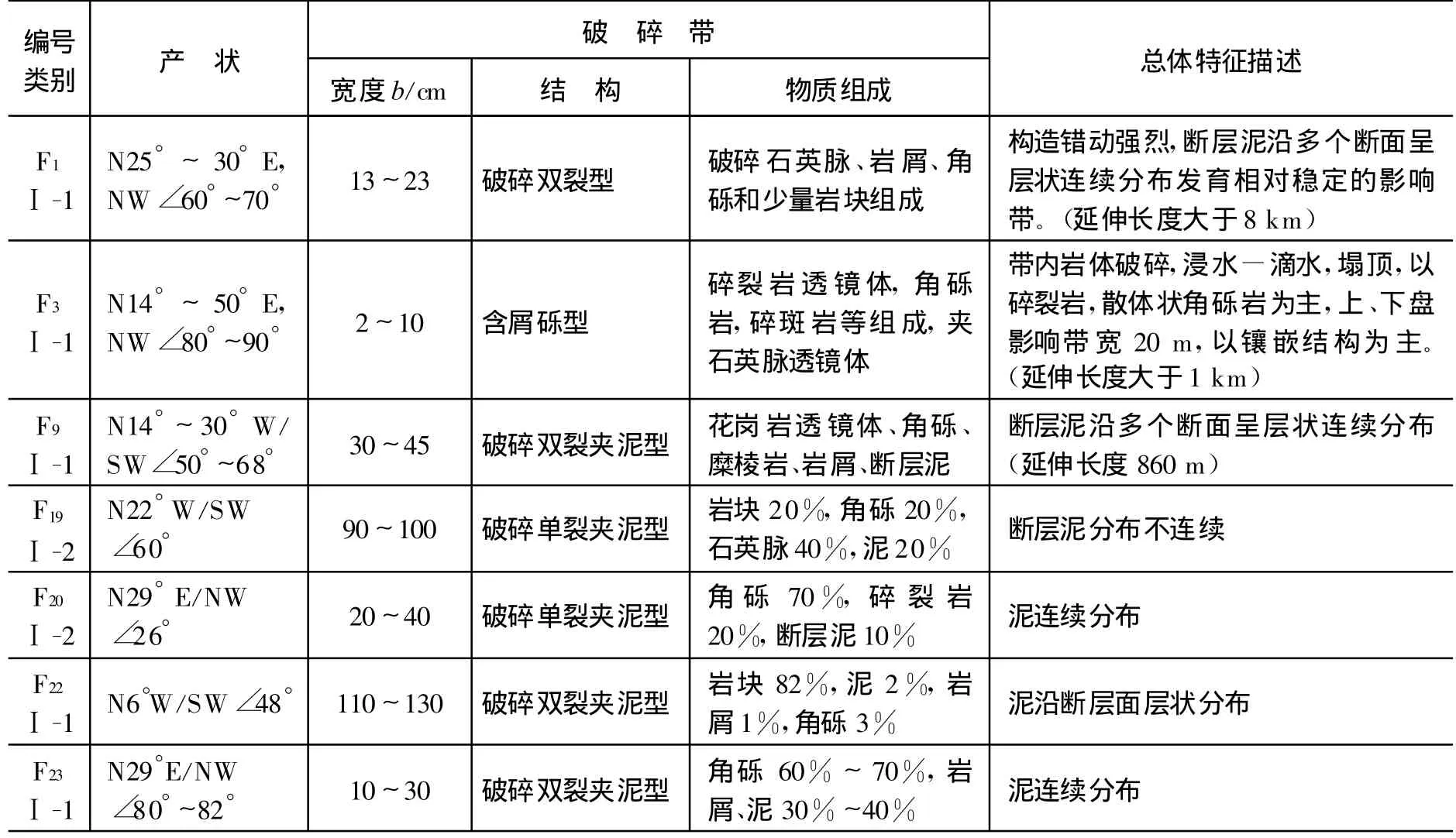
表1 Ⅰ類結構結構面的工程特性Table 1 Engineering characteristics of typical TypeⅠjoints

2.3 計算模型及其模擬方案設計

糯扎渡水電站的主廠房位于壩區左岸,其垂直埋深約200 m,外側端墻距坡面距離近250 m。其廠房區巖體主要為塊狀、次塊狀的花崗巖,總體上巖體為Ⅱ類巖體,和從廠房的北東側通過。地下廠房和F3,F1的關系如圖1所示,建立的計算模型如圖2所示。

主廠房區主要為Ⅱ類花崗巖,F1和F3為斷層型Ⅰ-1結構面。巖體和斷層的取值如表2所示[4,5,12]。

共建立15個模型進行對比。整個洞室的內端墻到F3的距離從180 m變化到40 m,每個模型的內端墻到F3的距離相差1 0m,記下每個模型開挖后如圖3所示追蹤點的位移和應力值,然后進行對比分析。

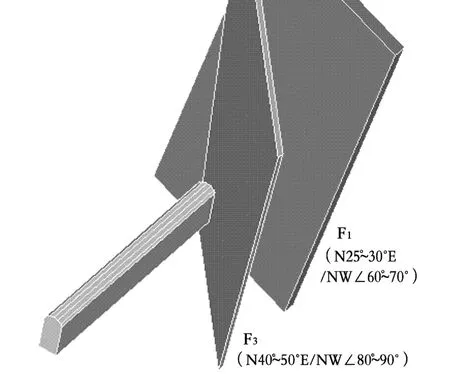
圖2 主廠房與F1,F3相互關系Fig.2 Relation between the main plant and F1,F3

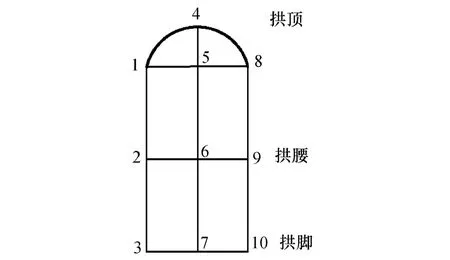
圖3 追蹤點布置示意圖Fig.3 The layout of tracking points

2.4 模擬結果分析

地下洞室開挖后,圍巖在初始應力場的作用下向廠房的臨空面發生了一定的位移,同時圍巖的應力場也發生了變化;特別是隨著洞室與F1和F3的距離減小,在洞室的端墻附近產生了較大的應力集中,其位移值也出現較明顯的變化。

2.4.1 應力隨距離動態變化分析

地下洞室開挖后,圍巖的應力場發生了變化(圖4、圖5)。為了準確了解各距離條件下應力的變化狀況,在模擬計算過程中,利用Flac3D的Fish語言,開發了記錄各個追蹤點應力并自動保存為外部文件的實用程序,以此做出各個追蹤點的應力變化曲線來進行對比分析,如洞室2#追蹤點應力隨端墻距離的變化曲線(圖6)。

綜合以上各點的應力隨內端墻與F3距離的變化特征可看出,不同工程部位F3的影響效果有一定的差異,如頂拱隨著距離的變化,應力變化規律不明顯,最大(小)主應力都在一定范圍附近內波動。其他各點總體上表現為：F3對洞室圍巖應力產生較大影響的距離主要在80 m以內,對應力的影響主要呈現出最大主應力不斷增加,而最小主應力逐漸減小,使得應力差加速增大而影響洞室的圍巖穩定,如內端墻中部2#(圖6)。對圍巖最大主應力隨端墻到距離的變化進行了統計得到如圖7所示曲線,從中也可以體現端墻應力隨距離的變化規律,應力最大值隨內端墻距F3距離的減小而增大,特別是80 m后增大較快,最大增值近2倍。

表2 巖體和斷層物理力學參數Table 2 Physical and mechanical parameters of rock mass and faults

圖4 模型15最大主應力等值線圖Fig.4 Contour of the max stress in Model 15

圖5 模型15最小主應力等值線圖Fig.5 Contour of the min stress in M odel 15

2.4.2 位移隨距離動態變化分析

地下洞室開挖后,圍巖將產生位移變化(圖8)。為準確了解各距離條件下位移的變化狀況,同樣開發了記錄各個追蹤點位移并自動保存為外部文件的實用程序,以此做出各個追蹤點的位移變化曲線并進行對比分析,如洞室6#追蹤點位移隨端墻距離的變化曲線(圖8)。

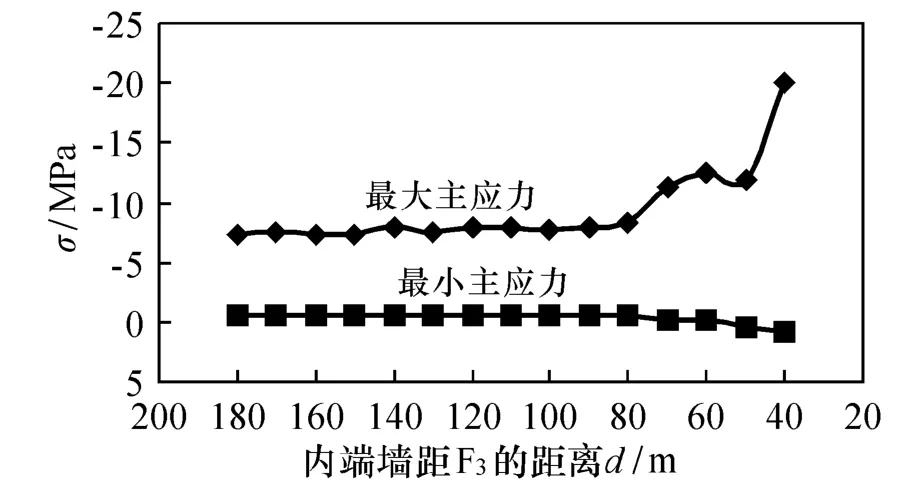
圖6 內端墻中部(2#)應力隨端墻距離變化曲線Fig.6 Curve between stress and distance of 2#

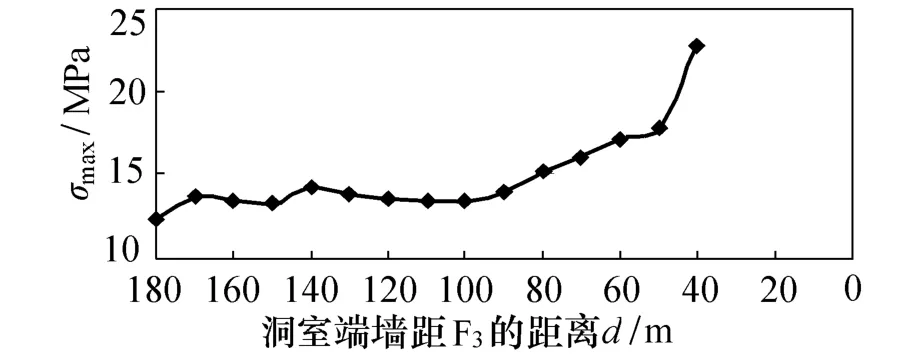
圖7 圍巖應力最大值隨端墻距離變化曲線Fig.7 Curve between max of stress and distance

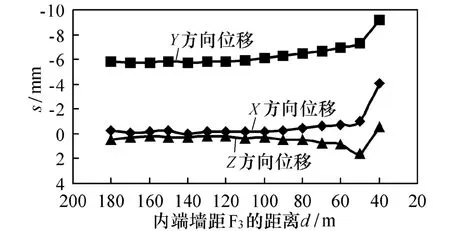
圖8 端墻中心(6#)位移隨端墻距離變化曲線Fig.8 Curve between displacement and distance of 6#

綜合各追蹤點的位移隨內端墻與F3距離的變化特征可看出：雖然不同追蹤部位各個方向位移的變化特點有一定的差異,但總體上主廠房圍巖位移隨內端墻F3距離的減小而不斷增加;特別是在F3距內端墻距離小于60 m后,各個測點的位移總體上呈現出大幅增加的特點,如洞室內端墻中心6#(圖8)。從各個測點的最大位移統計曲線(圖9)也可看出,當距內端墻距離小于60 m后,圍巖的最大位移也產生了較為顯著的變化：可見F3對洞室圍巖變形產生較大影響的距離為60 m。

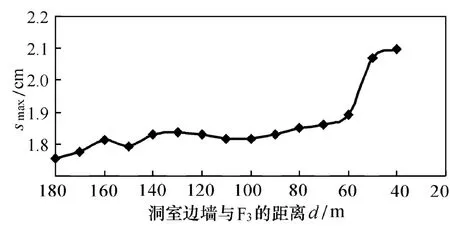
圖9 主廠房圍巖位移最大值隨端墻距離變化曲線Fig.9 Curve between max of displacement and distance

3 Ⅰ-2類結構面對地下洞室群圍巖穩定性的影響

3.1 計算模型及其模擬方案設計

地質模型選擇思路和方法相同,仍以糯扎渡地下廠房為原型,結構面選取較為典型的。廠房區巖體主要為塊狀、次塊狀的花崗巖,總體上為Ⅱ類巖體,假設從主廠房中部通過。

模型的計算參數見表2。為了研究洞室圍巖應力和變形與結構面產狀的相互關系,本次模擬共建立36個模型。結構面與洞室軸線的夾角分別為 15°,30°,45°,60°,75°,90°;其對應的結構面傾角分別為 15°,30°,45°,60°,75°,90°,相互組合構成36個計算模型。在分析過程中,沿軸線每隔10 m記錄模型開挖后追蹤點的位移和應力值,然后進行對比分析。

3.2 計算結果分析

3.2.1 應力場分布特征

地下洞室開挖后,圍巖的應力場發生變化,最大主應力方向與邊墻基本平行,最小主應力與邊墻近于垂直,在斷層與邊墻相交的位置產生拉張應力集中。同樣,根據記錄值,作出各個追蹤點的應力變化曲線進行對比分析(圖10)。

根據模擬結果得出洞室各追蹤點主應力隨傾角、夾角的變化規律如下：在不同夾角和傾角結構面的影響下,洞室頂拱、底板中點和洞室左右邊墻應力變化特點存在一定的差異;但總體看來,隨著結構面與洞室軸線夾角的變化,最大主應力量值減小,最小主應力呈現小幅波動。隨著結構面傾角和結構面與洞室軸線的夾角的增大,對圍巖的應力影響卻逐漸減弱。中等傾角的結構面對洞室邊墻的圍巖應力影響較小,而低傾角的結構面對洞室的邊墻圍巖應力的影響較大;傾角為15°時,隨著傾角的增加主應力不斷增大,應力差也不斷增大：這種應力條件不利于圍巖的穩定。

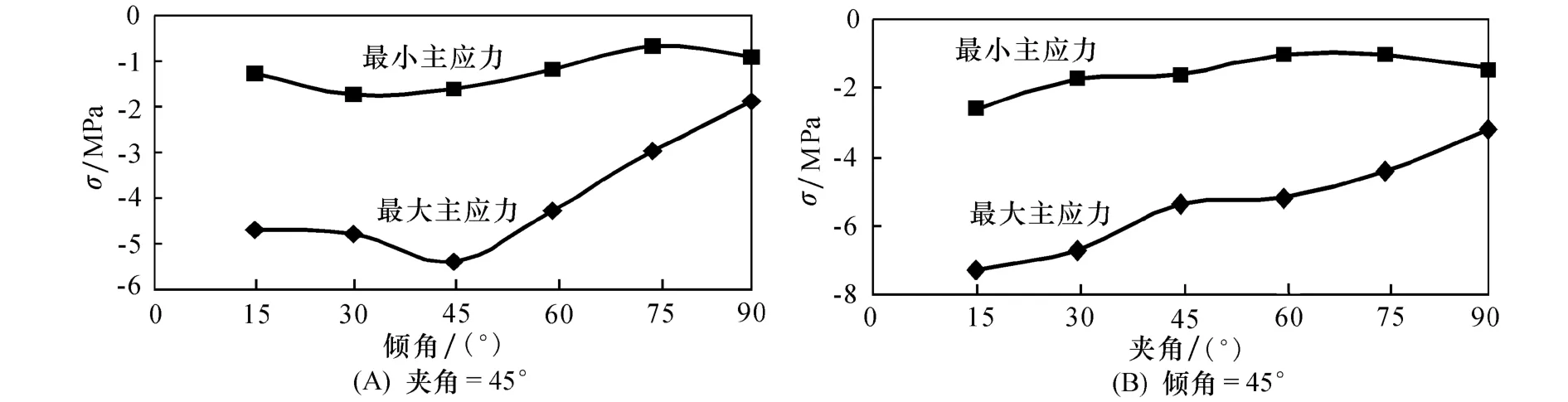
圖10 頂拱追蹤點應力隨傾角(夾角)變化曲線Fig.10 Curve between top tracking point and dip direction or angel

3.2.2 變形場特征

地下洞室開挖后,圍巖在初始應力場的作用下向廠房的臨空面發生了位移,特別在低-中傾角的斷層附近產生了較大的位移。通過開發的程序記錄各個追蹤點的位移,以此作出各個追蹤點的位移變化曲線來進行對比分析,如洞室拱頂位移隨軸線交角的增加和結構面傾角的變化曲線(圖11)。

根據模擬結果得出洞室各追蹤點位移隨傾角、夾角的變化規律如下：隨著結構面產狀的變化,結構面對圍巖位移的影響效果不顯著,得到的位移隨角度的變化曲線雖有一定的規律,但整個量值變化不大,洞室拱頂和底板圍巖主要以向洞室內部回彈變形為主,隨著洞室結構面產狀的變化,量值變化不大;洞室邊墻的圍巖變形主要以X和Y方向的位移為主,特別在中等傾角的情況下,X和Y方向的位移均有所增加,而且總的最大位移量可能成倍增加。可見中等傾角的結構面對圍巖的穩定不利。

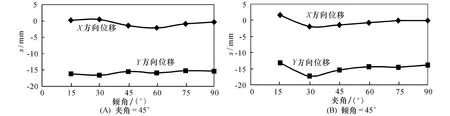
圖11 頂拱追蹤點位移隨傾角、夾角變化曲線Fig.11 Curve between top tracking point and dip direction or angel

4 結論

以糯扎渡地下洞室群為原型,利用數值模擬方法,研究Ⅰ-1級(,)結構面對地下洞室群布置的控制作用和Ⅰ-2類結構面()對地下廠房圍巖應力、變形的影響效應,得出如下基本結論：

a.Ⅰ級結構面與洞室內端墻距離小于80 m時,應力影響效果顯著,最大主應力增大近2倍,而最小主應力減小,使得應力差增大,影響圍巖穩定。當距離大于80 m時,影響效應不明顯。可見,對圍巖應力產生顯著影響主要在80 m以內。

b.主廠房圍巖位移隨內端墻距F3的距離減小而不斷增加,特別是小于60 m后,各點位移增幅達1.5倍;而當距離大于60 m時,影響較小。可見,對圍巖變形產生顯著影響主要在60 m以內。

c.在洞室拱頂和底板處,隨著結構面傾角和結構面與洞室軸線的夾角增大,對圍巖的應力影響逐漸減弱。中等傾角的結構面對洞室邊墻的圍巖應力影響較小,而低傾角的結構面對洞室的邊墻圍巖應力的影響較大。當傾角為15°時,應力差較大,不利于圍巖的穩定。

d.隨著結構面產狀的變化,對圍巖位移的影響不顯著。洞室拱頂和底板圍巖主要以向洞室內部回彈變形為主,洞室邊墻圍巖的變形主要以X和Y方向為主。在中等傾角的情況下,X和Y方向的位移較大。可見中等傾角的結構面對圍巖的穩定不利。

e.綜合分析應力和變形的變化規律,在地質條件復雜的區域布置廠房時,端墻與控制性斷層的距離宜大于80 m,亦即距離應大于3倍洞室跨徑。

[1]張倬元,王士天,王蘭生.工程地質分析原理[M].北京：地質出版社,1994.

[2]孫廣忠.巖體結構力學[M].北京：科學出版社,1988.

[3]谷德振.巖體工程地質力學基礎[M].北京：科學出版社,1979.

[4]黃潤秋,許模,陳劍平,等.復雜巖體結構精細描述及其工程應用[M].北京：科學出版社,2004.

[5]朱維申,李曉靜,郭彥雙,等.地下大型硐室群穩定性的系統性研究[J].巖石力學與工程學報,2004,23(10)：1689-1693.

[6]楊為民,陳衛忠,李術才,等.快速拉格朗日法分析巨型地下硐室群穩定性[J].巖土工程學報,2005,27(2)：230-234.

[7]崔銀祥,聶德新,陳強,等.大跨度地下硐室圍巖結構面空間展布的確定性研究[J].成都理工大學學報：自然科學版,2005,32(4)：0351-356.

[8]魏植生,何偉.糯扎渡水電站樞紐區主要工程地質問題研究[J].水力發電,2005,31(5)：26-28.

[9]王文遠,張四和.糯扎渡水電站左岸廠房區地下硐室群圍巖穩定性研究[J].水力發電,2005,31(5)：30-33.

[10]陳祖安,孫仲樂,彭土標,等.中國水力發電工程：工程地質卷[M].北京：中國電力出版社,2000.

[11]張宗亮.糯扎渡水電站工程特點及關鍵技術研究[J].水力發電,2005,31(5)：5-9.

[12]巨能攀.大跨度高邊墻地下硐室群圍巖穩定性評價及支護方案的系統工程地質研究[D].成都：成都理工大學檔案館,2005.