SVR的樹木生長過程建模及其參數優化研究

王 珊，燕 飛

（北京林業大學，北京100083）

隨著計算機技術的發展，虛擬樹木模型技術已經比較成熟，在一定程度上取代了實際樹木在實驗中的應用。樹木模型易于操作，可以在短時間內進行多種實驗，在以后的研究中還會發揮更重要的作用[1]。樹木模型的開發和應用可以促進對樹木生育規律由定性描述向定量分析的轉化過程，為樹木生產決策系統的開發與應用奠定了很好的基礎。筆者對生長因子的生長過程建模，生長因子包括樹木在生長過程中的高低粗細、光合作用、養分分配、葉片生長、干物質積累等。由于樹木生長的年限較長，且短時間內生長因子的生長量變化不明顯，很難實時記錄其整個生長過程。研究中通常以年為單位，定時測量樹木的各生長量，再對數據進行數理分析，建立預測模型，以此來模擬樹木生命周期的整個生長過程。以樹高為例，對樹木生長過程中樹高的變化進行建模。此建模方法可以推廣到樹木其它生長因子的建模應用中。

1 樹木生長過程建模

在樹木的整個生長過程中，各生長因子總生長量隨年齡的生長變化規律表現為非線性關系，并呈現“S”型曲線。通常將這種關系用數學方式表達出來，便是生長方程[1]。常見的生長方程模型有Logistic模型、Gompertz模型、Richards模型以及Weibull模型等。具體到一組實測的調查因子生長量數據，選擇合適的模型相當重要。各種模型都具有一些共同的性質，比如單調性、漸近性和拐點性質。但是由于各種模型表達式和參數的差異，模型曲線在具體表現形態上又有各自不同的特征。因此針對不同的生長過程，選擇合適的模型才能充分反映研究對象的真實狀況。

2 ε-支持向量回歸機

支持向量回歸機（SVR）就是通過用核函數定義的非線性變換將輸入空間變換到高維空間，并在該高維空間求取回歸函數的學習過程[3-4]。

給定訓練集，其中 xi∈ x=Rn，yi∈y=R，i=1,…,m。ε-不敏感損失函數定義為：

其中ε為不敏感系數，并且ε＞0。

選擇適當的ε，ε-支持向量回歸機的原始優化問題為：

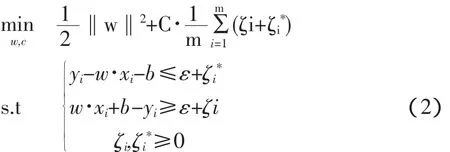
其中C為事先選定的懲罰參數。

在支持向量機中，需要將訓練集從輸入空間映射到另外一個空間。選擇適當的核函數，且滿足

建立Lagrange方程如下：

得到對偶優化問題

另外，制備對照藥材標準品時，因工作程序的原因，粉碎后的樣品距離分裝有一段時間。因此，要嚴格控制粉碎后對照藥材貯藏環境的濕度，確保粉碎后的樣品能保持在一個較低的濕度范圍，減少環境因素對其水分的影響，易于后續的分裝工作。

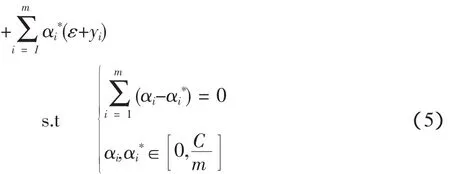
解上述問題可得最優解

構造決策函數為：

3 基于SVR的樹木高度生長模型

根據以上介紹，對樹木生長因子的生長過采用支持向量回歸的方法，建立優化問題；用遺傳算法的方法對支持向量回歸模型的參數進行尋優，找到最佳參數；將最佳參數代入優化問題，并求解，便得到樹木生長因子的模型。具體步驟如下：

3.1 訓練數據來源

由于樹木生長周期長且變化慢，生長數據的采集存在一定的困難，論文中選取樹高作為研究數據。經查閱資料得某樹種1～140年平均樹高的變化[1]。將其進行描點得如下曲線：

圖1 樹高生長曲線

圖中橫坐標為年份，單位為a，縱坐標為高度，單位是m。對此140組數據組成的訓練集進行分析，用支持向量回歸的方法進行處理，建立其樹高生長的數學模型。

3.2 核的選取

常用的4種核函數分別是線性核、多項式核、徑向基（RBF）核。通常低維、高維、小樣本、大樣本等情況的數據集核函數首選RBF核函數。RBF核將樣本數據非線性地映射到高維空間，并具有較寬的收斂域。其數學表達式為：

3.3 參數遺傳算法優化選擇

用支持向量機對數據集進行回歸，需要對其參數（懲罰參數 、不敏感系數 、核參數）進行進行初始設置。懲罰參數的取值過小，易出現欠學習現象，取值過大，又會出現過學習現象。不敏感系數取值較小時，預報精度較高，但支持向量的數目較多；取的過大，支持向量數目急劇減少，但會出現欠學習現象。核參數的取值過小時，易出現過學習現象，而的值過大，又會出現欠學習現象。因此，合理選擇設計參數的值，對于保證支持向量機的性能至關重要[5]。

最常用的方法是網格搜索法。依次將3個參數在設定的范圍內以一定的步長進行劃分，假設分別劃分為M、N、L個，對它們的所有組合分別訓練不同的支持向量機，估計其精度，最終選出學習精度最高的一組作為支持向量回歸的參數。這種方法的缺點就是計算量大，尤其是訓練大樣本數據時搜索工作量太大，費時較多。

遺傳算法具有很好的全局搜索能力，為了解決支持向量機參數選擇的困難，論文中選用遺傳算法，將支持向量機的三個參數作為遺傳算法的個體，經過繁殖、交叉、變異進行搜索，找到最佳參數[6]。算法的步驟如下：（1）選取適應度函數。將遺傳算法每一代的個體作為支持向量機的參數對訓練集進行訓練并預測。對預測結果與原數據進行比較，均方誤差為：

其中f(xi)為訓練集的實際值，yi為預測值，m為訓練集樣本個數。將此均方誤差作為適應度函數，MSE越小說明個體的適應度越高，在遺傳過程中被保留的幾率更大。（2）創建初始種群。采用二進編碼。變量數目為3，種群中的個體數目為100，最大遺傳代數為100。選定三個參數的取值范圍分別為：C∈[0,600]，ε∈[0,4]，y∈[0,0.02]。在此范圍之內隨機建立個體數目為100的初始種群。（3）根據適應度函數計算每個個體的適應度值。（4）繁殖。設置父代與子代的代溝為0.9，交叉概率選為0.7，變異概率選為0.001。對種群依次進行選擇、交叉、變異三個遺傳算法的基本操作后，生成新的種群。（5）對新的種群進行搜索。重復第（3）、（4）步，計算新種群的個體適應度，繁殖，直到遺傳代數等于最大遺傳代數100或者均方誤差小于設定值并結束計算。此時的結果即為最優解。否則返回第（3）步。

3.4 SVR生長模型

將上述方法取得的最優參數C、ε、γ設置支持向量回歸機，對前面提到的訓練集數據進行訓練，求解對偶優化問題，根據決策方程建立樹木高度生長模型。

4 仿真結果與分析

按照以上所列步驟，依次對支持向量回歸機參數進行遺傳算法尋優，將最優參數代入支持向量機的最優化問題，求解該問題得到樹木高度生長的最佳模型。文中所用算法在MATLAB環境下實現。采用遺傳算法工具箱并編寫程序，對支持向量機的參數進行遺傳操作，尋找最佳參數。支持向量機利用臺灣林智仁編寫的LIBSVM，在MATLAB環境下運行，對其參數進行初始化，執行對訓練集數據的非線性回歸操作[7-8]，得到生長模型決策函數，最后對預測數據集進行預測。仿真結果如下：（1）采用遺傳算法對三個參數進行搜索尋優，當遺傳代數為100時結束循環，采用最后的結果為最優參數，如下：C=511.627 522 46，ε=0.000 035 18，γ=1.402 523 79 。（2）首先選取訓練集中奇數年份的數據作為訓練數據。將上述三個參數代入支持向量回歸機中，對選取的訓練集數據進行訓練。得：

并得到70個支持向量，由此便可得出最終的決策函數。

利用此數學模型對訓練集中偶數年份的訓練數據進行預測，得到預測結果均方誤差和相關系數平方，如表1所示。

表1 預測結果與原始數據比較

表中列舉采用支持向量回歸和三種生長方程模型回歸四種不同方法對訓練集數據進行回歸預測的結果比較。可以看出采用支持向量機建立模型的預測結果誤差非常小，幾乎接近于零，預測結果與原始數據的相關系數平方約等于1，也說明預測結果與原始數據的相似程度非常高。而采用三種不同生長方程對生長的非線性過程進行擬合，其結果各不相同，并且均方誤差相對于支持向量機來說大得多，相關系數平方與支持向量機相比也相差很大。通過對比發現，用支持向量機來建立樹木生長模型是精確的。

5 結論

針對樹木生長過程這一非線性過程，采用支持向量回歸對其高度生長過程建模，同時采用遺傳算法對該支持向量回歸機的初始參數進行優化選擇，最后對所得生長模型進行預測與檢驗。從實驗結果可以看出，實驗結果基本準確地反映了樹木高度的生長動態過程，并可以有效地預測未知年份的生長情況。利用支持向量回歸方法建立樹木生長的模型是可行并有效的。該生長過程建模方法可以應用于樹木生長可視化模型的構建、對樹木生理的研究等其它領域，在后續的研究中可以將樹木生長過程中的樹干直徑、陽光等因素添加到模型中。

[1] 孟憲宇.測樹學[M].北京：中國林業出版社，2006.171-201.

[2] 陳金鳳.支持向量機回歸算法的研究與應用[D].無錫：江南大學，2008.11-15.

[3] 李國正，王 猛.支持向量機導論[M].北京：電子工業出版社，2004.98-105.

[4] 鄧乃揚，田英杰.數據挖掘中的新方法—支持向量機[M].北京：科學出版社，2004.224-257.

[5] 李良敏，溫廣瑞，王生昌.基于遺傳算法的回歸型支持向量機參數選擇法[J].計算機工程與應用，2008，44(7)：23-26.

[6] 王小平，曹立明.遺傳算法 [M].西安：西安交通大學出版社，2002.

[7] Chih-Chung Chang and Chih-Jen Lin.LIBSVM：a Library for Support Vector Machines [EB/OL].http：//www.csie.ntu.edu.tw/～cjlin/papers/libsvm.pdf，2009-05-27.

[8] Chih-Wei Hsu，Chih-Chung Chang，Chih-Jen Lin.A Practical Guide to Support Vector Classification [EB/OL]http：//www.csie.ntu.edu.tw/～cjlin/papers/guide/guide.pdf，2009-05-19.