三體船操縱特性計算機數值仿真

盧曉平 姚 迪 王 中

1海軍工程大學 船舶與動力學院，湖北 武漢 430033

2大連船舶重工有限責任公司軍事代表室，遼寧 大連 116000

三體船操縱特性計算機數值仿真

盧曉平1姚 迪2王 中1

1海軍工程大學 船舶與動力學院，湖北 武漢 430033

2大連船舶重工有限責任公司軍事代表室，遼寧 大連 116000

以三體船水動力型和K、T響應型（線性和弱非線性）操縱性運動方程為理論基礎，以三體船重心運動軌跡微分方程組為數值仿真基礎，采用仿真計算工具Matlab軟件，對三體船回轉運動軌跡、操縱性曲線以及Z型操縱試驗曲線等操縱運動特性諸元進行了仿真計算。通過和單體船的對比分析，所得出的計算結果比較合理，計算結果顯示三體船較單體船定常回轉特性有所下降，而直線穩定性有所加強，跟從性和轉首性有所提高。

Hess-Smith法；細長體理論；切片法；操縱性；三體船

1 引 言

三體船型具有良好的耐波性和穩性，同時，在一定速度區間，擁有阻力性能好以及甲板面寬敞等優點。澳大利亞在2005年建造完成了世界最大全鋁質車—客—貨運三體船，船長約127 m，500 t裝載下可達航速40 kn。2008年，美國建造完成三體瀕海戰艦“獨立”號，其航速達到45 kn。這兩艘大型三體船建造完成，標志著國外當代三體船即將進入商業應用和軍事應用時期。三體船水動力研究也得到較為廣泛地開展［1］，而三體船操縱性的研究則十分薄弱。文獻［2］對三體護衛艦一個方案設計的操縱性略有涉及，給出了三體船與單體船回轉性能對比的初步結果。意大利船舶研究中心（CETENA）對常規單體運輸船舶操縱性模擬程序SIMUP進行適當修改后，應用于三體船操縱性能的預報，計算了不同側體布局的三體船的回轉運動和Z形運動，考察了不同側體縱向位置對三體船航向穩定性和回轉性能的影響［3］。中國在三體船操縱性方面的研究，主要包括操縱性水動力導數的經驗公式推廣應用、水動力導數的理論計算、三體船操縱特性數值仿真初步研究［4-5］等。除此之外，三體船的操縱性研究的文獻就鮮有報道。作為新型高性能船型的一種重要航海性能，有必要進一步深入開展三體船的操縱性研究。

本文基于文獻［4，5］研究，以三體船水動力型和線性、弱非線性K、T響應型操縱性運動微分方程為數學模型，以三體船重心運動軌跡微分方程組為數值仿真基礎，采用仿真計算工具——Matl a b軟件，對三體船回轉運動軌跡、操縱性曲線以及Z型操縱試驗曲線等操縱運動特性諸元進行了數值仿真，并據數值仿真結果對三體船的操縱特性進行了分析。

2 數學模型

2.1 坐標系

為了建立艦船操縱運動方程式，采用如圖1所示的兩個右手直角坐標系，其中O0x0y0z0為固定坐標系，Gxyz為隨船坐標系。Gxyz原點取在主船體水線面對稱線的中點（船中處），并假設該點與重心G重合。在艦船操縱性水動力導數計算中，通常采用如圖1所示的隨船坐標系中的運動方程，而在艦船運動軌跡仿真計算中，需要用到固定坐標系O0x0y0z0。

圖1 描述三體船運動的坐標系

2.2 操縱運動方程

基于操縱性MMG分離模型，通過O0x0y0z0與Gxyz坐標變換關系以及近似處理，可以得到隨船坐標系下的艦船操縱運動線性化方程，如式（1）所示：

在工程實用中，往往更關注艏向角φ及其角速度r隨時間變化的規律。對于一般的船舶，由于操舵速度是有限的，且船舶本身的慣性很大，對舵的響應基本是一種緩慢運動，在操舵不是很頻繁的情況下，由線性化的水動力模型可以導出關于r的一階方程：

式（2）也稱為“野本”（Nomoto）方程，式中：

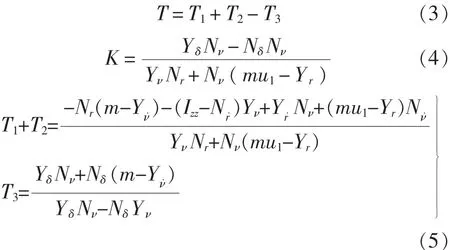
與野本（Nomoto）方程相對應的二階線性響應模型［6］為：

該方程可以在“線性平均”的意義上用于描述中等幅度的操縱運動，方程中隱含的流體動力導數不再是ν，r為零時的流體動力曲線的斜率，而是運動狀態為ν，r時，有關動力曲線的斜率。野本提出對式（6）略加修正后得弱非線性二階響應方程［7］，可以寫作：

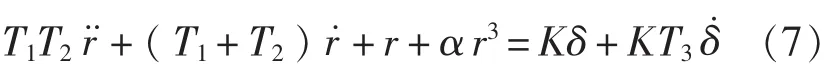
自然，在非線性二階情況下，各種線性流體動力導數將依賴于r變化，非線性影響由αr3體現，α是新引入的常數，而K，T1，T2和T3應由對應于很小的r的線性流體動力導數加以計算。類似于線性化一階KT響應方程，式（7）可以簡化為弱非線性一階KT響應方程，即

式（7）、式（8）中的系數α可通過螺旋試驗結果予以確定，此時式（8）需進一步簡化為定常回轉下相應的表達式：

應用最小二乘法據螺線試驗曲線或水動力數值計算所得r與δ對應關系進行曲線擬合，就可確定 α 或 α 與 K。在式（4）、式（5）中還含有各種操縱 性 水 動 力 導 數 Xu˙、Xu，Yν、Yν˙，Yr、Yr˙，Nν、Nν˙，Nr、Nr˙，Nδ、Yδ等，均為通常含義下的水動力導數，具體含義參見文獻［8］。

以上各種操縱性水動力學方程和響應方程形式的數學模型可直接用于三體船操縱特性預報，也是三體船操縱運動動態特性計算機數值仿真的基礎。三體船操縱性預報與操縱運動計算機仿真并無絕對的分界，只是三體船操縱運動計算機數值仿真強調對三體船操縱運動軌跡、Z型操縱試驗曲線等，具有時域特點的動態過程進行計算機模擬。所以，三體船操縱運動計算機數值仿真的數學模型應在操縱性預報數學模型基礎上，附加求解三體船運動軌跡的微分方程組，或特指求解三體船運動軌跡的微分方程組。

2.3 操縱運動計算機數值仿真模型

如上所述，將三體船計算機數值仿真理解為三體船操縱運動軌跡、Z型操縱試驗曲線以及其他操縱運動參數隨時間變化曲線等，具有時域特點的動態過程計算機數值模擬。此時計算機數值仿真的項目應包括三體船運動軌跡、Z形操縱試驗曲線、速降隨時間變化的曲線等。

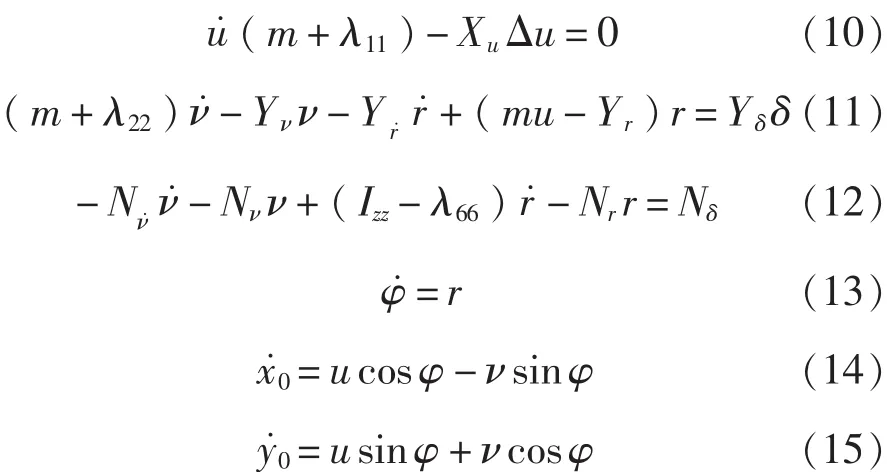
式（10）～式（12）中，λ11、λ22分別為 x、y 軸方向的附加質量，與-Xu˙、-Yν˙相當；λ66為繞 z軸附加慣性矩。聯立求解式（10）～式（15）即可以求出各種舵角下的三體船（重心）運動軌跡。

式（10）是獨立的方程，由此式可以解出u。通常認為在直線航行狀態u的變化不大，近似取為常數；而在定常回轉下u自然也是常數；只是在轉舵初始到定常回轉之間的過渡狀態，u的變化才較為明顯。但回轉中過渡狀態的u即使按式（10）計算也與螺旋槳的工作狀態有關，且不容易準確求出，故在以下對目標船型回轉運動軌跡的數值仿真計算中，據定常回轉下速降公式以及模型試驗資料建立的u近似計算公式，以該近似公式取代式（10）與其他各式聯立求解回轉運動的軌跡。本文采用前蘇聯的費爾索夫提出的定常回轉速降公式：

式中，V0和V分別為直線航行速度和定常回轉速度；R0為定常回轉半徑。

按上式求出V后，進一步給定速降時間和u隨時間變化的函數模態即可得出u的經驗公式。據模型試驗和數值仿真計算資料，本文假設u隨時間變化的函數為以下3次函數：

據文獻［7］給出的幾組速降仿真計算曲線和試驗曲線模態，對一目標船型TR3800確定式（17）的各系數如表1所示。表1中的速降時間需參照回轉運動船體重心軌跡通過迭代計算確定。迭代計算過程如圖2所示。

表1 TR3800船型回轉過程速度變化函數表達式系數

圖2 速降時間計算的一種迭代過程

螺旋試驗曲線（操縱性曲線）盡管不是時域特性曲線，但屬于動態過程曲線，且是描述操縱運動特性的重要資料，本文也將其列入數值仿真的項目。此時按式（8）、式（9）計算確定螺旋試驗曲線。

2.4 三體船的“三體”問題處理

對三體船而言，數學模型中還隱含了對“三體問題”的處理，具體來說“三體問題”的處理隱含在數學模型中出現的水動力導數計算中。本文的處理方法如下：

1）采用三片體分離模型（即MMG模型）的總體思路處理三體問題；

2）由于坐標系原點取在主船體水線面的中點（1／2船長處），故在側體力矩類水動力導數計算中，需要變換坐標（即慣性矩以及力矩移軸定理應用）；

3）片體間存在一定的水動力干擾作用，需對其影響大小進行分析或計入該項影響。

作者所在的課題組研究表明，三體船片體間水動力干擾作用對三體船操縱運動附加質量、附加慣性矩有一定的影響，但影響不大，如圖3～圖5所示。這組圖譜引自課題組對三體船TR3800研究的結果，圖中橫軸、縱軸分別代表 a／L、p／L，即片體縱向偏距、橫向偏距與船長之比；等值線數值表示三體船3種附加質量（附加慣性矩）與相應單片體附加質量（附加慣性矩）之和的比值。將傳統的切片法或細長體理論［9］推廣按MMG思路計算三體船水動力導數不便于計入片體間的水動力干擾，此時可按圖3～圖5這一類三維面元法計算結果對片體間水動力干擾進行修正，或不計片體間水動力干擾。按三維面元法確定水動力導數則可自動計入片體間的水動力干擾作用。

圖 3 TR3800 λ11/（λ011+2λs11）等值線圖譜

圖 4 TR3800 λ22/（λ022+2λs22）等值線圖譜

圖 5 TR3800 λ66/（λ066+2λs66）等值線圖譜

本文在三體船操縱運動計算機數值仿真中，三體船的附加質量、附加慣性矩是按三維面元法計算的，包含有片體間的水動力干擾作用；而速度類導數是采用細長體理論結合切片法計算的，并據有關經驗公式［10］進行了修正，暫未計入片體間的水動力干擾作用。研究表明，如此處理對三體船回轉運動軌跡等仿真項目計算結果影響并不大。計算三體船速度類水動力導數的更好方法應該是計入龍格—庫塔條件和尾渦面的三位面元法，作者及其所在課題組正在進行該項研究。

3 仿真計算實例

3.1 計算船型

取主、側體均為方尾的某三體船型為計算船型（或稱“目標”船型），該船型的主要幾何參數如表2所示。

3.2 回轉運動軌跡仿真

以目標船型TR3800為算例，聯立求解式（11）～式（17），得該船在各種工況下的回轉運動軌跡，圖6～圖13為TR3800三體船及其中體在18 kn、30 kn 兩種航速和 10°、20°兩種舵角下的回轉運動軌跡，這種回轉運動軌跡仿真圖形可用于直觀地分析、比較三體船回轉運動特性。給出TR3800中體回轉運動軌跡是為了將其與TR3800三體船回轉運動軌跡對比，研究側體對于回轉運動的影響。需說明，三體船的中體較常規單體船細長，所以中體的回轉特性還不能夠代表常規單體船的回轉特性。

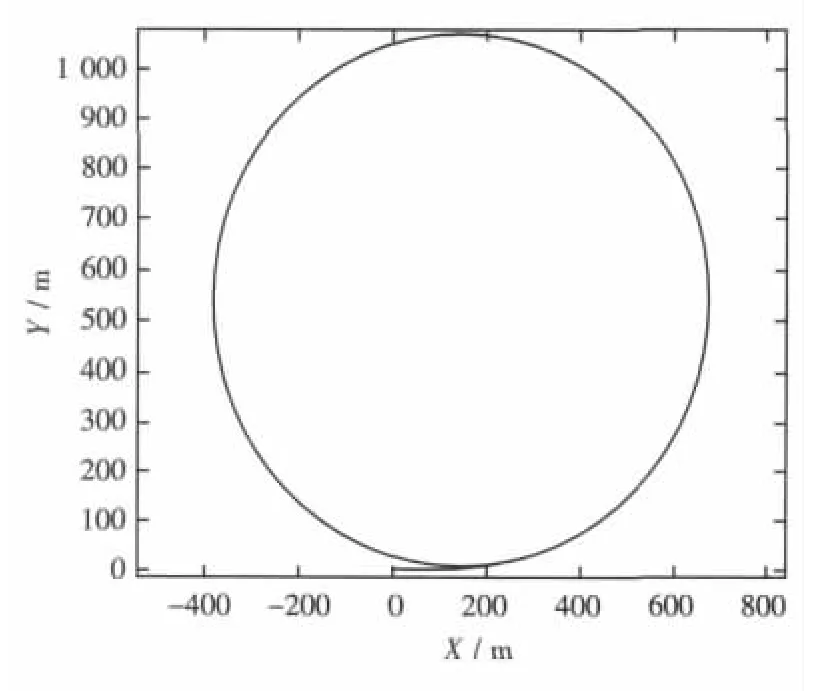
圖6 TR3800船型主體10°、18 kn回轉軌跡

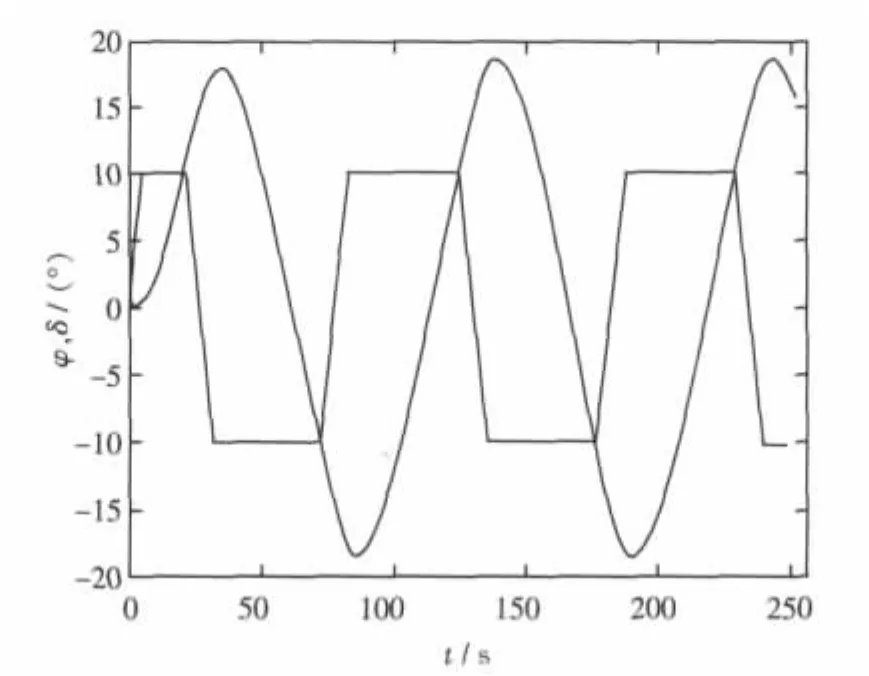
圖7 TR3800船型主體35°、18 kn回轉軌跡

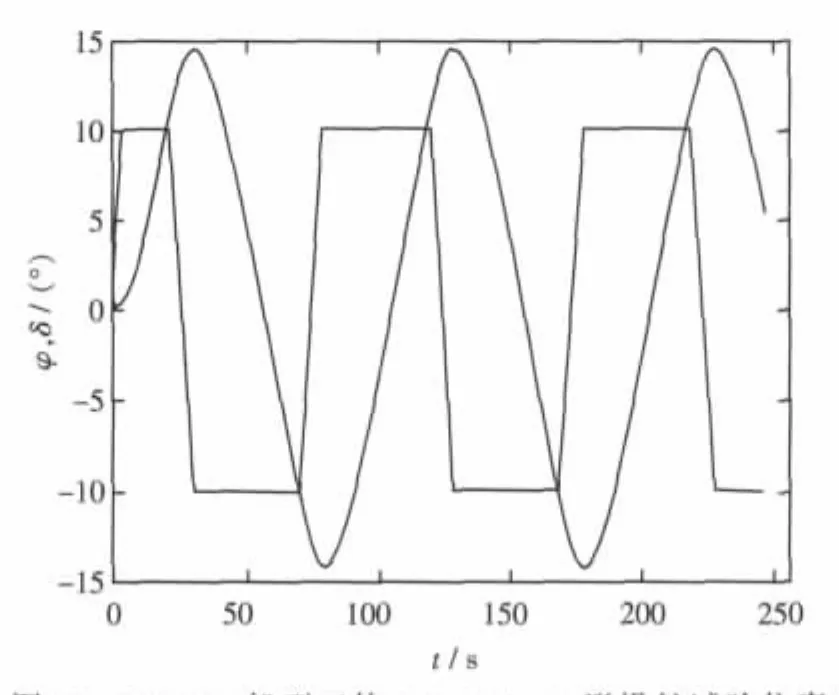
圖8 TR3800船型三體10°、18 kn回轉軌跡

圖9 TR3800船型三體35°、18 kn回轉軌跡

圖10 TR3800船型主體10°、30 kn回轉軌跡

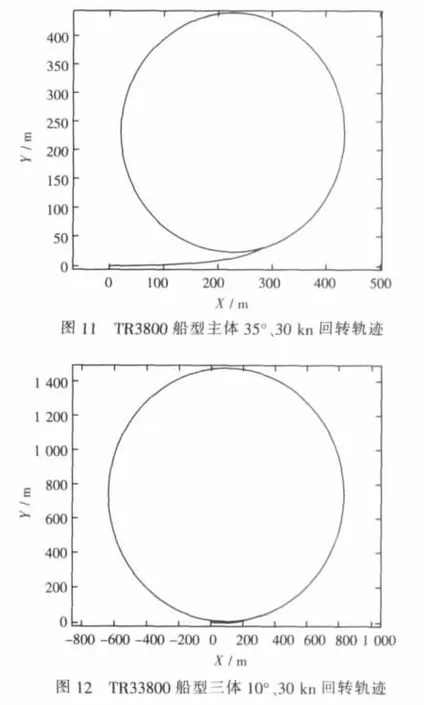
圖13 TR3800船型三體35°、30 kn回轉軌跡

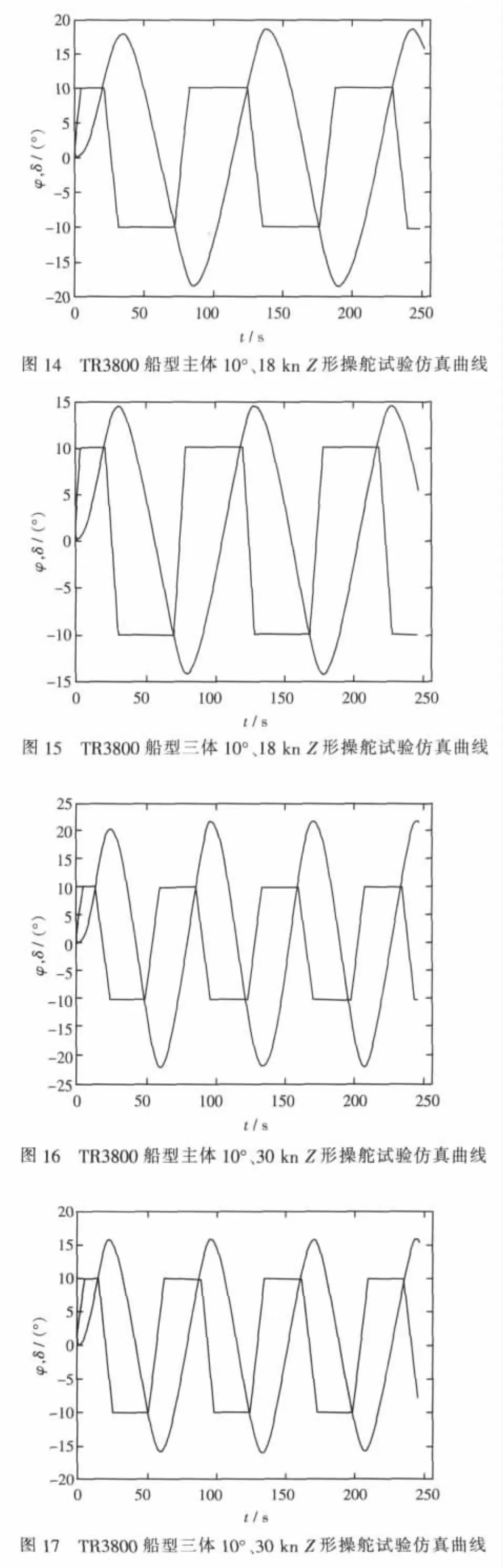
3.3 Z型操縱試驗曲線仿真

仍以目標船型TR3800為算例，按Z形操舵試驗過程，聯立求解式（11）～式（17）各式得該船Z形操舵試驗曲線，如圖14～圖17所示。圖中給出的是 18 kn、30 kn，10°／10°Z 形操舵試驗仿真曲線。該曲線是評定對操舵響應的重要資料，由該圖形可以測算出相應的φOV（超越角）、TL（轉向滯后）、K、T等操縱性指標。

3.4 螺旋試驗曲線仿真

按式（8）、式（9）計算確定目標船型 TR3800主體和三體的18 kn螺旋試驗仿真曲線。如圖18、圖19所示，可用于評估艦船的直線穩定性以及應舵性能。

圖18 TR3800船型18 kn操縱性曲線仿真圖

圖19 TR3800船型18 kn操縱性曲線仿真圖

4 三體船操縱特性分析

據目標三體船操縱特性計算機數值仿真結果為依據，結合船舶操縱性的一般概念和規律，對三體船操縱運動特性進行分析。

4.1 三體船操縱特性與“船舶操縱性標準”對比

表3 船舶操縱性標準

表4 TR3800預報值

4.2 三體船操縱特性分析

在18 kn航速、35°舵角下，對主體（作為單體船）與TR3800三體船操縱特性進行對比分析。二者計算機仿真所得回轉運動軌跡如圖20所示，表5給出了與圖20相對應的更多操縱性指數仿真結果。由圖20所示仿真計算軌跡可直觀地看出三體船的定常回轉特性較單體船略有下降，而三體船的初轉特性較單體船好。軌跡仿真圖形顯示的結果與操縱性各項技術指標仿真結果反映的狀況是一致的。

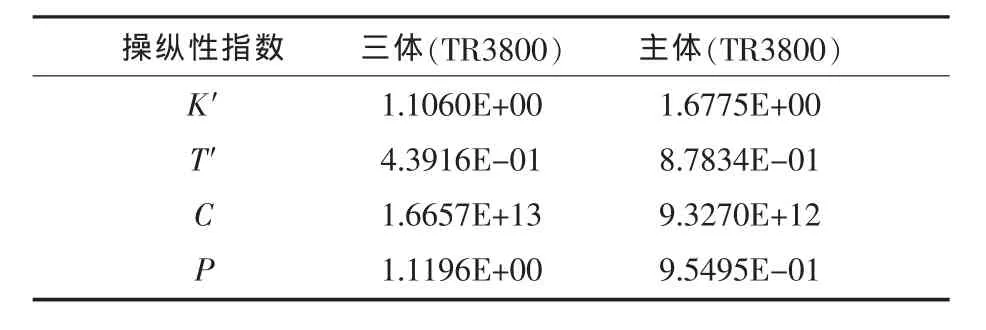
表5 TR3800操縱性指標預報值

據圖20和表5對三體船操縱特性簡要分析如下：

1）回轉性。主體K′值大于相應三體，說明三體船的側體受力狀態不利于定常回轉性能，這與本文得出的仿真圖形顯示的定性規律一致。三體船的回轉性是以定常回轉直徑來衡量的，故得出初步結論是，三體船回轉性較單體船有所下降。

2）航向穩定性。主體T′值明顯大于三體船型，說明側體受力狀態有利于提高直線穩定性，這也與仿真圖形顯示的定性規律一致，故得初步結論為，三體船的直線穩定性能優于單體船。

3）三體船的跟從性和轉首性與單體船相比有所提高。

5 結論

綜上所述，可得如下結論：

1）仿真得出的三體船及其中體操縱特性圖形和指數總體上合理，數值在正常范圍內，本文三體船操縱特性仿真方法具有工程應用前景。

2）三體船定常回轉特性較單體船有所下降，而直線穩定性卻有所加強。

3）三體船的跟從性和轉首性較單體船有所提高。

［1］ 盧曉平，酈云，董祖舜.高速三體船研究進展［J］.海軍工程大學學報，2005（2）：43－48.

［2］ KANG K J，KIM SY，CHOIY R.Seakeeping and maneuvering performances of the 2500 tons class trimaran［C］//IWSH ’2001， Wuhan：Wuhan University of Technology Press，2001.

［3］ LUCA S，ROBERTA D，MICHELE V，et al.Design project of a trimaran multipurpose frigate—study of the hydrodynamic aspects ［C］//Proc.of the 7th International Conference on Fast Sea Transportation FAST 2003，Naples Italy，2003.

［4］ 盧曉平，姚迪，王波.三體船操縱性計算與特性分析［J］.海軍工程大學學報，2009，21（1）：47-53.

［5］ 姚迪.三體船水動力導數計算與操縱特性仿真研究［D］.武漢：海軍工程大學，2008.

［6］ 吳秀恒.船舶操縱性與耐波性［M］.北京：人民交通出版社，1999.

［7］ 賈欣樂，楊鹽生.船舶運動數學模型［M］.大連：大連海事大學出版社，1999.

［8］ 盧曉平.艦船原理［M］.北京：國防工業出版社，2007.

［9］ 吳秀恒，劉祖源，施生達，等.船舶操縱性［M］.北京：國防工業出版社，2005.

［10］盛振邦，劉應中.船舶原理［M］.上海：上海交通大學出版社，2004.

Numerical Simulation of Maneuverability Characteristics of Trimaran

Lu Xiao－ping1 Yao Di2 Wang Zhong1
1 College of Naval Architecture and Power，Naval Univ ersity of Engineering，Wuhan 430033，China
2Military Representative Office in Dalian Ship building Industry Co.Ltd.， Dalian 116000，China

B ased on the theory ofmaneuverability differential equation of hydrodynamic form and K，T responsibility form（both linear and low degree nonlinear equation）， the article took the track motion differential equation of tr i maran gravity center as numerical si mulation foundation，themaneuverability feature of tr i maran including turning tracks，maneuverability curves and zigzagmaneuverability curves were calculated by means of Matlab si mulation software，the calculation results were compared with that of monohull.T he caculated results are reasonable and show that the characteristics of constant turning of the trimaran is less than that ofmonohull， and beeline stability respectively enhanced， follow-up steering and course changing quality improved.

Hess－Smithmethod； slender hull theory； stripmethod； maneuverability； trimaran

U674.951

A

1673－3185（2010）03－01－07

10.3969/j.issn.1673-3185.2010.03.001

2010-01-19

海洋工程國家重點實驗室基金項目（0706）

盧曉平（1957－），男，教授，博士生導師。研究方向：船舶流體力學。E-mail：luxiaoping100@163.com