基于模糊理論的機械多目標優化設計

魏鋒濤， 宋 俐， 李 言， 石 坤， 趙建峰

（西安理工大學機械與精密儀器工程學院，陜西 西安 710048）

WEI Feng-tao, SONG Li, LI Yan, SHI Kun, ZHAO Jian-feng( School of Mechanical and Instrumental Engineering，Xi’an University of Technology , Xi’an Shaanxi 710048，China )

基于模糊理論的機械多目標優化設計

魏鋒濤， 宋 俐， 李 言， 石 坤， 趙建峰

（西安理工大學機械與精密儀器工程學院，陜西 西安 710048）

多目標優化設計各分目標間的矛盾性和不可公度性增加了解決問題的難度，常規求解多目標優化設計方法一般只能求出問題的有效解，而得不到設計的最優結果。該文以蝸桿傳動多目標優化設計為例，采用改進的遺傳算法求得若干有效解后，根據模糊理論中的相似優先比法從中確定出最有效解，即最優解，并可排出它們的優劣順序。

機械設計；多目標優化設計；模糊理論；相似優先比法

工程中常常遇到期望一個設計方案的多項設計指標均達到最優的問題。例如，設計一種機械傳動裝置，希望它的重量最輕、承載能力最高，同時它的性能又最可靠；設計一種高速凸輪機構，不僅要求體積最小，而且還要求其柔性誤差最小，動力學性能最好等。使多于一個設計指標達到最優的問題，就是多目標優化問題。在多目標優化問題中，各分目標之間常常是互相矛盾的，一個分目標值的最優往往會導致另一個或幾個分目標值的最劣。要使幾個分目標同時達到最優，一般來說是非常困難的，有時甚至是不可能的。因此，用常規的方法求解多目標優化問題，得到的是問題的若干個有效解。如何從這些有效解中選擇出最有效解作為最優設計方案，是實際應用必須解決的問題[1]。

文中采用改進遺傳算法求得機械多目標優化問題的理想解和若干有效解，然后根據模糊數學中的相似優先比法確定最有效解，即問題的最優設計方案，并可同時排列出有效解的優劣次序。

1 模糊相似優先比法

應用模糊數學中的相似優先比法[2]確定多目標最優解的基本思想是：首先求出各單目標的最優解，以此構成多目標的理想解；再根據相似優先比法找出各種有效解與理想解的相似（或接近）的程度；與理想解相似（或接近）的程度最高的有效解即為多目標優化的最優解。

1.1 建立相似優先矩陣

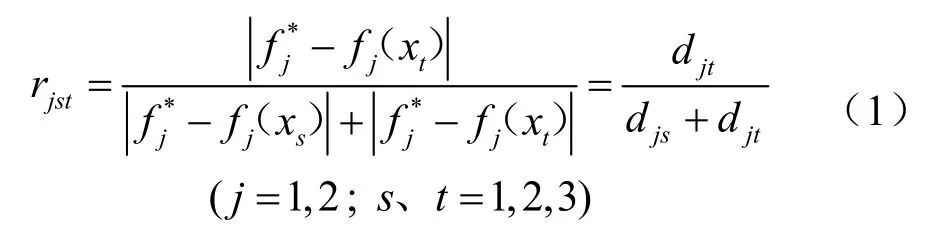
（3） 建立每一個目標的相似優先矩陣 Rj

以相似優先比 rjst為元素組成的矩陣 Rj叫相似優先矩陣，其中

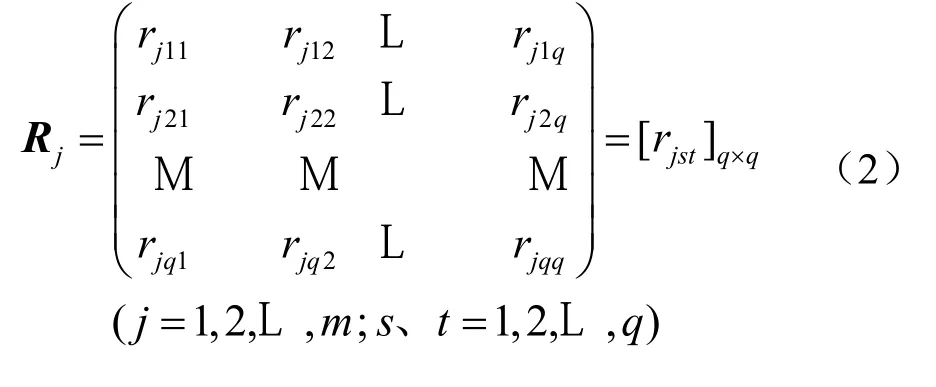
1.2 作 Rj (j= 1,2)的λ截矩陣，確定優先序號和最優解

（3） 確定所有目標的絕對優先序號，得出最優解。對所有 Rj( j =1,2)作完 Njr后，按每行所得的序號 Njr( j = 1 ,2; r = 1 ,2,3)，按行求和，便得所有目標的絕對優先序號 Nr(r = 1 ,2,3)，序號和最小的一個（即min Nr）所對應的有效解便是多目標的最優解。

2 機械多目標優化設計實例及計算過程

2.1 蝸桿傳動多目標優化設計數學模型[3-4]

2.1.1 選擇設計變量

選擇蝸桿頭數 z1、模數m和蝸桿特性系數q為蝸桿傳動的設計變量，即

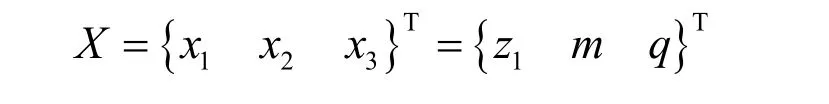
2.1.2 建立目標函數

根據蝸桿傳動的工作特點、結構要求和生產成本，將蝸輪齒冠體積最小、傳動效率最高、中心距最小作為該優化設計的目標函數。

（1） 蝸輪齒冠體積最小

為了降低生產成本，節省較貴重的有色金屬材料，以蝸輪有色合金齒冠體積最小為優化設計的目標函數之一，即

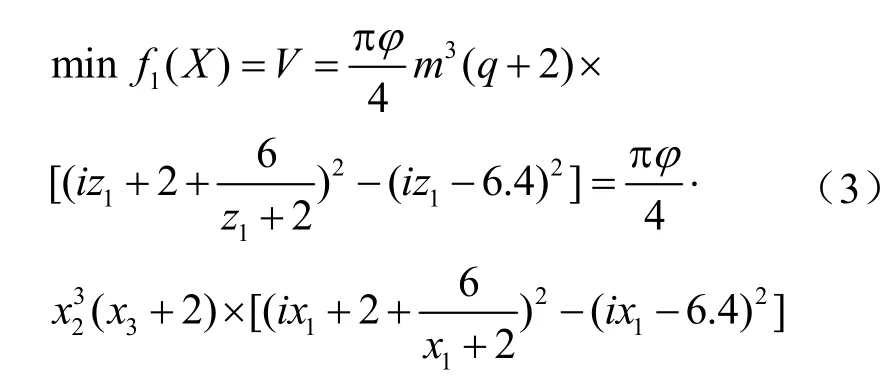
式中 i為傳動比；m為模數；q為蝸桿特性系數；當蝸桿頭數 z1= 1 或 z1= 2 時， φ = 0 .75；當蝸桿頭數 z1= 3 或 z1= 4 時， φ = 0 .67。

（2） 蝸桿傳動效率最高

分析蝸桿傳動的工作情況可知，其總效率主要取決于嚙合摩擦損耗效率η1，而嚙合面間的相對滑動速度 vs則對η1影響很大，成反比關系。為了提高蝸桿傳動效率，就應減小相對滑動速度 vs，即

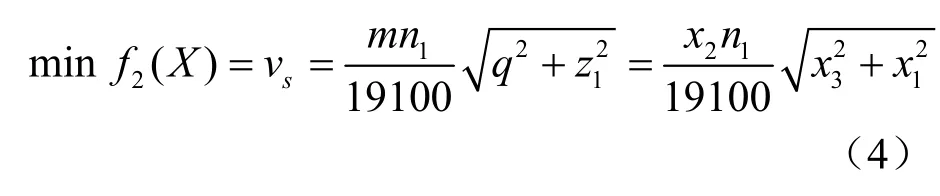
式中 n1為蝸桿轉速。

（3） 中心距最小

為了使蝸桿傳動結構更湊緊，在滿足使用要求的前提下，應使中心距趨于最小，即

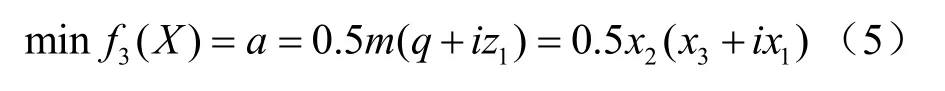
2.1.3 確定約束條件

蝸桿傳動的優化設計應滿足下列限制條件：

（1） 蝸桿頭數 z1的限制

對于動力傳動，一般取 z1= 2 ～4，即

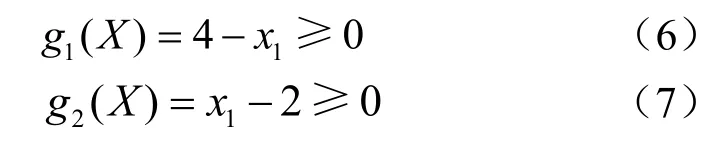
（2） 蝸輪齒數 z2的限制

常取 z2= i z1= 3 0～80，即

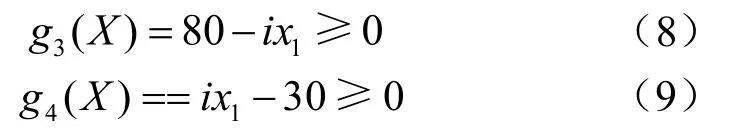
（3） 模數m的限制

常取2 ≤ m ≤ 1 8，即

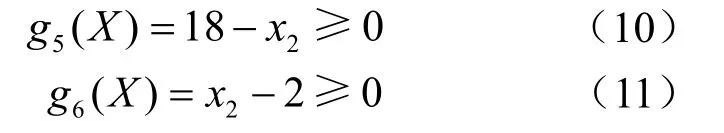
（4） 蝸桿特性系數q的限制

常取 8 ≤ q ≤ 1 6，即

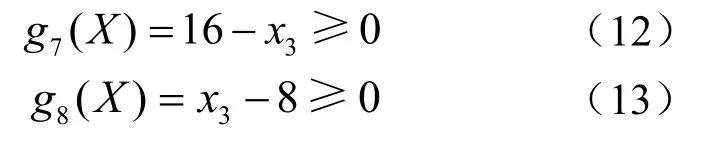
（5） 蝸輪齒面接觸強度的限制

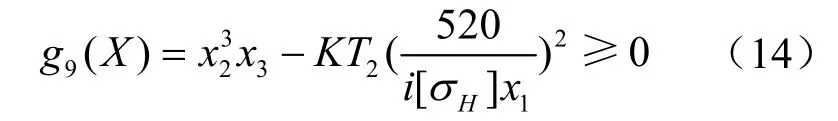
式中 K為載荷系數。

（6） 蝸輪齒根彎曲強度的限制

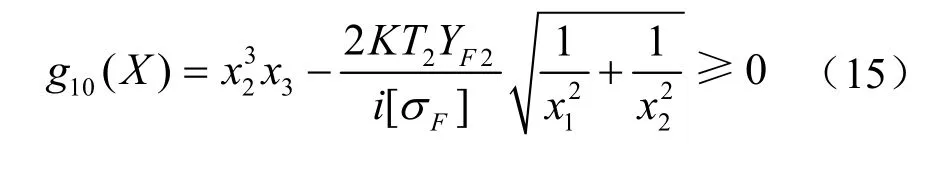
式中 YF2為齒形系數；K為載荷系數。

（7） 蝸桿剛度的限制

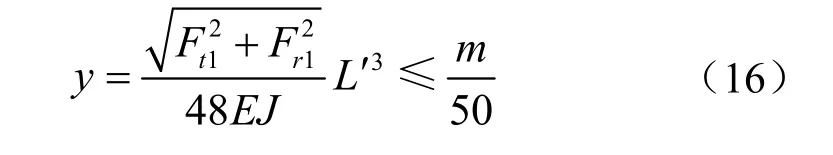
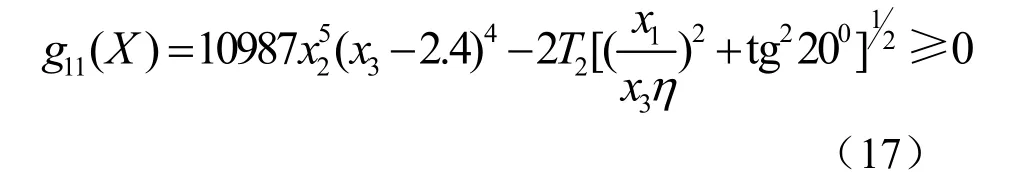
2.1.4 數學模型

綜上所述，蝸桿傳動多目標優化設計的數學模型表示為

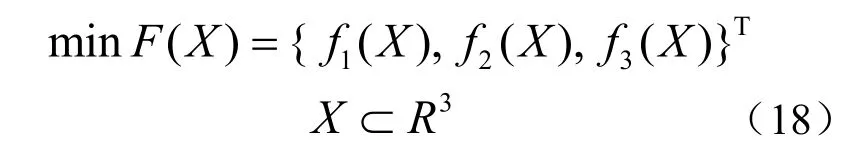
s.t. gi(X ) ≥ 0 (i = 1 ,2,L ,11)

2.2 設計實例

某減速器中的蝸桿傳動，輸入功率 P = 1 0kW，蝸桿轉速n1= 1 460min，兩班工作，載荷平穩，傳動比 i = 2 0，蝸輪齒冠材料為ZCuSn10P1。最優地設計該蝸桿傳動，使蝸桿傳動在滿足承載能力及強度要求條件下，蝸輪齒冠體積最小、傳動效率最高和中心距最小。

2.2.1 優化設計問題的理想解和有效解

文中采用改進遺傳算法求解得到該優化問題的理想解和有效解。該算法在標準遺傳算法的基礎上進行了實數編碼策略、聯賽選擇機制及動態調整交叉概率和變異概率引入自適應算子等方面的改進，參數設置為：群體規模 N = 8 0，采用終止代數為200代與連續10代平均目標函數值不大于最小目標函數值的0.001相結合的方法來判斷是否結束程序運行[5-7]。

（1） 理想解

用改進遺傳算法分別求出該問題中各單目標函數的最優解，即理想解及相應的函數值為

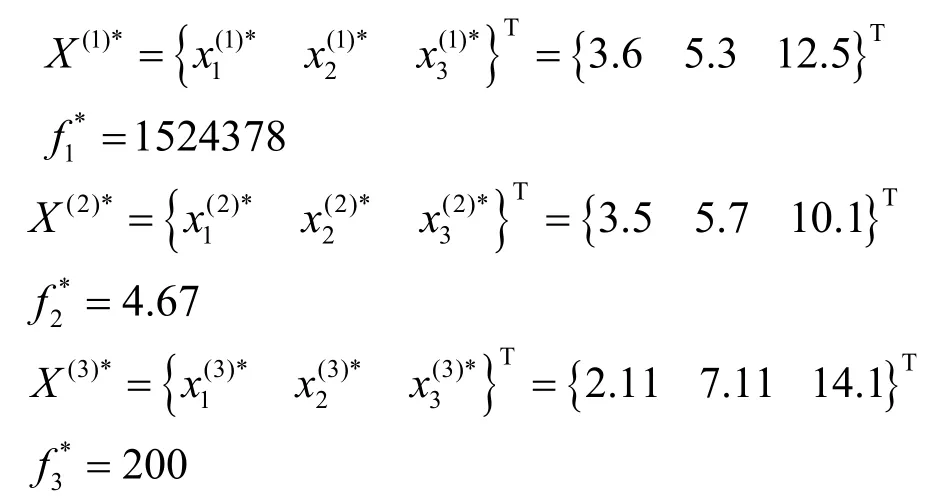
（2） 有效解

用改進遺傳算法分別根據理想點法、線性加權法和平方加權法三種多目標優化問題的處理方法進行求解得到三組有效解

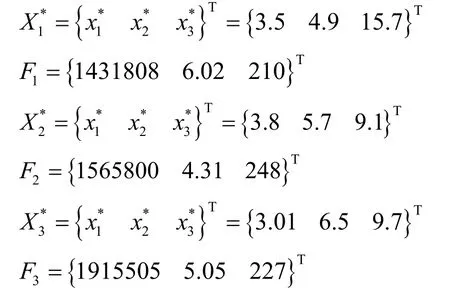
2.2.2 用模糊相似優先比法求最有效解

（1） 建立相似優先矩陣

該優化問題有3個目標和3個有效解，即可得到3個相似優先矩陣

（2） 作λ截矩陣，確定優先序號和最優解

各 有 效 解 的 優 先 序 號 Njr( j =1,2; r= 1 ,2,3)和序號 Nr(r = 1 ,2,3)如表 1所示。

表1 有效解的行序號和絕對優先序號

由表1知，序號和最小的有效解是 F2。因此，F2是該多目標優化問題的最有效解，即其次為F1、 F3。

與常規設計方案（ Z1= 2 , m = 9 , q = 1 0）比較，蝸輪齒冠體積減少了33.8%，傳動效率提高了26.1%、傳動中心距減少了6.7%。可見，采用多目標優化設計方法進行設計，得到了比傳統設計更為合理的結構設計方案，使蝸輪和蝸桿傳動在滿足承載能力及強度要求的條件下，蝸輪齒冠體積最小、傳動效率最高、中心距最小，從而使整體設計結構更為緊湊。與蝸桿傳動的單目標設計相比，運用多目標優化方法使蝸桿傳動設計得到了整體最優的設計方案，結果合理、符合工程實際。

3 結 論

本文利用改進遺傳算法對機械多目標優化設計問題的理想解和有效解進行了求解，并根據模糊數學中的相似優先比法，從若干個有效解中選擇出最有效解并排列出它們的優劣次序。整個求解過程表明，這種方法大大降低了人為因素對解決此類優化問題的影響，使最終得到的優化結果更科學、更符合實際情況。由于這種多目標優化問題的處理方法不受目標函數個數的限制，因此隨著目標函數個數的增加且有效解的個數增多時，更能顯出該方法的優越性。

[1] 劉惟信. 機械最優化設計[M]. 北京: 清華大學出版社, 1994. 230-236.

[2] 王彩華, 宋連天. 模糊論方法學[M]. 北京: 中國建筑工業出版社, 1988. 304-309.

[3] 濮良貴, 紀名剛. 機械設計[M]. 北京: 高等教育出版社, 2001. 239-259.

[4] 王文博. 機構和機械零部件優化設計[M]. 北京: 機械工業出版社, 1990. 240-244.

[5] 王小平, 曹立顯. 遺傳算法——理論、應用與軟件實現[M]. 西安: 西安交通大學出版社, 2002. 73-74.

[6] 崔艷梅, 王麗萍, 等. 基于遺傳算法的四桿機構的優化設計[J]. 機械傳動, 2004, 28(4): 22-24.

[7] 李 斌, 朱如鵬. 基于遺傳算法的行星齒輪傳動優化及 MATLAB實現[J]. 機械設計, 2004, 21(10): 29-31.

Mechanical Multi-Object Optimization Design Based on Fuzzy Theory

It is difficult to solve multi-objective optimization for inconsistency and incomparability among each single object. Multi-objective mathematical model of worm transmission is established. Effective solutions are obtained by general optimal arithmetic, such as improved genetic algorithm. The optimal solution is chosen from these available effective solutions and then ranked by the similarity priority ratio method of fuzzy theory.

machine design; multi-objective optimization design; fuzzy theory; similarity priority ratio method

TH 122

A

1003-0158(2010)02-0009-04

WEI Feng-tao, SONG Li, LI Yan, SHI Kun, ZHAO Jian-feng
( School of Mechanical and Instrumental Engineering，Xi’an University of Technology , Xi’an Shaanxi 710048，China )

2008-09-09

陜西省自然科學基金資助項目（2006E108）；西安理工大學科學研究基金資助項目（102-210710）

魏鋒濤（1976-），男，陜西合陽人，講師，博士研究生，主要研究方向為結構優化設計。