基于小波分析的電機故障診斷研究

蘭州理工大學 電信學院（甘肅 蘭州 730050） 楊新華 來 帥

山西昆明煙草有限責任公司（山西 太原 030012） 張麗娟

0 引言

電機出現故障時，故障信號中往往含有大量的時變、短時突發性質的成分[1]。因此可以通過檢測、分析故障信號，獲得電機的故障信息。傳統的信號分析方法，如傅立葉變換，是一種純頻域分析,缺乏空間局部性,不能滿足對軸承故障信號分析的要求。而小波分析和小波包分析法具有良好的時頻局部性，能夠將信號在任意頻段進行劃分，從而使在不同頻段的各種故障特征信號更加容易被識別和提取[2]。基于小波包分析處理非平穩信號的優越性，本文選用小波包分析對電機故障信號進行分析，并在MATLAB中對分析結果進行了驗證。

1 電機故障類型

電機集電氣與機械部件于一體，故障原因復雜，種類繁雜，征兆呈多樣性，既有機械故障的一般特性，又有電氣部件、磁場等故障特性。大量的故障結果分析顯示:軸承類故障占42%,繞組類占40%，絕緣類故障占5%[5]。可見，電機軸承故障是導致電機失效的主要原因之一。因此本文模擬了電機滾動軸承故障，應用小波包分析方法對異步電動機的軸承故障特征進行提取，利用峭度值計算和和小波包分析相結合的方法，確定電機的故障類型。

實驗研究表明，電機振動量是檢測電動機故障的非常好的狀態監測參數，在不影響電動機運行的條件下對其振動信號進行頻譜分析可以檢測多種故障。

2 小波包理論

小波包是在小波概念的基礎上發展延伸的，是小波概念的推廣,它將小波分析沒有細分的高頻部分信號作進一步的分解[2]。

2.1 小波包算法

小波包的定義是在多分辨率分析的基礎上提出來的，而多分辨率分析的實質是將兩個相鄰分辨率之間的信號進行逐級分解。小波包分解的基本思想是:把信號投影到一組互相正交的尺度函數和小波函數構成的子空間上，從而將信號在不同尺度上展開，以便提取信號在不同頻帶的特征，同時也將信號在各個尺度上的時域特征完整的保留下來。

設共軛正交鏡像濾波器系數分別為:hn=h0(n)和 gn=h1(n)；定義一列遞歸函數 U(t)，滿足雙尺度方程：

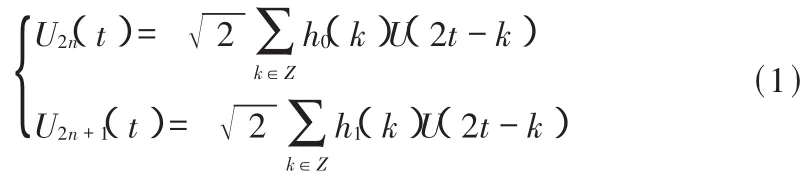
則,函數集合{un(t),n=0,1,2…}是由基函數 u0(t)=φ(t)所確定的小波包。由此，小波包{un(t)}是包括尺度函數 u0(t)和小波函數 u1(t)在內的一個具有一定聯系的函數的集合。

經振動傳感器采集到的故障信號，通過前置濾波、信號調理后送A/D轉化成數字信號，為了能使數字信號在計算機上實現小波包分解，我們設{Sk,k∈N}為離散序列,定義算子

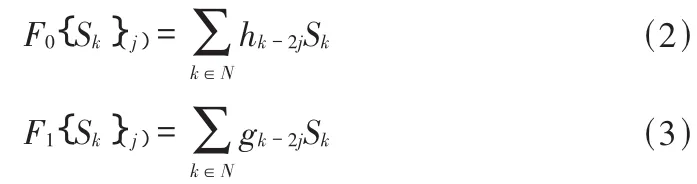
設{fp(00),p∈N}為經過離散的電機故障信號,小波包分解的分解算法為:

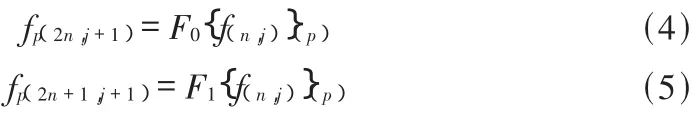
式中:p為小波包分解各序列序列點；j:為小波包分解層數。

為了實現小波包分解，我們將經過離散處理的電機故障信號通過共軛正交鏡像濾波器，這樣，離散故障信號就被分解到各個頻段內。

從上面的分析可以看出，多分辨率分析只是完成了對信號的低頻部分的分解，但并不是一個完整的樹狀結構；為了實現對信號的更加精細的分析，本文選擇小波包分析，它不但能實現對低頻部分的分解，而且也能對信號高頻部分分解，從而構成了一個完整的樹狀結構。

2.2 小波包基的選取

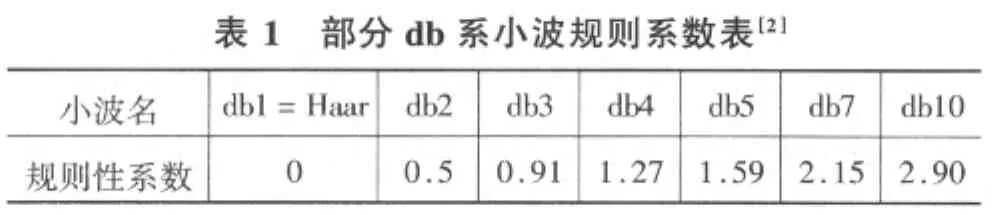
目前，對于小波包基的選取并沒有形成一個統一的標準，在遵循一般性原則的基礎上，要具體問題具體分析。就被檢測信號的特征而言，我們檢測的是電機的故障信號，要從中提取非平穩的瞬時、突變和奇異的成分，也就是說要提取有限頻帶上的信息，所以在選取小波基時，其時頻兩域的緊支撐能力應首先被考慮；而對于信號的奇異性檢測，當信號產生奇異點時，往往在突變處含有高頻成分，而且信號形狀不規則，從規則性系數表可知，規則性系數越大，規則性就越好，但在分析電機故障的振動信號時，我們更加關心它的低頻成分，所以對于dbN的小波函數的消失矩階數不應太高；同時，在選擇小波基的過程中，正則性原則也不容忽視，因為正則性越好，檢測突變點的效果就越不理想，所以在這里我們選擇了正則性不是很好的db3小波[3]。

綜上所述，在電機的機械故障診斷中，為了有效地分析突變信號，在小波包基的選取上，主要滿足定區間的緊支撐和足夠的消失矩階數，這樣能有效的消除噪聲，發現奇異點。

通過以上的分析和比較，我們選擇了db3作為小波基。圖1為db3的尺度函數和小波函數示意圖。

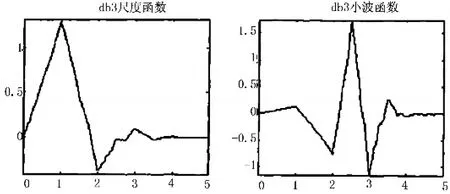
圖1 db3尺度函數與小波函數示意圖

3 小波包故障診斷的實例分析

為了驗證小波包分解算法的正確性和可靠性，采集電流信號和振動信號，利用小波分析的方法獲得故障類型，本文只以振動信號的分析為例，加以闡述。

?

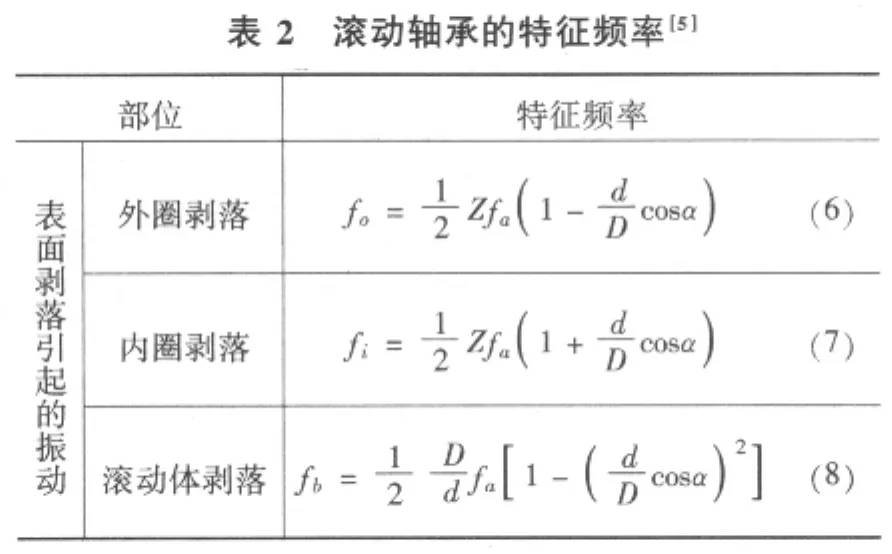
本實例事先對電機的軸承進行處理，在滾動體上人為加工制造一個深約0.5mm，直徑約1.0mm的故障點，用來模擬軸承滾動體故障。滾動軸承參數為:滾動軸承為圓柱滾子軸承，型號為37306，內徑 d=180mm，外徑 D=310mm,z=7,!=0°。將滾動軸承的相關參數帶入滾動軸承特征頻率中，由(6)，(7)，(8)可分別計算得出：外環故障的特征頻率為41.5Hz，內環故障的特征頻率為136.42Hz，滾動體故障的特征頻率為18.9Hz。

?

圖2為軸承滾動體故障時的時域信號，根據峭度系數的計算公式[7]：

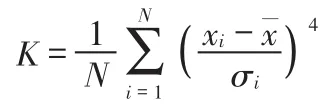
式中,N為采樣長度；"i為標準差；xi為信號值；xˉ為信號均值。

計算可到 K=5.12。電機無故障運轉時，振動信號的幅值分布接近正態分布，峭度值指標 K=3,而本例中 K=5.12，根據峭度值指標判斷，軸承已經出現明顯的故障，但并不能確定其故障類型[7]。

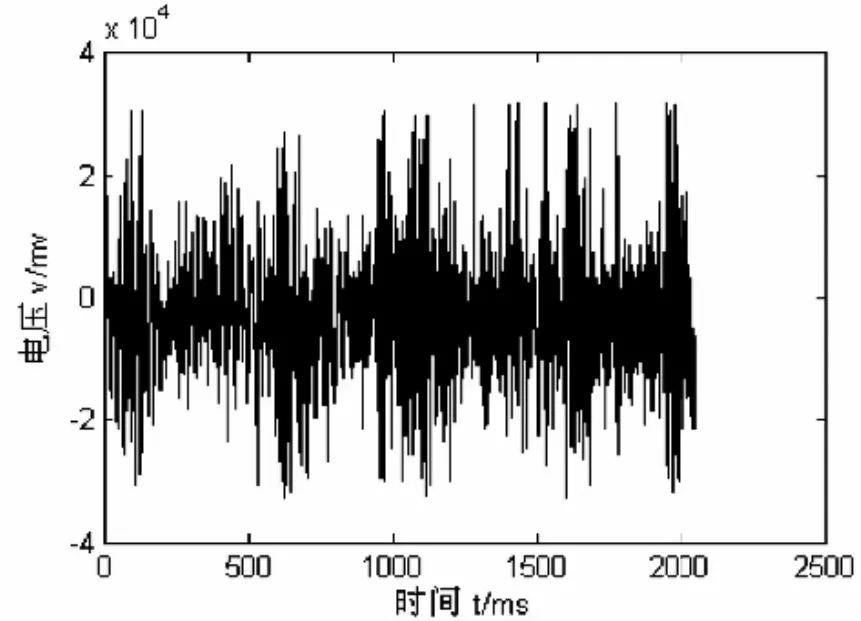
圖2 故障軸承的時域信號

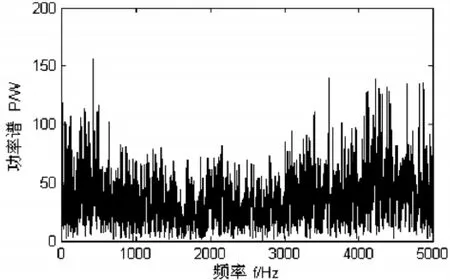
圖3 滾動體故障功率譜圖

圖3為滾動體故障的功率譜圖,然而依據此功率譜圖仍不能清晰的觀察軸承故障的特征頻率，所以同樣不能確定軸承故障類型。

利用db3小波繼續對時域信號進行分析。在本文中我們將信號進行6層小波包分解，這樣信號被分解為64個頻段，頻段帶寬為由上文可知，軸承滾動體故障特征頻率為18.9Hz,在第一頻段范圍內，故而對第六層(6，0)節點的故障特征頻率信號作小波包重構[7]，圖4為節點故障特征頻段重構信號，圖5為其功率譜。

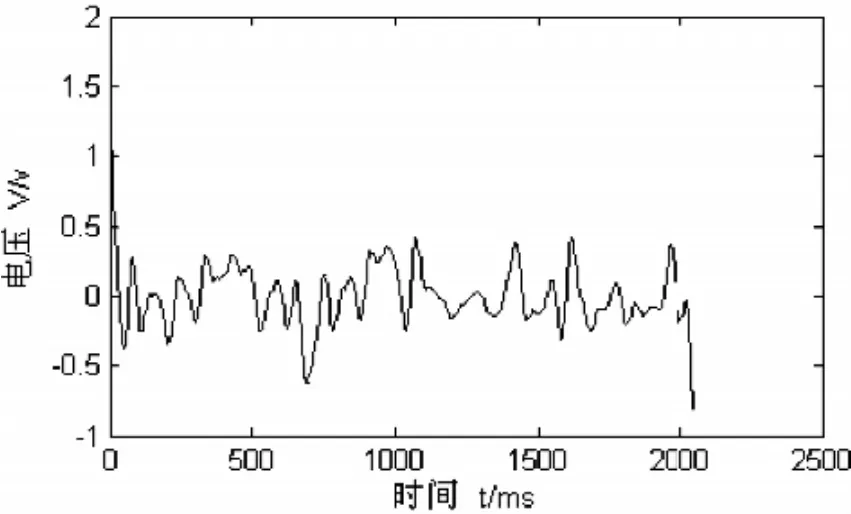
圖4 （6，0）節點故障特征頻段重構信號

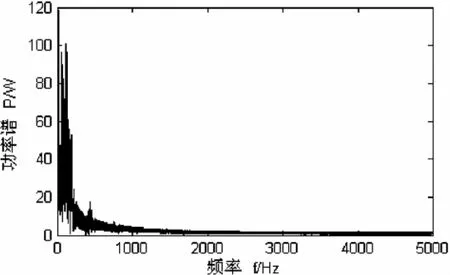
圖5 故障特征頻段重構信號的功率譜

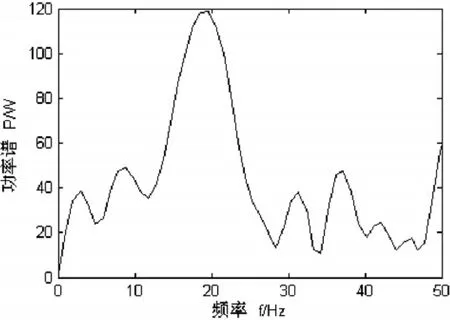
圖6 功率譜局部放大圖

從圖6的功率譜局部放大圖可以清晰發現，在頻率18.9Hz附近能量幅值突然增大，沖擊嚴重，說明軸承確實存在滾動體故障。

4 結論

本文應用小波分析的方法，結合振動信號的峭度值計算，對存在已知軸承故障的電機振動信號進行小波包分解，有效的濾除了干擾信號，實現了信噪分離[8]，從軸承故障特征頻率的數值和能量兩個方面確定了電機的故障類型。仿真結果顯示，實際故障類型與分析所得的故障類型相吻合，說明本文提出的方法有效可行。

[1] Benbouzid,Beguenance,Vieira.Induction motor asymmetrical faults detection using advanced signal processing techniques,IEEE EC,1999,14(2):147～152.

[2] 飛思科技產品研發中心.小波分析理論與MATLAB7實現[M].北京:電子工業出版社,2005

[3] 王芳，魯順昌.基于小波包分析的電機故障檢測[J].電機與控制應用，2008,35(7)

[4] 湯紅誠，李著信.小波變換在故障診斷中應用[J].儀器儀表學報,2003,24(4):407～409

[5] 沈標正.電機故障診斷技術[M].北京：機械工業出版社，1996

[6] 程止興.小波分析算法與應用[M],西安，西安交通大學出版社，1998

[7] 袁云龍，基于小波包分析的滾動軸承故障診斷研究.控制與檢測,2008(7):62～65

[8] 袁云龍,基于峭度小波包分析的滾動軸承故障診斷.新工藝新技術,2008(5):43～46