基于連續(xù)測角的被動測距技術(shù)研究

申波，朱斌，龍波，郭立新

（西南技術(shù)物理研究所四川成都610041）

在偵察定位目標(biāo)過程中，目標(biāo)距離是影響系統(tǒng)安全和武器首發(fā)命中的重要因素，其準確度影響到能否準確避開敵方威脅源的攻擊，并對敵方目標(biāo)進行精確的打擊，所以探測目標(biāo)的距離便成為關(guān)鍵技術(shù)之一。

測距技術(shù)可分為主動和被動測距2種。前者是通過自身發(fā)射大功率信號探測目標(biāo)，通過分析目標(biāo)信息確定目標(biāo)的距離，但是由于主動測距技術(shù)自身需要發(fā)射探測信號，在實戰(zhàn)中不便于隱蔽自己，容易被敵方發(fā)現(xiàn)，而遭受干擾甚至毀滅性打擊。其探測精度較高，但是探測距離卻比較有限；而后者又稱為無源定位技術(shù)，是通過探測目標(biāo)自身的輻射信息、角度信息或其他信息，并對其分析來確定目標(biāo)距離。該技術(shù)不需自身發(fā)射探測信號，從而能夠很好地隱蔽自己，具備極強的生存能力和抗干擾能力，被動測距技術(shù)可省略成本較高的發(fā)射單元，具有較高的性價比。二者相比，被動測距技術(shù)具有更遠的探測能力。

1 系統(tǒng)模型的建立

機載紅外搜索跟蹤系統(tǒng)在發(fā)現(xiàn)并跟蹤上目標(biāo)后，可以連續(xù)獲得目標(biāo)的角度數(shù)據(jù)。在沒有目標(biāo)任何位置信息的情況下，利用這些角度數(shù)據(jù)，通過建立合適的模型，選用合適的濾波算法，就可以有效地估計出目標(biāo)的距離。在空間極坐標(biāo)系中，載機跟蹤運動目標(biāo)時，目標(biāo)的三維運動狀態(tài)如圖1所示。

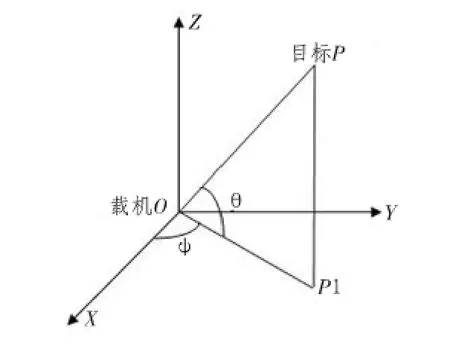
圖1 空間極坐標(biāo)系三維運動示意圖Fig.1 Schematic diagram of three-dimensional motion in the polar coordinates

描述目標(biāo)三維運動的狀態(tài)向量表示如下：

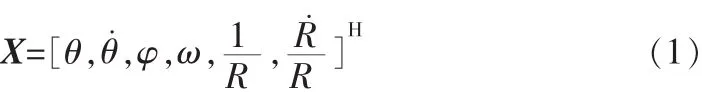
式中，θ和φ分別是目標(biāo)的俯仰角和方位角，其導(dǎo)數(shù)分別為對應(yīng)角速度，ω是方位角速度的分量，R是目標(biāo)與觀測平臺間的相對距離，其導(dǎo)數(shù)為目標(biāo)與觀測平臺間的相對速度。

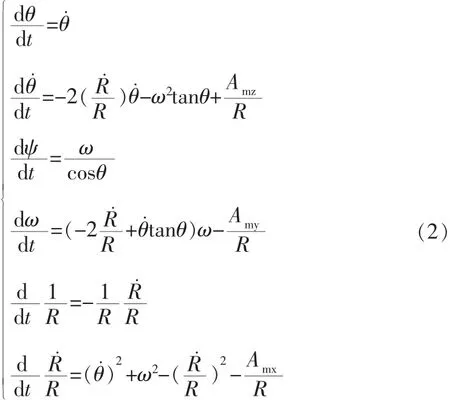
這些狀態(tài)向量滿足以下方程組：式中，Amx，Amy，Amz為觀測平臺本身的加速度，可作為已知量處理[1]。

基于測角的被動測距方法的觀測向量為方位角和俯仰角，即：

可得測量矩陣為

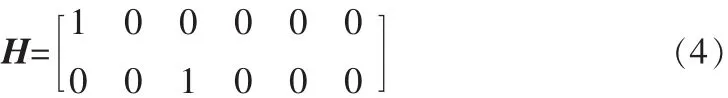
2 可觀測性分析

對于非線性系統(tǒng)的可觀測性，工程研究中常采用Lee和Dum等人提出的可觀測性定理來分析。

定理對于非線性系統(tǒng)，

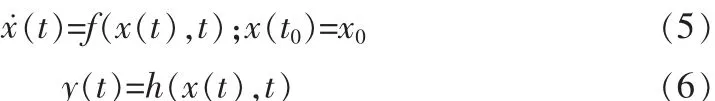
如果對于凸集s∈Rn上的所有x0，都有

是正定的，則系統(tǒng)在s上是完全可觀測的。

上述定理是針對連續(xù)系統(tǒng)的，對于非線性的離散系統(tǒng)，與此可觀測性定理等價的結(jié)論是：對于初始集合s中的n維矢量Xk0，記

如果存在正整數(shù)N使矩陣A（i，i+N-1）的秩滿足：

則系統(tǒng)在s上是完全可觀測的[2]。

在空間極坐標(biāo)系下，設(shè)系統(tǒng)的狀態(tài)變量為

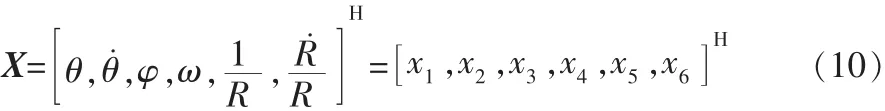
由狀態(tài)向量滿足的狀態(tài)方程式（2），可得

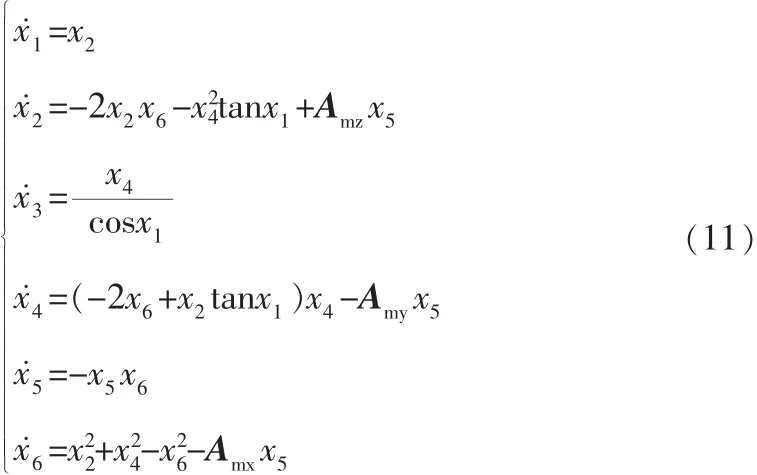
可得狀態(tài)轉(zhuǎn)移矩陣

由于狀態(tài)向量是6×1維向量，而觀測向量是2×1維向量，所以進行N=3次觀測，得到3個觀測矢量，可得

從而可以求出Γ矩陣，并得出其行列式為

如果rankA=6，則根據(jù)前面所述非線性系統(tǒng)的可觀測性定理可知，此時系統(tǒng)是可觀測的。由于矩陣A是6×6方陣，所以rankΓ的充要條件是det A≠0。

由式（14）可以看到觀測平臺加速度分量Amy和Amz如果同時為0，則detA=0，此時系統(tǒng)不可觀測。所以可知要系統(tǒng)是可觀測的，則觀測平臺加速度必定不能為0，即觀測平臺必須作機動，也就可以得出載機作機動是本系統(tǒng)模型可觀測的必要條件。

3 濾波算法

在光電雷達獲取目標(biāo)的角度數(shù)據(jù)之后，需要選取合適的濾波算法來進行濾波估計，而得出目標(biāo)相對載機的距離。基于本系統(tǒng)是非線性系統(tǒng)，故采用非線性濾波算法來進行濾波。常用的非線性濾波算法有：擴展卡爾曼濾波算法（EKF）[3-4]、修正協(xié)方差的擴展卡爾曼濾波算法（MVEKF）[5]，修正增益的擴展卡爾曼濾波算法（MGEKF）[6]和不敏卡爾曼濾波算法（UKF）[7]。

對于非線性濾波問題，通常的處理方法是利用線性化技巧將非線性問題轉(zhuǎn)化為一個近似的線性濾波問題，套用線性濾波理論得到求解原非線性濾波問題的次優(yōu)濾波算法。擴展卡爾曼濾波算法（EKF）是用泰勒級數(shù)將非線性的狀態(tài)方程進行一階或二階展開，對狀態(tài)方程進行線性化。

修正協(xié)方差的擴展卡爾曼濾波（MVEKF），其基本思想是在EKF方法中采用更新的狀態(tài)值X＾（k+1/k+1）重新計算雅克比矩陣，并用此新的雅克比矩陣作為測量矩陣對協(xié)方差矩陣進行更新，從而得到更加準確的修正協(xié)方差矩陣。

修正增益的擴展卡爾曼濾波（MGEKF），其基本思想是在EKF方法中計算更新濾波協(xié)方差矩陣時，用一個修正增益函數(shù)矩陣g（Zk+1，X＾（k+1）/k）來代替量測矩陣Hk+1（X＾（k+1）/k）。這個修正增益函數(shù)矩陣g（Zk+1，X＾（k+1）/k）嚴格滿足以下關(guān)系式：

其優(yōu)點在于用可以減小觀測方程的線性化誤差，提高濾波精度。

不敏卡爾曼濾波（UKF）是用于計算經(jīng)過非線性變換的隨機變量統(tǒng)計的一種新方法。它不需對非線性狀態(tài)和測量模型進行線性化，而是對狀態(tài)變量的后驗概率密度函數(shù)（PDF）進行近似化，進行不敏變換（UT變換），表現(xiàn)為一系列選取好的采樣點，這些采樣點完全體現(xiàn)了高斯密度的真實均值和協(xié)方差。

4 仿真實驗

為對基于連續(xù)測角的被動測距方法的可行性和適用性進行驗證[8]，分別用擴展卡爾曼濾波算法（EKF）、修正協(xié)方差的擴展卡爾曼濾波算法（MVEKF）、修正增益的擴展卡爾曼濾波算法（MGEKF）和不敏卡爾曼濾波算法（UKF）進行了仿真實驗。仿真實驗參數(shù)設(shè)置為：目標(biāo)在相對載機初始距離為70 km處作勻速直線運動，速度230 m/s，載機在x方向上作勻速直線運動，速度250 m/s，在y方向上作S形機動。光電雷達掃描周期T=1 s，掃描次數(shù)N=200，初始距離取為100 km，距離的標(biāo)準差為10 km，速度的標(biāo)準差為100 m/s，測量噪聲標(biāo)準差取為σθ=σφ=2 mrad。采用蒙特卡洛方法對跟蹤濾波器進行仿真，仿真次數(shù)為100次。

4.1 系統(tǒng)可觀測性驗證

上述討論了載機機動是系統(tǒng)可觀測的必要條件，仿真實驗的驗證結(jié)果如圖2所示。

圖2 系統(tǒng)可觀測性驗證Fig.2 Validating the observability of system

由圖2可以發(fā)現(xiàn)這幾種濾波算法仿真的結(jié)果均是完全偏離真實軌跡，無法完成測距，可見在載機不作機動的情況下，系統(tǒng)是不可觀測的。

4.2 濾波算法比較

在相同的仿真條件下，選用EKF、MVEKF、MGEKF和UKF 4種濾波算法，對其濾波效果進行比較，仿真結(jié)果如圖3所示。

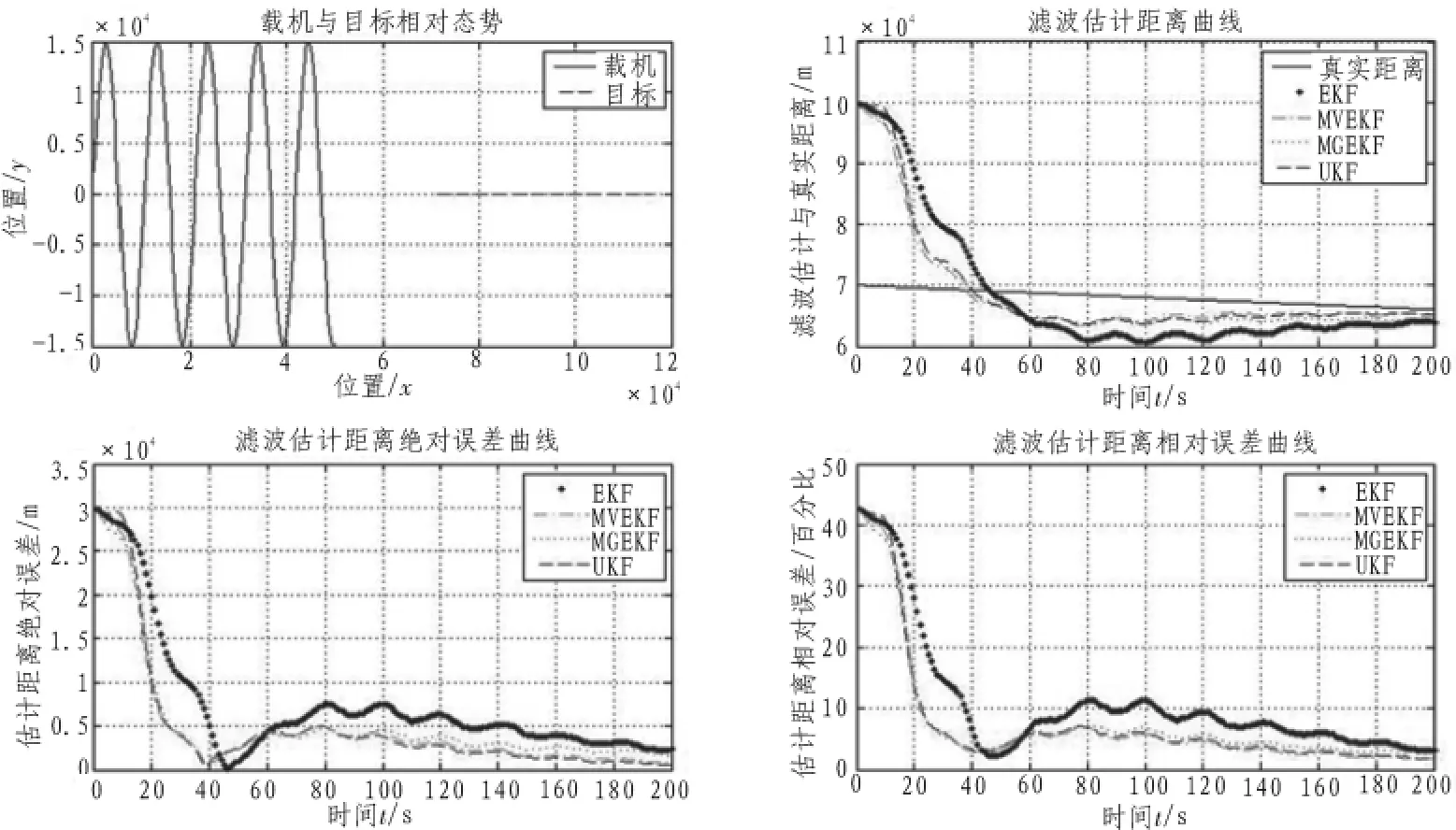
圖3 仿真實驗濾波估計曲線圖Fig.3 Graph diagram of the simulation

由圖3可以看出，在載機作S形機動的情況下，幾種濾波算法都很好的完成了收斂，并獲得了距離的估計值。這幾種濾波算法的最終估計精度都達到了5%以內(nèi)，具有較高的精度。

MVEKF、MGEKF和UKF均在20 s左右就可以迅速完成收斂，EKF則在40 s左右進入收斂。這4種濾波算法中，MVEKF、MGEKF和UKF的濾波效果差別不大，均比EKF的濾波效果要好。

5 飛行實驗

為了對此被動測距方法的可行性和適用性進行驗證，組織了飛行實驗。通過光電雷達記錄的實驗數(shù)據(jù)，對此方法的被動測距效果進行分析和評價。

飛行實驗中，載機作S形機動，目標(biāo)機作勻速直線運動，在空間直角坐標(biāo)系下其運動狀態(tài)如圖4所示。

圖4 載機與目標(biāo)相對運動態(tài)勢圖Fig.4 Situation map of the relative motion between the plane and the target

用EKF、MVEKF、MGEKF和UKF 4種算法進行被動測距，濾波估計曲線如圖5所示。

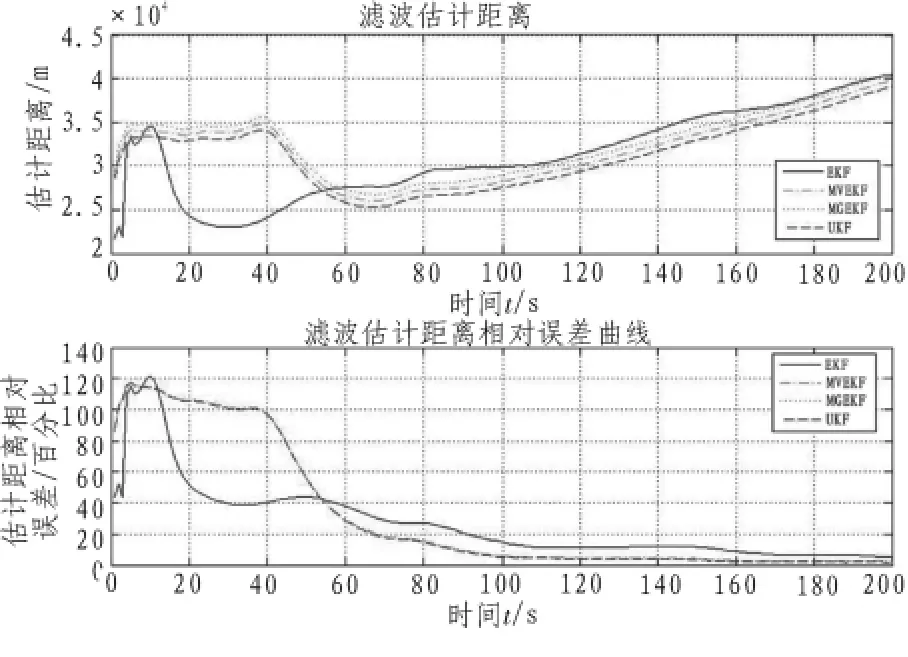
圖5 飛行實驗濾波估計曲線Fig.5 Graph of the flight experiment

通過飛行實驗，基于連續(xù)測角的被動測距方法得到了目標(biāo)最終的距離值和相對誤差，列表如表1所示。

表1 實驗結(jié)果比較Tab.1 Comparision of experiment results

由圖5和表1可以看出，實驗所測得的目標(biāo)距離精度較高，濾波算法獲得的精度值均達到了5%以內(nèi)。實驗表明，該測距方法能夠應(yīng)用于工程實踐中，具有很高的實用價值和現(xiàn)實意義。

6 結(jié)論

本文基于連續(xù)測角的被動測距方法，在空間坐標(biāo)系中構(gòu)建了系統(tǒng)模型，對其可觀測性進行了分析，得出載機機動是系統(tǒng)可觀測的必要條件。然后通過仿真實驗和飛行實驗，對該測距方法的可行性與實用性進行了驗證。

基于連續(xù)測角的被動測距技術(shù)通過觀測目標(biāo)的角度信息，建立合適的系統(tǒng)模型，選用合適的濾波算法，可以估測出目標(biāo)的距離值。這種測距方法精度高，收斂快，效果好，是無源定位系統(tǒng)中一種重要的測距手段。

[1]趙勛杰，高稚允.光電被動測距技術(shù)[J].光學(xué)技術(shù)，2003，29，（6）：652-656.

ZHAO Xun-jie,GAO Zhi-yun.Opto-electrical technique of passive detection[J].Optical Technology,2003,29（6）:652-656.

[2]馮道旺，李宗華，周一宇等.一種單站無源定位方法及其可觀測性分析[J].國防科技大學(xué)學(xué)報,2004，26（1）：68-71.

FENG Dao-wang,LI Zong-hua,ZHOU Yi-yu，et al.A method of single-step passive location and the analysis of its observability[J].Journal of National University of Defense Technology,2004,26（1）:68-71.

[3]何友，修建娟，張晶煒，等.雷達數(shù)據(jù)處理及應(yīng)用[M].北京：電子工業(yè)出版社，2006.

HE You,XIU Jian-juan,ZHANG Jing-wei，et al.Processing and analysis of radar data[M].Beijing Publishing House of Electronic Industry,2006.

[4]Guerci J R，Goetz R A.A method for improving extended Kalman filter performance for angle-only passive ranging[J].IEEE Transactions on Aerospace and Electronic System，1994，30（4）:1090-1093.

[5]趙國偉，李勇，李滔.基于MVEKF算法的機載單站無源定位[J].西北工業(yè)大學(xué)學(xué)報，2007，25（1）：113-116.

ZHAO Guo-wei,LI Yong,LI Tao.Algorithm for passive location based on MVEKF[J].Journal of Northwestern Polytechnical University,2007，25（1）:113-116.

[6]浦甲倫，韋常柱，容思遠.修正增益卡爾曼濾波算法在被動測距問題中的應(yīng)用[J].宇航學(xué)報，2007，28（4）：886-889.

PU Jia-lun,WEI Chang-zhu,RONG Si-yuan.The application of MGEKF in the passive detection[J].Journal of Astronautics,28（4）:886-889.

[7]王淑一，程楊，楊滌，等.UKF方法及其在方位跟蹤問題中的應(yīng)用[J].飛行力學(xué)，2003，21（2）：59-62.

WANG Shu-yi,CHEN Yang,YANG Di，et al.UKF and its application to bearings-only tracking problem[J].Flight Dynamics,2003,21（2）:59-62.

[8]張艷桃，袁兆強.基于雙端不同步采樣的同桿雙回線故障測距算法[J].陜西電力,2009,37（9）:38-41.

ZHANG Yan-tao,YUAN Zhao-qiang.Two-terminal asynchronous data based fault location algorithm for double-circuit transmission lines on one pole[J].Shaanxi Electric Power,2009,37（9）:38-41.