公路斜交板橋的設計及交角的影響
張建成
(石家莊市公路橋梁建設集團第五公路工程處)
0 概 述
隨著現代交通的發展,公路斜交橋越來越多,這是因為它最容易滿足各種線型要求。無論是跨越斜交河流、通道,還是位于縱橫坡或超高段,斜交橋都能做的順適得體。斜交橋的幾何形狀具有很好的可塑性。
在 20世紀六、七十年代,人們盡量避免斜交橋,或者硬性把橋扭成正交,或者改變路線走向,正交過河。這除了施工放養較為復雜外,和斜交橋的受力不明確也不無關系。目前對斜交橋仍采用經驗的、近似的辦法進行計算。計算結果不像正交橋那樣令人放心。在橋梁檢查時,對斜交板這樣那樣的裂縫,要做出準確的原因分析和對策,往往是很困難的。
在斜交板設計中,各國都有各自的設計方法。目前,已積累了大量的實例資料,并開始采用有限元分析,概括介紹如下。
1 中國規范的計算方法
關于跨長、板寬及斜交角的定義當斜橋為現澆板時,我們認為他是整體式板。
當交角 φ<15°時,可按正交板計算,但所取計算跨長還要按跨寬比(1/b)而定:當板寬較寬時(1/b≤1.3),取蓋梁間的垂直距離L1為計算跨經;當板寬較窄時(1/b>1.3)時,取斜跨 L為計算跨徑。
在工程實踐中經常會遇到 φ>15°的情況,現行規范未明確指定計算方法。“規范說明”中參考了奧爾森的試驗結果:
(1)跨寬比l/b≥1.3時,只要φ≤40°,均按正交橋計算,計算跨徑取斜跨;
(2)跨寬比l/b=1.3~0.7時,當φ<15°時按正交計算,計算跨徑取正跨;當 15°<φ<40°時計算跨徑取1/2(斜跨+正跨);
(3)跨寬比l/b<0.7時,只要φ≤40°,一律按正交設計,計算跨徑取正跨。
當斜交橋為預制板時,我們認為板間連接只傳遞剪力,內力計算時視一塊板為一個受力單元,按單向板計算。
2 美國規范(AASHTO)的計算方法
建議,當斜交角小于 30°時,斜交板可以按同跨度的正交板計算而不加修正;當斜交角大于 30°時,需用其他計算格式進行計算。
該規范首先把車輪荷載進行橫向分布,然后把整體板分成若干條小梁進行分析。這樣就把雙向彎曲問題簡化成了單向彎曲問題。先求出一個車道內的彎矩和剪力,再除以車道寬度,便可以求出單位寬度板內的彎矩和剪力。
另外還有一種簡單的算法:斜交板的內力等于正交板的內力乘以折減系數,該系數γ≤1.0。即

式中:φ為斜交角,通過試算可知,當 φ<12°時,γ=1.0,可以不進行修正。
3 FEA計算方法和試驗結果
利用SAP2000程序,進行三維有限元分析(FEA),是一種精確的計算方法。所取變量有跨長、板寬和斜交角。計算結果表明,AASHTO方法大部分情況都偏于保守,尤其是偏角很大時,它過高的估算了縱向最大彎矩。
斜交橋與正交橋比較:設定Mφ為斜跨橋彎矩,M0為正交橋彎矩,則 Mφ/M0隨著斜交角度的增大而減小。在 φ<20°時,Mφ/M0≈1.0;當φ為30°~40°時,Mφ/M0=0.75;當φ達到 50°時,該比值可達0.5,即斜橋彎矩只有正橋彎矩的一半。與這一趨勢相似的是斜板的活載撓度:斜交角φ為20°時,撓度比正交橋下降 10%;φ為 30°時,下降 25%;φ為40°~50°時,撓度可下降 40%。
4 斜板的配筋
順橋軸方向的縱向鋼筋,按計算出的彎矩進行配置。板的自由邊緣帶可認為是一片“邊梁”(約為 0.5m),通常要多配一些鋼筋,一般不少于3根。斜交板的交角在15°以下時,主筋的方向和正交一樣,即沿著橋梁縱軸線方向配置;但取正跨為計算跨徑時,主筋應沿著正橋方向布置,通常當φ>15°時應按正橋方向布置。
特別應該注意的是,鈍角部位受力復雜,應配置加強鋼筋:頂層加強鋼筋方向應垂直于鈍角平分線;底層加強筋應平行于鈍角平分線;鋼筋直徑不小于 12mm,間距 10~15cm。
與正交橋不同,斜交橋的橫向鋼筋不單單是起分布作用,它還有承受彎矩的功能。隨著斜角度的增大,橫向彎矩也在增大,所以順時的橫向鋼筋應按受力筋考慮。配置數量可按縱向主筋的百分比控制,百分比n可按下式計算
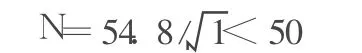
式中:L為跨徑,m;n值不超過50%。如L=9m時,n= 54.8=18,即橫向配筋率應為縱向主筋的 18%。
5 結 論
(1)當斜交角度不大于 20°時,按有限元法和按規范求得的最大縱向彎矩基本相同。
(2)當交角增大時,美國AASHTO規范過大的估算了最大彎矩:當 φ為 30°時,多算了 20%;當 φ為 40°時,多算了50%;當φ達到 50°時,多算了 100%。
(3)斜交橋與正交板相比:設斜交橋彎矩與正交橋彎矩之比為n。當交角為 20°時,n=1.0;當交角為 30°~40°時, n=0.75;當交角增至50°時,n=0.5。
(4)當斜橋的縱向彎矩減小時,橫向彎矩卻在增大。
(5)隨著交角的增加,最大活載撓度在減小,趨勢與縱向彎矩相似。當交角大到40°~50°時,撓度可減小到正交橋的0.6。
(6)一般認為,斜角角度不大于 20°時,可按正交橋計算,當交角大于 20°時,應按三維有限元法進行分析。

