多分類支持向量方法的本科招生生源質量模型

邢 濤，廖 冉

(1.北京航空航天大學經濟管理學院，北京100191，xt@buaa.edu.cn; 2.北京航空航天大學數學與系統科學學院，北京100191)

近年來，高等教育已從“精英教育”快速向“大眾化教育”轉變，高校招生規模逐年擴大，使得高校在生源上競爭日趨激烈.怎樣從全國的高考生中錄取更多的優質生源，成為各高校招生工作者的一大難題.各高校招生工作部門一直在積極探索一套科學、有效、完善的招生管理和評價體系［1］.在現行招生制度下，高考成績仍然是絕對性指標.隨著高校招生改革的推進，高考自行命題省份不斷增加，高考也從最初的全國統一標準變得更具區域性特色.因此，如何在兼顧教育公平的原則下，合理安排招生計劃，從而在全國眾多的報考學生中科學、公正、高效地挑選出有發展潛力的優秀學生是提高生源質量的關鍵問題.以往的高校本科招生生源分析，并未充分挖掘高校歷年已錄取的學生信息.教育的發展具有持續性，一個地區以往的生源質量往往能夠反映出該地區的教育水平，從而指導今后的招生工作，而高校本身擁有的龐大的學生信息資源也恰好利于這一方法的實施.

統計學習理論是專門研究有限樣本情形下的機器學習規律的理論，在這一理論基礎上發展出了一種通用學習算法，相比起傳統統計方法所采用的經驗風險最小化原理，支持向量機算法采用了結構風險最小化理論并體現出了優于傳統統計方法的一些性能［2］.多分類支持向量機算法是傳統支持向量機算法的推廣，該算法不僅繼承了支持向量機算法穩健且計算精確等特點，而且克服了傳統支持向量機算法只能解決二分類問題的局限.

本文利用多分類支持向量機算法，根據各地區學生在大學期間的學習成績，與學生入學前的信息特點，探討本科生源質量預測體系，建立本科生源質量分析模型，為高校制定招生計劃、提高生源質量提供有效的參考信息.該模型可以對高校的招生工作給出初步的參考.

1 支持向量機

支持向量機算法是建立在統計學習理論的結構風險最小化原理基礎上的，能較好地解決小樣本問題，同時具有很好的泛化能力.算法由Vapnik等［3］在1995年左右提出.近些年來，該算法在實際應用及理論推導中都有著長足的進步.韓媚和郭丹鳳［4］將支持向量機方法應用到了高校就業情況的分析中.向小東和宋芳［5］利用基于核主成分分析的支持向量機算法對福建省的失業率進行了有效的預測和分析.相比其他傳統的統計學分類方法或是帶有學習過程的人工智能算法，如神經網絡方法，支持向量機算法能夠克服過學習問題和維數災難問題，具有全局最優的特點和很好的泛化能力［3］.該算法主要有以下兩個特點［6］:

(1)采用結構風險最小化原則，所得到的學習機器有著很好的泛化能力，即由有限的訓練樣本得到的小誤差能夠保證對獨立的測試集仍保持小的誤差.

(2)支持向量機算法最終將轉化為一個凸優化問題，局部最優解一定是全局最優解.

支持向量機算法的基本思想是在樣本空間或者特征空間，構造出最優超平面，盡可能將不同類的數據點分開，并使得超平面與不同類數據點之間的距離最大，從而達到最大的泛化能力.在線性可分情況下，如圖1所示，圓圈和方塊分別代表兩類樣本點，每類中處在邊界的點為支持向量，這些支持向量所形成的超平面H1和H2為能撐起不同類別樣本點的分類超平面，其之間的間隔為類與類之間的最大間隔，因此最佳的分類面H0介于這兩個分類超平面之間.

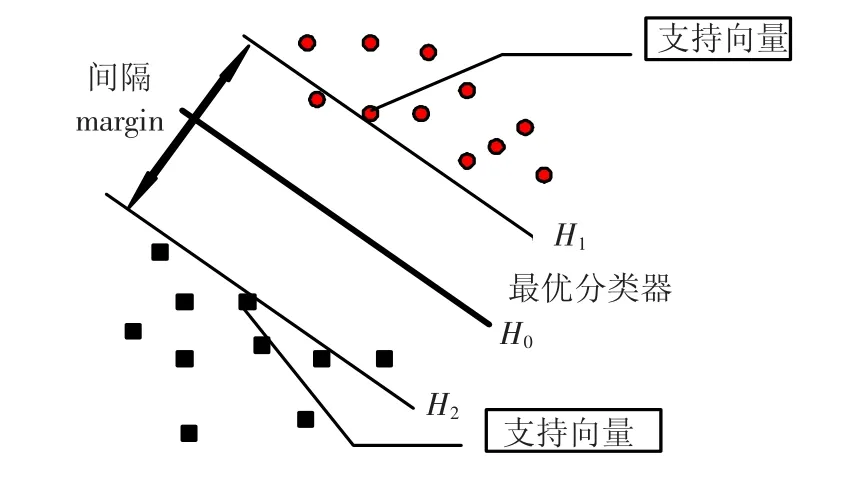
圖1 線性可分下的支持向量機模型

假設樣本集合為S={(xi，yi)∈Rn×{±1}，i=1，…，m}，其中x為輸入樣本，y為輸出樣本.用x∈A，y=1表示一類點，x∈B，y=-1表示另外一類點.算法的目標是利用訓練樣本提供的信息來估計一個分類器，即函數f:Rn→{±1}.如果訓練樣本是線性可分的，那么必然存在(w，b)∈Rn×R使得wTx+b=0為其線性邊界，且滿足wTx+b≥1(x∈A)和wTx+b≤-1(x∈B).該限制條件可被表示為:yi［(wT·xi)+b-1］≥0，得到決策函數:fw，b(x)=sign(wTx+b)，其中w為權重向量，b為偏離值.最終該問題可以轉化成為求解如下二次優化問題:

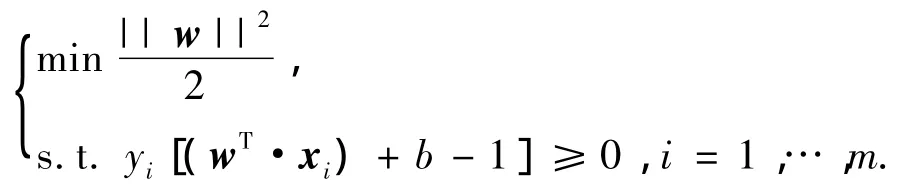
然而，在實際問題中常常遇到線性不可分的情形，支持向量機算法的優勢也體現在其能處理非線性復雜系統中的問題，它能通過非線性變換將該非線性問題轉化成為某個高維空間中的線性問題，在高維空間中求取最優分類面實現線性分類.這種非線性變換是通過定義適當的核函數實現的，在本文中特別應用到了希爾伯特再生核空間HK

［7］中的兩種常用的核函數，其定義如下:

高斯核函數:

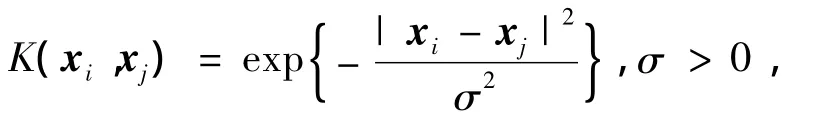
多項式核函數:

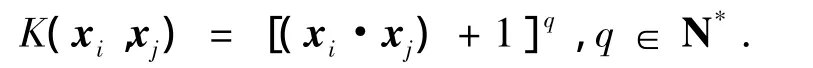
2 多分類支持向量機

支持向量機的產生最初是為了解決二分類問題，但在實際應用中，往往要求算法可以對多于兩類的分類問題給出準確的判斷.因此，隨著實際應用的廣泛要求和理論研究的深入，多分類支持向量機算法就此產生.

多分類支持向量機算法在很多領域中都有著廣泛的應用，Yoonkyung Lee等［8］應用多分類支持向量方法對基因表達譜數據和衛星放射數據進行了分析.Dirong Chen等［9］對多分類支持向量機算法的收斂性給出了理論分析.竇智宙等［10］應用該方法對彩色癌癥細胞的圖像進行了分割.康文雄等［11］應用小波分解和多分類支持向量機算法處理了臉譜識別問題.

2.1 多分類問題及貝葉斯決策

在多分類問題中，考慮如下樣本(xi，yi)，i= 1，…，m.，其中，xi∈Rd為輸入樣本，yi∈{1，2，…，k}為輸出，代表了輸入樣本的分類情況.主要目標是找到一種分類法則，使得分類法則φ(x)可以盡可能精準的刻畫輸入xi和輸出yi之間的關系.假設樣本為獨立采樣且滿足分布P(x，y)，pj(x)=P(Y=j|X=x)表示樣本x被分到第j類的概率，當各類別之間的錯分誤差相等時，分類法則φ(x)的損失可由如下函數定義:

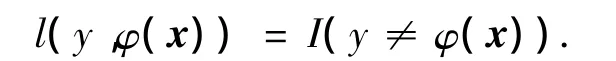
其中:I(·)為勢函數，若自變量為真，則取值為1，為假則取值為0.此時，最佳的分類法則為貝葉斯分類，即

當錯分誤差不一樣時，定義矩陣C，Cjl表示第j被錯分到l的懲罰.顯然有Cjj=0，j=1，2，…，k，此時

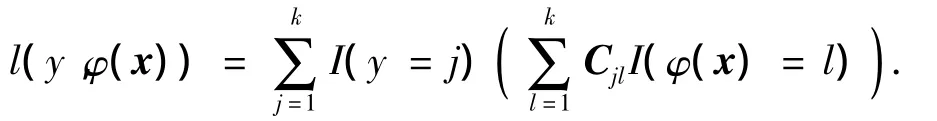
通過最小化風險函數得到的最優分類器為

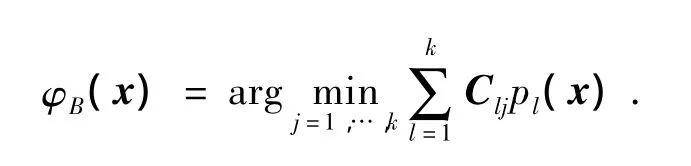
但在實際問題中，往往需要定義不同的錯分懲罰，遇到這樣的情況可以通過調整矩陣C中的元素值來表示不同的錯分誤差.

2.2 一對一(one against one)多分類支持向量機的數學模型

傳統的SVM算法是專門處理小樣本問題的，因此在考慮多分類問題時可以將問題轉化成為多個二分類問題，這樣的多分類支持向量機算法稱為一對一的多分類算法［12］.

一對一分類是在k類訓練樣本中構造所有可能的兩類分類器，每個分類器僅僅在k類中的兩類訓練樣本上訓練，結果共構造k(k-1)/2個分類器，測試樣本經過各個分類進行分類，每次將樣本判為某一類，最終得到判入次數最多的類為樣本的最后結果.但這種算法的運算量大，計算步驟很多，相應的運算時間也會長.

2.3 一對多(one against all)多分類支持向量機的數學模型

一對多方式的主要思想是構造k個二分類器，每個二分類器應用于所有樣本，第i個二分類器將樣本分為第i類和其他類，這k個二分類器組合起來就可以形成N分類的判決函數.當一個樣本數據輸入時，依次用這k個二分類器進行判斷，如果第i個二分類器的輸出是屬于第i類，而其他的分類器都輸出為其他類，則判斷該樣本屬于第i類.

多分類支持向量機算法最終轉化為求解如下優化問題:

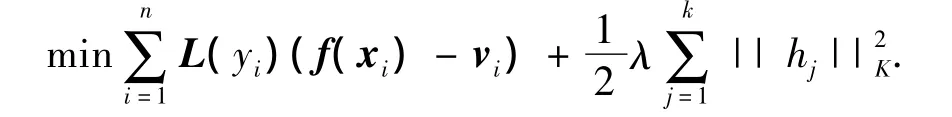
其中:向量vi∈Rk記錄分類結果，如果樣本xi屬于第j類，則向量vi第j個元素為1，其他元素為-(k-1)-1;且映射L(yi)第j個元素為0，其他元素為1的向量，滿足限定條件)=0.該問題的最優解的算法求解過程本文借助libsvm工具包［13］中SVMtrain函數完成.

3 高校生源質量分析模型

基于多分類支持向量機的生源質量分析模型由數據采集、數據預處理、特征指標選取、數值歸一化和學習過程組成，如圖2所示.

圖2 多分類支持向量機模型

1)數據采集器.按用戶要求從數據庫中采集數據;

2)數據預處理.剔除殘缺數據和奇異數據，如各省份特招生的樣本.由于各個省份的錄取標準不同，分數之間的差距也很大，所以對高考成績進行層次化處理，共分為11檔次，如表1所示.

表1 高考成績分層處理

3)特征指標選取.從學生信息庫中依照數據的屬性和對問題的貢獻選取了省份、高考成績、所在省份排名、畢業時所在專業排名情況這4個指標組成了樣本的有效信息(見表2).

表2 有效樣本

4)數值歸一化處理.由于各個指標之間數值的差別很大，所以對數值進行歸一化處理，使得數值分布在［-1，1］之間:

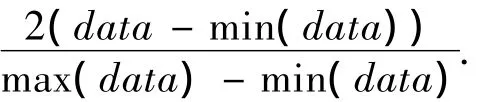
5)訓練及學習過程.對有標號的樣本，根據其畢業時所在專業的排名進行分類(見表3):

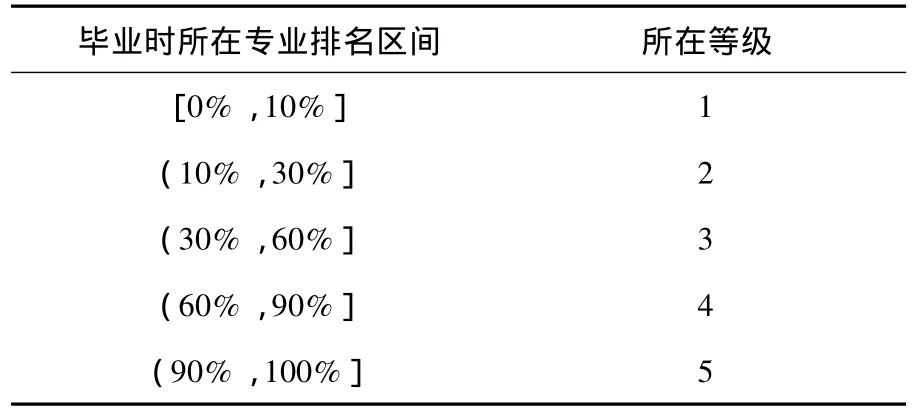
表3 帶標號樣本的分類情況

4 測試實例與分析

數據來源主要是某大學某年級3 000余名本科學生的數據.其中包括學生入學時的高考成績以及在高中時期的其他信息(包括是否是三好學生、優秀學生干部，是否在學科競賽中獲獎等)，另外一部分信息如生源所在省，錄取時所在省份的排名情況以及高考成績.研究的數據量足夠大，具有普遍性，使分析結果具有一定說服力.

4.1 多分類支持向量機模型的分類情況

實驗基于高斯核函數及多項式核函數展開，并選取了不同核寬及不同的階數進行了對比，在表4中，MSVM表示多分類支持向量機模型，RBF-1表示核寬為1的高斯核，POLY-1表示階數為1的多項式核.在實驗過程中，采用10倍交叉驗證方法(10-fold cross validation)測試各個模型的分類結果，即將數據集分成10組，輪流將其中9組做訓練，1組做測試，10次的結果的均值作為對算法精度的估計，結果分別呈現了均值和波動值.

為比較多分類支持向量機的分類效果，采用多元統計中的判別分析作為對比試驗.判別分析是經典的多元統計方法，其主要思想是在分類確定的條件下，根據某一研究對象的各種特征值判別其類型歸屬問題的一種多變量統計分析方法.其基本原理是按照一定的判別準則，建立一個或多個判別函數，用研究對象的大量資料確定判別函數中的待定系數，并計算判別指標.據此即可確定某一樣本屬于哪一類.實驗結果見表4.

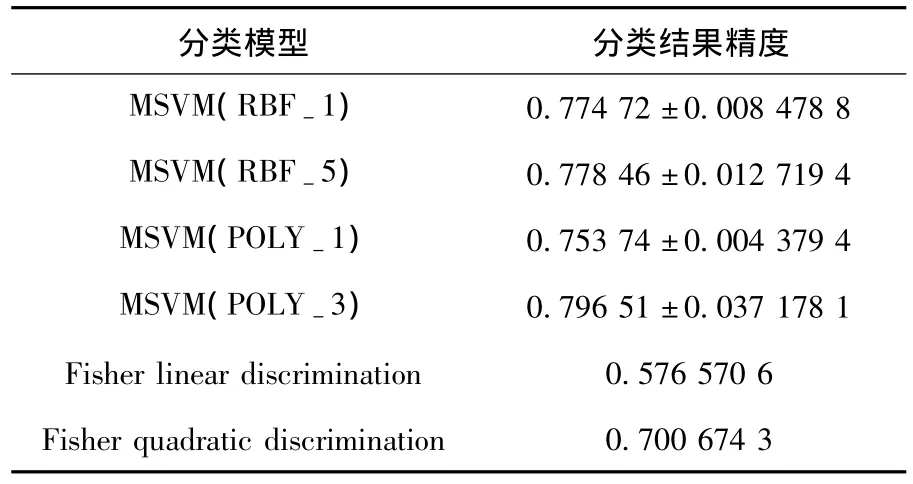
表4 實驗結果(1)

通過實驗可以看出，多分類支持向量機模型較傳統判別分析模型有著更好的分類能力.

4.2 模型的改進

考慮對多分類支持向量機模型進行改進，在如上的實驗中均假設對錯誤分類的懲罰是一致的，但在實際情況中并不是如此.例如一種誤差是將一名一等的學生錯分為二等，即優秀的被判別成良好.另一種誤差是將一等學生錯分到五等，即將優秀的學生判別成差下.這兩種錯誤的程度顯然不一樣，第二種錯誤較第一種錯誤要嚴重些，因此，可以調整懲罰矩陣Cjl，在本問題中最終用到的懲罰矩陣為

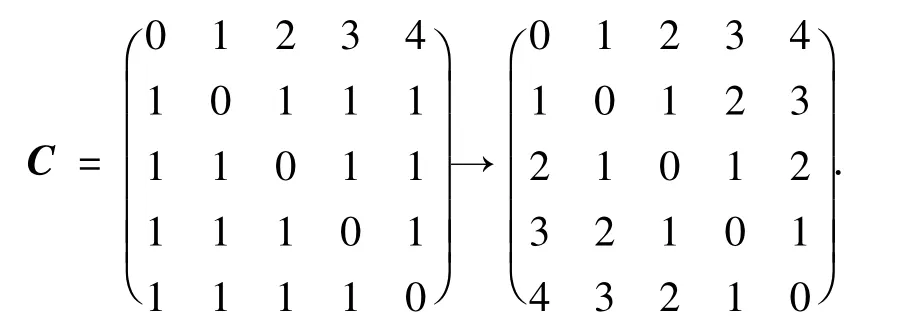
含義為將第i類學生錯分到第j的懲罰為|i-j|.

基于此調整，訓練得到新的分類器，實驗結果如表5所示.

表5 改進后的實驗結果

由模型的實驗結果可以看出，分類結果精度較調整前有了較大的提高.

5 結論

1)本文基于多分類支持向量機算法建立了生源質量分析模型，該模型可以通過生源所在地、高考成績，以及該成績所在省的排名等信息，預測出該生源在大學畢業時學習情況的所處類別，因此可以對生源的質量優劣進行初步的分析和評價，對招生工作及相關政策的制定有一定的指導和幫助.

2)通過對懲罰矩陣進行合理的調整，模型的結果和可靠性都得到顯著的提高.

［1］姚金琢.高等教育大眾化與依法試行自主招生問題探析［J］.中國高教研究，2006(11)，90-91.

［2］于春梅，楊勝波，陳馨，等.SVM和基于PCA、PLS的 SVM在非線性辨識中的比較研究［J］.計算機應用研究，2004，24(6):85-90.

［3］VAPNIK V.The nature of statistical learning theory［M］.［S.l.］:Springer Verlag，1995.

［4］韓媚，郭丹鳳.SVM的特征選擇方法在高校就業預測中的應用研究［J］.杭州師范大學學報:自然科學版，2009，8(5):358-362.

［5］向小東，宋芳.基于核主成分與加權支持向量機的福建省城鎮登記失業率預測［J］.系統工程理論與實踐，2009，29(1):73-80.

［6］祁享年.支持向量機及其應用研究綜述［J］.計算機工程，2004，30(10):6-9.

［7］SCH?LKOPF，SMOLA A.Learning with Kernels［M］. Cambridge:MIT Press，2002.

［8］LEE Y K，LIN Y，WAHBA G.Multicategory support vector machines，theory，and application to the classification of microarray data and satellite radiance data［J］. Journal of the American statistical Association，2004，99 (465):67-381.

［9］CHEN D R，XIANG D H.The consistency of multicategory support vector machines［J］.Adv Comput Math，2006，24(1-4):155-169.

［10］竇智宙，平子良，馮文兵，等.多分類支持向量機分割彩色癌細胞圖像［J］.計算機工程與應用，2009，45 (20)，236-239.

［11］康文雄，謝紀美，鄧飛其，等.基于小波分解和多分類支持向量機的臉譜識別［J］.計算機測量與控制，2005，13(12):1390-1422.

［12］HSU C W，LIN C J.A Comparison of Methods for Multiclass Support Vector Machines［J］.IEEE Trans Neural Networks，2002，13(2):415-425.

［13］CHANG C C，LIN C J.LIBSVM:a library for support vector machines［EB/OL］.［2008-07-25］.http:// www.csie.ntu.edu.tw/～cjlin/libsvm.