Robust Stability Criterion for Uncertain Neural Networks with Time Delays

LIN Zhi-wei(林知微)，ZHANG Ning(張寧)，YANG Hong-jiu(楊洪玖)

(1.School of Automation，Beijing Institute of Technology，Beijing 100081，China;

2.College of Marine Engineering，Northwestern Polytechnical University，Xi'an 710072 Shaanxi，China)

Introduction

Recently，more and more attention has been paid to the stability analysis problem of neural network with time-delay，and many useful and sufficient conditions have been proposed to ensure the asymptotic or exponential stability of neural network.It should be pointed out that the uncertainties of various neural networks are unavoidable due to many reasons，such as modeling error，measurement error，linearization approximation，and so on.To solve this problem，the robust stability problem of uncertain neural network with time-delay was studied extensively［1－4］.In Ref.［1］，the author studied the global robust stability of delayed cellular neural network with norm-bounded uncertainties，but the criteria in Ref.［1］are delay-independent，which are conservative compared to the delay-dependent criteria when the delay is small.In Ref.［2］，the global robust stability of interval Hopfield-type neural network was studied.The robust stability of cellular neural networks with delay was investigated in Ref.［3］via the linear matrix inequality approach.The robust stability of neural network with time-varying and norm-bounded uncertainties was studied in Ref.［4］，but the stability criteria are also delay-independent.Hence，it is important to develop the delay-dependent stability criteria for delayed neural network.

The stability of neural network with time varying delay has been investigated extensively［4－6］.Unfortunately，the time-varying delay function is always assumed to be continuously differentiable，and its derivative does not exceed unity［4，6］，which is very restrictive.In Ref.［5］，this restrictive constraint was removed，and some sufficient conditions were derived，but the results in Ref.［5］do not contain the information of the derivative of time-varying delay function.

Based on the above research，the robust stability problem of uncertain neural network with time-varying delay was considered in this paper.The uncertainties are norm-bounded，maybe time-varying.The restriction on the derivative of time-varying delay function is removed，and the time-varying delay function may be not continuously differentiable.Some new delay-dependent stability criteria were presented in terms of linear matrix inequalities(LMIs)，in which the information of the derivative of the time-varying delay function was included.

A numerical example was given to illustrate the effectiveness of the developed technique.

1 Problem Description

Consider the following uncertain neural network with time-varying delay

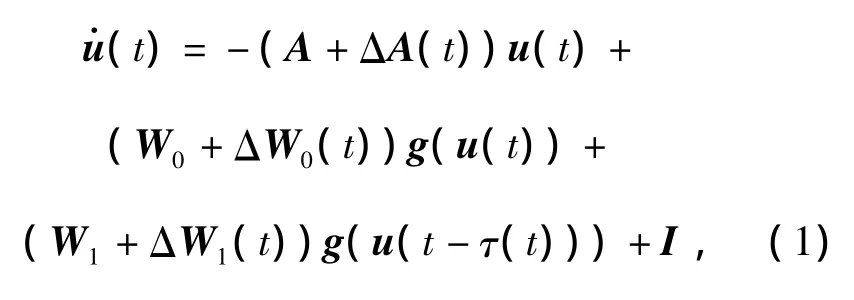
where u(t)=［u1(t)，u2(t)，…，un(t)］T∈Rnis a neural state vector;A=diag{a1，a2，…，an}is a diagonal matrix，where ai＞0，i=1，2，…，n;W0∈Rn×nand W1∈Rn×nare the correlative weight matrices;ΔA(t)，ΔW0(t)and ΔW1(t)are parametric uncertainties;τ(t)is the time-varying delay，meeting 0≤whereand d are constants;I is a constantexternalinputvector;g(u)=［g1(u1)，g2(u2)，…，gn(un)］T∈ Rnis the neuron activation function.

The uncertain matrices ΔA(t)，ΔW0(t)and ΔW1(t)are defined as follows

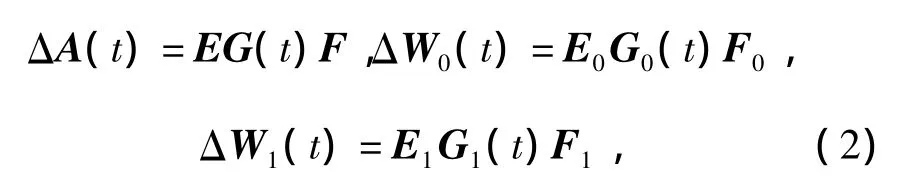
where E，E0，E1，F，F0and F1are known constant matrices with appropriate dimensions;G(t)，G0(t)，and G1(t)are the time-varying uncertain matrices，which is given by

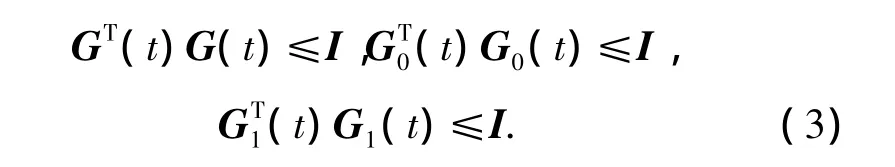
The neuron activation function gi(ui)is assumed to be continuous differentiable，monotonically increasing and bounded，but in many cases，such as in electronic circuit，it may be neither monotonically increasing nor continuously differentiable.Therefore，here we suppose that gi(ui)is bounded and satisfies

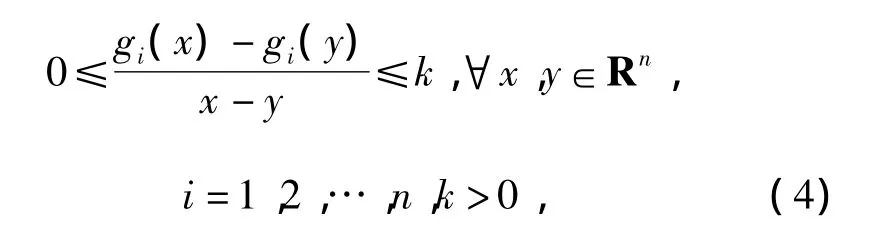
where k is a constant，n is a integer.

It is well known that，from above assumption and Brouwer's fixed point theorem，System(1)has at least one equilibrium point u*=［u*1，u*2，…，u*n］T∈Rnfor a given constant I.Hereafter we will prove the global asymptotic stability of the equilibrium point and its uniqueness.

For the sake of convenient discussion，the equilibrium point u*is shifted to the origin by transforming x=u－u*，and after calculation，System(1)can be rewritten into the following form

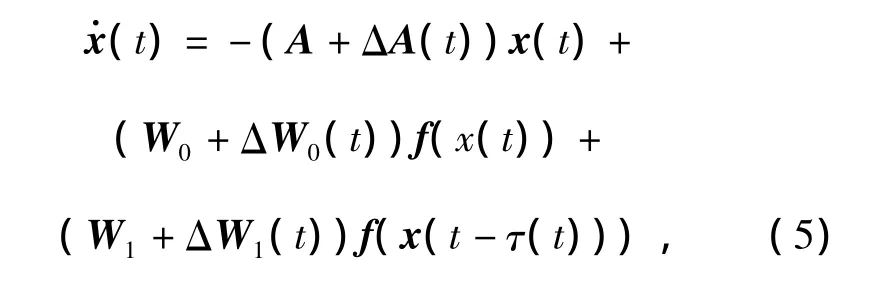
where x= ［x1，x2，…，xn］T∈ Rnandf(x)=［f1(x1)，f2(x2)，…，fn(xn)］T∈Rn.It can be known from Eq.(4)that the transformed neuron activation function is

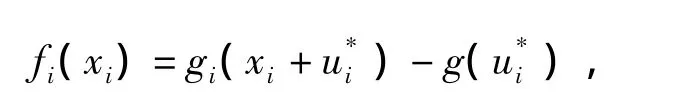
satisfing

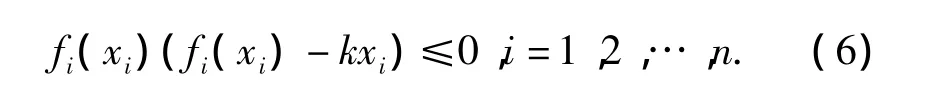
2 Main Results

In this section，we will analyze the robust stability of uncertain neural network with time-varying delay described by Eq.(5).The first result deals with the stability of the system without uncertainties，that is，

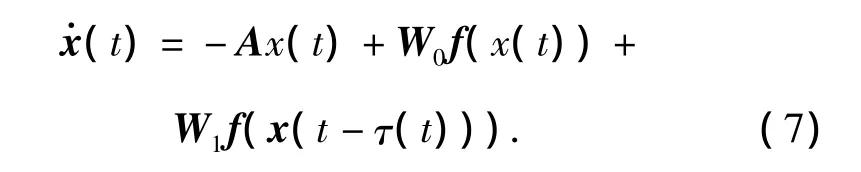
Based on the Lyapunov-Krasovskii stability theorem，we have the following theorems.

Theorem 1If there exist the real matrices P1，P2，X12，X13，X23，W0，W1，the symmetric positive definite matrices P，Q，R，X11，X22，X33and the diagonal matrices S＞0，T＞0 such that the following LMIs hold:

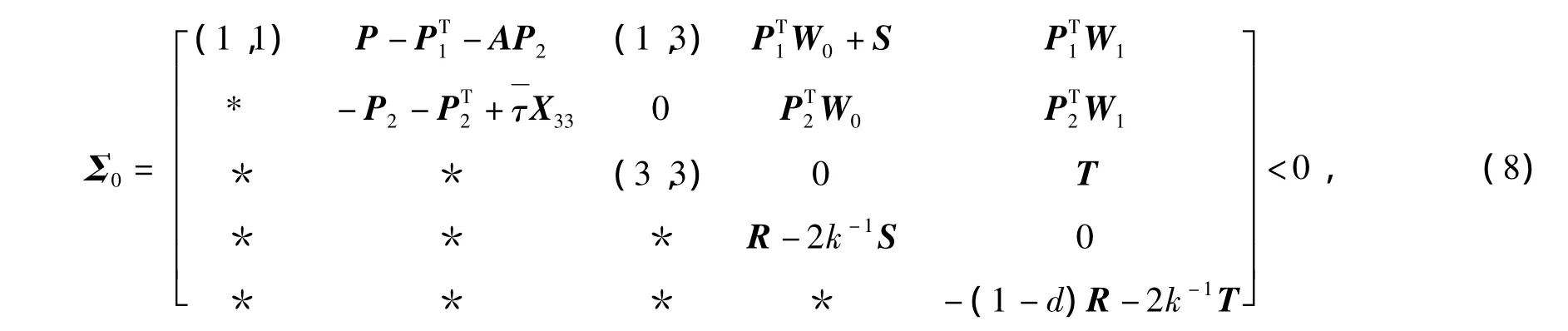
where

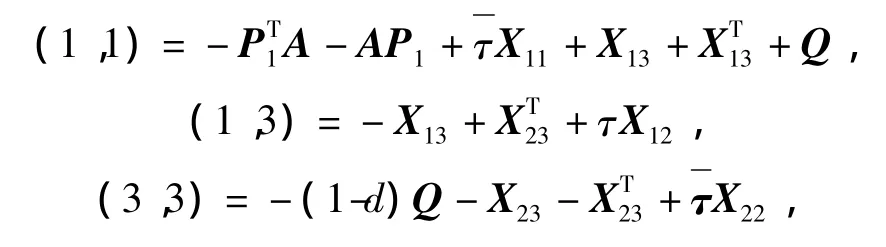
and

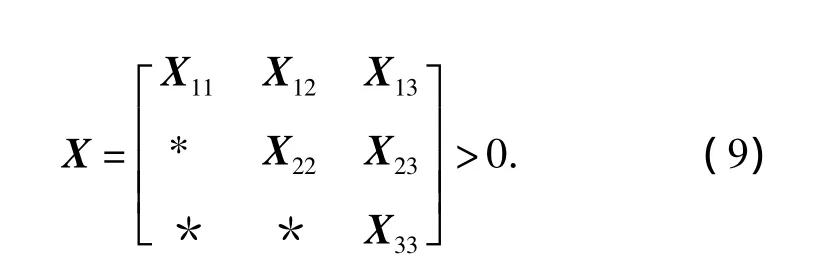
then System(7)is asymptotically stable.

In all the matrices，* denotes the symmetric terms in a symmetric matrix.

Proof Construct a positive Lyapunov-Krasovskii function:

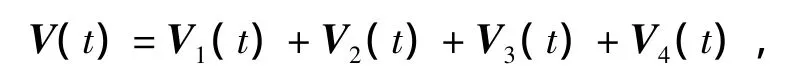
where

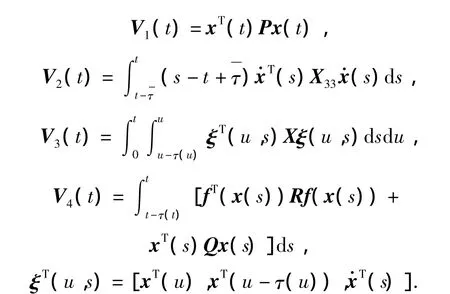
Taking the derivative of V(t)along the trajectory of System(7)，then we have

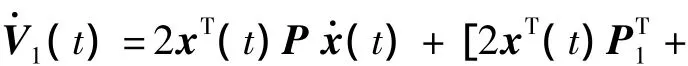
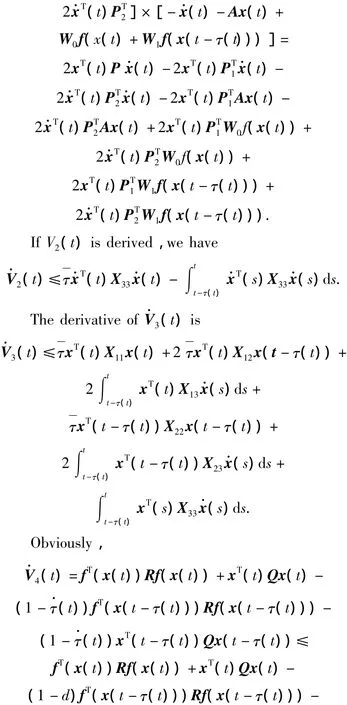
(1 －d)xT(t－τ(t))Qx(t－τ(t)).

Finally，we have

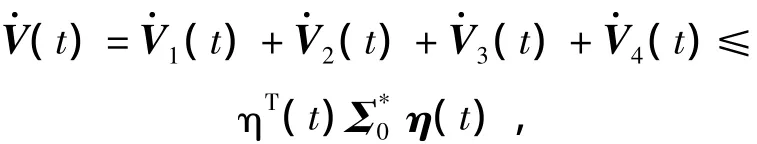
where

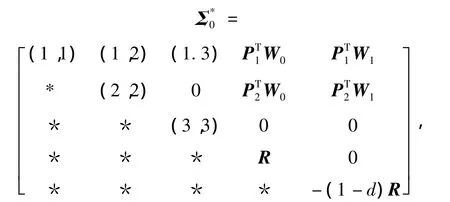
where

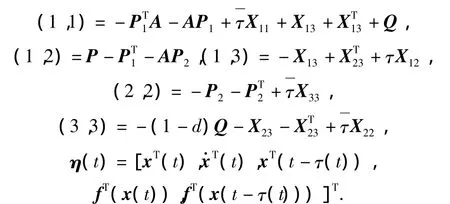
It should be noted that，for any diagonal matrices S ＞0 and T ＞0，from Eq.(6)we have，

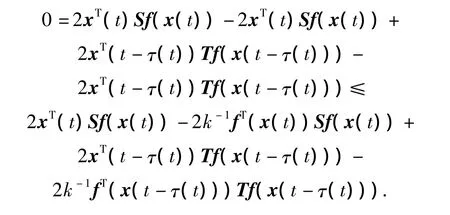
The above inequality is added to(t)to have(t)≤ηT(t)Σ0η(t)＜0.From Lyapunov-Krasov-skii stability theorem，the System(7)is asymptotically stable.

From theorem 1，the following theorem can be given for the asymptotic stability System(5)with uncertainties satisfying Eq.(2)－(3).

Theorem 2If there exist the real matrices P1，P2，X12，X13，X23，the symmetric positive definite matrices P，Q，R，X11，X22，X33，the diagonal matrices S ＞0，T ＞0 and the scalars εi＞0，i=1，2，3 such that Eq.(9)and the following LMI hold:

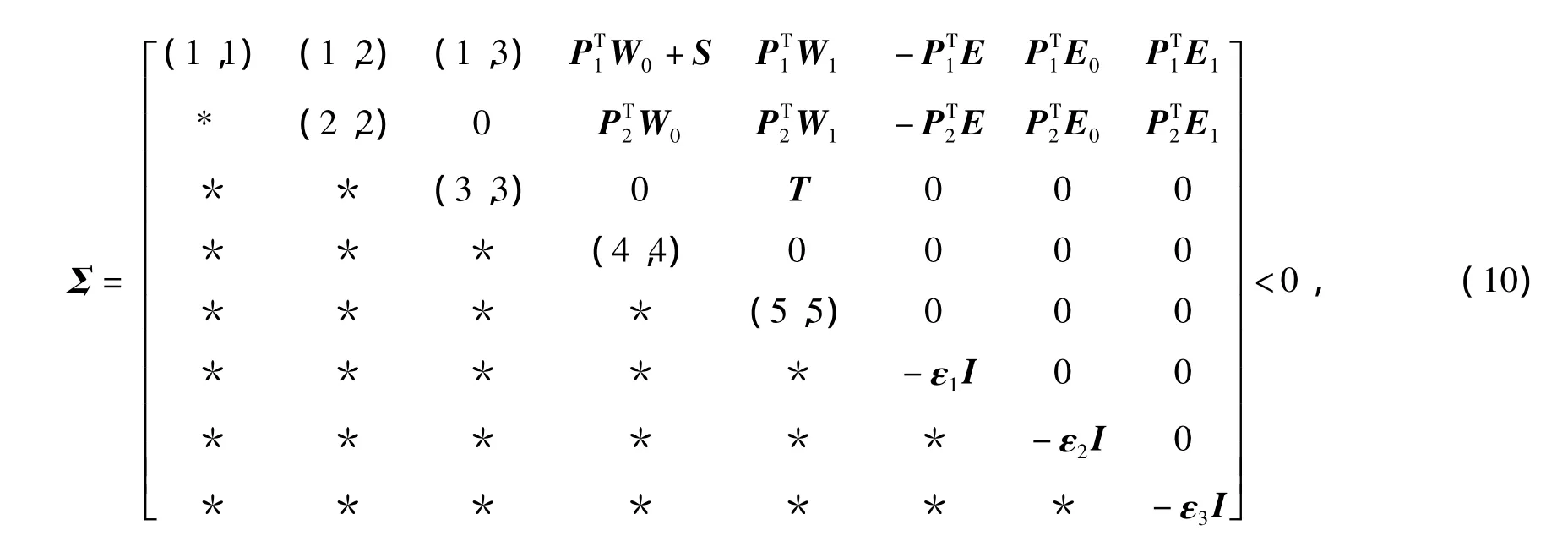
where

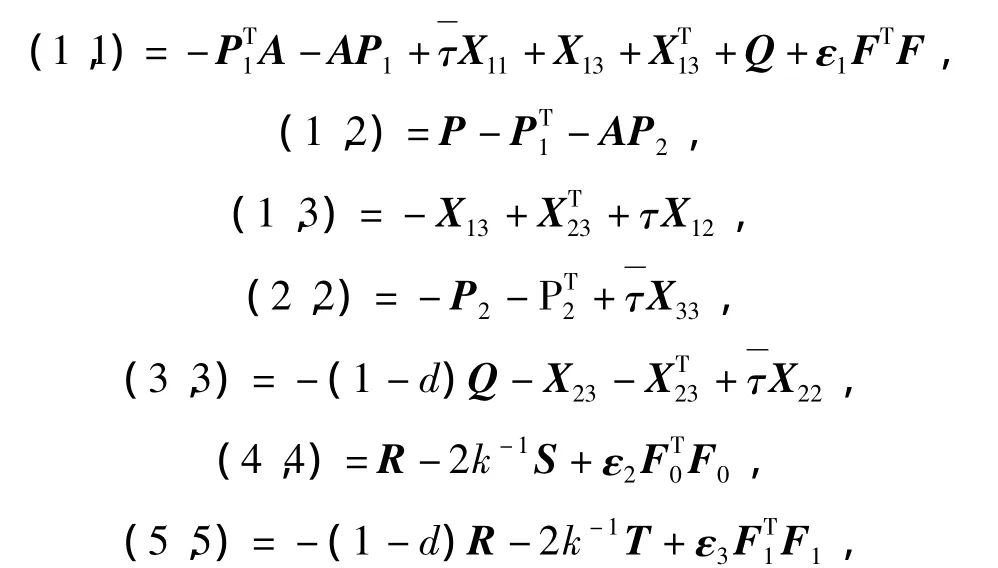
then System(5)with uncertainties satisfying Eq.(2)－(3)is asymptotically stable.

ProofThe desired result can be obtained by multiplying the left and the right hand sides of Eq.(10)by vectors ξT(t)and ξ(t)，respectively，where

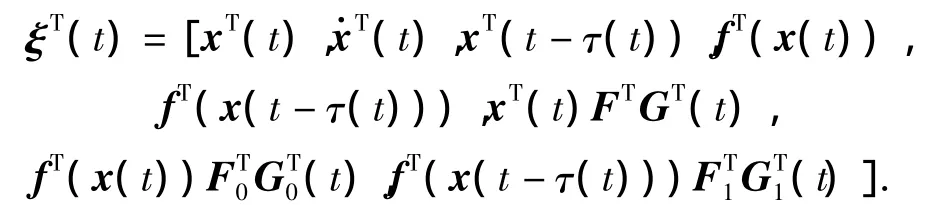
Remark 1In Ref.［4，6－9］，(t)≤d＜1 needs to be met，and in Ref.［5］，this constraint was removed，but the derived criterion is independent on the derivative of time-varying delay function.Obviously，our results are delay-dependent and include the information of the derivative of time-varying delay function.

3 Numerical Example

In this section，we use an example to illustrate the effectiveness of our results.

ExampleConsider the following neural networks with time-varying delay in Ref.［5］

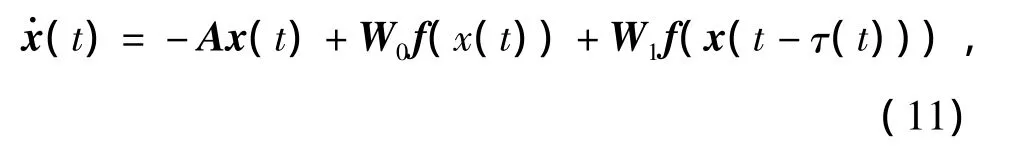
where

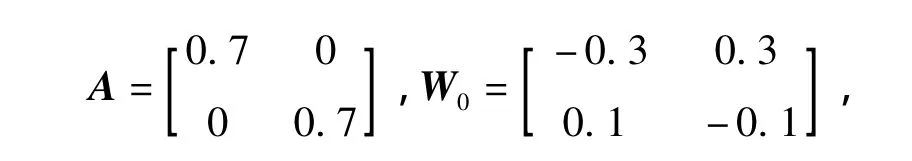
W1=［|x+1|－ |x－1|］/2，and k=1.

By comparing theorem 1 in Ref.［5］to theorem 1 in this paper，we can find that the former is a delayderivative-independent one，i.e.，the criteria in Ref.［5］is true for any d;for d=2，by solving Eq.(8)and(9)from theorem 1 in this paper，we can conclude that System(11)is asymptotically stable and the maximal admissible time delay is τmax=3，which is much bigger than=0.291 56 in Ref.［5］.

4 Conclusions

This paper studied the problem of robust stability for neural networks with norm-bounded uncertainties.The time-varying delay function in this paper may be not continuously differentiable，and its derivative may be not smaller than one.Sufficient conditions were presented to guarantee the robust stability of the uncertain neural networks in terms of linear matrix inequalities.A numerical example was given to illustrate that our results are much less conservative than those presented in other references.

［1］Singh V.New global robust stability results for delayed cellular neural networks based on norm-bounded uncertainties［J］.Chaos，Solitions and Fractals，2006，30(5):1165－1171.

［2］Singh V.A novel global robust stability criterion for neural networks with delay［J］.Physics Letters A，2005，337:369－373.

［3］Singh V.Robust stability of cellular neural networks with delay:linear matrix inequality approach［C］∥IEE Proc-Contr Theor Appl，IEE-INST Elec Eng，Hertford Press，2004，125－129.

［4］ZHANG H，LI C，LIAO X.A note on the robust stability of neural networks with time delay［J］.Chaos，Solitons and Fractals，2005，25(2):357 －360.

［5］YANG H，CHU T，ZHANG C.Exponential stability of neural networks with variable delays via LMI approach［J］.Chaos，Solitons and Fractals，2006，30(1):133－139.

［6］LIAO X，LI C.An LMI approach to asymptotical stability of multi-delayed neural networks［J］.Physica D，Elsevier Science，2005，200:139－155.