潛艇操縱性水動力數值計算中湍流模式的比較與運用

柏鐵朝 梁中剛 周軼美 敬 軍

中國艦船研究設計中心，湖北 武 漢 430064

潛艇操縱性水動力數值計算中湍流模式的比較與運用

柏鐵朝 梁中剛 周軼美 敬 軍

中國艦船研究設計中心，湖北 武 漢 430064

湍流模式的選取對潛艇操縱性水動力數值計算精度有著重要影響，采用六種湍流模式計算了SUBOFF主艇體及主艇體加指揮室圍殼兩種模型在一定漂角范圍內的潛艇操縱性水動力，并與試驗值進行了比較，結果表明SST k-ω模型更為適合潛艇操縱性水動力計算。在此基礎上對SUBOFF全附體模型在一定漂角和攻角范圍內的艇體水動力進行預報計算，并對該計算方法應用于潛艇操縱性水動力預報計算的計算精度與適用范圍進行了探討。

潛艇操縱性；水動力；湍流模式

1 引 言

潛艇操縱性是潛艇綜合航行性能中非常關鍵的技術之一，良好的操縱性對于潛艇的戰斗力、工作效能、安全性、經濟性都有非常重要的意義［1］。潛艇操縱性研究的關鍵技術之一是確定水動力導數，而潛艇的水動力導數種類多達一百多項，有位置導數、角速度導數、舵角導數、以及復雜的耦合導數等。正是由于其復雜性，目前工程上還只能依賴縮比模型試驗來獲取潛艇水動力導數，但是這種方式顯然存在一些缺點，比如：試驗周期長、經費開支大、存在尺度效應和試驗誤差、原理性不強和受試驗場地限制等。20世紀90年代以來，隨著計算機技術的發展，運用CFD技術數值求解潛艇操縱性水動力與力矩成為可能并得到了運用［2－4］。潛艇操縱運動時外流場的典型特點是在翼面與主艇體的背流區域存在分離流現象且分離流隨著來流攻角的增大更為明顯。對于存在分離流的流場模擬，湍流模式是影響計算精度的關鍵因素之一。湍流模式的相關研究至今已經開展了100多年，可是目前仍然沒有一種普遍適用的湍流模式，對于湍流模式的的分析評價一直是近幾十年來流體力學的研究熱點，即使是對已經存在并已獲得廣泛運用的湍流模式也缺乏公認的評價［5，6］。很多情況下，湍流模型的選取要考慮到研究者經驗、流場流動的特點、計算精度與計算能力后方可決定。

為比較目前在CFD計算中獲得廣泛運用的5種二方程湍流模式及RSM湍流模式對潛艇操縱性運動時繞流場模擬的準確性，本文首先采用這些模式對SUBOFF兩種簡單模型在一定漂角范圍內的水動力與力矩進行計算，將計算值與實驗值進行比較，得出了更適用于潛艇操縱性水動力數值計算的湍流模型。在此基礎上計算了全附體SUBOFF潛艇模型在一定攻角和漂角下的水動力與力矩，并討論了該數值計算方法用于潛艇操縱性水動力預報的計算精度與適用范圍。

2 湍流模型的比較與選取

在進行分析計算時，將相關參考及坐標定義為：L——主艇體長；Lpp——艇體垂線間長；LF——艇體進流段長；Lp——艇體平行中體長；LA——艇體去流段長；D——艇體最大直徑；xcg——艇體重心至艇艏距；H——指揮室圍殼高；LS——指揮室圍殼長；B——指揮室圍殼最大寬度；Ls－f——指揮室圍殼前緣至艇艏距離；l——尾翼展長；bb——尾翼底部弦長；bt——尾翼端面弦長；lf－f——尾翼后緣至艇艏距離；U——來流速度；X——縱向力；Y——橫向力；Z——垂向力；K——橫傾力矩；M——縱傾力矩；N——轉艏力矩

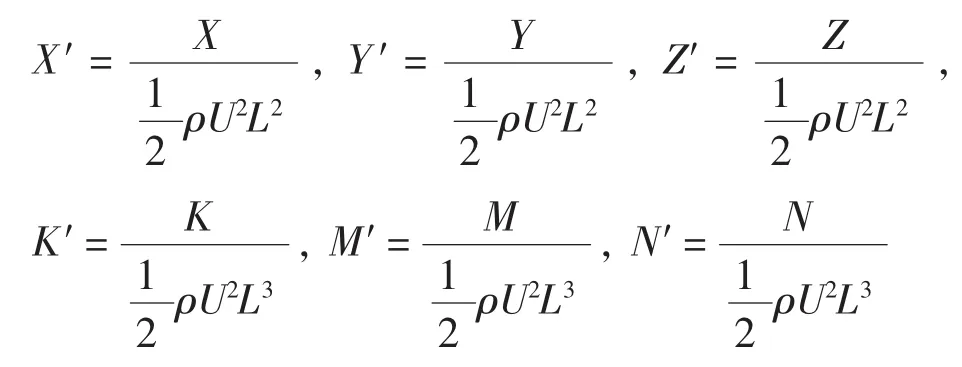
文中設定縱舯剖面與基面的交線為x軸 （橫坐標），向艇艉為正方向；舯截面與基面的交線為y軸 （縱坐標）；縱中剖面與舯截面的交線為z軸（豎坐標），向上為正方向，向右舷為正方向。原點為艇艏端點。

2.1 計算模型的選取

本文選用SUBOFF主艇體（圖1）和SUBOFF主艇體加指揮室圍殼（圖2）兩種模型作為計算對象，其原因有以下兩點：其一，潛艇操縱運動時，作用在主艇體上的水動力是潛艇總水動力的主要組成部分，且主艇體的繞流場是典型的三維分離流動，所以主艇體水動力計算的準確度將直接影響到全附體潛艇水動力的計算精度；其二，主艇體加指揮室圍殼模型是典型的潛艇主／附體連接形式，對研究潛艇操縱性水動力數值計算方法具有直接的指導意義。模型的主要參數如表1所示。

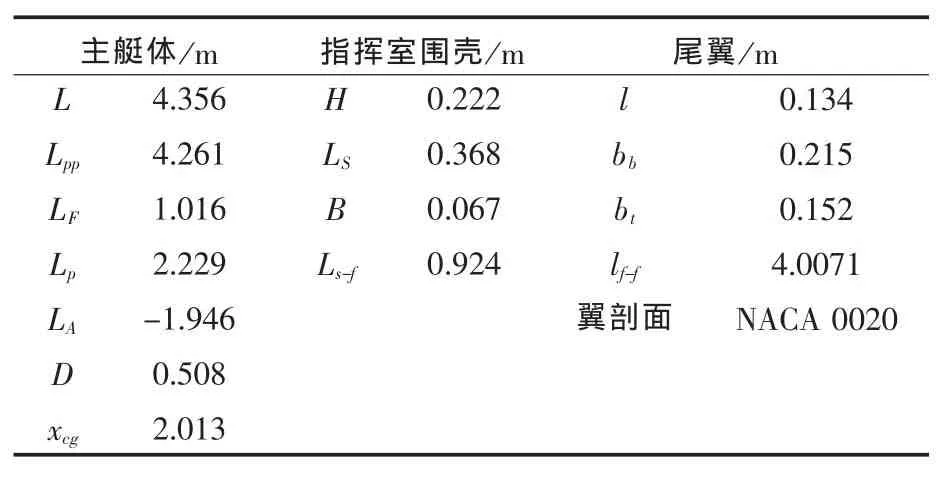
表1 SUBOFF模型主要參數

2.2 計算流域、網格劃分及邊界條件設定

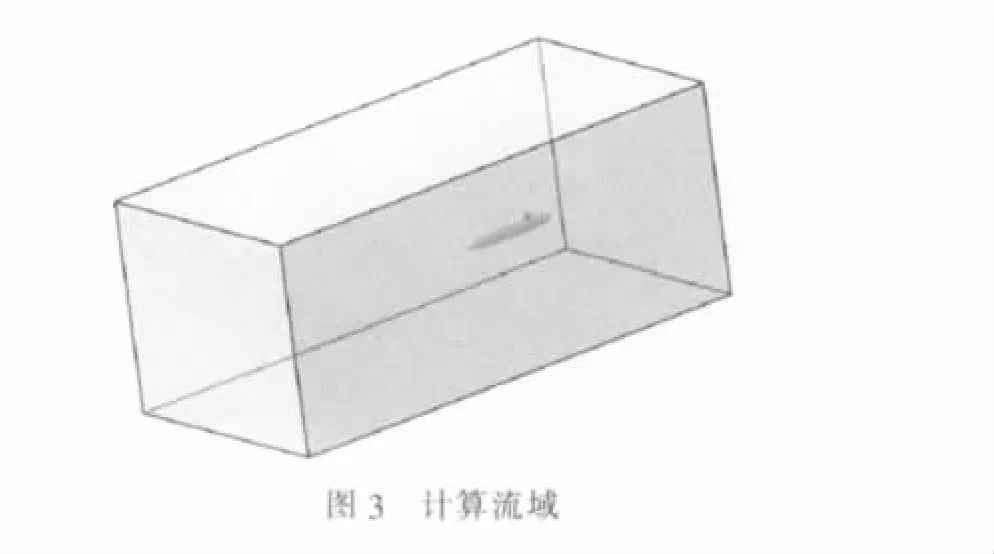
2.2.1 計算流域

計算流域為一長方體區域（圖3），L為艇體長度，其邊界范圍為：

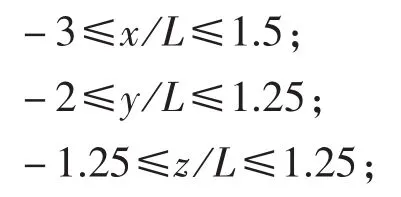
2.2.2 網格劃分

采用ICEM CFD軟件劃分網格，為提高計算精度整個流域采用全結構網格布置。其中，主艇體與主艇體加指揮室圍殼模型的網格數分別為114萬和162萬。

2.2.3 邊界條件設定

1） 進口處為速度進口邊界條件，u＝3.341 m／s，入口處湍流參數根據相關文獻［7］給定。

2）出口為壓力出口邊界條件。

3）上下面為對稱邊界條件。

4）艇體表面為壁面無滑移邊界條件。

5）k－ε與RSM模型在近壁區采用壁面函數法，k－ω模型采用近壁模擬法。

2.3 湍流模式與數值計算方法

文中對二方程湍流模式中的Standard k－ε模式、RNG k－ε 模式、Realizable k－ε 模式、Standard k－ω模式、SST k－ω模式及RSM湍流模式進行分析比較，各湍流模式的數學表達及特點可參照相關文獻［6］，［7］。計算采用直接求解三維粘性不可壓RANS方程的方法，使用有限體積法對微分方程進行離散，擴散項使用中心差分格式，對流項采用二階迎風格式，流場計算采用SIMPLEC算法。

2.4 計算結果及分析

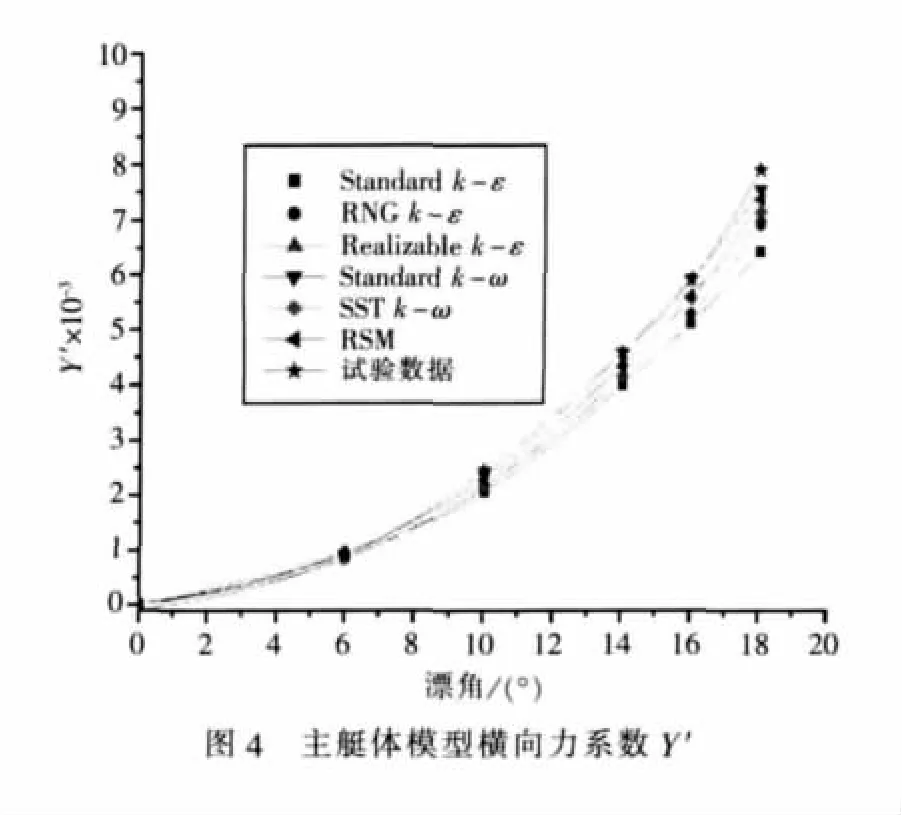
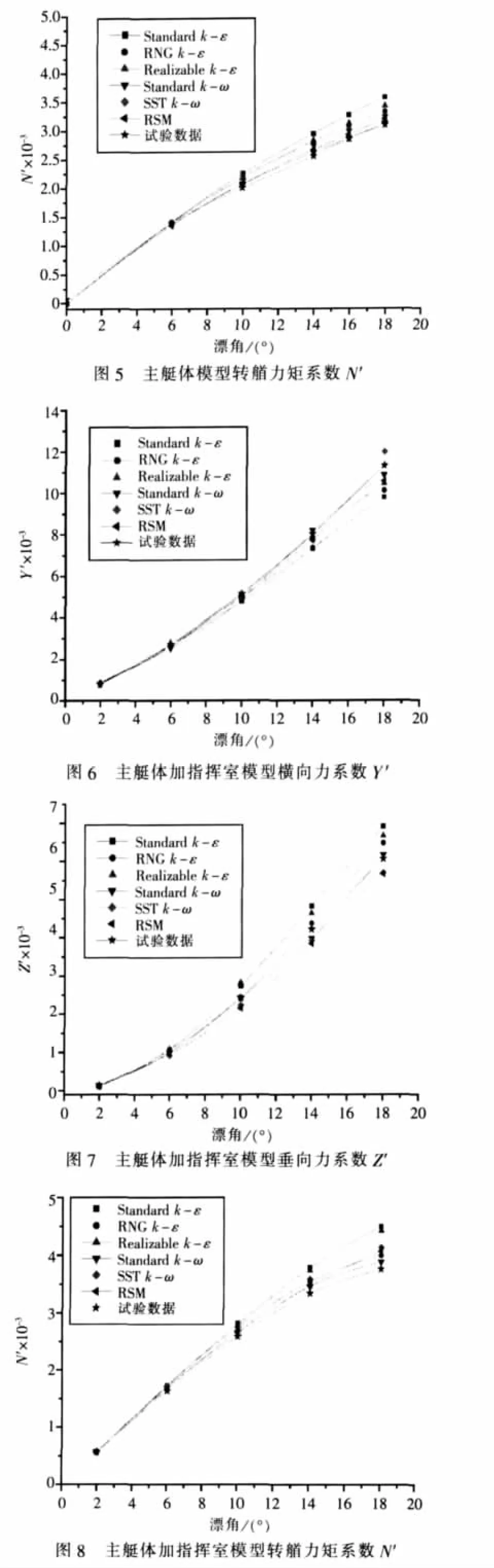
運用FLUENT軟件求解流場，得到在漂角β?（0°～18°）范圍內主艇體模型橫向力系數 Y′、轉艏力矩系數N′（圖4～5）與主艇體加指揮室模型的橫向力系數Y′、垂向力系數Z′及轉艏力矩系數N′（圖6～ 圖 9），并將其與文獻［8］中的試驗結果比較。

計算結果表明：在小角度范圍內（β≤10°）文中運用的6種湍流模式計算得到的水動力與力矩與試驗值均非常接近。隨著漂角的繼續增大，計算值的誤差均隨之增大，且不同湍流模式的精度亦有較大差別（表2～表3）。其中，運用RSM與k－ω模式得到的結果與試驗值更為接近，而Standard k－ε模式的誤差相對較大。其原因主要有：

1）隨著漂角增大分離流的強度也在加強，RANS湍流模式均不能很好地處理大攻角下的分離流計算。

2）湍流模型對計算結果有著重要影響，主要體現在Reynolds應力項的處理方式及各模型在近壁區的處理方法。

對于Reynolds應力項的處理，k－ε與k－ω模型均基于Boussinesq粘渦假定，屬于各向同性湍流模式，但在近壁湍流及彎曲壁面流動中的雷諾應力具有明顯的各向異性。而RSM模型是基于雷諾應力轉化模型，考慮了一些各向異性效應，所以計算精度應優于二方程模型。

對于近壁區的處理方法，在FLUENT軟件中主要有壁面函數法及近壁模擬法。k－ε模式與RSM模式屬于高Re數的湍流計算模型，而近壁區的流動仍屬于低Re數流動，所以其近壁處理通常借助于壁面函數，但壁面函數法的表達式主要根據簡單的平行流邊界層的實測資料歸納得出，不能“真實”地反映近壁區內流動狀態，而且當流動為彎曲壁面流動或流動分離過大時，這種處理方法不太理想［9］。 而k－ω 模式在近壁處采用Wilcox k－ω近壁模擬，考慮了低Re數效應，能準確地模擬近壁區的流動狀況，且具有較好的數值穩定性。需要指出的是Wilcox k－ω近壁模擬模型對近壁區的網格稠密度要求較高。由于操縱性計算中關注的力與力矩的計算精度主要與近壁區內壓力計算精度有關。從這個角度來看，k－ω模式的計算精度要優于k－ε、RSM模式。

為進一步開展分析，本文比較了漂角β＝18°狀態下的幾種模式的計算差異。比較圖4～圖8可知，指揮室圍殼對潛艇操縱性水動力性能影響顯著，以β＝18°狀態下轉艏力矩系數N′作為分析對象，針對靠近主艇體的一個指揮室圍殼剖面（Z＝－0.27 m），比較了運用 RSM、SST k－ω 與 Standard k－ε湍流模式的計算壓力分布。在指揮室圍殼迎流面三種湍流模式的計算結果非常一致，如圖9～圖10所示。在背流面出現較大范圍的分離流（圖11）時，采用RSM、SST k－ω模式計算出的表壓分布一致，而Standard k－ε模式與二者有較大差別，主要是在分離區域內壓力值低于運用RSM、SST k－ω模式得到的壓力值，這是運用Standard k－ε模式計算得到的N′值偏大的原因之一。

綜合以上分析可知：在小漂角范圍內，針對這兩種計算模型，文中運用的二方程湍流模式與RSM模型均有較高的計算精度，在較大漂角下，RSM模式、k－ω模式的計算精度要優于k－ε模式，其中Standard k－ε模式誤差較大，而改進后的RNG k－ε、Realizable k－ε模式在計算精度與數值穩定性上均優于Standard k－ε模式。值得注意的是，RSM模式雖然考慮了一些各項異性效應，但本文的計算表明，在潛艇模型處于較大的來流攻角下并沒有顯出其明顯的數值穩定性與計算精度優勢，且RSM模式的計算時間要比二方程模型多耗費40%左右。而SST k－ω模式在近壁處采用Wilcox k－ω近壁模擬，在邊界層邊緣和自由剪切層采用k－ε模式的k－ω形式，其間通過一個混合函數來過渡，這樣消除了k－ω模式的原型對自由來流湍流度的極強依賴性，使其對自由來流的湍流度也不敏感。本文計算亦表明宜采用SST kω模式做為潛艇操縱性水動力數值計算的湍流模式。

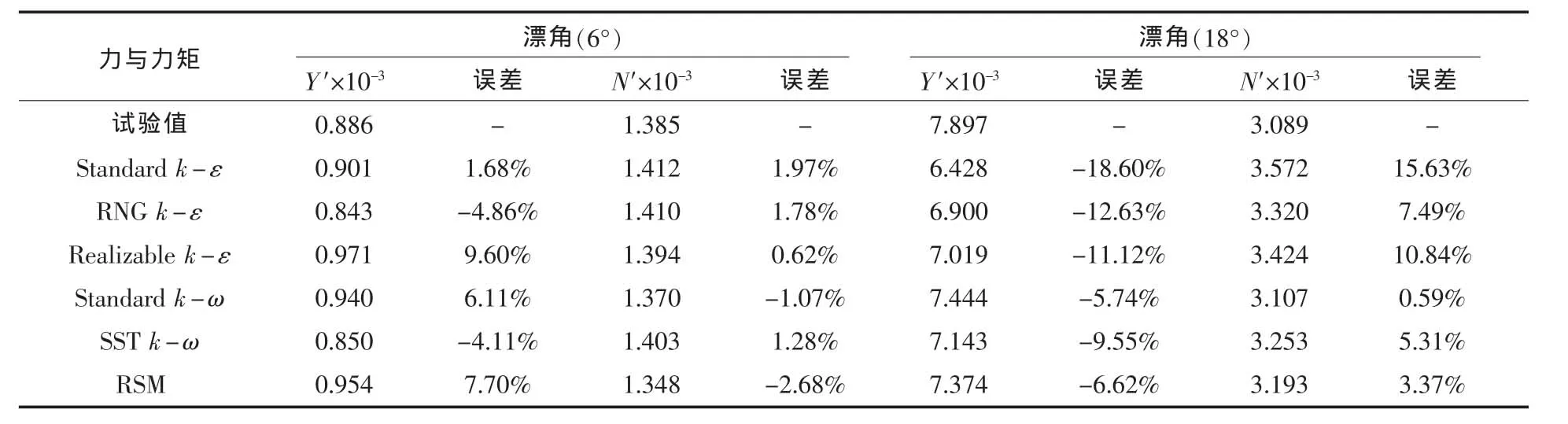
表2 主艇體模型橫向力系數、轉艏力矩系數計算結果

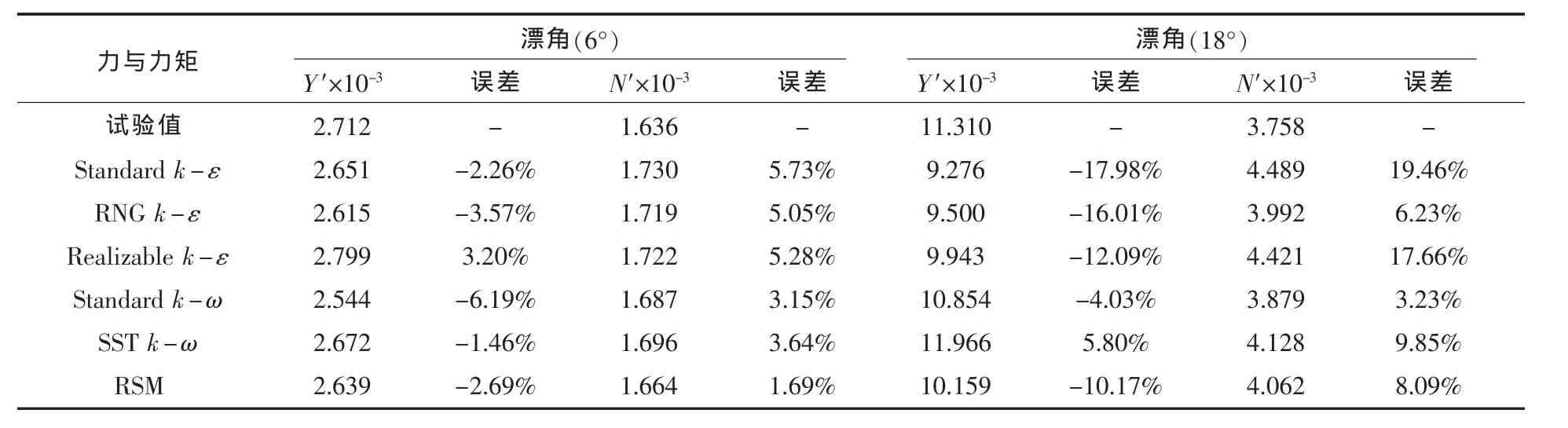
表3 主艇體加指揮室圍殼模型橫向力系數、轉艏力矩系數計算結果

3 全附體潛艇模型操縱性繞流場數值計算

前面針對主艇體及主艇體加指揮室圍殼模型的操縱性水動力性能進行了計算，計算結果與試驗值較吻合。為進一步探究該方法對潛艇操縱性水動力的預報能力，作者針對SUBOFF全附體模型（圖 12）在較大攻角 α?（－16°～16°）和漂角 β?（0°～14°）范圍內的潛艇操縱性水動力性能進行了計算。如圖13～圖20所示，計算結果表明：

1） 在攻角 α ?（－16°～16°） 內， Realizable kε、SST k－ω兩種湍流模式的計算值與試驗值的比較符合預期規律，其中SST k－ω模式的計算值更為接近試驗值。在小攻角（≤10°）范圍內計算值與試驗值非常接近（誤差在7%以內）。

2） 在漂角 β?（0°～14°）內，采用 SST k－ω 模式的計算結果基本與試驗值一致，但相對于模型在有攻角下的計算結果誤差較大。其重要原因在于處于斜流之中的指揮室圍殼對操縱性水動力有很大影響，而由此引發的背流區流動分離及主附體間的干擾作用對數值計算精度有著不小的挑戰。需要指出的是，在漂角β＝0°時，文中引用的水池試驗數據中K′、N′、Z′值均與零點有較大差別，這表明試驗數據本身也存在一定的誤差，但比較試驗水動力導數與通過線形回歸 β?（0°～4°）內的計算值所得的水動力導數可知兩者基本一致，如表4所示，這也表明了數值計算運用于求解潛艇操縱性水動力系數的準確性。

3） 考慮到模型在有攻角 α?（－16°～16°）的其余4個分力變化均不明顯，限于篇幅本文未列出。對比本文3個模型在攻角與漂角下的計算結果可知：指揮室圍殼對水平面潛艇操縱性能有著至關重要的影響，潛艇回轉過程中伴隨的橫傾、縱傾和潛浮運動均與指揮室圍殼的外型與位置有著緊密的聯系，因此基于潛艇操縱性考慮的艇體指揮室圍殼外型優化的是非常必要的。

4）隨著攻角和漂角角度的增加，計算值誤差增大較為明顯，與工程許可的誤差限定亦有較大差距。影響大角度下計算精度的關鍵還是在于各種湍流計算模式對流動分離的模擬能力。對于存在大規模的分離湍流流場，RANS模型的計算精度有限。

表 4 中，Yν′， Kν′，Nν′試驗值為試驗報告直接給出，而水動力導數的計算值及 Zν′，Mν′試驗值為作者通過最小二乘法線性回歸 β?（0°～4°）時計算數據與試驗數據所得。

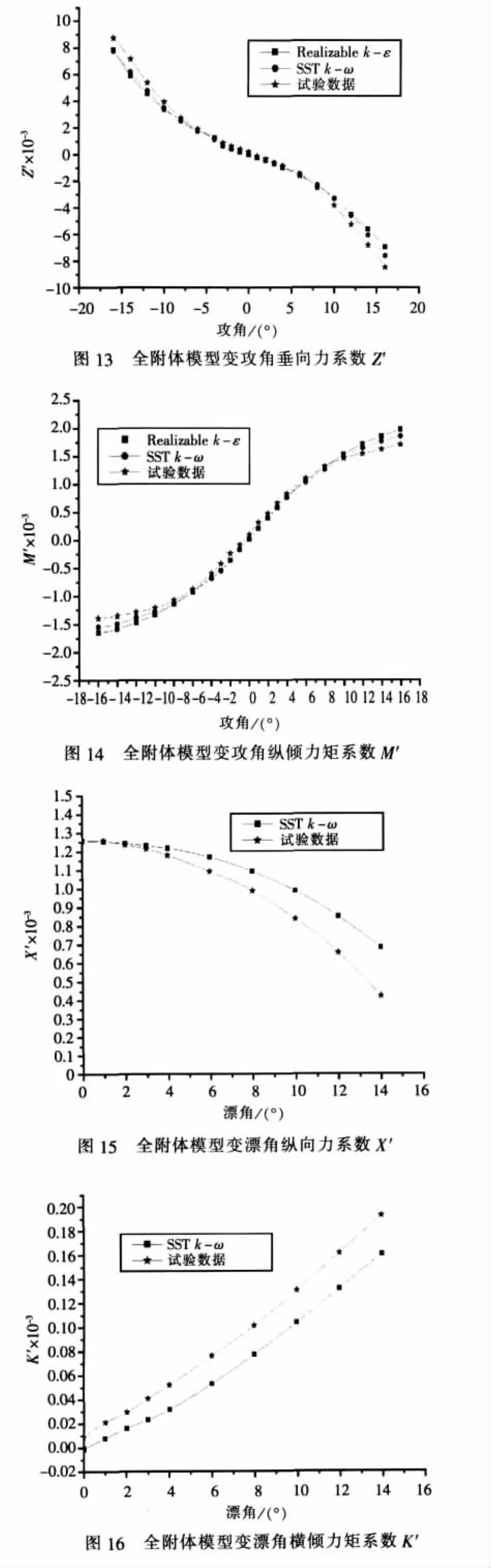
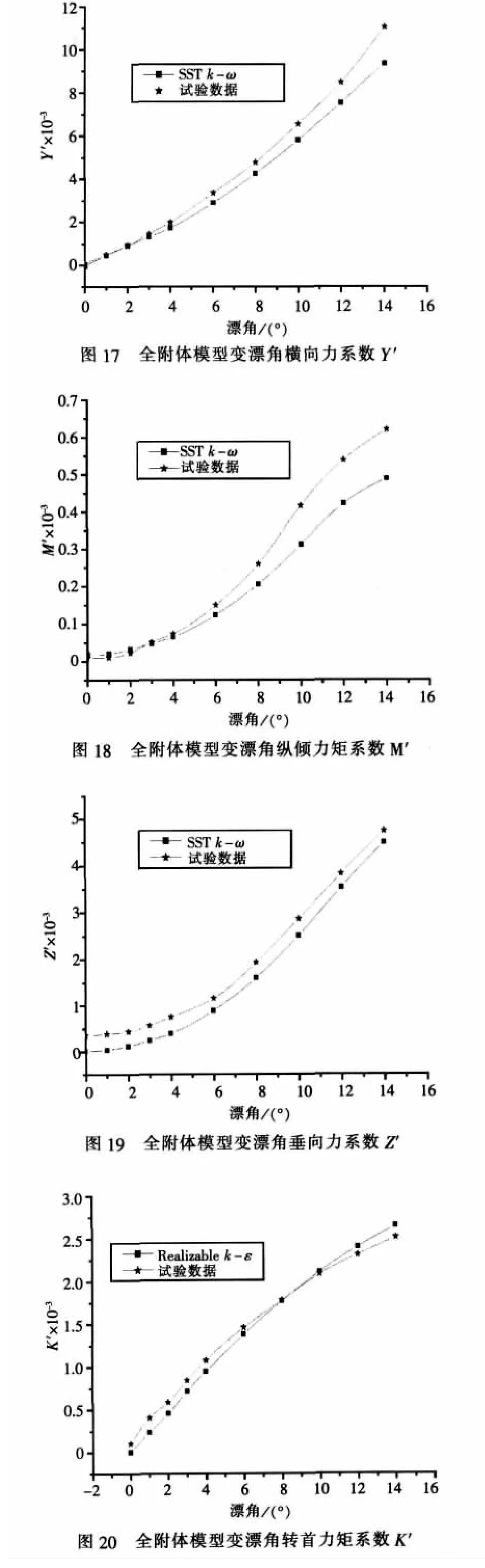
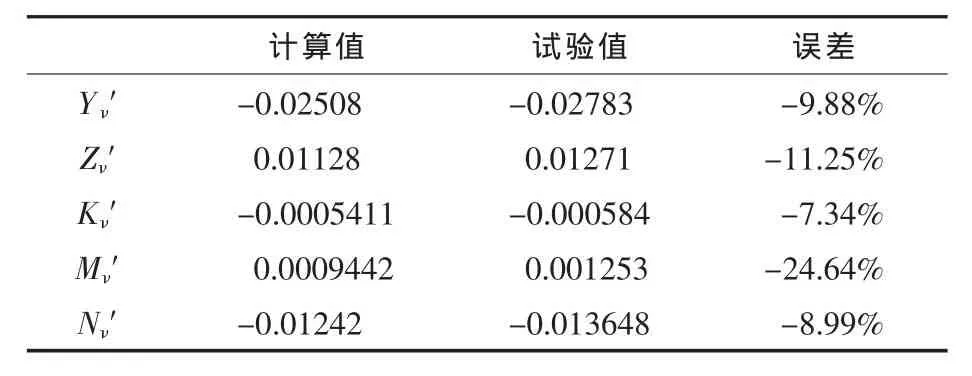
表4 水動力導數對照表

4 結 論

本文詳細比較了6種RANS湍流模式對SUBOFF主艇體及主艇體加指揮室圍殼模型的操縱性水動力計算精度的影響，得出了較為適合潛艇操縱性水動力計算的湍流模式，在此基礎上對全附體SUBOFF模型在有攻角和漂角下的六分力進行了計算，并對該計算方法運用于潛艇操縱性水動力預報計算的計算精度與適用范圍進行了有益的探討，初步討論了指揮室圍殼對潛艇操縱性能的影響。主要結論如下：

1）對于潛艇操縱性水動力數值計算，k－ω模式及RSM模式的計算精度要優于k－ε模式，其中運用Standard k－ε模式得到的計算誤差較大。考慮到計算精度與計算時間，SST k－ω湍流模型更為適合進行潛艇操縱性水動力數值計算。當然，必須要注意的是k－ω采用的近壁模擬方法對近壁區網格稠密度要求比壁面函數法要高。

3）計算表明指揮室圍殼對潛艇水平面的操縱性能影響較大，在潛艇水平面變漂角過程中，艇體所受的垂向力、橫滾力矩及俯仰力矩均有較大變化，這些力與力矩對潛艇轉向和回轉過程中的艇體姿態控制非常重要。因此，開展基于潛艇操縱性能考慮潛艇指揮室圍殼外型優化的研究非常必要。

［1］陳厚泰.潛艇操縱性［M］.北京：國防工業出版社，1981.

［2］TAYLOR L K，PANKAJAKSHAN R M，JIANG C S.Large-scale simulations for maneuvering submarines and propulsors ［C］//AIAA 29th Plasmadynamics and Lasers Conference， 1998.AIAA.98-2930.

［3］ZHENG X，LIAO C，LIU C.Multigrid multi-block computation of incompressible flows using two-equation turbulent models ［C］//AIAA 35th Aerospace Sciences Meeting and Exhibit，1997.AIAA.97-0626.

［4］潘子英，吳寶山，沈泓萃.CFD在潛艇操縱性水動力工程預報中的應用研究［J］.船舶力學，2004，8（5）：42-51.

［5］WILCOX D C， LA C?NADA.Turbulence modeling： an overview［C］//AIAA 39th Aerospace Sciences Meeting and Exhibit， 2001.AIAA.2001-0724.

［6］張兆順，崔桂香，許春曉，等.湍流理論與模擬［M］.北京：清華大學出版社，2005.

［7］Fluent Inc.FLUENT User’s Guide［S］.Fluent Inc.2003

［8］RODDY R F.Investigation of the stability and control characteristics of several configurations of the DARPA SUBOFF model［R］.Departmental Report，Ship Hydromechanics Department，David Taylor Research Center，1990.

［9］王福軍.計算流體動力學分析［M］.北京：清華大學出版社，2004.

Comparison and Application of Turbulence Modes in Submarine Maneuvering Hydrodynamic Forces Computation

Bai Tie－chao Liang Zhong－gang Zhou Yi－mei Jing Jun
China Ship Development and Design Center，Wuhan 430064，China

The selection of turbulence mode plays an important role in the accurate numerical simulation of a submarine maneuvering hydrodynamic forces.In this paper，computations with six different turbulence modes were performed for the two configurations of the SUBOFF model，one was an axisymmetric hull and the other was hull with sail.Compared with experimental data，the results for varying drift angles，indicate that SST k－ω turbulence model is more suitable for submarine maneuvering hydrodynamic forces computation.Then，computation and prediction of the maneuvering hydrodynamic forces for SUBOFF model with full appendages were processed by varying attack angles and drift angles.The accuracy and applicability of the present method for predictive computation of submarine maneuvering hydrodynamic forces were also discussed.

submarine maneuverability； hydrodynamic force； turbulence mode

U661.1

A

1673－3185（2010）02－22－07

2009－05－06

柏鐵朝（1984－），男，碩士研究生。研究方向：船舶水動力數值計算研究。E-mail：baitiechao＠qq.com

梁中剛（1966－），男，研究員，碩士生導師。研究方向：船舶總體研究設計