基于歐拉梁理論的管路縱向波功率流簡化模型誤差分析

劉 彥 周進華

中國艦船研究設計中心，湖北 武 漢 430064

基于歐拉梁理論的管路縱向波功率流簡化模型誤差分析

劉 彥 周進華

中國艦船研究設計中心，湖北 武 漢 430064

為分析基于歐拉梁理論的管路縱向波功率流簡化模型的誤差，首先基于殼體理論推導了充液管路縱向波功率流的精確模型，該模型解析和表述了管路材料、幾何參數以及管內液體流速等因素與功率流之間的關系，通過與基于歐拉梁理論的功率流簡化模型的對比即可得到簡化模型的誤差。理論分析與仿真結果表明：在低頻區(qū)，基于歐拉梁理論的縱向波功率流模型誤差近似為一恒定的常數，該常數與厚徑比以及管路的材質有關，而管路半徑以及管內流速對簡化模型誤差的影響可以忽略。

管路；功率流；簡化模型；誤差分析

1 引言

管路作為輸送水、油、蒸汽的主要載體在化工、核電、船舶等領域發(fā)揮重要的作用，然而在其發(fā)揮主要功能同時也成為不必要振動和噪聲的傳輸載體，嚴重影響了周圍環(huán)境，甚至會因振動造成管路損壞而帶來安全隱患。開展管路功率流測試是分析管路振動傳遞特性、控制管路振動的重要手段，因此管路功率流測量研究受到國內外學者的關注［1－4］。

目前對充液管路建模的精確理論無疑是殼體理論，而殼體理論認為管路存在無窮多個徑向模態(tài)，而每個徑向模態(tài)又對應無窮多軸向模態(tài)，盡管經過簡化依然包含較多變量［5－7］， 不利用實際操作。因此，在工程上退而求其次，采用歐拉梁理論對充液管路進行簡化處理，這勢必會帶來一定的誤差，故有必要對該誤差進行理論分析，為功率流測量精度的提高奠定理論基礎。雖然國內外學者對基于歐拉梁理論簡化模型的誤差有過一定的分析［8］，但是這些分析都是定性的、片面的，目前尚沒有對管路特性參數與管內液體流速等因素對簡化模型誤差的確切影響的研究。為了全面分析該誤差，本文首先基于Flügge方程推導了充液管路縱向波功率流的精確模型，通過與工程上使用的基于歐拉梁理論的功率流模型對比，即可分析基于歐拉梁理論的簡化模型的誤差，通過分析得出了簡化模型的應用范圍以及注意事項，為縱向波功率流精確測試提供理論支撐。

2 理論模型

由于工程中使用管路的管壁遠小于其半徑，因此充液管路一般可等效為充液薄壁圓柱殼體，充液薄壁圓柱殼體的自由振動Flügge方程可表示為：

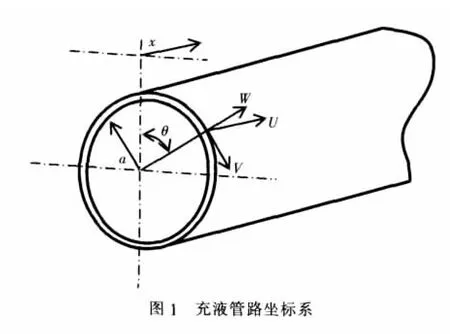
式中，a為殼體中性面半徑；ν為泊松比；E為殼體材料的楊氏彈性模量；ρ為密度；h為壁厚；β2為厚度因子（β2＝h2／12a2）；Δ2是 Laplacian 算子（Δ2＝a（?2／?x2） + ?2／?θ2），U、V、W 分別為中性面上任意一點的軸向、切向和徑向位移；x、r、θ為柱面坐標。具體情況如圖1所示。

依據參考文獻［9］～［11］，U、V、W 以及 P 具有以下的形式：

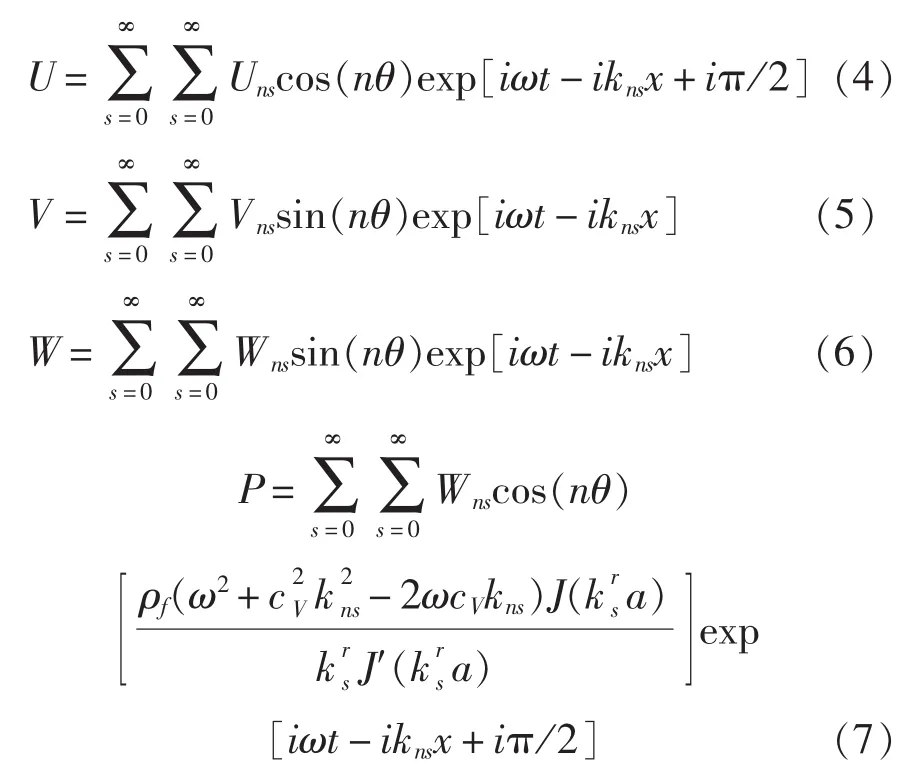
式中，kns為軸向波數；為徑向波數，ρf為管內液體密度；cV為液體流速，J（·）為一階貝塞爾函數。

將式（4）～式（7）代入式（1）～式（3）整理后可得充液管路系統的耦合模型的矩陣形式。

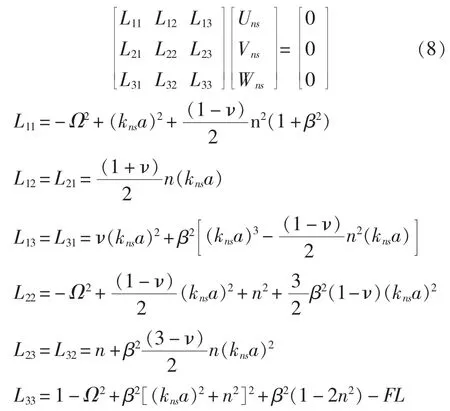
式中，Ω＝ωa／cL為無量綱頻率；cL液體中的聲速；FL為流固耦合項。

而流固耦合項可以用貝塞爾函數表示為：

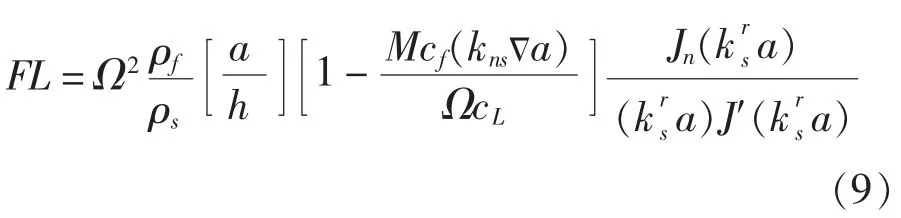
式中， M＝cV／cf為馬赫數。

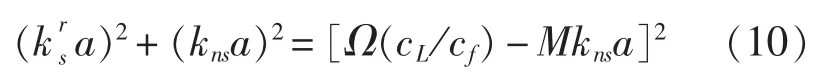
依據式（8）可得殼體中性面上的任一點三向位移之間的關系：

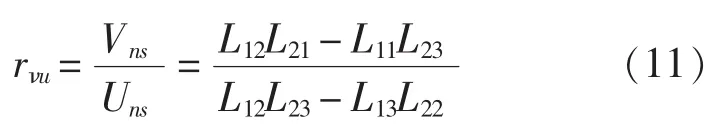
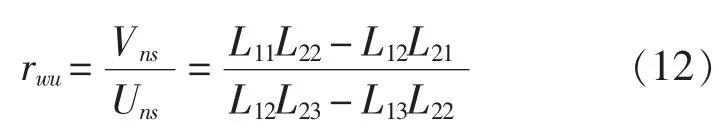
基于殼體理論的縱向波功率流可以表示為：

式中，〈A，B〉為 A和B的互譜；Nx為軸向力。

而殼體總軸向力可以表示為：

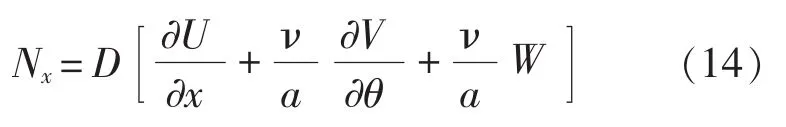
式中， D 為膜剛度，D＝Eh（1－ν2）

將式（14）帶入式（13）整理后可得功率流表達式。

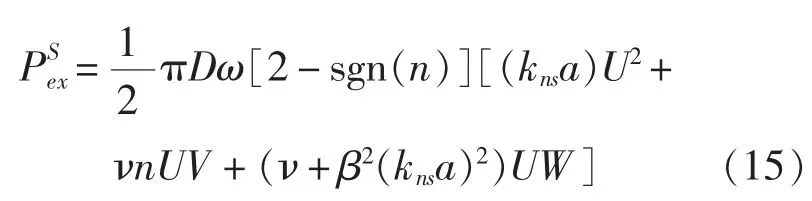
由于不同軸向模態(tài)之間沒有能量交換，因此對于任意模態(tài)（n，s）有：

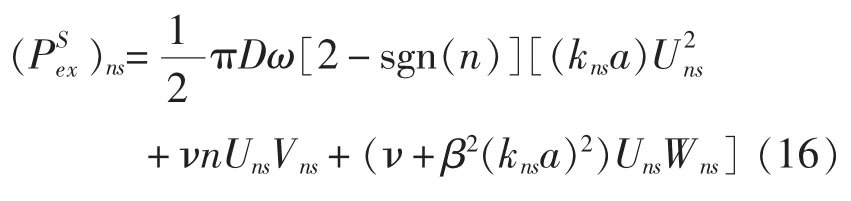
為了便于工程應用，往往利用梁模型理論對管路進行簡化。依據歐拉梁理論，梁內僅存在相互解耦的縱向波、扭轉波和彎曲波，而縱向波功率流可以表示為：

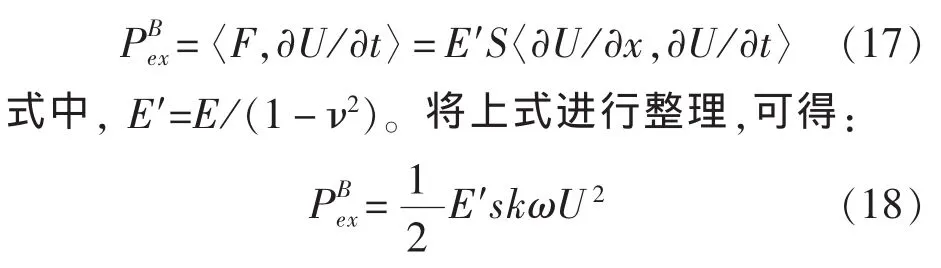
式中的k為波數，雖然基于歐拉梁理論獲得的波數與基于殼體理論獲得的波數具有一定的差別，但在工程測試時，無論用那種方法測量縱向波功率流，所用波數都是同一實測結果。因此，此處的波數k可以直接利用殼體理論所獲得的kns代替。

在頻率低于殼體一階環(huán)頻率時，殼體內可以傳遞能量的傳輸波只有n＝0時對應的扭轉波（s＝0）、縱向波（s＝2）和 n＝1 時的彎曲波［9］，此時將式（16）和式（18）相除，并將式（11）和式（12）帶入可得：

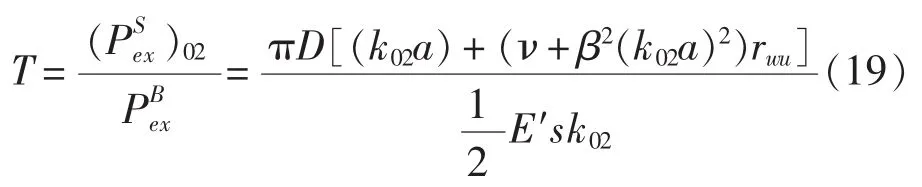
首先利用式（8）～式（10）求出沿管路傳遞的縱向波的波數 k02，然后結合式（11）～式（12）可以獲得任一點三向位移之間的比值，將這些參數帶入式（19）即可求得基于兩種不同理論的縱向波功率流之比，而通過分析這一比值就可以得到基于歐拉梁理論縱向波功率流簡化模型誤差的變化規(guī)律。

3 數值仿真與分析

在工程實際中，應用最多的管材是不銹鋼和硬橡膠，它們的基本參數如表1所示。下面就以這兩種材料為研究對象，分析不同條件下的縱向波功率流簡化模型的誤差。

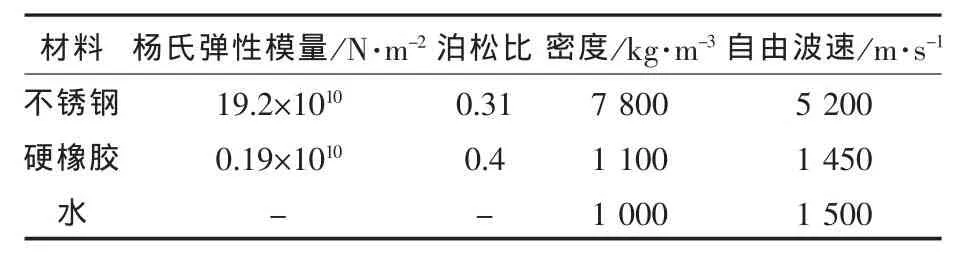
表1 材料的特性參數

首先分析不同厚徑比（h／a）對功率流簡化模型誤差的影響。利用上一節(jié)推導的公式，分別求出h／a＝0.1、0.05 和 0.005 條件下， 兩種模型所獲得功率流比值隨無量綱頻率的變化情況，結果如圖2所示。

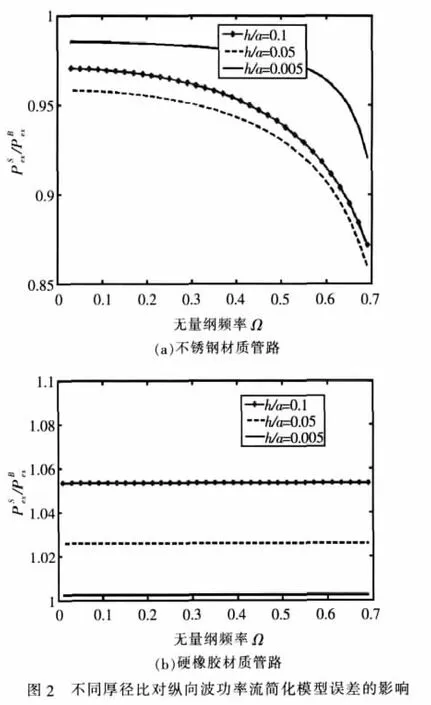
由圖2（a）可見，對于不銹鋼材質管路而言，基于梁理論的簡化模型獲得功率流要大于基于殼體理論的精確值。隨著厚徑比的減小，功率流簡化模型誤差變化不是單調的，而是先變大然后再減小；而在厚徑比相同的情況下，功率流簡化模型誤差都是隨著無量綱頻率的增加而增加。在所分析頻段內誤差保持在15%以內，而在無量綱頻率0.3以下，誤差隨著頻率變化很小，近似為常數。依據圖2（b）可知，與不銹鋼材質的管路相反，對于硬橡膠材質的管路而言，基于梁理論的簡化模型獲得功率流要小于基于殼體理論的精確值。隨著厚徑比的減小，功率流簡化模型誤差呈現單調遞減的趨勢。值得注意的是，在厚徑比相同的情況下，簡化模型的功率流誤差在整個分析頻段內基本保持恒定而與頻率無關，因此在無量綱頻率0.7以下，對簡化模型的功率流進行簡單修正就可以獲得相應的精確值。

工程中應用的管道半徑多為 0.01～0.1 m，對鐵質管路而言，無量綱頻率0.3對應的頻率是25～2.5 kHz，對于硬橡膠材質管路而言，無量綱頻率 0.7 對應的頻率是16 ～1.6 kHz，而工程實際中所關心的頻段主要集中在1 kHz以下。因此在工程實際中，可以直接使用基于歐拉梁理論的簡化模型測量功率流，然后乘以一個修正系數就可以獲得對應的精確值，這個系數與管路材質以及厚徑比有關。

其次分析相同厚徑比（h／a），不同半徑對功率流簡化模型誤差的影響。對于厚徑比比較小的薄壁管路而言，管路橫截面積s≈2πah，帶入式（19），整理后得：

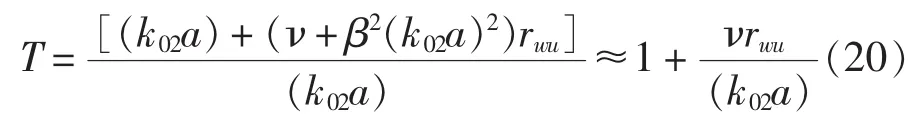
由上一節(jié)的推導過程可知，管路系統的無量綱縱向波數k02a與無量綱頻率Ω的關系受厚徑比影響，而與半徑無關，因此由式（20）可知，在厚徑比相同且以無量綱頻率Ω作為橫坐標的前提下，半徑的變化對功率流簡化模型誤差沒有影響。需要注意的是，半徑的變化會造成實際頻率ω發(fā)生變化，因此在以實際頻率作為橫坐標的條件下，圖2所示的一條曲線將變成一簇曲線，但變化趨勢以及誤差的最大值將不會發(fā)生變化。

最后，分析管內流速變化對功率流簡化模型誤差的影響。同樣以不銹鋼材質和硬橡膠材質的管路為研究對象，分別分析 h／a＝0.05，流速 v＝5 m／s、20 m／s、40 m／s情況下， 兩種模型所獲得功率流比值隨無量綱頻率的變化情況，所得結果如圖3所示。

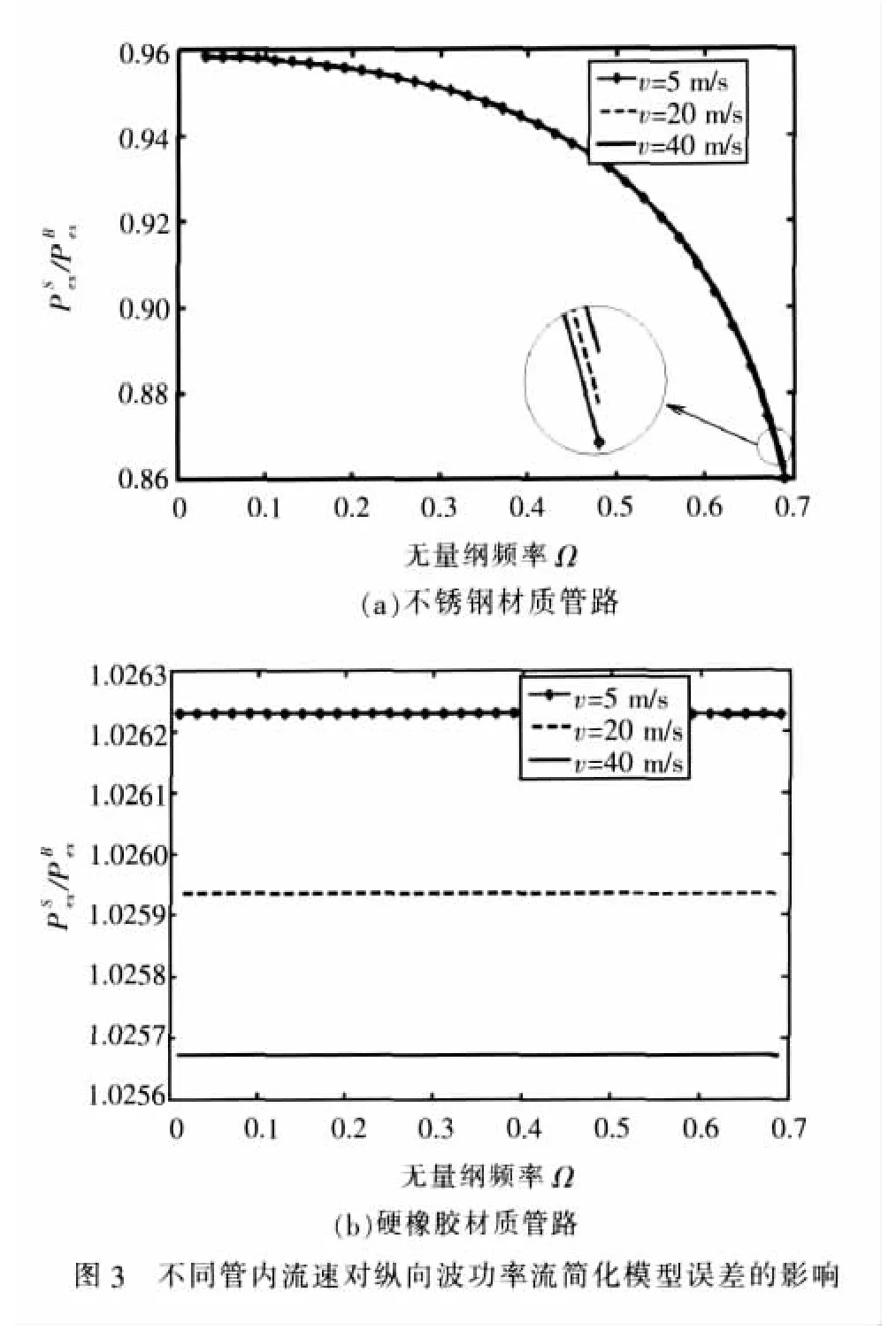
由于水中的聲速v為1 500 m／s，因此所分析的3種流速條件下，對應馬赫數都遠小于1，對管路系統的縱向波數基本不產生影響，因此無論對于不銹鋼管路還是硬橡膠管路系統，流速的變化對功率流比值影響都不大，亦即對簡化模型的誤差影響較小。在工程實際中管路中的流速通常小于5 m／s，因此流速的影響可以忽略不計。需要注意的是，這個結論是在無限長直管模型下獲得的，因此只在長直管道成立，而在管路的彎管、變徑等不連續(xù)位置處并不成立。

4 結論

本文分別基于殼體理論和歐拉梁理論建立了充液管路的縱向波功率流模型，并利用兩者的比值定量分析了基于歐拉梁模型的縱向波功率流簡化模型的誤差隨厚徑比、半徑以及管內液體流速的變化發(fā)生變化的情況，得到以下結論：

1）基于歐拉梁理論的縱向波功率流簡化模型的誤差隨著管路材質與厚徑比的變化而變化，對于鐵質管路而言，基于歐拉梁理論測得的縱向波功率流將偏大，而對于硬橡膠材質管路則偏小，但在低頻區(qū)，兩種材質的管路都可直接使用基于歐拉梁理論的簡化模型測量功率流，然后乘以一個修正系數即可獲得對應的精確值，這個系數與管路材質以及厚徑比有關。

2）對于相同的厚徑比，縱向波功率流簡化模型的誤差隨無量綱頻率的變化情況與半徑無關。

3）由于工程實際中管內流體馬赫數遠小于1，因而對較長的直管段進行縱向波功率流測量時，管內均勻流速的影響可忽略。

［1］PAVIC G.Vibration energy flow in elastic circular cylindrical shells［J］.Journal of sound and vibration，1990，142（2）：193－310.

［2］朱顯明，張國良，黃其柏，等.均勻流管自由振動的能量分布特征［J］.振動、測試與診斷，1999，19（2）：95－99.

［3］THIEN A B，CHIAMORI H C，CHING J T，et al.The use of macro－fibre composites for pipeline structural health assessment ［J］.Structural control and health monitoring，2008，15（1）：43－63.

［4］KARAGIOZIS K N，AMABILI M，PAIDOUSSIS M P，et al.Nonlinear vibrations of fluid－filled clamped circular cylindrical shells ［J］.Journal of Fluids and Structures，2005，21：579－595.

［5］BREAVART B J， FULLER C R.Radial impusive excitation of infinite fluid －filled elastic cylindrical shells ［J］.Journal of sound and vibration， 1994， 177（3）： 411－422.

［6］XU M B.Three methods for analyzing forced vibration of a fluid－filled cylindrical shell［J］.Applied Acoustics，2003，64： 731－752.

［7］徐慕冰，張小銘，張維衡.充液圓柱殼中的振動能量流［J］.華中理工大學學報，1997，25（2）： 85－87.

［8］FINNVEDEN S.Simplified equations of motion for the radial－axial vibrations of fluid filled pipes ［J］.Journal of sound and vibration， 1997， 208（5）：685－703.

［9］FULLER C R，FATHY F J.Characteristics of wave propagation and energy distributions in cylindrical elastic shells filled with fluid ［J］.Journal of sound and vibration，1982，81（4）： 501－518.

［10］BREAVART B J，FULLER C R.Effect of an internal flow on the distribution of vibrational energy in an infinite fluid－filled thin cylindrical elastic shell ［J］.Journal of sound and Vibration， 1993， 167（1）： 149－163.

［11］朱顯明，朱英富，張國良.殼式管道管壁振動能量流的測量方法［J］.中國造船，2004，45（4）：29－34.

Error Analysis of Simplified Model Based on Euler Beam Theory for Power Flow of Longitudinal Waves in Pipes

Liu Yan Zhou Jin－h(huán)ua
China Ship Development and Design Center， Wuhan 430064，China

In order to analyse the error of simplified model based on Euler beam theory for power flow of longitudinal waves in pipes， the exact model was developed firstly.based on shell theory， which shows the relationship among materials of pipes， geometrical parameters， internal flow velocity and power flow.Then the error of simplified model based on Euler beam theory can be obtained by comparing the simplified model with the exact model.Theory analysis and simulation results show that in low frequencies，the error of the simplified model is approximately a constant， which is determined by thickness－radius ratio and materials of pipes，and the effect of the radius and internal flow velocity on the error can be neglected.

piping system；power flow；simplified model；error analysis

TB532

A

1673－3185（2010）02－13－05

2009－05-06

劉 彥（1979－ ），男，博士，工程師。 研究方向：噪聲振動控制。E-mail：liuyanhit＠gmail.com