教學離高考有多遠?
——談在新課標教學中落實知識、過程和方法

邊 良

(潞河中學 北京 通州 101149)

1 兩道高考題

在2009年的高考中，上海和北京的物理高考題不約而同的各考了一道關于電場強度的疊加問題．兩道高考題如下

1．1 上海高考題

兩帶電荷分別為q和-q的點電荷放在x軸上，相距為L，能正確反映兩電荷連線上場強大小E與x關系的是圖1中的

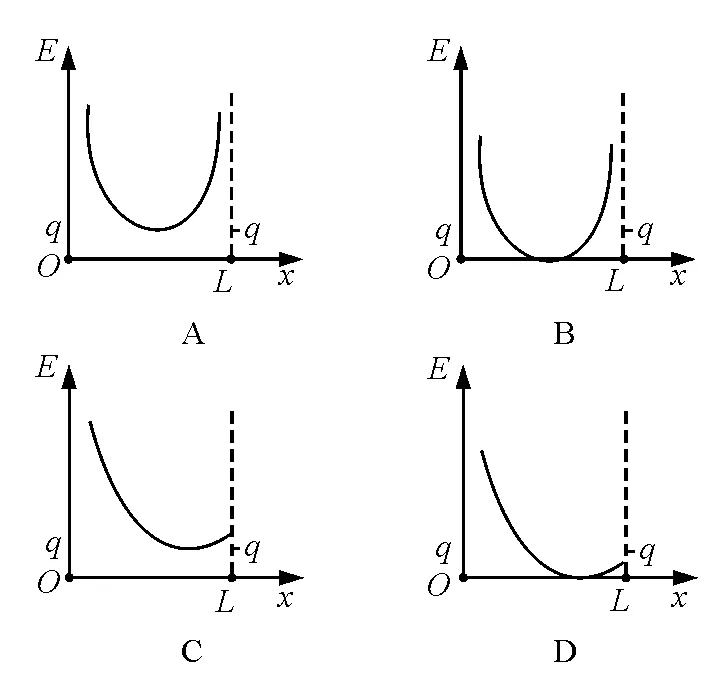
圖1

1．2 北京高考題

圖2所示為一個內、外半徑分別為R1和R2的圓環狀均勻帶電平面，其單位面積帶電荷為σ．取環面中心O為原點，以垂直于環面的軸線為x軸．設軸上任意點P到O點的的距離為x，P點電場強度的大小為E．下面給出E的四個表達式(式中k為靜電力常量)，其中只有一個是合理的．你可能不會求解此處的場強E，但是你可以通過一定的物理分析，對下列表達式的合理性做出判斷．根據你的判斷，E的合理表達式應為

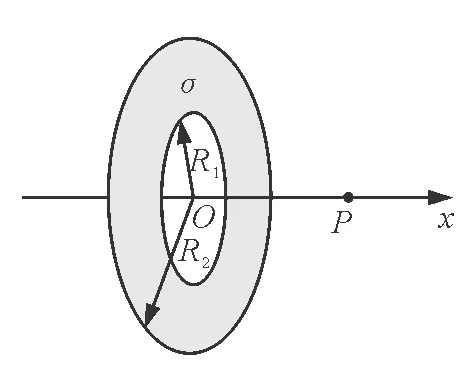
圖2

電場強度疊加的計算是物理教學中的一個常規問題，但是在實行新課標教學的今天，對這個問題應該怎樣教，應該怎樣考，值得研究．2009年上海和北京的這兩道高考題令人耳目一新．兩道題形式新穎，題目設計別具一格，給出了新課標下這個問題的新的考法，即不但要考查關于場強疊加的知識，而且要考查計算場強疊加的物理、數學方法，還要考查關于場強疊加的知識形成過程．應該說，這兩道題的設計很好的體現了新課標關于突出知識、方法和過程的教學理念，是非常成功的考題．

從學生答題的反映看，認為這兩道題比較難．其實這兩道題對應的物理教學元素分別是一對等量異號點電荷、一對等量同號點電荷電場的場強疊加問題．如果學生在解答這個問題時不能聯系這方面所學的知識，說明我們關于場強疊加的教學不到位，說明學生對場強疊加的方法掌握不夠靈活．

2 在場強的疊加教學中落實新課標的要求

下面是筆者關于等量點電荷場強疊加的教學過程，教學設計思想是，試圖讓學生在掌握關于場強疊加知識的同時，突出知識的形成過程，學會關于場強疊加的分析方法．

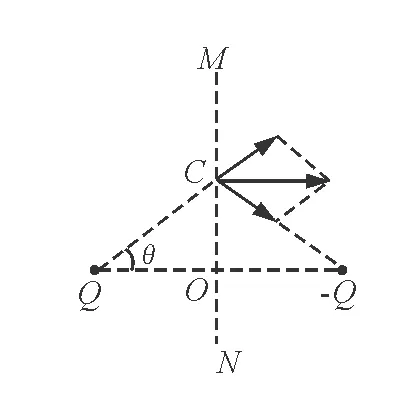
圖3

【例1】一對等量異號點電荷，所帶電荷量分別為Q和-Q，放在相距L的兩點，O是它們連線的中點，MN是兩個點電荷連線的中垂線，如圖3所示．試比較：

(1)沿中垂線，從O到無窮遠處場強的變化情況；

(2)沿兩個點電荷連線，從Q到-Q場強的變化情況．

教學過程：

問題1：中垂線上一點C處的場強是誰產生的？(從問題入手思考)

畫出C點的場強．畫出O點的場強．(掌握疊加方法)

比較沿中垂線，從O到無窮遠處場強方向有什么特點？場強度大小怎樣變化？說出你的依據．

方法1：電場線法.(疏密，略)

方法2：疊加法．根據點電荷的場強公式

可知，距離O點越遠，每個點電荷在該點產生的場強越小；而根據場強疊加可知，距離O點越遠，兩個點電荷產生的場強夾角越大．這兩個因素使得距離O點越遠合場強越小；在無窮遠處，r→∞，兩個點電荷產生的場強為零，合場強為零．

結論：從O到無窮遠處，場強方向與中垂線垂直并指向負電荷一方；電場強度大小逐漸減小，在無窮遠處場強為零．

問題2：你能夠寫出中垂線上某點的合場強表達式進行分析嗎？(運用數學方法從定性到定量)

分析：設中垂線上該點距離O點為x，則合場強

問題3：以O為原點，沿中垂線向上為x軸正向，你能夠畫出中垂線上的E-x圖線嗎？(建立數、形關系)

畫圖線依據為

1)根據上述函數關系可知，E-x圖線是曲線；

做出圖線如圖4所示．

圖4

問題4：沿兩個點電荷連線，從+Q到-Q，場強的大小怎樣變化？你能寫出某點的場強表達式進行分析嗎？(習慣訓練)

方法1：電場線法．(疏密，略)

方法2：疊加法．+Q和-Q之間的距離為L，設沿兩個點電荷連線上有一點C，距離+Q為x；則C點的場強為

利用這個公式進行推理(外推法)

2)從兩個點電荷向中點O看，電場強度逐漸減小(對稱法).

問題5：以+Q為原點，以+Q和-Q連線并指向-Q為x軸正向，你能夠畫出兩個電荷連線上的

E-x圖線嗎？(建立數、形關系)

畫圖線依據：

1)根據上述函數關系可知，E-x圖線是曲線；

做出圖線如圖5所示.

圖5

根據上面5個問題的解決，歸納為等量異號點電荷連線中點的場強，是兩電荷連線上的場強的最小值，是兩電荷連線中垂線上場強的最大值．

對教學過程的評價：兩個等量異號點電荷連線上和中垂線上的場強變化情況，用電場線的疏密也可以進行定性分析，但是這樣分析比較淺顯.如果教學只滿足于此，學生得到的是結論，并沒有掌握場強疊加的具體方法．按照新課標的要求，把這個問題的教學從定性轉化為定量，一方面是讓學生對場強疊加的過程有明確的認識，掌握知識的形成過程，進行過程教學；另一方面，通過過程教學，展現場強疊加的各種方法，包括物理方法和數學方法．這樣，在這個問題的教學中就體現了知識、過程和方法，培養了學生的能力和習慣，而這正是新課標的教學要求．這時，再看一下2009年的上海高考題，學生就會有“一覽眾山小”的感覺．

下面用同樣的方法討論一對等量同號點電荷的場強迭加情況.

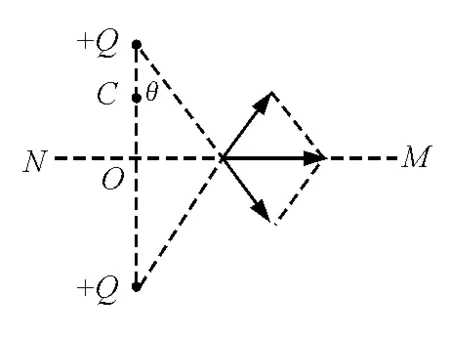
圖6

【例2】一對等量同號點電荷，所帶電荷量均為+Q，放在相距L的兩點，O是它們連線的中點，MN是兩個點電荷連線的中垂線(圖6).試比較：

(1)沿中垂線，從O到無窮遠處場強的變化情況；

(2)沿兩個點電荷連線，從+Q到+Q場強的變化情況．

問題1：做出中垂線上一點和兩個電荷連線中點的場強(掌握疊加方法)．沿中垂線，從O到無窮遠處場強方向有什么特點？場強大小怎樣變化？說出你的依據．(學會比較方法)

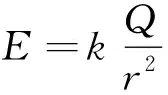
問題2：你能夠寫出中垂線上某點的合場強表達式嗎？(數學方法的運用)

分析：設中垂線上該點距離O點為x，則合場強為

根據這個表達式，利用數學方法可以計算場強最大值的位置和最大值，有興趣的同學課下不妨推導一下．(為物理學習好的同學留有余地)

問題3：沿兩個點電荷連線，場強的大小如何變化？你能寫出某點的表達式進行分析嗎？(習慣訓練)

兩電荷之間的距離為L，設沿兩個點電荷連線上有一點C，距離電荷+Q為x，則C點的場強為

利用上面公式進行推理.

2)從兩個點電荷向它們的連線中點看，電場強度逐漸減小.(對稱法)

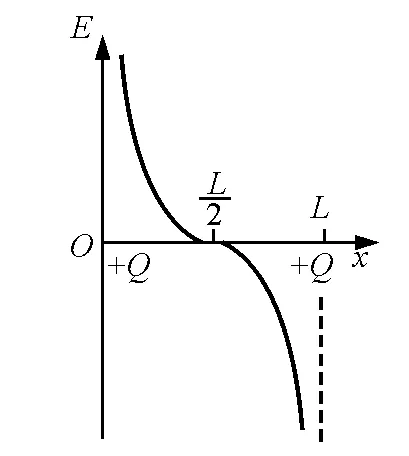
圖7

做出兩個點電荷連線上場強的E-x圖像，如圖7所示．比較可以看出，這與一對等量異號點電荷連線上的場強變化圖像是不同的．

根據上述3個問題的解決，歸納成等量同號點電荷連線中點的場強，是兩電荷連線上場強的最小值，是兩電荷連線中垂線上場強的最小值．

下面做拓展分析.

圖8

問題4：如果在一個正方形的4個頂點各放一個等量的正點電荷，如圖8所示.在正方形的中心O處的場強多大？沿著過中心O并垂直于正方形平面的軸線從O到無窮遠處的場強怎樣變化？

分析方法：

疊加法.各點的場強是4個電荷電場疊加形成的．

對稱法.兩個對角線上的一對電荷在O點產生的場強為零，在a點產生的場強不為零，在無窮遠點產生的場強為零；根據場強疊加，4個正點電荷在中心O和無窮遠處的合場強均為零，比較兩個電荷疊加的結果推理：沿著過中心O并垂直于正方形平面的軸線從O到無窮遠處的場強是先變大后變小．

圖9 均勻帶正電圓環

問題5：如果有一個均勻帶正電的圓環，如圖9所示.在圓環中心O處的場強多大？在過中心O并垂直于圓環平面的軸線上從O點到無窮遠處的場強怎樣變化？

分析方法：

微元法.圓環看做無數個帶正電的點電荷組成.

對稱法.圓環每一條直徑兩端的的兩個等量同號點電荷在圓環中心O處的疊加場強為零，在a點產生的場強不為零，在無窮遠點產生的場強為零；根據場強疊加，整個圓環上的電荷在中心O和無窮遠處的產生的合場強均為零，沿著過中心O的軸線從O到無窮遠處的場強是先變大后變小．

問題6：如果有一個均勻帶正電的薄圓盤，如圖10所示，在圓盤中心O處的場強多大？在過中心O并垂直于圓盤平面的軸線上從O點到無窮遠處的場強怎樣變化？

圖10 均勻帶正電圓盤

分析方法：

微元法.帶電圓盤看作無數個帶電線段(直徑)或圓環組成；每條帶電線段或圓環看做無數個帶正電的點電荷組成.

對稱法.每條帶電直徑上相對圓心對稱的兩個帶正電的點電荷在圓盤中心O處產生的場強為零，在a點產生的場強不為零，在無窮遠點產生的場強為零；根據場強疊加，整個圓盤上的電荷在中心O和無窮遠處的合場強均為零，沿著過中心O的軸線從O到無窮遠處的場強是先變大后變小．

問題7：如果有一個均勻帶正電的圓球，從圓球的中心到無窮遠處的場強怎樣變化？有興趣的同學可以課下思考．(為物理學習好的同學留有余地)

3 高考對教學的啟示

我們知道，解決電場疊加問題，在大學物理中用到的典型方法就是微元法和對稱法．可以說，關于一對等量同號點電荷產生的電場疊加，經過這樣的變化訓練后，學生會得到從感性到理性的綜合提高，會掌握知識的形成過程和方法的訓練過程，會使中學物理所學的知識、方法延伸到大學物理，并且提出了多個值得思考和解決的問題，使學生對這個問題的學習感到余味無窮．

我們再看前面提到的2009年北京的高考題：解該題用到的方法有對稱法、微元法和疊加法(量綱法和排除法也可以應用)．選擇正確答案要知道兩個事實：第一，在x=0處場強E=0；第二，在x→∞時場強E→0，然后把所給表達式適當變換，就可以得到正確結果，這又用到了數學方法和外推法．可以說，這道題考的是關于電場疊加從基礎到提高的一系列知識，體現的是物理方法和數學方法的綜合運用，反映的是學生學習過程和教師的教學過程對知識、方法的落實情況，在這個知識點上全面考查了知識、過程和方法，因此我們說它是一道體現新課標精神的好題．然而，學生在解答這道題時遇到的困惑，恰恰是不知道上述兩個事實，因此形成判斷困難，這不能不說在這個知識點上的教學是不到位的，對一對等量同號點電荷的電場疊加的延伸分析是不到位的，落實新課標的方法、過程教學是不到位的．

根據新課標的要求，物理教學要重視過程教學．進行過程教學的方法之一，就是問題教學．教師在教學過程中通過不斷的提出問題和解決問題，完成教學過程．在解決一個問題時，又會遇到新的問題，這就為提出下一個問題埋下了伏筆．物理知識是物理教學過程的主體，物理方法是物理教學過程的核心，通過方法掌握知識，通過教學過程落實知識和方法．從這個意義上說，物理教學的任務就是知識的掌握、方法的形成、思維的訓練和能力的提高．而那種首先告訴學生結論，然后做大量習題完成教學的方式，是對過程教學非常淺薄或不正確的理解，必須加以改正．