具有非均勻內熱源的多孔介質中自然對流傳熱傳質的數值研究

李 棟 涂鄭禹 李賢宇 鄧玉美

(天津渤海職業技術學院,天津,300022)

具有非均勻內熱源的多孔介質中自然對流傳熱傳質的數值研究

李 棟 涂鄭禹 李賢宇 鄧玉美

(天津渤海職業技術學院,天津,300022)

采用數值方法分析了具有非均勻分布內熱源的豎直同心套管內多孔介質中的傳熱傳質,內熱源分布系數M較大時,造成流場中心的逆時針環流向中心擠壓。浮力比N由1.5變為-1.5后,流體由順時針流動變為逆時針流動且流體速度加快。Nusselt數在Z=0.7處出現轉折。隨M增大內壁面Nusselt數變化范圍增大,并且轉折點前移。上壁面Sherwood數也呈先增大后減小的趨勢,并且在R=0.9處出現轉折。

多孔介質 自然對流 Nusselt Sherwood

1 引言

具有內熱源的多孔介質中自然對流傳熱傳質過程廣泛應用在許多自然科學和工業工程中[1]。例如換熱器、化工過程和電子系統的冷卻、顆粒堆積床中的放熱化學反應等。不同的研究者對豎直管道中的自然對流傳熱傳質進行了數值和實驗研究。K.C.Leong[2]應用數值方法分析了以沸石為填料的同心套管換熱器,討論了傳熱傳質系數,床層厚度,沸石空隙直徑等影響參數,并考察了生成熱對換熱系統影響。B V Rathish Kumar和Shalini[3]研究了具有曲線邊界的多孔介質封閉體中的非達西自然對流,著重論述了非達西效應對流動的影響,Kladias[4]應用DBF模式,系統地研究了Benard對流,發現對流的促發強烈依賴于流動 Prandtl數、Da數和熱傳導系數。但是對諸如石油熱采和近年頗受重視的井下換熱器[5]以及類似實際工程中常見的具有非均勻內熱源的情況,研究尚不充分,資料仍然十分有限。

本文對具有非均勻內熱源的豎直套管中自然對流傳熱傳質進行了數值分析,重點討論了內熱源對流體流動和傳熱傳質的影響。

2 物理模型與控制方程

研究對象為環隙充滿多孔介質的豎直套管封閉腔體。上表面濃度 C1,下底面濃度 C0,高為 H,半徑為Z。內外壁面存在溫度差,側面不滲質。套管管隙內分布有非均勻熱源,并且在管壁處分布密集,管隙中心分布最為稀薄,即內熱源強度隨徑向變化。物理模型及坐標系如圖1所示。

圖1 物理模型及坐標系

根據Darcy-Brinkman-Forchheimer模型,采用Boussinesq近似,引入流函數^ψ,得到其無因次化控制方程如下:

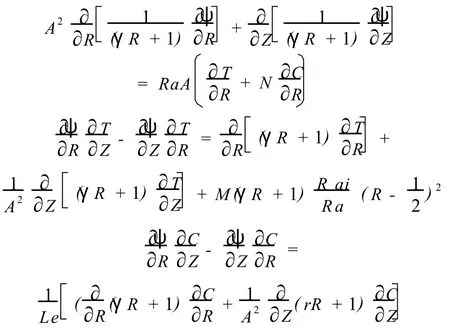
式中,M為內熱源分布系數,表征內熱源強度沿徑向變化的梯度大小。N為反應溫度梯度和濃度梯度相對大小和方向得浮力比,浮力比N反映了物質擴散浮力和熱浮力的耦合關系,當N ＞0時,由溫度梯度產生的熱浮力和由濃度梯度產生的物質擴散浮力方向相同,二浮力作用相互加強,推動流體在封閉體內流動。N＜0時,表明熱浮力和物質擴散浮力方向相反,二浮力相互削弱。

本文研究所用參數為:A=1～20,k=2～10,Ra/Rai=150～1000,N=-5.0～5.0,Le=0.1～5.0,M=0～10。收斂判據為最大相對誤差小于10-5。

3 結果與討論

3.1 與實驗數據的比較

首先在M=0(即無內熱源時),k=5.338,A=1條件下進行了計算。所得數值結果與Deiber[6]實驗值進行了比較。圖2給出了采用Deiber文中定義的局部Nusselt數的實驗結果與數值解的比較。由圖中可以看出,實驗值與數值解吻合較好。

3.2 流線分布

圖3為Rai/Ra=100,k=3,Le=2時不同M,N下的流場的流線分布,圖中ΔΨ=0.6。

圖2 計算值與實驗值比較

圖(a)與圖(b)反映了 A=1,Le=2,k=3,Rai/Ra=100條件下內熱源分布系數M對套管間隙內流體流動的影響。由圖中可以看到隨M增大圖中流線加密并且壁面處的環流區域隨之擴大,說明在非均勻內熱源加熱作用,套管中部流體溫度高于內、外壁面附近流體溫度,造成流場中心的逆時針環流向中心擠壓。同時,內熱源的加熱強度增大造成流速加快。

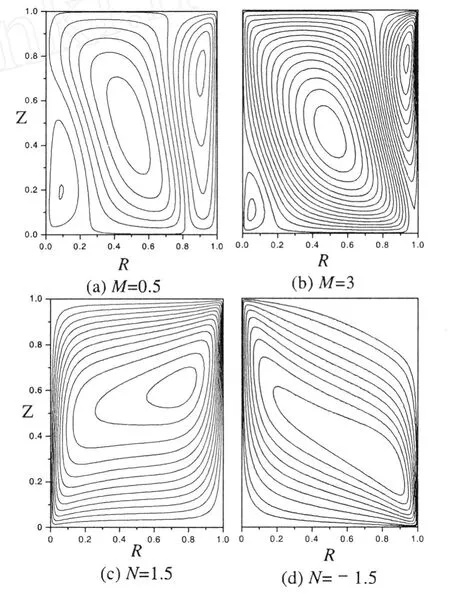
圖3 等流函數圖

由圖3(c)、(d)可知,N由 1.5變為-1.5后,二浮力作用由相互加強變為相互削弱。物質擴散浮力的影響逐漸占優并決定了流場內流體流動方向,使得流場內流型發生反轉,由順時針流動變為逆時針流動且流體流動加快流線再次變得較為密集。

3.3 Nusselt數和Sherwood數

為定量考察傳熱傳質過程受內熱源分布系數的影響,定義內壁面Nusselt數和上壁面Sherwood數為:

圖3給出了A=3,Le=2,N=-0.5時不同內熱源分布系數M下Nusselt數和Sherwood數的變化。圖4反應了內壁面Nusselt數的變化情況,可以看出在 Z＜0.7處 Nusselt數均變化平緩,Z＞0.7時Nusselt數均沿軸向減小,表明Z=0.7附近,壁面處流體溫差開始減小,對流傳熱隨之減弱。隨M增大,內壁面Nusselt數變化范圍增大,并且轉折點前移,表明隨著內熱源強度分布梯度增大,流體對流傳熱作用愈加明顯。

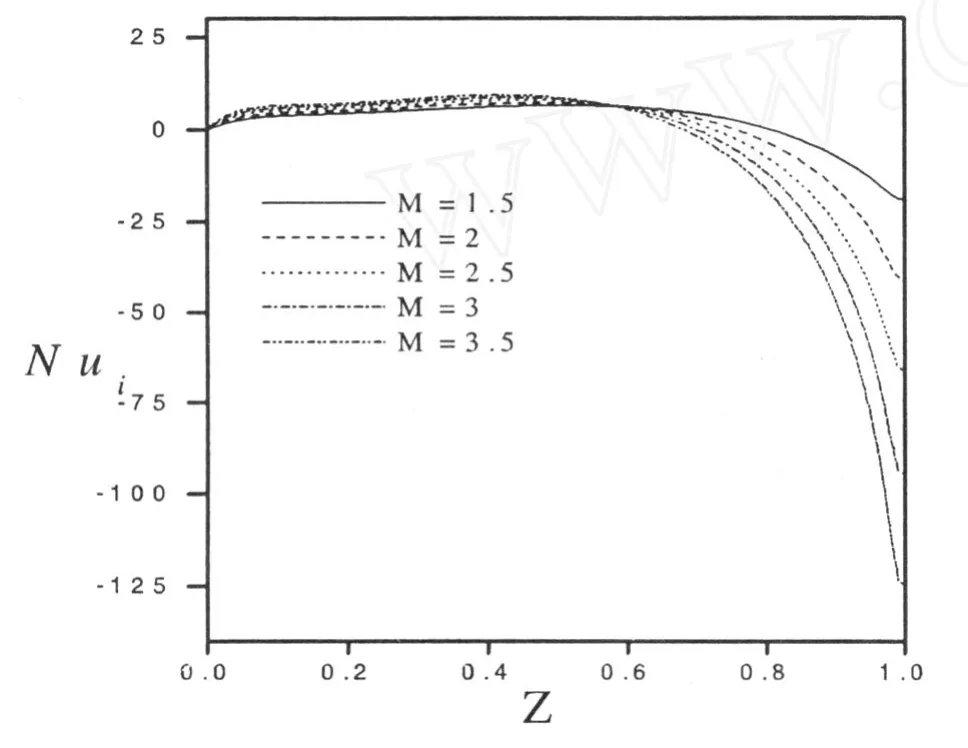
圖4 Nusselt數分布

圖5給出了上壁面局部Sherwood數沿徑向的變化。N=-0.5時,溫度和濃度產生相互加強的耦合作用,Sherwood數先增大后減小在R=0.9處出現轉折。隨M增大,Sherwood數增大,表明內熱源溫度梯度的增加,使傳質效果愈加明顯。

4 結論

(1)內熱源在徑向上分布系數M和浮力比N對流場、溫度場和濃度場影響顯著。在M較大時,套管中部流體溫度高于內、外壁面附近流體溫度,造成流場中心的逆時針環流向中心擠壓。同時,內熱源的加熱強度增大造成流速加快。

浮力比N由1.5變為-1.5后,二浮力作用相互削弱。物質擴散浮力的影響逐漸占優并決定了流場內流體流動方向,使得流場內流型發生反轉。

圖5 Sherwood數分布

(2)Nusselt數在Z=0.7處出現轉折,表明在Z=0.7附近,壁面處流體溫差開始減小,對流傳熱隨之減弱。隨M增大內壁面Nusselt數變化范圍增大,并且轉折點前移,表明隨著內熱源強度分布梯度增大,流體對流傳熱作用愈加明顯。上壁面 Sherwood數也呈先增大后減小的趨勢,并且在R=0.9處出項轉折。表明內熱源分布梯度增大有助于傳熱傳質。

[1]林瑞泰.多孔介質傳熱傳質引論 [M].北京:科學出版社,1995.

[2]K.C.Leong.Numerical modeling of combined heat and mass transfer in the adsorbent bed of a zeolite/water cooling system[J].Applied Thermal Engineering,2004,24(16):2359～2374.

[3]B V Rathish Kumar,Shalini.Free convection in a non-Darcian wavy porous enclosure[J].International Journal of Engineering Science,2003,41(16):1827～1848.

[4]Kladias N,Prasad V.Flow transitions in buoyancy-induced non-Darcy convection in a porous medium heated f rom below.Journal of Heat Transfer,Transactions ASME.1990,112(3):675～684.

[5]梁森森,施明恒.含內熱源可燃性多孔介質中的傳熱研究[J].能源利用與研究,2005,22(01):19～27.

[6]A.Deiber,Bortolozzi.A two-field model for natural convection in a porous annulus at high Rayleigh numbers.Chemical Engineering Science,1998,53(8):1505～1516.

Numerical Analysis of Heat and Mass Transfer in Porous Media With a Non-uniform Heat Source

Li Dong,Tu Zhengyu,Li Xianyu,Deng Yumei
(Tian Jin Bohai Vocational&Technical College,Tian Jin 300221 China)

A numerical analysis is conducted for combined heat and mass transfer by natural convection in the vertical annulusfilled with saturated porous medium with a non-uniform generation.With the buoyancy ratio N decrease f rom 1.5 to 1.5,the reverse circulations in the center of the velocity field expanded,as well outside Nusselt number and the Sherwood number increase with M.

porous media;mixed convection;heat transfer,numerical analysis