理想單子在非標(biāo)準(zhǔn)飽和模型下的若干應(yīng)用
王茜,陳東立,馬春暉
(1.西安建筑科技大學(xué)理學(xué)院,陜西西安 710055;2.空軍工程大學(xué)理學(xué)院,陜西西安 710051)
理想單子在非標(biāo)準(zhǔn)飽和模型下的若干應(yīng)用
王茜1,2,陳東立1,馬春暉1
(1.西安建筑科技大學(xué)理學(xué)院,陜西西安 710055;2.空軍工程大學(xué)理學(xué)院,陜西西安 710051)
通過(guò)利用非標(biāo)準(zhǔn)分析中的飽和模型,對(duì)其中的理想進(jìn)行了討論,從而得到了理想的非標(biāo)準(zhǔn)特征,并進(jìn)一步利用這一特征證明了單子論中的一些相關(guān)定理.
理想;理想單子;飽和模型
1 引言
非標(biāo)準(zhǔn)分析,是利用數(shù)理邏輯的方法來(lái)探討和刻畫(huà)微積分的理論基礎(chǔ),為數(shù)學(xué)開(kāi)辟了新的研究領(lǐng)域;是使用非標(biāo)準(zhǔn)模型研究各種數(shù)學(xué)問(wèn)題的新的數(shù)學(xué)理論.它利用現(xiàn)代數(shù)理邏輯的概念和方法證明了實(shí)數(shù)結(jié)構(gòu)R可以擴(kuò)張[1]為包含無(wú)窮小與無(wú)窮大數(shù)的超結(jié)構(gòu)?R[2],在嚴(yán)格的數(shù)學(xué)基礎(chǔ)上恢復(fù)了萊布尼茨的作為“更合于發(fā)明家的藝術(shù)”的無(wú)窮小方法.這個(gè)方法無(wú)論在刻畫(huà)概念,證明定理,思考問(wèn)題等方面都顯示出優(yōu)越性.用無(wú)窮小方法,可使許多概念的刻畫(huà)顯得直觀,簡(jiǎn)明,可使定理的論證縮短.它使萊布尼茨的無(wú)窮小問(wèn)題得到了圓滿的解決.在分析的標(biāo)準(zhǔn)模型中,或者說(shuō)在實(shí)數(shù)域上展開(kāi)的分析學(xué)稱為標(biāo)準(zhǔn)分析;把實(shí)數(shù)域及其上的關(guān)系的擴(kuò)大成為分析的非標(biāo)準(zhǔn)模型.本文所要討論的是用非標(biāo)準(zhǔn)分析的方法給出理想單子概念,并討論它在非標(biāo)準(zhǔn)飽和模型下的若干應(yīng)用,從而為理想單子的研究提供了一條新路徑.既推動(dòng)了非標(biāo)準(zhǔn)分析在不同應(yīng)用領(lǐng)域的發(fā)展,又給測(cè)度論賦有了更加內(nèi)在的探索意義.
2 預(yù)備知識(shí)
設(shè)X是無(wú)限集,X包含在非標(biāo)準(zhǔn)全域V(S)的個(gè)體集S中,V(?S)是S的非標(biāo)準(zhǔn)模型,于是有?X是X的擴(kuò)張,X??X[3].
定義1[4]設(shè)Γ?P(X),如果Γ滿足:
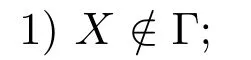
2)若A∈Γ,B?A,則B∈Γ;
3)若A∈Γ,B∈Γ,則A∪B∈Γ,
則稱Γ是X上的理想.
定義2設(shè)Γ是X上的理想,稱ν(Γ)=∪{?G:G∈Γ}為Γ的單子.
定義3若DA={I:I?X且A??I},則稱νd(A)為Γ的離散單子,其中νd(A)= ν(DA).
定義4[1]設(shè)r是V(?S)上的一個(gè)內(nèi)二元關(guān)系,A?dom(r),若對(duì)于任意的x1,x2,…,xn∈dom(r),均存在某個(gè)內(nèi)二元y∈V(?S),使得〈xi,y〉∈r,(i=1,2,…,n),則稱r是A中的一個(gè)共點(diǎn)關(guān)系.
定義5[5]設(shè)κ為無(wú)限基數(shù),若對(duì)V(?S)中的每個(gè)內(nèi)二元關(guān)系r,當(dāng)r滿足card(A)<κ 時(shí)(A?dom(r)),均存在內(nèi)元b∈V(?S),使得對(duì)于任意的a∈A,滿足〈a,b〉∈r,則稱V(?S) 為κ飽和的.
3 上下溢原理
上、下溢原理是非標(biāo)準(zhǔn)模型中一個(gè)常用的技巧性重要工具,在非標(biāo)準(zhǔn)分析的許多問(wèn)題中都會(huì)用到它,如著名的LOEB測(cè)度空間的構(gòu)造.本文在非標(biāo)準(zhǔn)的飽和模型中用理想單子來(lái)刻畫(huà)它.
定理1設(shè)X是無(wú)限集,?X是X的擴(kuò)張.則以下命題等價(jià):
(1)對(duì)X上的任意理想Γ,?X的所有內(nèi)子集A,若對(duì)任意的I∈Γ,?I∪A/=?X,則ν(Γ)∪A/=?X.
(2)對(duì)X上的任意的理想Γ,若Λ是?Γ的一個(gè)內(nèi)子集,Γ=?Λ,則存在E∈Λ使E?ν(Γ).
(3)對(duì)X上的任意理想Γ,若Λ是?Γ的一個(gè)內(nèi)子集,E∈?Γ且E?ν(Γ)有E∈Λ,則存在一個(gè)I∈Γ使得?I∈Λ.

定理1中條件(1)在非標(biāo)準(zhǔn)擴(kuò)大模型中未必成立,但在非標(biāo)準(zhǔn)飽和模型中結(jié)論顯然是成立的,從而在非標(biāo)準(zhǔn)飽和模型中結(jié)論(2)和(3)也成立.(2)和(3)則充分體現(xiàn)了上下溢原理的本質(zhì)內(nèi)涵.
下面利用定理1給出理想的離散單子在飽和模型中的一些應(yīng)用.
理想的離散單子是理想單子的特殊情形.首先DA是一個(gè)理想單子,而由其表達(dá)式DA= {I:I?X且A??I}及νd(A)=ν(DA)可知理想的離散單子就是理想單子的特殊情形.由于它的特殊性,我們就進(jìn)一步的給出其更具體的應(yīng)用.
定理2設(shè)X是無(wú)限集,?X是X的擴(kuò)張.?X為κ飽和,κ>card(X).

[1]陳東立,馬春暉,史艷維.擴(kuò)大模型的充要條件及其應(yīng)用[J].西安建筑科技大學(xué)學(xué)報(bào),2004,36(2):243-245.
[2]潘紅霞,陳東立,史艷維.飽和模型的充要條件及其應(yīng)用[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2006,22(1):131-133.
[3]陳東立,馬春暉,史艷維.拓?fù)涞姆菢?biāo)準(zhǔn)定[J].西北大學(xué)學(xué)報(bào):自然科學(xué)版,2006,36(3):348-350.
[4]史艷維,陳東立,馬春暉.理想收斂理論的非標(biāo)準(zhǔn)刻畫(huà)[J].西安建筑科技大學(xué)學(xué)報(bào),2005,37(2):294-296.
[5]Luxemburg W A J.A General Theory of M onads[M].New York:W iley,1969.
The idealm onad under the app lication of nonstandard model saturation
WANG Qian1,2,CHEN Dong-li1,MA Chun-hui1
(1.School of Science,Xi’an A rchitecture and Technology University,Xi’an 710055,China; 2.College of Science,A ir Force Engineering University,X i’an 710051,China)
In this paper,the ideal in exspend model using non-standardized expand model is discussed giving the non-standard characteristics of ideal.Furthermore,it is to prove some related theorems in monad.
ideal,idealmonad,saturation
O141.41
A
1008-5513(2009)02-0258-03
2007-11-05.
陜西省自然科學(xué)基金(2007A 12),西安建筑科技大學(xué)基礎(chǔ)研究基金(JC 0620),西安建筑科技大學(xué)青年科技基金(QN 0736).
王茜(1983-),碩士,研究方向:非標(biāo)準(zhǔn)分析.
2000M SC:03H 05

