仿生減搖鰭升力模型的數值模擬及分析
李冬松 金鴻章
1哈爾濱工程大學 自動化學院,黑龍江 哈爾濱150001
2哈爾濱工業大學 數學系,黑龍江 哈爾濱150001
仿生減搖鰭升力模型的數值模擬及分析
李冬松1,2金鴻章1
1哈爾濱工程大學 自動化學院,黑龍江 哈爾濱150001
2哈爾濱工業大學 數學系,黑龍江 哈爾濱150001
船舶在系泊或低航速狀態下,發動機主機停止工作,船舶失去自控方向能力,船體隨波浪左右搖晃,比航行時搖擺更為劇烈。因此,研究零航速減搖鰭非常重要。文章研究零航速時仿生減搖鰭產生升力的模型,其基礎為Weis-Fogh機構理論。首先討論如何旋轉才能產生給定的升力。依據呂卡提方程理論,給出模型周期解的存在性和穩定性條件;采用單步Runge-Kutta方法求出模型的數值解,給出保證數值解穩定的條件。
減搖鰭;零航速;呂卡提方程;周期解;穩定性;仿生學
1 引言
常規減搖鰭是目前最常用且應用最成功的船舶主動式減搖裝置,減搖效果可達90%以上。然而,只有船舶的航速較高時,減搖鰭才可以有效地減搖,船舶在低航速或零航速情況下,減搖鰭幾乎不能進行減搖。這是由其減搖機理決定的,即減搖鰭升力的產生需要高速水流流過鰭表面。當速度很小時,鰭上的升力也變得很小,在零航速時升力也同時消失了。對于在低航速或系泊狀態下仍需要減搖的船舶來說,傳統的減搖鰭就不再適用了。而減搖水艙減搖效果有限,有時甚至出現增搖現象,這就要求發展零航速減搖鰭技術,此技術在減搖領域一直是個空白。本文依據Weis-Fogh機構理論設計零航速減搖鰭。Weis-Fogh機構是英國的生物學家發明的一種仿生機構,這種機構能在無來流速度的流體中產生升力,這一特性在零航速減搖鰭中得到了應用[1-7]。圖1為Weis-Fogh機構的簡化模型,它由兩個平板翼組成,當Weis-Fogh機構張開時,兩個平板翼的翼根點緊緊靠在一起,前緣點B分開,兩翼繞A點轉動張開,張開角為2απ,角速度為Ω,兩翼間形成空隙,迫使周圍流體充填該空隙。由于流體不可壓縮,當張開角很小時,流體充填空隙的速度非常高,造成兩翼上下表面很大的壓力差。當Weis-Fogh機構閉合時,兩翼對空隙間的流體產生壓力,迫使流體流出空隙。與張開時類似,當張開角很小時,流體流出空隙的速度非常高,造成兩翼上下表面很大的壓力差。當Weis-Fogh機構張開或閉合時,機構運動是對稱的,這種對稱性可以在一定程度上簡化理論分析。
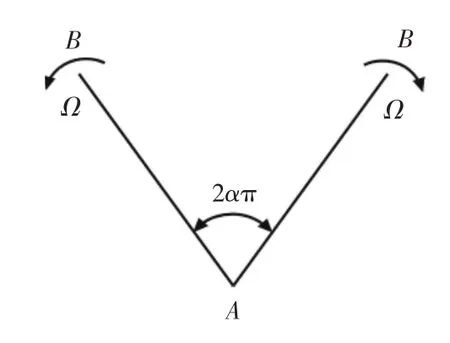
圖1 Weis-Fogh機構物理模型
采用Weis-Fogh機構來設計零航速減搖鰭,首先要對它的升力特性進行分析。由于Weis-Fogh機構的對稱性,只需對單翼進行升力分析,由對稱性即可得到兩翼共同作用的升力特性。由伯努利方程求出物面壓強p的表達式,將壓強沿物面積分,經復雜的推導得出流體對翼的作用力。由文獻[8]得,作用于機翼上的力可以表示為角加速度和來流加速度的一次函數的線性組合;角速度和來流速度的二次函數的線性組合,即升力:
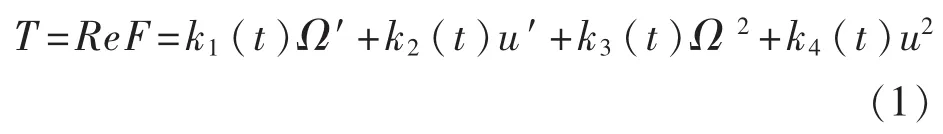
式中,u為來流速度;u′為來流加速度;Ω為翼的旋轉角速度;Ω′為翼的旋轉角加速度。
當討論零航速時,來流速度u=0,來流加速度u′=0。如令T=f1(t),Ω=y(t),Ω′=y′(t),從而式(1)可以簡化成:
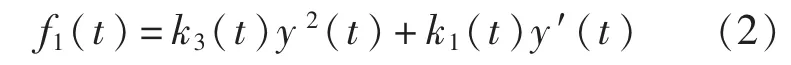
本文研究翼如何旋轉才能產生船舶減搖所需要的指定升力f1(t),此時問題轉化為求解下面微分方程:

由文獻[7],m1<a(t)<M1<0。本文僅考慮升力控制,由于翼回擺時產生的反向力涉及到翼的變形,我們將再另文研究。在此簡化條件下,模型中a(t)成為周期函數,周期為2π。
2 模型數值解的分析及在減搖鰭控制中的應用
首先介紹模型精確解的性質,當所需升力f(t)是周期為2π的連續函數時,模型為呂卡提方程,呂卡提方程近年來得到廣泛的研究[9-10]。
模型的示性代數方程為

由文獻[8],a(t)<0,升力f(t)>0,故a(t)f(t)<0。當a(t),f(t)為周期為2π的連續函數時,依據呂卡提方程性質,已知方程(3)存在兩個周期為2π的連續解y1(t),y2(t),且y=y1(t)為穩定的周期解,y=y2(t)為不穩定的周期解。
由于常微分方程的精確解難以求出,故需要采用數值方法求方程的近似解,本文采用單步Runge-Kutta方法,它具有精度高,穩定性好的特點。對升力模型:
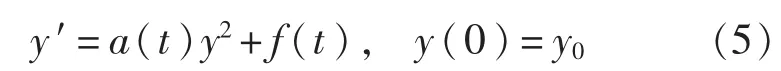
采用Runge-Kutta方法離散得:
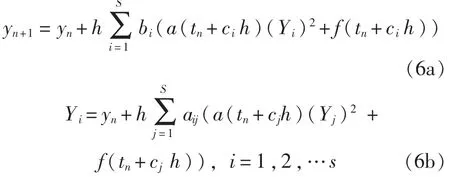
式中,f∈C∞,f(t+2π)=f(t),y0是已知數,A= aij)s×s,b=(b1, …,bs),c=(c1, …,cs) 由具體Runge-Kutta方法確定。
下面首先進行幾個數值試驗,探討離散模型的性質。
試驗1 y=-2y2+(2-sin(t)),y(0)=5。
使用Heun’s公式得:圖2。

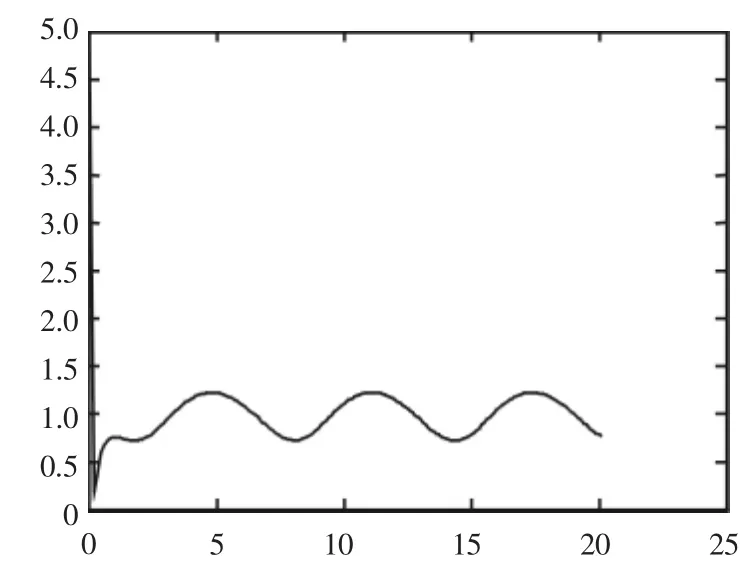
圖2 試驗1中數值解在t=5時呈現周期性
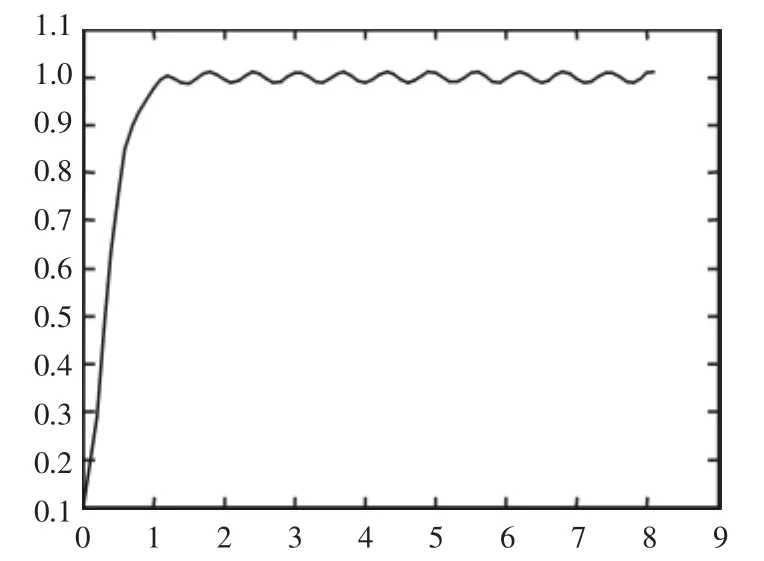
圖3 試驗2中數值解在t=2時呈現周期性
試驗2 y′=-2y2+(2-sin t),y(0)=0.1。仍使用Heun’s公式,計算結果見圖3。
試驗3 y′=-10y2+(2-cos(2t)),y(0)=0.1,h=0.1。
當方程為y′=f(t,y)時,Euler公式為yn+1=yn+f(tn,yn),應用于模型得:

計算結果如圖4。
試驗4 y=-10y2+2-cos(2t),y(0)=1,仍使用Euler公式,結果如圖5。
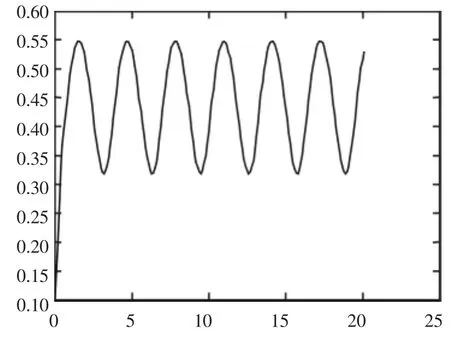
圖4 試驗3中數值解在t=1時呈現周期性
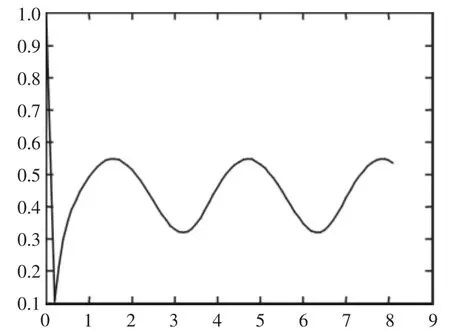
圖5 試驗4中數值解在t=0.4時呈現周期性
從數值試驗中可觀察出以下結論,當步長較小時,數值解保持精確解的漸近周期性。但在研究方程y′=-10y2+2-cos(2t)時,我們發現,當初值y(0)較大,如y(0)=2,h=0.1,數值解不穩定,發散速度極快。這說明離散控制時,還應考慮步長h,下面討論步長的選取問題。
3 離散模型的穩定性分析
下面研究Runge-Kutta方法求解方程 (5)的漸近周期性,將R-K法應用于方程(5)可得離散模型:
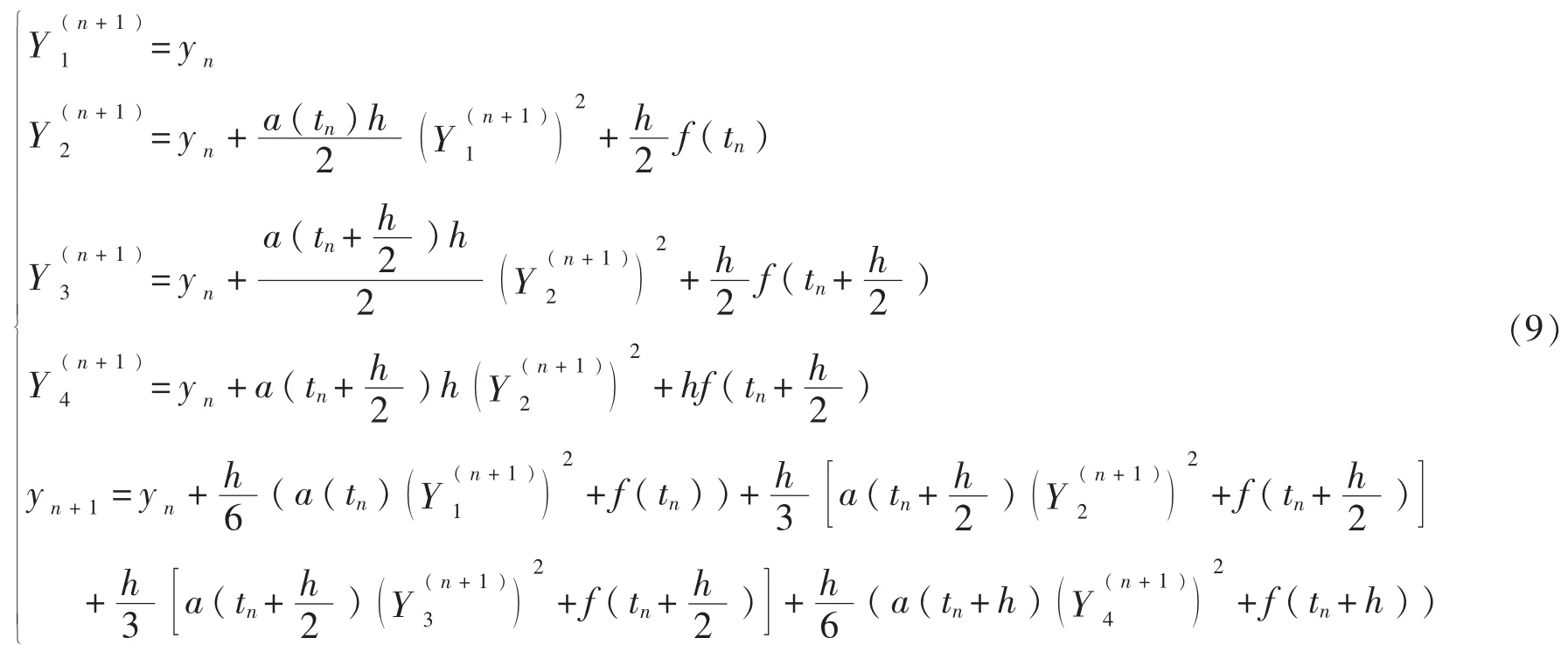
此處,h=2π/N,N是正整數。
引理1 設a(t)<0,f(t)>0,a(t),f(t)∈C,且a(t)=a(t+2π),f(t)=f(t+2π),t>0,令K=max}和h0如果0<h<h0,則存在正數M,m和N,使得m<yn<M,m<Y<M,i=1,2,3,4,n>N。
證明:設初始值y0>mF+MF,則(Y)2+ h 2 f(t0)<0,由式(9)得,Y<y0。 因為h<h0<,我們有
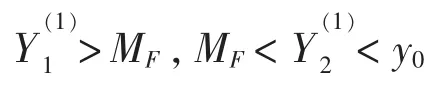
同樣道理,
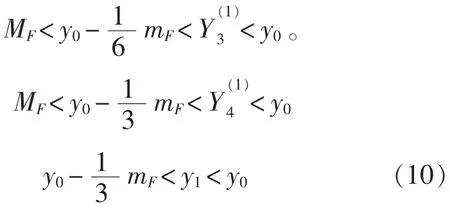
設y0>y1>…>yN-1>yN,yN 式(12)與yN-1>yN矛盾。使用歸納法即可得,若干步后數值解將在mf和K之間振動。定理證畢。 用類似的方法還可證明 定理1 設a(t)<0,f(t)>0,a(t),f(t)∈C,a(t)=a(t+2π),f(t)=f(t+2π),t>0, 由以上研究可得在計算升力時,必須注意步長的選取,否則將失去穩定性。 船舶零航速仿生減搖鰭仍處于研究階段,有大量的理論和實際問題需要解決。本文討論Weis-Fogh機構如何旋轉才能產生船舶減搖所需要的指定升力及穩定性問題,首先論證了升力模型穩定性,然后給出保證數值解穩定的步長選取條件,為仿生減搖鰭的控制打下理論基礎。實際上關于Weis-Fogh機構的理論還有很多工作要做,如可變翼的升力模型的計算,及回擺時力的計算,這些工作將在以后研究。 [1]王宇,金鴻章.船舶零航速減搖鰭升力測量研究[J].傳感器與微系統,2007,26(1):11-14. [2]JIN HZ,WANG Y,QI Z G.Study on lift generation of Weis-Fogh flapped fin stabilizer at zero speed[C]//Korea,Busan:SICE-ICASE International Joint Conference,2006. [3]JIN H Z,QI Z G,WANG Y.Research on ship roll stabilization at zero speed[C]//Korea,Busan:SICEICASE International Joint Conference,2006. [4]DANIEL T,COMBES S A.Flexible wings and fins:bending by inertial or fluid dynamic forces[J].Integrative Comparative Biology,2002,42(5):1044-1049. [5]SANE S P,DICKINSON M H.The aerodynamic effect s of wing rotation and a revised quasi2steady model of flapping flight[J].Journal of Experimental Biology,2002,205:1087-1096. [6]王宇,金鴻章,綦志剛,等.船舶零航速減Weis-Fogh減搖鰭升力仿真研究 [J].海軍工程大學學報,2007,19(3):21-25 [7]SOHN M H,CHANG J W.Flow visualization and aerodynamic load calculation of three types of clap-fling motions in a weis-fogh mechanism [J].Aerospace Science and Technology,2007,11(2-3):119-129. [8]章社生,王獻孚,吳秀恒.Weis-Fogh機構流體力學[M].北京:國防工業出版社,1999. [9] BALASUBRAMANIAM P,SAMATH J A,KUMARESAN N,et al.Solution of matrix Riccati differential equation for the linear quadratic,singular system using neural networks[J].Applied Mathematics and Compution,2006,182(2)1832-1839. [10]ZHU J,LI K.An iterative method for solving stochastic Riccati differential equations for the stochastic LQR problem[J].Optimization Methods and Software,2003,18(6),721-732. The Analysis and Numerical Simulation for the Lift Model of Fin Stabilizer Li Dong-song1,2Jin Hong-zhang1 The engine of ships is laid off at anchor.Ships drift with wave and loss the capacity of controlling navigating direction for self,so the roll is increased and severer than shipping state.It is important to study stabilizer when a ship is at zero speed.In this paper we study the lift model of fin stabilizer that based on potential theory of the Weis-Fogh mechanism when a ship is at zero speed.Firstly,we discussed that Weis-Fogh mechanism how to rotate to generate the lift that has been given.According to the theory of Riccati differential equation,conditions that assure the existence and stability of period solution are given.Then,using Runge-Kutta methods,the numerical solution of the model is obtained.Finally we give the conditions that assure the numerical solution is stable.The results are closely matched with numerical experiments. antirolling fin;zero speed;Riccati differential equation;periodic solution;stability;bionics TP212 :A :1673-3185(2009)01-29-04 2008-10-1 2 國家自然科學基金(50575048);黑龍江省博士后資助項目(LBH-205052) 李冬松(1963-),男,副教授,博士。研究方向:延遲微分方程精確解和數值解的定性性質。 E-mail:lds_ch@yahoo.com.cn 金鴻章(1946-),男,教授,博士生導師。研究方向:控制理論和控制系統、智能控制、船舶控制系統與減搖裝置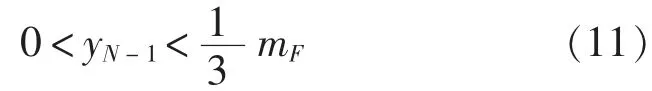

4結論
1 College of Automation,Harbin Engineering Univ.,Harbin 150001,China 2 Dept.of Mathematics,Harbin Institute of Technology,Harbin 150001,China

