聚氨酯隔振器試驗建模與參數辨識

1 引 言

利用非線性彈性和阻尼元件控制振動日益受到重視。與線性元件相比，非線性元件具有衰減大沖擊和吸收寬頻帶振動的特征，所以更為有效。聚氨酯隔振器是一種承載范圍寬的新型非線性隔振器。本文通過大量試驗,對聚氨酯隔振器動態特性進行了研究。試驗研究表明，聚氨酯隔振器的遲滯特性不僅與振幅有關，還與頻率有關；恢復力同時受頻率和振幅的影響，具有非線性滯后特性。在此基礎上結合理論分析,建立了隔振器模型,該模型將恢復力分解為非線性彈性力和非線性阻尼力兩部分。對比理論與試驗結果表明,所建模型可靠,能夠合理描述隔振器的非線性遲滯特性,為其隔振動態特性研究奠定了重要的理論基礎。

2 聚氨酯隔振器動態特性試驗

2.1 試驗元件及測試設備

由于傳統的激振方法(例如錘擊、激振器和振動臺)難以滿足大振幅、頻率和激振力變化范圍的要求。為了更加方便地激發出高次非線性,提高參數識別精度,運用美國MTS公司810型液壓伺服試驗系統，該系統采用微機數控和電液伺服，配置的位移、載荷、應變3種傳感器都很精確，精度為0.5%，有良好的頻率控制和幅值控制特性，同時能由微機自動記錄所有數據，是測試隔振器靜態和動態性能的理想設備，完全滿足測試要求。

試驗裝置及隔振器安裝示意圖如圖1所示。

圖1 試驗元件在MTS材料試驗機上安裝圖

2.2 試驗及結果分析

在MTS材料試驗機上采用位移控制方式的正弦位移加載試驗,將從試驗機自帶的力、位移傳感器反饋回來的信號進行濾波去噪，編制MATLAB程序，可得到許多相應的曲線圖，如圖2和圖3所示。圖2表示激振頻率為4 Hz，振動幅值為±0.5 mm、 ±1.0 mm、±2.0 mm的恢復力—位移圖。圖3表示振動幅值為2 mm，激振頻率分別為2 Hz, 6 Hz,10 Hz的位移恢復力圖。

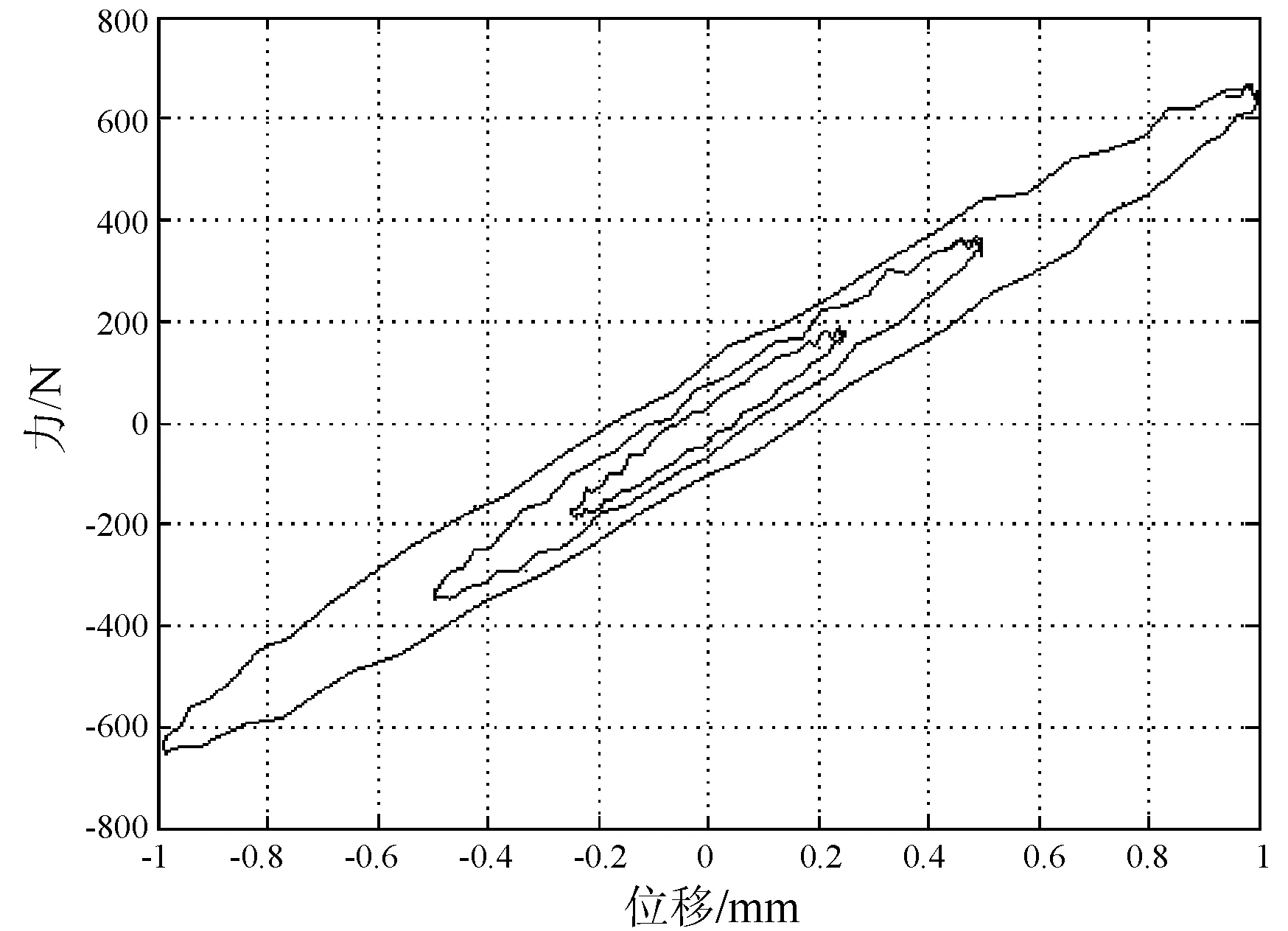
圖2 遲滯回線隨振幅變化的圖形(頻率4 Hz)

圖3 遲滯回線隨頻率變化的圖形(振幅2 mm)

由圖2遲滯回線隨振幅的變化可知:

1) 振幅不同,即使位移相同,恢復力也不同,即恢復力與變形歷史有關;

2) 振幅不同,隔振器的平均剛度也略有不同；

3) 恢復力具有明顯的滯后特性,遲滯回線的面積(表示隔振器所耗散的能量)隨振幅發生改變,說明隔振器的阻尼與振幅有關,隔振器的動剛度和阻尼均是振幅的非線性函數;

4) 遲滯回線的形狀接近橢圓,隨著振幅的增大,遲滯回線的形狀發生改變,說明恢復力中的阻尼成份并不單一。

由圖3遲滯回線隨頻率的變化可知:

1) 頻率不同,隔振器的平均剛度隨之改變;

2) 遲滯回線的面積隨著頻率的改變而變化,說明隔振器的阻尼與頻率有關。

綜上所述,聚氨酯隔振器的恢復力同時受振幅和頻率的影響,與變形歷史有關, 其本構關系是一個復雜的非線性泛函。

3 隔振器動力學模型及參數識別

迄今為止,最具代表性的非線性遲滯系統數學模型主要有以下幾種:雙線性恢復力模型[1];Bouc-Wen模型[2,3]、跡法模型[4]。這些模型各有不同的應用場合和優缺點。

雙線性恢復力模型優點是結構形式簡單,各參數物理意義明確,需要辨識的參數少,缺點是將系統處理成兩個線性剛度系數,無法描述強非線性高階剛度系數的影響,將阻尼僅處理成干摩擦阻尼,不足以描述復雜阻尼情況; Bouc-Wen模型優點是可以描述大小不同、形狀各異的遲滯回線,缺點是恢復力表達式中彈性力和阻尼力不明確,各參數物理意義不清晰,參數中出現了一階微分方程不利于參數識別,這種模型多用于滯后系統的隨機振動響應分析; KO[5]等提出的基于平均和等效原理的跡法模型優點是各個參數的物理意義明確,表達式簡單,但是由于實際結構很復雜,可能同時存在多種阻尼,因此阻尼僅描述為等效的粘性阻尼往往反映不了實際情況。潘東[6]等在跡法模型的基礎上提出了一種混合阻尼模型來描繪鋼絲繩遲滯特性，結果表明該模型能夠合理反映兼有不同性質阻尼的滯后非線性特性。

3.1 非線性彈性復合阻尼模型

分析由動態試驗得到的圖4可知，遲滯回線可以分成上下2條,分別對應速度大于零及小于零的情況。大多數情況下可以認為上下半支遲滯回線是關于位移反對稱的。用冪函數多項式分別擬合上下半支遲滯回線,假設用于擬合上半支遲滯回線的冪函數多項式為:

(1)

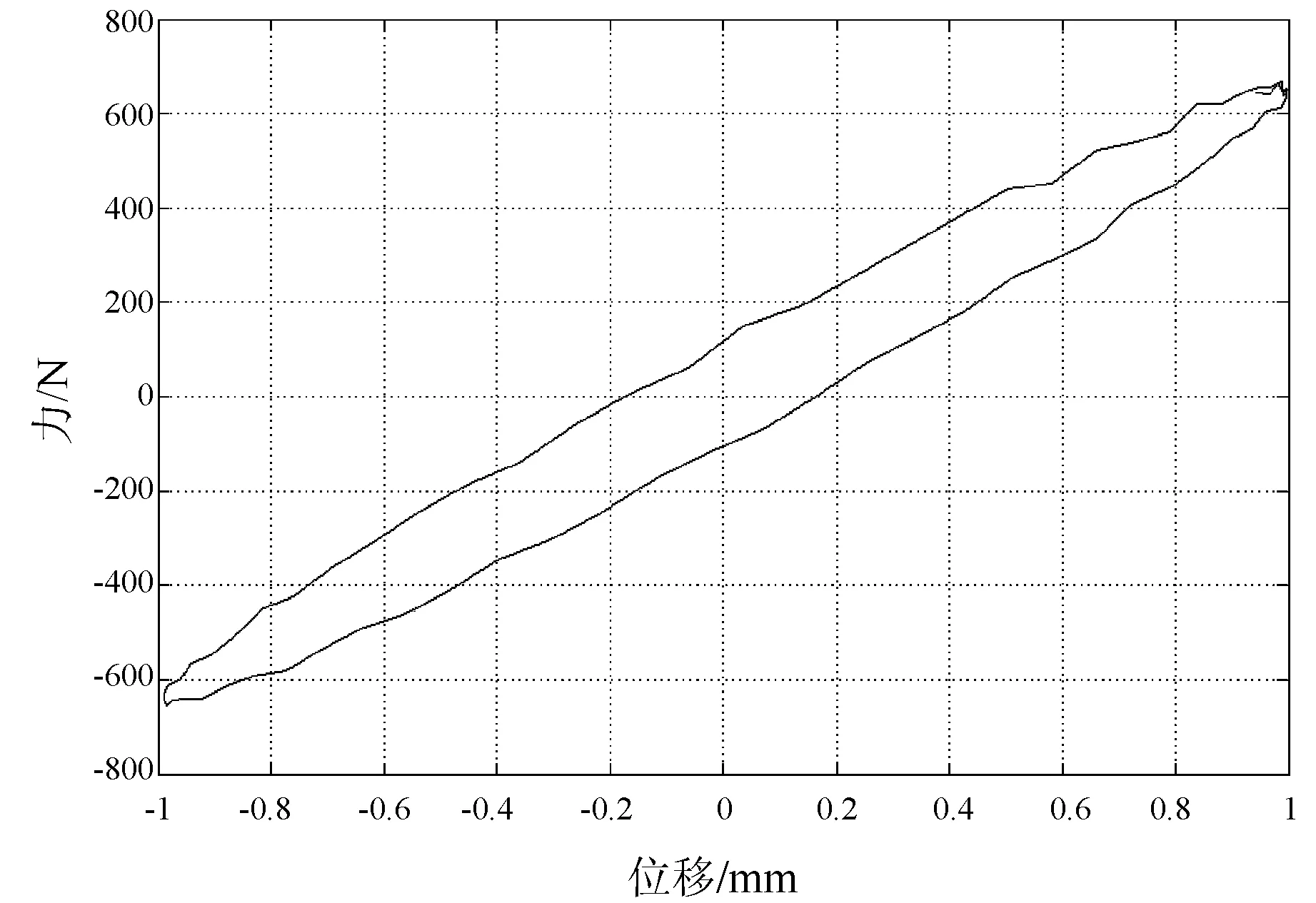
圖4 聚氨酯隔振器動態特性圖(預壓5 mm,振幅2 mm)

由位移反對稱原理FX(x)=-FS(-x)，則用于擬合下半支遲滯回線的多項式為:

(2)

上式中，FS(x)、FX(x)分別表示遲滯回線的上下分支。其中x為隔振器變形,ai表示冪函數多項式的系數。冪函數多項式項數n,按擬合的遲滯回線形狀和對表達式要求的精度而定。

將式(1)、式(2)的冪函數多項式按奇、偶項分開寫為:

(3)

(4)

兩式合并為:

(5)

遲滯恢復力中彈性恢復力Fk(x)為弱非線性,因此取前兩階展開式即可。構造非線性彈性恢復力Fk(x)的數學模型為:

Fk(x)=k1x+k3x3

(6)

圖5 遲滯回線擬合分解圖

由于產生阻尼的因素較多,恢復力中存在多種阻尼成份,若僅用一種阻尼描述,則與實際情況相差較遠。因此,在模型中引入反映阻尼組成的阻尼成份因子,構造非線性阻尼力數學模型為:

(7)

式中,c為阻尼系數,α為阻尼成份因子。由上式可以看出:α越大,阻尼力對速度的變化越敏感;反之阻尼力對速度的變化就比較遲鈍。當α=1時,上式實際上就簡化為線性粘性阻尼;當α=0時,阻尼力僅與速度符號有關,上式表示的是干摩擦阻尼;當α在(0,1)范圍內變化時,表示的是既有干摩擦阻尼特性，又有粘性阻尼特性的混合型阻尼。由此可以看出,阻尼成份因子α可以很好地描述多種阻尼成份,且物理意義明確。

綜上所述,描述聚氨酯隔振器動態特性的非線性彈性復合阻尼模型為:

(8)

3.2 參數分解識別算法

針對該模型可采用非線性最小二乘最優化方法進行參數識別。基于最優化方法的參數識別，就是通過不斷調整參數向量使殘差和最小，即

(9)

式中，r(y)為殘差，y為待識別參數向量。解非線性最小二乘問題的牛頓迭代公式為[7]：

yk+1=yk-(J(yk)TJ(yk)+S(yk))-1J(yk)r(yk)

(10)

然而，在用MATLAB程序中的非線性最小二乘函數進行參數識別時發現，不僅計算周期長，而且計算過程中會出現矩陣病態，導致識別效果不甚理想。分析問題的產生可能存在以下原因：S(y)含二階算子，計算的工作量很大，甚至是難以計算；矩陣逆運算非常容易出現奇異，導致計算不能繼續進行。為了盡量避免非線性最小二乘法計算矩陣病態問題的出現，可采取的方法是盡量減少最優化識別時的參數數量。為此，本文采取參數分解識別方法。

1) 用動態試驗測量到的隔振元件位移、恢復力采樣信號xk,fk(k=1,2,3,…,n)對遲滯回線進行最小二乘多項式擬合,得到的多項式中奇數項系數即為待識別的非線性彈性恢復力剛度系數k1,k3。

2) 用已識別出的k1,k3及測量得到的位移采樣信號xk, 重構非線性彈性恢復力Fk(xk)。

Fk(xk)=k1x(t)+k3x3(t)

(11)

(12)

根據非線性阻尼力模型式(7),用Gauss-Newton非線性最小二乘參數識別算法[7],編制MATLAB程序, 即可識別出阻尼系數c及阻尼成份因子α。

3.3 參數識別算例

為驗證所建模型的可靠性與參數識別算法的準確性,我們利用隔振器動態試驗中測量的振幅2 mm,頻率4 Hz的位移及恢復力數據,對隔振器模型進行了參數識別,結果如表1所示,并用識別出來的參數進行了模型重構。模型重構結果與試驗曲線的比較見圖6,可以看出,兩者擬合得較好,說明所建模型可靠。

表1 模型參數識別結果(振幅2 mm,頻率4 Hz)

4 結 論

1) 通過隔振器動態試驗可知,聚氨酯隔振器的恢復力同時受激勵頻率和振幅的影響,并且和變形歷史有關,具有明顯的非線性遲滯特性，且隔振器中存在多種阻尼成份。

2) 通過試驗及理論分析建立了隔振器的動態數學模型,通過引入阻尼成份因子,使得該模型能較好地擬合隔振器中存在的各種復雜的阻尼成份。

3) 通過對比試驗曲線與仿真結果,驗證了數學模型和參數識別的準確性,下一步可利用該隔振器恢復力模型研究其隔振動態特性。

圖6 模型重構結果與試驗曲線對比(振幅2 mm,頻率4 Hz)

參考文獻:

[1] MASRI S F. Forced vibration of the damped bilinear hysteretic oscillator[J]. The Journal of the Acoustical Society of America, 1975,57(1): 106-112.

[2] BOUC R. Forced vibration of the mechanical systems with hysteresis[C]∥Proceedings of the fourth conference on nonlinear oscillation, Prague, Czechoslovakia, 1976：315-315.

[3] WEN Y K. Method for random vibration of hysteretic system[J]. Journal of the Engineering Mechanics Division, 1976,102(2):249-263.

[4] BADRAKHAN F. Rational study of hysteretic systems under stationary random excitation[J]. Int J Nonlinear Mechanics, 1987,22(4): 315-325.

[5] KO J K, NI Y Q, TIAN Q L. Hysteretic behavior and empirical modeling of a wire-cable vibration isolator[J]. Int J Anal Exp Modal Anal, 1992, 7(2):111-127.

[6] 潘東.滯后非線性彈性元件的試驗建模與參數辨識[D].上海:上海交通大學,1995.

[7] 袁亞湘,孫文瑜.最優化理論與方法[M].北京:科學出版社, 2001.