老師的神猜

周奕生

在一次課外活動中，老師對同學們說：“請同學們拿出一張月歷，隨便是哪年哪月的，然后用鉛筆按我的要求圈幾個數，只要告訴我這幾個數的和，我就能馬上猜出你們所圈的數．”

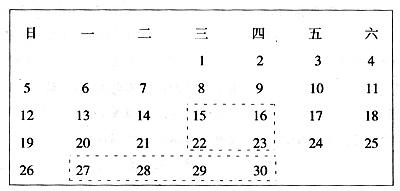
老師：請大家圈出同行連續四個數，然后告訴我這四個數的和，我馬上就能知道你們圈的四個數．

小明不信老師有那么大的本事．他拿出的月歷是２００４年９月份的，圈出２７至３０這四個數，然后大聲地說：“老師，我圈的四個數的和是１１４．”

老師：你圈的四個數是２７，２８，２９，３０．

小明：是的，您怎么這樣快就知道了？

老師：這是一種“魔術”，等一下再告訴你們吧．下面再請大家任意圈出同列相鄰的三個數，告訴我這三個數的和，我同樣知道你們圈的三個數．

又是小明一馬當先，他圈的是星期四這一列的最后三個數：“老師，我這一次圈的三個數的和是６９．”

老師：你圈的三個數是１６，２３，３０．

接著老師又說：大家用矩形任意圈出相鄰兩行和兩列的四個數，只需告訴我這四個數的和，我同樣知道你們圈的四個數．

這次是小慧眼明手快，圈出的四個數是星期三和星期四這兩列中的１５，１６，２２，２３，告訴老師這四個數的和后，老師稍加思索，就說出了答案．同學們驚得目瞪口呆．

請想一想，你能揭開老師神猜的秘密嗎？

其實這并不是什么魔術，而是老師掌握了月歷中數的排列規律．月歷中同行中的數都是連續正整數，后一個數總比前一個數大１；同列下一行的數總比上一行的數大７．你們只要記住這兩點，然后再列一元一次方程，什么問題都迎刃而解．

在第一個問題中，設第一個數是ｘ，則接下來三個數分別是ｘ＋１，ｘ＋２，ｘ＋３．已知這四個數的和是１１４，就得到了方程ｘ＋（ｘ＋１）＋（ｘ＋２）＋（ｘ＋３）＝１１４，即４ｘ＋６＝１１４． 解之得ｘ＝２７．

你看，這四個數不就知道了嗎？

原來這么簡單！第二個問題與第一個問題很相似．同學們揭開了第二個問題的秘密：設第一個數是ｘ，下一個數是ｘ＋７，再下一個數是（ｘ＋７）＋７＝ｘ＋１４，這三個數的和為６９，所以ｘ＋（ｘ＋７）＋（ｘ＋１４）＝６９，即３ｘ＋２１＝６９，解得ｘ＝１６，故三個數分別是１６，２３，２７．

老師：請你們自己想一想，第三個問題該怎么做呢？

事實上，月歷中還有許多規律，只要我們細心去觀察，留意去思考就能夠發現．比如我們可以圈出３×３，４×４這樣的方陣，還可以圈出菱形陣或三角形陣等等．不論什么問題，同行或同列相鄰兩數的關系是月歷中數的最基本特征，抓住這兩個特征，什么問題都可以解決．最后請大家探索一下：月歷中是否存在著如圖所示的菱形陣，使得７個數的和等于１４０或１０５？若存在，請求出這７個數；若不存在，請說明理由．