型鋼轉換集中荷載為線荷載情況分析

摘" 要：在既有房屋樓板安裝超重設備時通常需用型鋼對樓板進行加固或改變設備荷載分布形式，以滿足樓板承載力和安全要求。該文重點研究超重設備通過型鋼改變荷載形式時，型鋼傳遞荷載的長度及對樓板的影響。

關鍵詞：型鋼;荷載形式轉換;傳遞長度；樓板影響；線荷載

中圖分類號：TU312""""" 文獻標志碼：A""""""""" 文章編號：2095-2945（2025）04-0109-05

Abstract： When installing overweight equipment on the floor of an existing house， it is usually necessary to strengthen the floor or change the equipment load distribution form to meet the floor bearing capacity and safety requirements. This paper focuses on the study of the length of load transferred by the section steel and its impact on the floor when overweight equipment changes the load form through section steel.

Keywords： section steel; load form conversion; transfer length; floor influence; line load

筆者在設計院工作時曾從事電信機房承載力復核驗算及加固設計。其間常出現一個機房總荷載滿足要求，而電信設備因占地面積小又超重，形成集中荷載，遠遠超出樓板局部承載力。此時需采用型鋼將設備荷載傳遞至樓板周圍框架梁（圈梁）或將其分散傳遞至周邊的樓板共同承擔。對傳遞至周圍框架梁（圈梁）無需過多分析，本文重點對荷載分散至周圍樓板的加固形式進行分析。為進一步了解荷載通過型鋼對樓板的影響范圍，需研究荷載在型鋼上的傳遞長度，進而復核荷載對樓板的影響。

1" 型鋼傳遞荷載情況

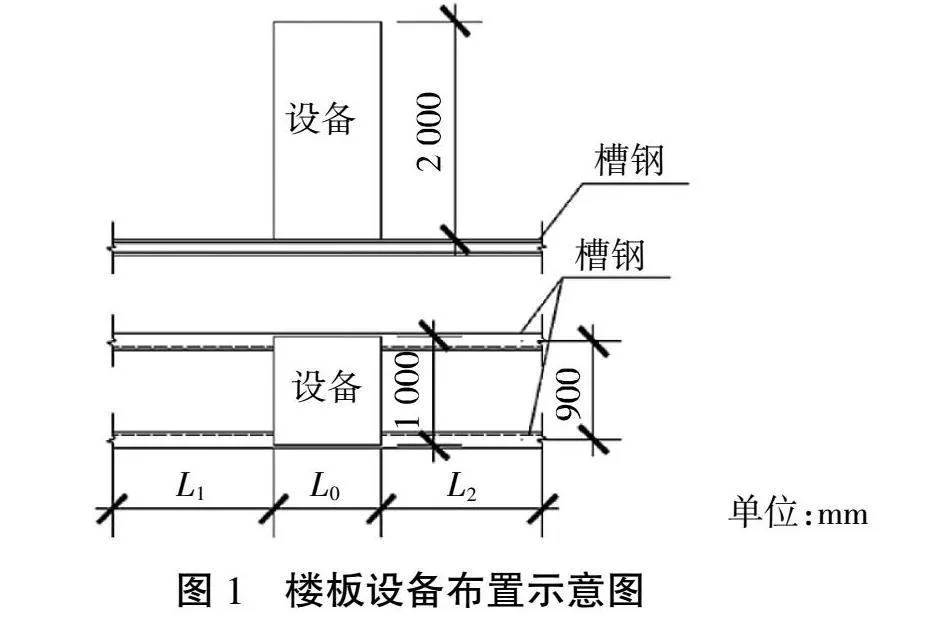
一般電信機房主要設備包含大容量蓄電池、傳輸設備、數據設備和交換設備等。設備通常是用螺栓固定在槽鋼上，再將槽鋼放置在混凝土樓板上。通過槽鋼將設備集中荷載轉換成兩線荷載，同時增加樓板承擔的范圍，提高了樓板的安全性。設備在沿型鋼長度分布時，根據實際空間情況，一對型鋼可以布置單臺設備，也可以布置多臺設備。為方便研究和簡化計算，我們從槽鋼布置單臺設備情況入手研究，如圖1所示。從圖1可以看出沿槽鋼長度方向可分割成數段，分別是設備放置段L0，設備左向槽鋼伸出段L1，設備右向槽鋼伸出段L2。對于多臺設備布置情況，設備左向槽鋼伸出段從最左向設備邊緣算起，設備右向槽鋼伸出段從最右向設備邊緣算起，設備之間空隙或間距忽略不計，均看作設備放置段。

設兩槽鋼上布置的設備總重為G，則單根槽鋼所受的設備荷載為P=G。沿槽鋼布置多臺設備時，設備放置段若占槽鋼總長70%及以下或是設備兩向槽鋼伸出段大于或等于1.5 m時，設備荷載按集中荷載簡化。本次研究主要是分析集中荷載放置在槽鋼情況，再延展到設備放置段占槽鋼總長70%以上或設備兩向槽鋼伸出段小于1.5 m情況。

根據力平衡條件，槽鋼在受到設備荷載同時也受到樓板的反力。樓板反力情況比較復雜，本文就是通過分析反力特征，建立計算模型，進而分析荷載在槽鋼的傳遞長度。

2" 型鋼受力分析計算的模型

2.1" 建立計算模型前的幾點假設

假設1：鋼材彈性模量大約是混凝土彈性模量的8倍，兩者剛度相差較大，在相同荷載作用下，兩者形變無法同步。但為能簡化計算，同時能滿足研究需求，從保守考慮，將鋼材剛度往低假設，對本次研究是有利的。再者，混凝土結構設計時為滿足正常使用功能，通常樓板受荷允許變形是微小的[1]；因此假設型鋼受荷變形與樓板混凝土形變滿足變形協調條件，即樓板形變產生的撓度與型鋼形變產生的撓度一致。

假設2：由于型鋼上通常放置多臺設備或單臺設備，設備放置段L0沿槽鋼長度方向有一定長度，設備和槽鋼經螺栓固定，形變時，型鋼與設備之間不產生左右滑移，因此假設槽鋼與設備為固接。

2.2" 型鋼計算簡圖選擇

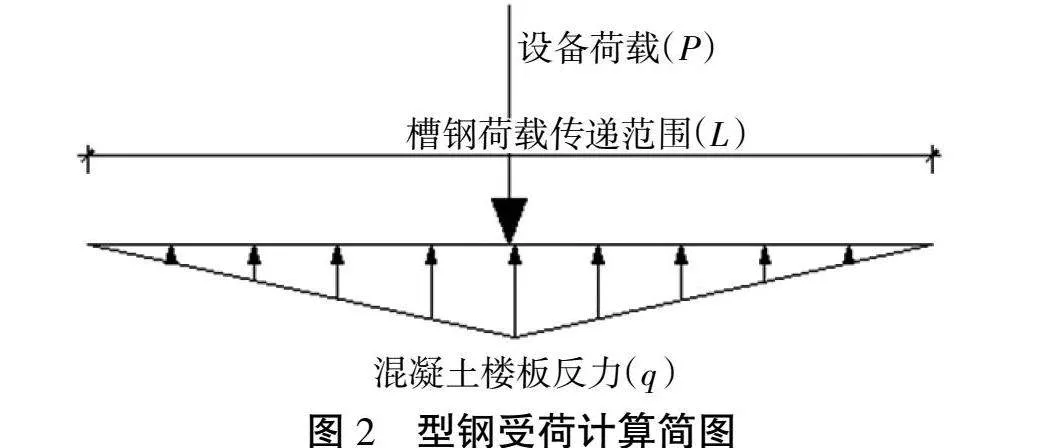
型鋼承受荷載并將其傳遞至混凝土樓板，其傳遞長度與型鋼剛度有很強的相關性。同時混凝土樓板受力產生撓度與混凝土樓板跨度是3次方或4次方關系，非線性。根據假設1：型鋼與混凝土樓板形變協調，型鋼變形也非線性，型鋼受到樓板反力有2種情況，當型鋼剛度較大，且型鋼長度超出設備較短時，可近似認為槽鋼剛度為無窮大。這時型鋼所受混凝土樓板反力近似均布荷載。當型鋼剛度不是特別大，且長度伸出設備較長，這時型鋼所受混凝土樓板反力情況：反力在荷載下方最大，同時沿遠離荷載方向逐漸減小、直至為零（荷載至該處距離即是型鋼荷載傳遞長度）；同時混凝土樓板對型鋼的反力在實際中應該是復雜多變的，為方便計算，假設段樓板反力為線性倒三角分布，如圖2所示。

2.3" 型鋼受力分析方法及模型簡圖

在房屋建筑工程結構設計中，常常要根據項目場地地勘報告中分析的地基地質情況，相應選擇可行且經濟的基礎形式進行基礎設計，其中連續基礎常會被采用。連續基礎包括單向或雙向通條設置于柱列或柱網之下的條形基礎和整片連續設置于建筑物之下的筏板基礎。對于柱下條形基礎內力分析方法一般有彈性地基梁法、倒梁法、剪力平衡法。對于筏型基礎內力分析方法一般有懸臂法、倒樓蓋法、柔性基礎簡化計算法、彈簧地基梁法、彈性理論截條法、彈性地基板法和有限元結構法等。本次我們研究用槽鋼轉換集中荷載的情況，主要是研究槽鋼的受力情況。若將設備荷載看成是房屋建筑中的豎向構件柱子，將型鋼看成條形基礎，將混凝土樓板看成地基；那么對型鋼的受力分析與對連續基礎受力分析就有很大相通之處；其中兩者主要區別僅是地基的模型不同。根據假設2：槽鋼與設備是固接，參考地基基礎反力分析的倒梁法[2]，采用倒置法將型鋼受力模型倒置后并根據對稱原理將計算簡圖進一步簡化。設備與型鋼為固接，型鋼受混凝土樓板反力為線性三角分布，長度為槽鋼荷載傳遞范圍，整體受力情況是一端剛接的懸臂梁受線性三角分布荷載，如圖3所示。

2.4" 型鋼撓度在倒置后計算模型中的反映

根據圖2，型鋼撓度最大值在設備荷載的正下方，為方便和簡化計算我們采用的模型簡圖如圖3所示，根據相對性平移后該撓度變為懸臂梁自由端的撓度。

3" 型鋼受力分析及荷載傳遞長度計算

3.1" 樓板受力后撓度確定

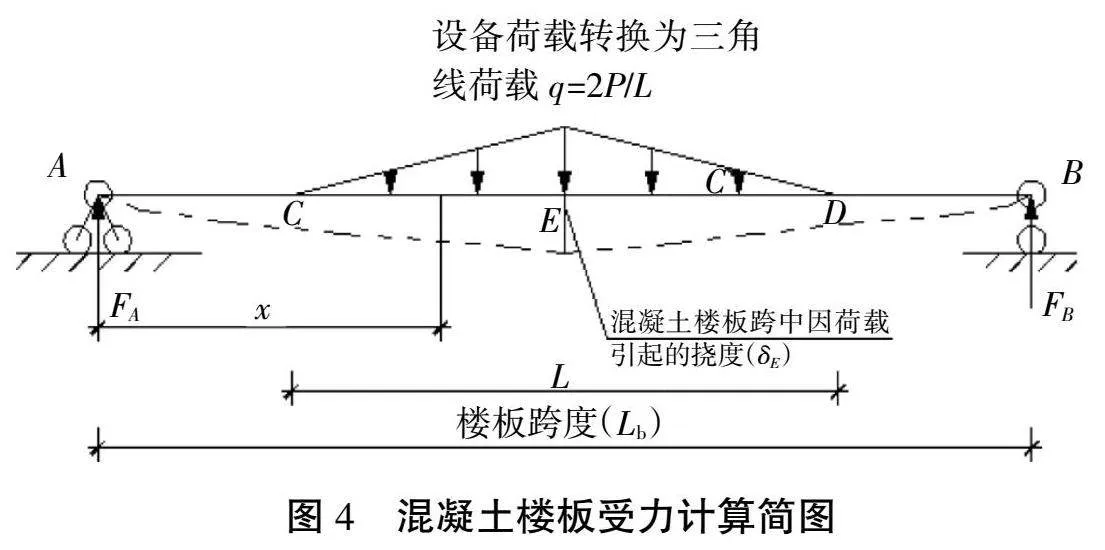
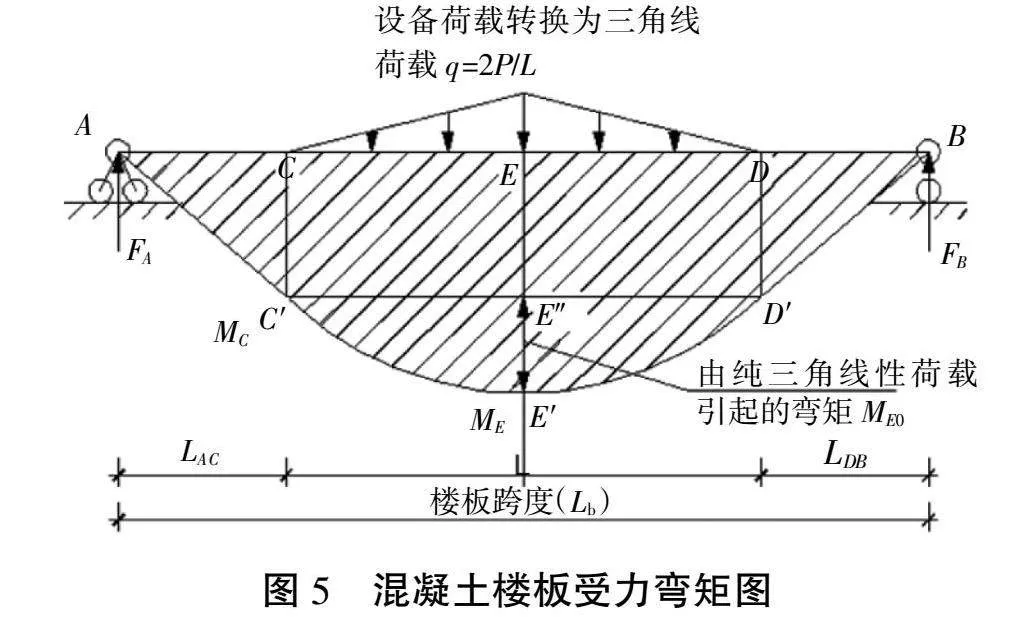
設備直接放置在混凝土樓板上時，設備在不同位置，對該板帶跨中撓度影響不同。本文為方便和保守計算，將設備布在最不利位置（樓板跨中），計算此時混凝土樓板跨中的撓度。當設備荷載通過型鋼轉換三角線荷載后，作用于混凝土樓板時，根據理論力學[3]中作用力與反作用力關系，可得樓板受力如圖4所示，此時計算模型為簡支梁跨中受三角線荷載，樓板主受力方向簡支在梁或圈梁上，支點分別為A與B，跨度為Lb；荷載在型鋼上傳遞范圍是CD段，長度為L；三角線性荷載為q；樓板跨中為E點，該點撓度為δE；支座兩端的反力分別為FA、FB。現根據結構力學[4]計算δE如下。

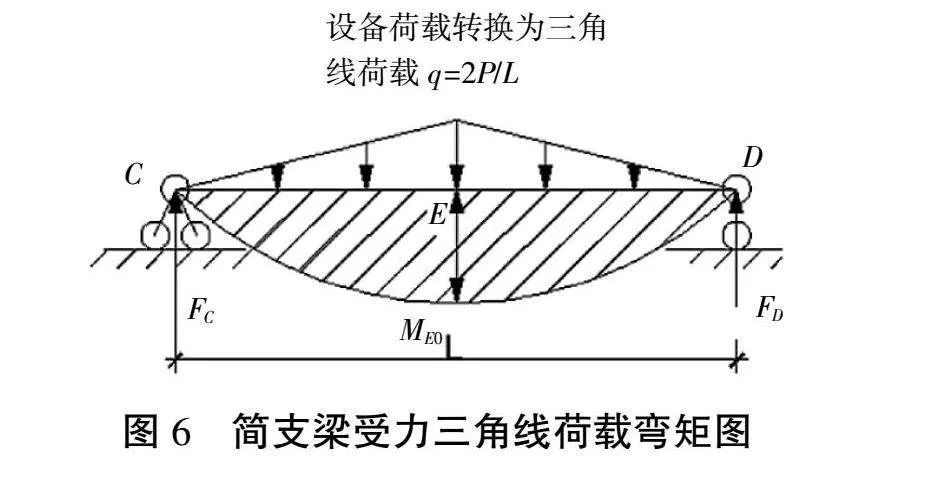
由計算簡圖易知：FA=FB==；MC=q；ME=Lq；對于CE段易知有AC段長度LAC=，Mx=x-q，顯然，CE段彎矩是三次拋物線。做彎矩圖如圖5所示，同時做出簡支梁受三角線荷載彎矩圖如圖6所示，易知有ME0=q。

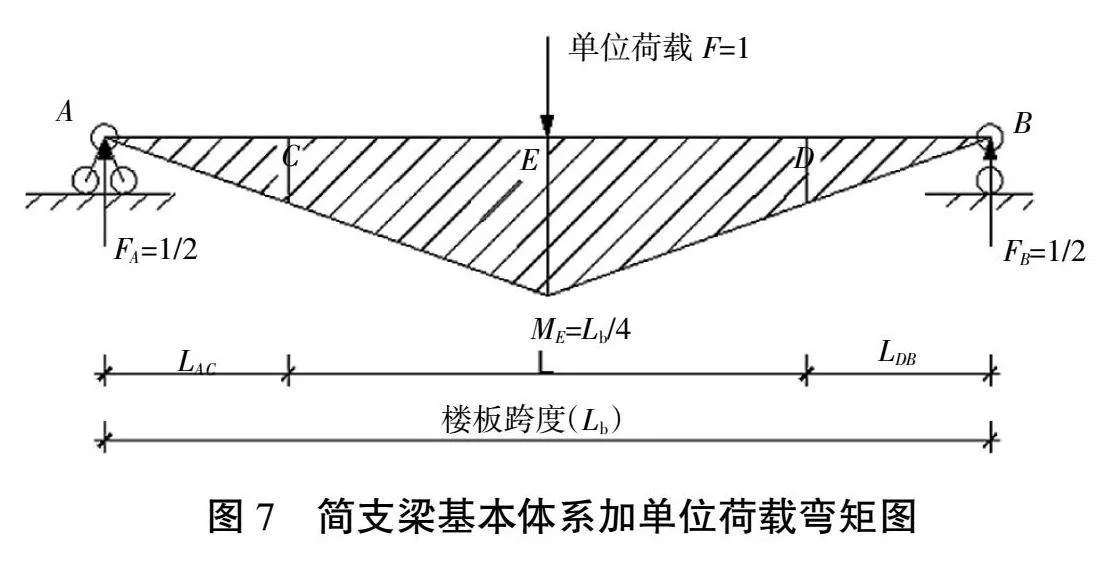
在將原混凝樓板視為簡支梁的基本體系中，在梁跨中E點加單位荷載 ，彎矩圖如圖7所示。

式中：大括內共由3項乘式相加。參看圖5，第1項是彎矩圖中三角形ACC′與單位荷載彎矩圖相乘結果；第2項是彎矩圖中矩形CC′E″E與單位荷載彎矩圖相乘結果；第3項是半拋物線圍成的CE′E″面積與單位荷載彎矩圖相乘結果。需要說明的是，半拋物線C′E′是三次拋物線，圖乘時所取面積和形心位置是按相應的系數計算。經對上式進行整理后得如下公式

E=q，（2）

式中：Eb為樓板混凝土彈性模量；Ib為板帶截面慣性矩，取1 m寬板帶計算。

3.2" 計算型鋼傳遞荷載距離

3.2.1" 計算型鋼受荷后撓度

根據圖3求得型鋼自由端的撓度[5]為

g=，（3）

式中：Eg 為型鋼彈性模量；Ig為型鋼截面慣性矩；q為混凝土樓板對槽鋼線性三角分布荷載最大值；L為型鋼荷載傳遞范圍長度。

3.2.2" 初步計算型鋼荷載傳遞距離

根據上述假設1，假設有g=E→=；進一步化簡為

L=Lb，（4）

從式（4）已經可以初步判斷出荷載在型鋼的傳遞距離與荷載大小無關，與型鋼剛度及樓板跨度正相關，與樓板剛度負相關。由于式（4）是假設樓板反力為線性倒三角分布，同時按假設混凝土板帶跨中布置最不利荷載計算板帶跨中撓度的初步計算結果，還需代入實例進行迭代驗算及修正，以取得較為貼近實際的結果。

3.2.3" 迭代驗算

在迭代驗算[6-7]過程中可以利用式（2）做變換得到方程1：L4-10LL+=0。這是一個非線性方程，其中L就是型鋼傳遞荷載的距離。同理式（3）做變換也可得到方程2：-30g Eg Ig=0。若方程1中Lb、Eb、Ib、δE1、q等已知，就可求出相應的L1，再將L1代式（3），求出相應的δg1，對δE1與δg1進行比對，若差值較大，再將δg1賦值于δE2，在其他參數不變情況下，用δE2代入方程求出L2代入式（3），求出δg2，再對δE2與δg1進行比較。當δEx與δgx比較接近時，所求的Lx就是目標值。方程1的初始值δE1可采用設備集中荷載混凝土樓板板帶中央，按簡支梁受跨中荷載算出δE1=。

3.2.4" 模擬實例進行初步測算及分析

給定一個電信機房型鋼加固條件：加固型鋼選25C號槽鋼[8]；混凝土樓板厚100 mm，強度等級[1]為C30，板帶寬取1 000 mm。經查，Eg=200 GPa，Ig=3 690 cm4；Eb=30 GPa，Ib=8 333 cm4。將參數代入式（4）可得

L=1.813 21 Lb。（5）

槽鋼對荷載傳遞長度是樓板跨度1.81倍左右，可近似認為槽鋼對荷載的傳遞長度是沿槽鋼全長，荷載分布形式近似均布線荷載。由式（5）可知，正常條件下，型鋼對荷載傳遞范圍遠大于樓板的跨度，可初步判斷是由于型鋼剛度遠大于混凝土樓板的剛度，造成原先保守估計型鋼受荷后變形撓度與樓板變形撓度一致的假設在通常情況下不成立。因此無需再進一步迭代驗算就基本可得出結論：通常條件下通過型鋼轉換集中荷載時，型鋼對荷載的傳遞長度是沿型鋼全長，荷載分布形式近似均布線荷載。

4" 型鋼轉換荷載后對樓板彎矩、撓度的影響

4.1" 設備直接放置在混凝土樓板上且荷載布置在最不利位置時的跨中彎矩及撓度

根據3.1，此時按簡支梁跨中受集中荷載，易得混凝土樓板跨中彎矩[5]

MC1=，（6）

式中：MC1為樓板跨中C點彎矩；Lb為樓板計算跨度；P為設備荷載。樓板跨中撓度[5]為

δC1=，（7）

式中：δC1為樓板跨中C點撓度；Eb為樓板混凝土彈性模量；Ib為板帶截面慣性矩，取1 m寬板帶計算。

4.2" 設備通過型鋼改變荷載傳遞方式后（變為均布線荷載）樓板跨中彎矩及撓度

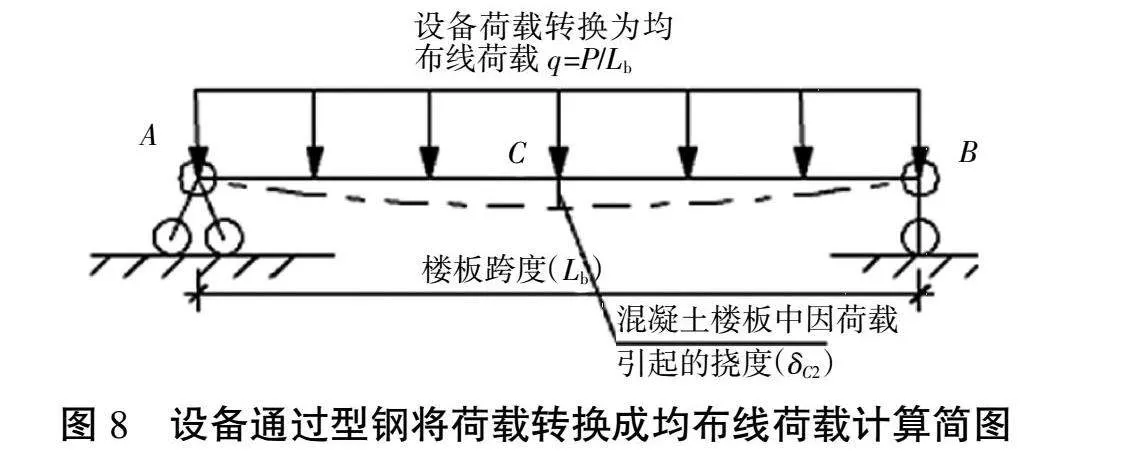
設備通過槽鋼將荷載轉換后再放置在混凝土樓板上，此時樓板跨中彎矩和撓度按簡支梁上布均布線荷載計算，如圖8所示。易得混凝土樓板寬中彎矩[5]為

MC2=，（8）

式中：MC2為樓板跨中C點彎矩。樓板跨中撓度[5]為

δC2=，（9）

式中：δC2為樓板跨中C點撓度。

由于P=qLb，代入式（8）、式（9）可得

MC2=，（10）

δC2=。（11）

4.3" 型鋼轉換荷載形式后情況分析

用型鋼將荷載轉換形式后樓板跨中彎矩及跨中撓度與設備直接布置在樓板上時相應的彎矩及撓度進行比較，如下

從式（12）、式（13）可以看出，通過型鋼將設備集中荷載轉換成線荷載后，混凝土樓板跨中最大彎矩減小1/2；撓度減小3/8。

4.4" 型鋼轉換荷載形式應用時需注意的方面

1）對采用型鋼轉換超重設備荷載形式時，每個結構單元所布置的設備總重不能超過原結構單元的設計總荷載。

2）在結構單元布置荷載時，型鋼長度方向盡量沿結構單元主受力方向布置。

3）在結構單元布置荷載時，空間允許的情況下，可以布置多排的盡量多排布置，有利于分散荷載且增加受荷面積。

5" 結論

1）通過假設型鋼受力產生微小形變，與樓板混凝土形變滿足變形協調條件，樓板形變產生的撓度與型鋼形變產生的撓度一致；假設型鋼與設備為固接，建立了計算模型并進行分析。確定了型鋼傳遞荷載長度與混凝土樓板跨度之間數量關系，明確了荷載在型鋼的傳遞距離與荷載大小無關，與型鋼剛度及樓板跨度正相關，與樓板剛度負相關。同時通過模擬實際應用，明確了通常情況下，采用型鋼改變荷載傳遞方式，可近似認為型鋼對荷載的傳遞長度是沿型鋼全長分布，荷載分布形式近似均布線荷載。

2）依據前文3.2.2的結論，對設備直接放置樓板及通過型鋼改變荷載傳遞方式后2種情況的樓板跨中彎矩及撓度分析對比，發現通過型鋼改善混凝土樓板承載力是可行和有效的。

3）雖然本次研究中依據所建模型和假設推出的式（4）在通常情況用于分析型鋼加固既有混凝土樓板用處不大，主要是由于型鋼剛度與樓板的剛度差距較大，型鋼幾乎是沿通長傳遞荷載。但當型鋼放置的樓板為剛度較大且與型鋼剛度相近的結構單元時，式（4）還是可用于結構分析。

參考文獻：

[1] 程文瀼，康谷貽，顏德姮，等.混凝土結構[M].北京：中國建筑工業出版社，2001.

[2] 楊位洸.地基及基礎[M].北京：中國建筑工業出版社，1999.

[3] 趙經文，王鐸.理論力學[M].北京：高等高等教育出版社，1997.

[4] 龍馭球，包世華.結構力學教程[M].北京：高等教育出版社，2002.

[5] 孫訓方，方孝淑，關來泰，等.材料力學[M].北京：高等教育出版社，1998.

[6] 李慶揚.數值分析[M].北京：清華大學出版社，2008.

[7] 譚浩強，田淑清.FORTRAN77結構化程序設計[M].北京：清華大學出版社，1998.

[8] 陳紹蕃.鋼結構設計原理[M].北京：科學出版社，2005.