觀察·想象·推理：幾何學習三部曲

第5章走進幾何世界

領"銜"人：朱月紅（江蘇省特級教師）

組稿團隊：江蘇省泰州市高港區朱月紅初中數學名師工作室

“走進幾何世界”屬于幾何的研究范疇。對于剛上初中的同學來說，初中的幾何知識既熟悉又陌生。與小學相比，初中幾何知識更系統，更考驗我們的觀察力、想象力和邏輯推理能力。今天，就讓我們一起踏上這場充滿樂趣與挑戰的幾何學習之旅吧。

觀察——開啟幾何世界的鑰匙

數學是研究數量關系和空間形式的學科。當我們環視四周，不難發現其中隱含著豐富多彩的幾何圖形。教室里的門窗、課桌的形狀；路邊建筑物的輪廓，樹木的排列；同學們手中的乒乓球、魔方等日常物品，都可以抽象成我們熟悉的幾何圖形。這些圖形構成了幾何研究的對象，包括圓柱、圓錐、正方體、長方體、球體等，以及構成這些幾何體的基本元素：點、線、面。

在將現實世界中的物體抽象為幾何圖形，并確定基本幾何元素之后，我們不禁會問：有了研究對象，接著研究什么？怎么研究？事實上，我們有了基本元素（研究對象）后，一般要研究元素之間的關系。比如，當我們觀察三棱柱、四棱柱等幾何體時，會研究每個幾何體的頂點數、棱數、面數，以及它們之間的數量關系，探索其中的規律。如下頁圖1，如果我們從正方體中切去一個角，我們要研究的問題是：有哪些切法？每一個幾何體頂點數、棱數、面數之間有什么關系？有什么規律？通過自主探索，同學們有什么發現呢？這可是著名的歐拉公式哦！

想象——翱翔于幾何的藍天

如果說觀察是打開幾何世界大門的鑰匙，那么想象就是讓我們自由翱翔在這片藍天中的翅膀。幾何學習不是紙上談兵，我們需要發揮想象力，將抽象的概念轉化為生動的圖形，甚至創造出新的圖形組合。

動起來，更精彩。圖形的運動包括平移、旋轉和翻折。大家不要小看這三種運動哦，在后續學習中，很多幾何運動都離不開它們呢。通過展開與折疊，我們還會學習常見立體圖形的平面展開圖，同時，也會接觸將展開圖還原成立體圖形等實踐知識。因而，立體圖形可以轉化成平面圖形，平面圖形也可以轉化成立體圖形。

如圖2，長方體的長為15，寬為10，高為20，點B離點C的距離是5，一只螞蟻如果要沿著長方體的表面從點A沿直線爬到點B，有幾種走法？

數學中，數和形也可以互相轉化。比如：求[12]+[14]+[18]+[116]的和，如果將這個式子與圖3結合起來，是不是更簡潔？（答案：[12]+[14]+[18]+[116]=1-[116]=[1516]）

推理——攀登幾何的高峰

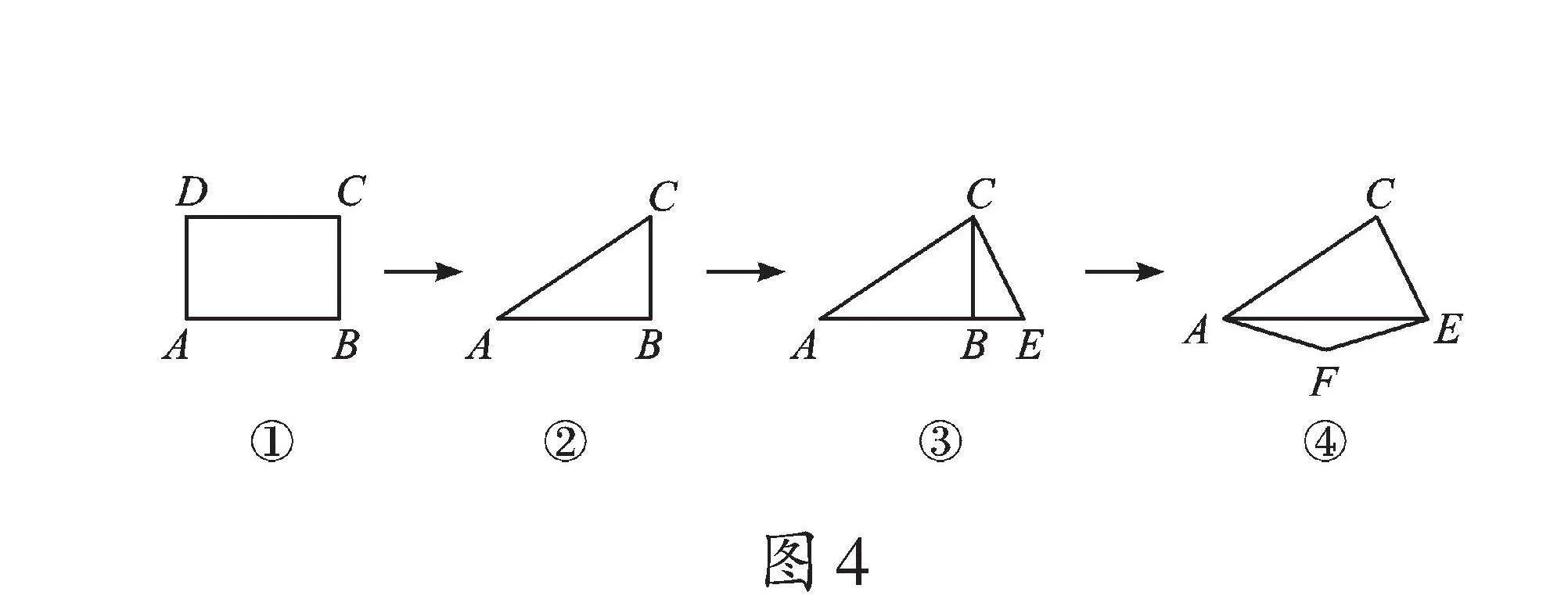
幾何學習不僅僅是觀察和想象的結合，它更離不開嚴謹的邏輯推理。我們可以從已知條件出發，通過推理，一步步得出未知的結論，感受數學邏輯的力量和美感。特別需要注意的是，我們在幾何學習中，對任何一個研究對象，都要掌握三種語言——“文字語言、圖形語言、符號語言”，要將三者結合起來整體學習。如“三角形”，它的文字語言是“在同一平面內，由不在同一直線上的三條線段首尾順次連接組成的圖形叫三角形”，圖形語言是下頁圖4②，符號語言是“△ABC”。在語言規范描述的基礎上，還要注意解題過程的完整，即推理要嚴謹。如：長方形ABCD的4個角都是90°，根據圖4的思路，你能得到一般四邊形的內角和嗎？

解：因為長方形ABCD內角和為360°（已知），所以直角△ABC內角和為180°。

因為△ABC與△BCE的內角之和為360°（圖4③），∠ABC+∠CBE=180°，所以△ACE的內角和為180°。

所以四邊形ACEF的內角和為360°（四邊形可分成任意兩個三角形）。

這種解決問題的過程其實就是推理的過程。我們通過觀察和想象，發現現實世界中的幾何圖形及其特征、關系、規律，提出問題與猜想，通過推理得到一般結論。

“走進幾何世界”為我們拉開了幾何學習的序幕。如果我們想繼續研究，就必須在此基礎上深入研究平面圖形，最終才能全面認識立體圖形，為高中階段要學習的立體幾何打下基礎。相信同學們經過自己的努力，一定能夠在幾何學習中學出樂趣，學出成就。

（作者單位：江蘇省泰州市環溪初級中學）