外壁非對稱填土荷載對內支撐式敞口隧道結構內力的影響研究

針對大跨內支撐式敞口隧道結構，文章采用有限元分析方法，系統研究了單側壁板外無填土及不同填土高度下的結構受力機制。結果表明：在單側壁板外無填土工況（工況A）下，結構的彎矩分布與外壁雙側均衡土壓工況（工況B）相比，呈現顯著差異；若其余條件不變，從工況B改變至工況A，工況A無填土側的壁板根部、底板柱腳及其附近區域受到較大影響；若依據工況B設計的結構，在左右填土不均時則可能因受力配筋不足而受損。因此，施工回填中需嚴格控制左右填土高差，以減小結構板各區域的彎矩極值，并降低柱對底板彎矩的影響；在兩側壁板外存在顯著不平衡土壓時，建議在柱腳附近采取結構加強措施。基于研究結果，按雙側均衡土壓工況設計的內支撐式敞口隧道更具經濟性。同時，建議填筑高度低的一側填土與另一側壁板外填土的高差≤0.6倍壁板計算高度，以避免壁板彎矩方向發生突變。

公路隧道；結構設計；有限元分析；支撐式隧道；彎矩計算

U456.2A311065

作者簡介：

謝明志（1978—），高級工程師，主要從事公路、市政道設計及管理工作。

0" 引言

在城市地下交通建設中，淺埋隧道結構的設計扮演著至關重要的角色。傳統的懸臂式U形槽結構在面臨底板埋深大、側墻懸臂高的挑戰時，常因結構厚度過大而面臨經濟性的限制。為解決這一問題，梧州某道路工程隧道在設計上創新性地引入了內支撐式敞口隧道結構，旨在通過優化結構受力分布，實現更為經濟合理的建設方案。這種設計顯著減小了結構底板和側墻的彎矩與剪力，從而允許使用更薄的板墻厚度，有效降低了工程成本。然而，內支撐、腰梁和立柱的增加也使結構的受力狀態變得更為復雜。從計算分析模型角度，由平面應力狀態轉變為三維空間受力狀態，增加了結構內力計算的難度和復雜性。因此，如何高效、準確地分析內支撐式敞口隧道結構的內力，為工程設計提供科學指導，是一個亟待解決的問題。

在隧道結構分析領域，有限元法因其在處理復雜結構受力問題時的高效率、高精度和廣適用性而備受青睞［1-6］。鄒濤［7］利用Autodesk Robot Structural Analysis軟件，針對隧道頂板開洞的影響進行了深入研究，并探討了橫梁布置方案對結構的影響。陳衛軍［8］和代坤［9］也分別通過有限元模擬，研究了半敞口隧道開洞和地鐵車站結構的受力特性，進一步驗證了有限元法在隧道結構分析中的有效性。特別是代坤的研究，通過三維與二維有限元模型的對比，揭示了平面模型的局限性，強調了三維模型在復雜結構分析中的必要性。

本文以梧州某道路工程隧道結構為研究背景，利用有限元軟件對內支撐式敞口隧道結構進行數值模擬計算。先擬定單側無填土工況進行計算分析，接著將單側填土高度從0 m開始逐步地增加后計算分析。旨在探究在單側填土至頂前提下，隧道外壁兩側不同高度的填土產生的非對稱填土荷載對隧道結構內力的影響規律。研究成果將為今后類似工況下的內支撐式敞口隧道結構設計提供參考。

1" 工程概況

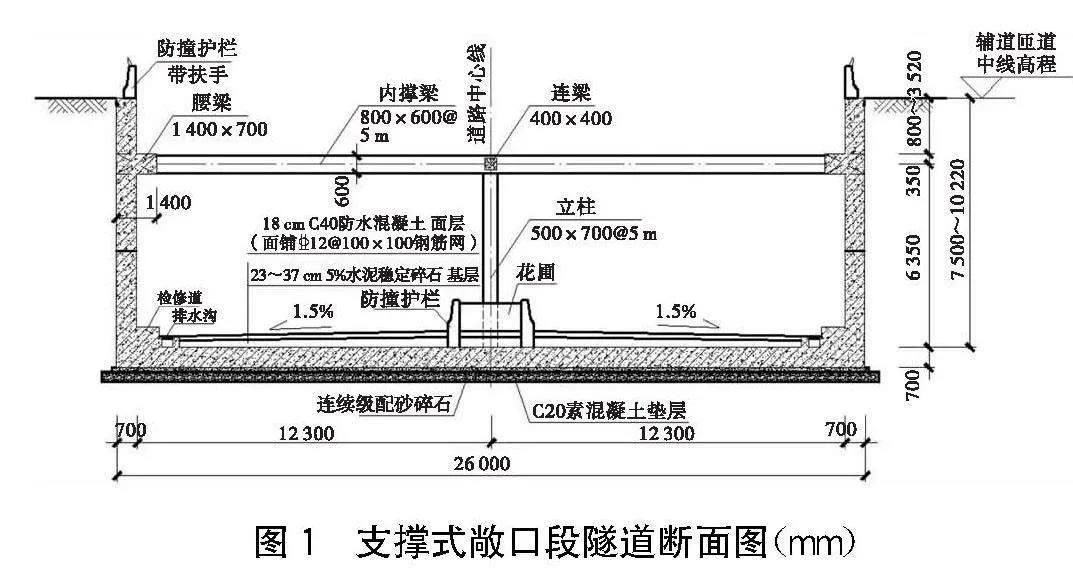
梧州某道路工程為城市主干路，其設計全長達到4.613 km。該工程中包含下沉式隧道，為優化工程投資成本，其中敞口段隧道采用了內支撐式U型槽結構，如圖1所示。該結構總長353.18 m、外寬26 m，目前已完成結構施工但尚未進行填土。基于實際需求，計劃先進行單側外壁填土至頂部，并暫時恢復該側頂部路面的交通。為實現這一目標，需分析在原結構設計方案下，單側無填土工況與雙側土壓平衡工況之間的內力差異；進一步探討在單側外壁板填土至頂部的條件下，另一側外壁不同填土高差對結構內力的影響規律。

2" 模型構建

2.1" 模型的建立

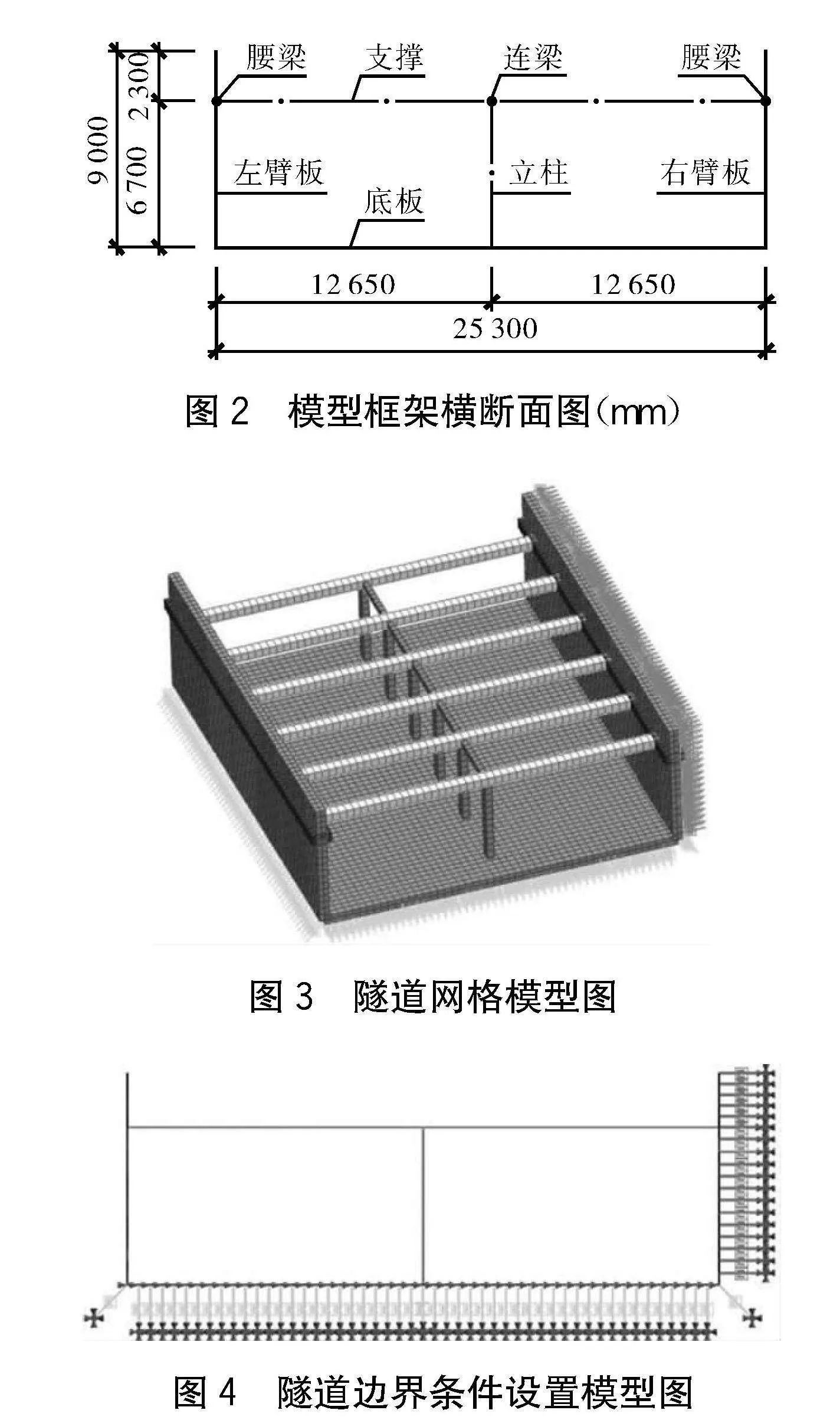
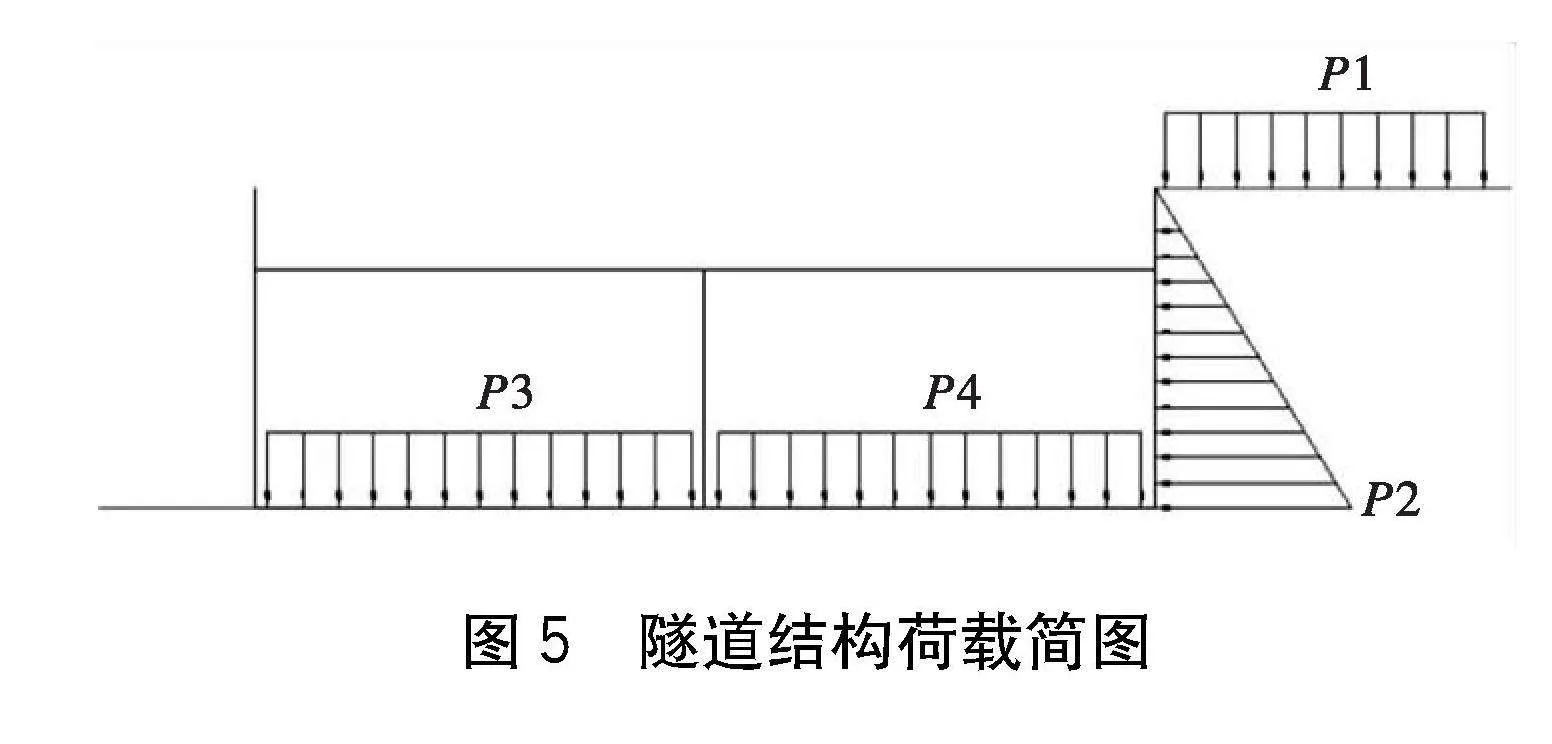
采用Midas GTS NX軟件，對支撐式敞口段隧道進行模型構建，其中隧道結構混凝土標號為C35，本構模型采用“彈性”模型，彈性模量設置E=3.15×104 MPa，重度γ=25 kN/m3，泊松比μ=0.2。隧道壁板采用“2D板單元”模型模擬，支撐采用“桁架”模型模擬，腰梁和立柱采用“梁單元”模型模擬，底板、壁板與土接觸側設置“土彈簧”連接；基底摩擦作用以限制TX向位移形式模擬。隧道節段長度為L1=30 m，前后腰梁懸挑2.5 m，支撐間距5 m，計算左右壁板高取h=9 m，底板計算跨度取L=25.3 m；計算模型框架橫斷面、網格模型及邊界條件設置分別如圖2～4所示。

外壁非對稱填土荷載對內支撐式敞口隧道結構內力的影響研究/謝明志

2.2" 工況設置

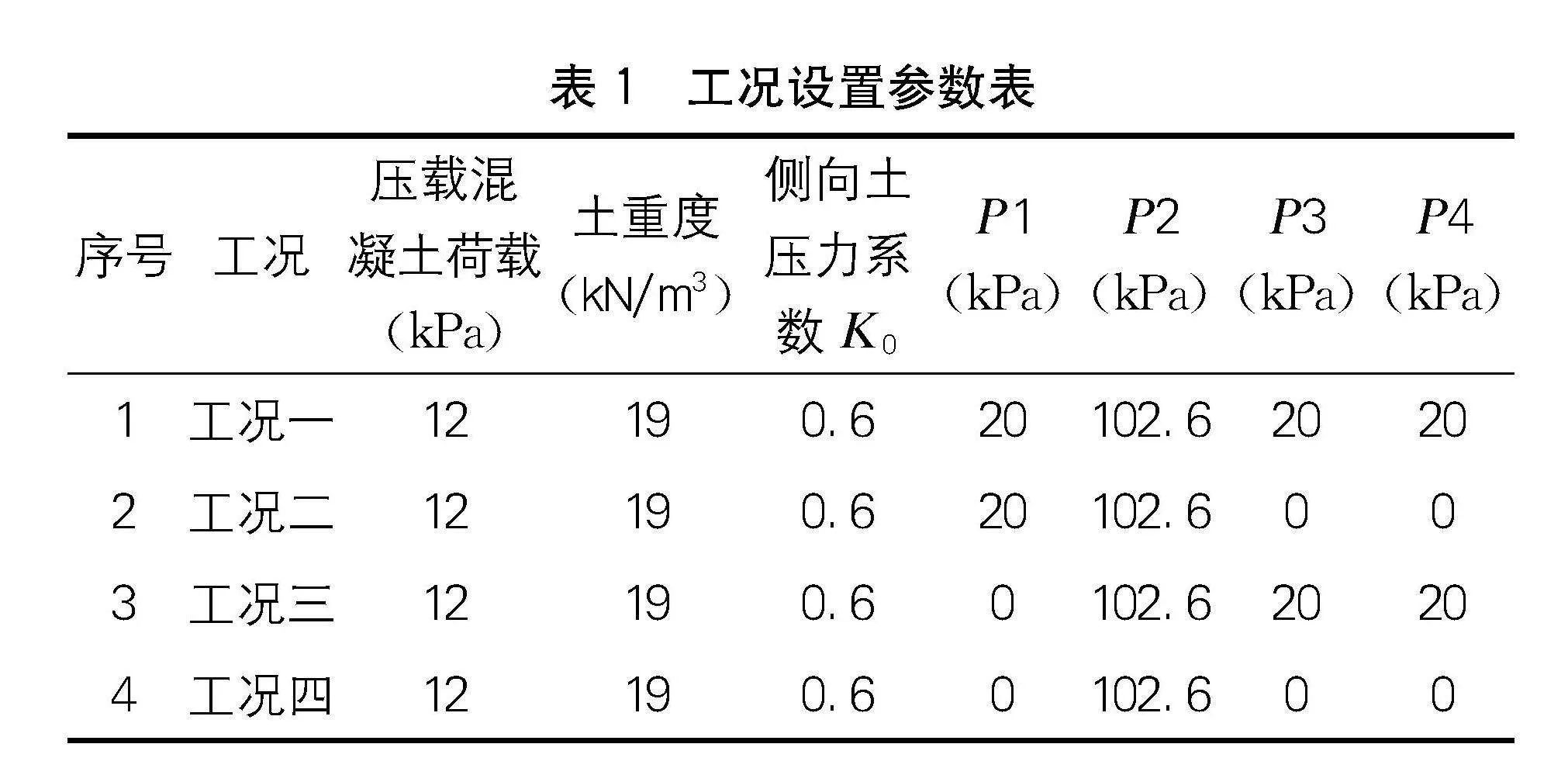
隧道結構所受到的荷載歸結如下：結構外側填土頂車輛荷載經填土傳至外壁板的側向壓力P1、外壁填土本身自重引起的側向土壓力P2、隧道內車輛對底板的荷載P3和P4。

為更全面地對隧道結構的不同受力狀態下內力分布的情況和規律進行分析，現依據隧道結構的受力狀態劃分為四個典型工況。

工況一：隧道內和右外壁頂地面皆有車載。

工況二：隧道內無車載，右外壁頂地面有車載。

工況三：隧道內有車載，右外壁頂地面無車載。

工況四：隧道內和右外壁頂地面皆無車載。

各類荷載情況如圖5所示，具體工況設置見表1。

3" 模型計算結果及分析

3.1" 典型計算斷面選取

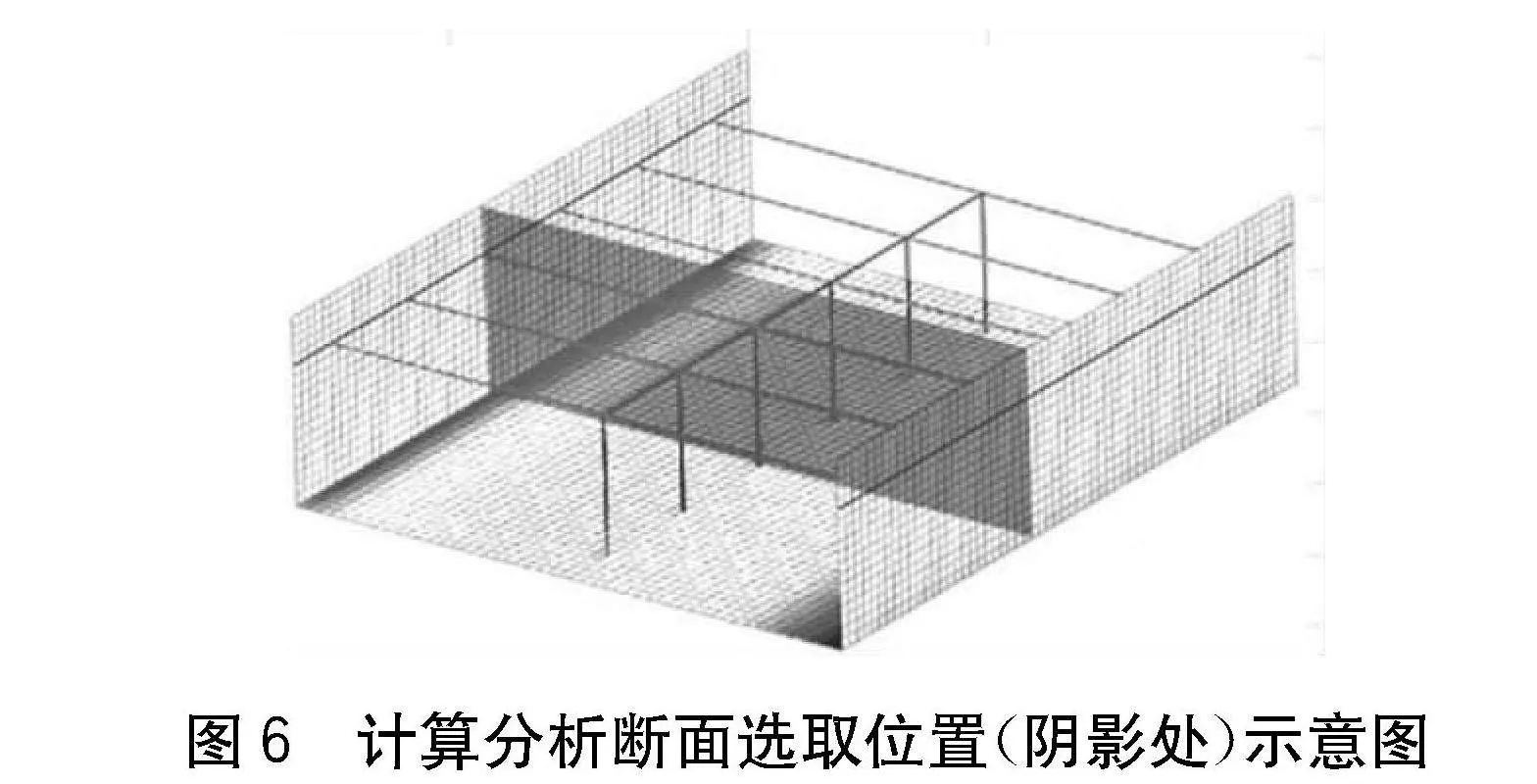
該敞口段隧道底板和壁板彎矩橫向最大數值約為縱向的5倍，故該結構的橫向為主受力方向。考慮特殊性，本文選取的計算橫斷面位于隧道節段支撐處，具體如圖6所示。

3.2" 外壁單側填土和雙側填土壓力均等工況的隧道結構變形趨勢

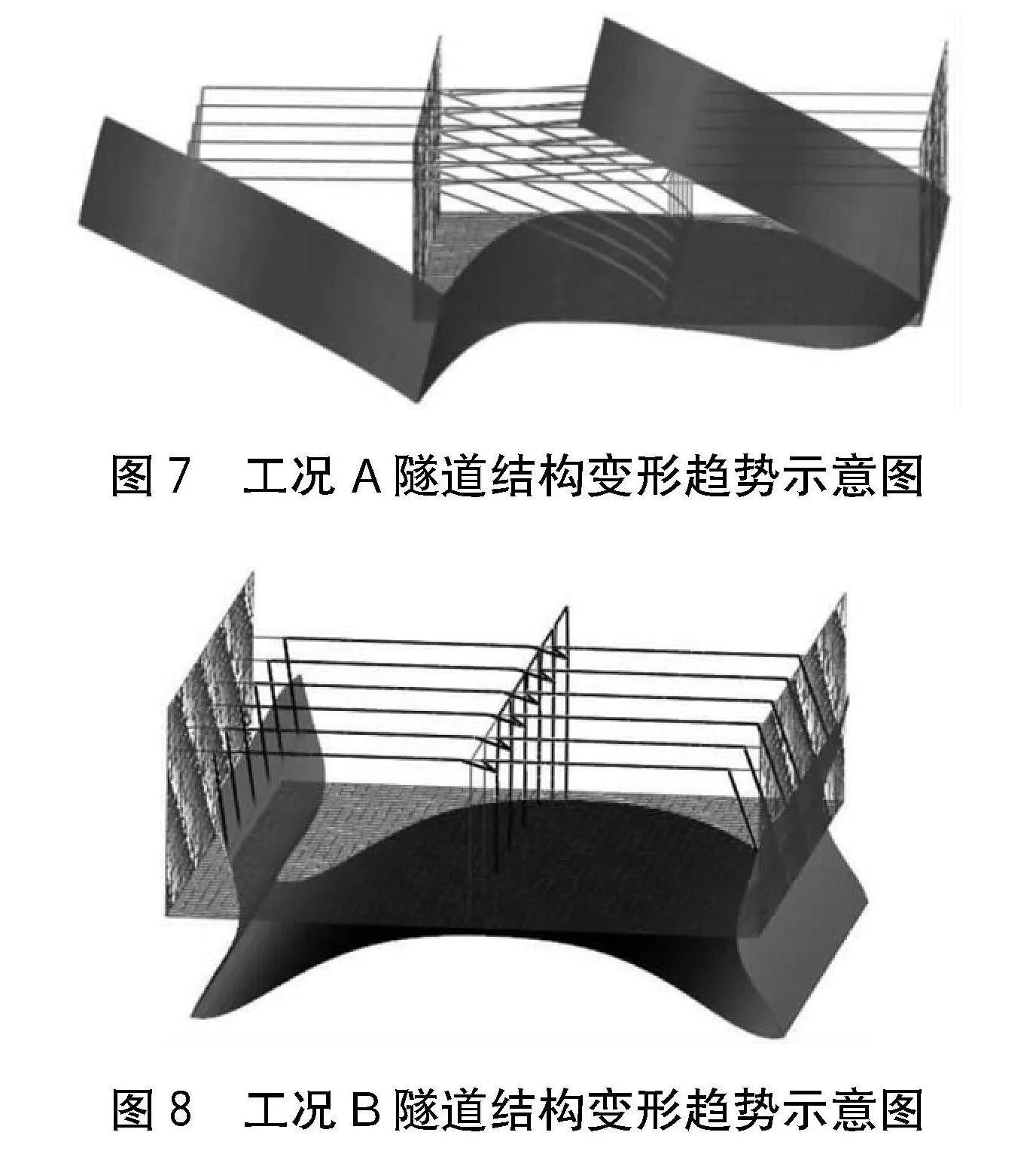
分別建立相同工況下隧道結構單側壁板外無填土工況（工況A）、外壁雙側均衡土壓工況（工況B）模型計算，得出隧道結構的變形狀態分別如圖7和圖8所示。

由圖7可知，工況A時，由于內支撐式敞口隧道左右壁板外側土壓不平衡，故兩壁板有向左變形的趨勢，且彎矩方向基本一致；底板中間凸起部分往柱左側（無填土側）移動。

由圖8可知，工況B時，隧道結構左右變形對稱，底板跨中凸起，壁板于腰梁和根部之間往內側凸起。

3.3" 各工況斷面處底板和壁板彎矩計算結果分析

在隧道結構單側（左側）外壁無填土情況下，對上述各荷載工況進行計算，得出彎矩云圖如圖9所示（圖9僅為工況一，其余工況趨勢類似，故不在此列出）。

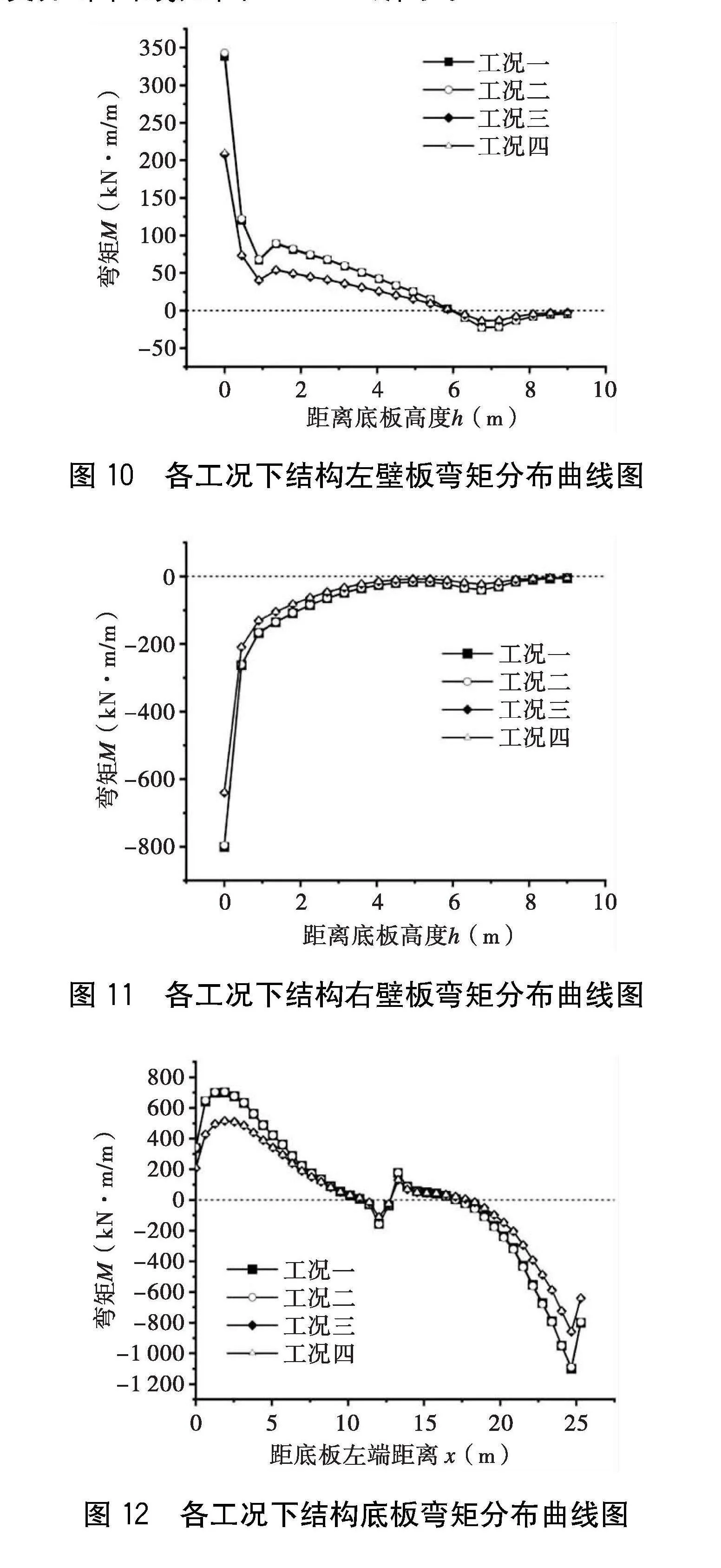
整合計算斷面處各工況下外壁板彎矩分布情況，其沿高度分布曲線如圖10～12所示。

由圖10～12可知，工況一和工況二對應的曲線基本重合，工況三和工況四對應的曲線基本重合，因此隧道內車輛荷載P3和P4對隧道結構彎矩影響較小，最不利工況為工況一或工況二，即右路面存在車輛荷載P1時。

3.4" 外壁單側無填土對隧道結構計算斷面處彎矩的影響

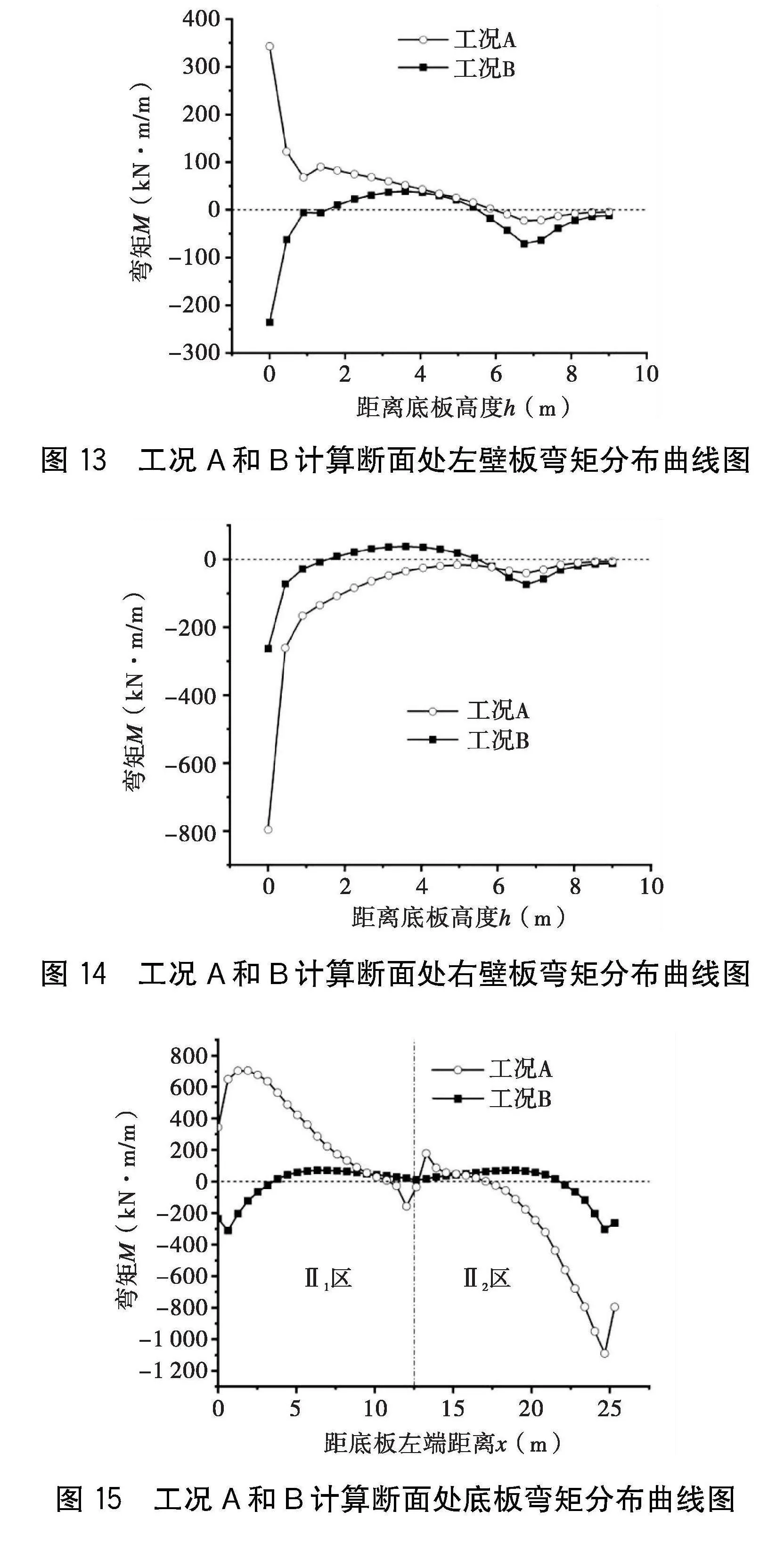
根據上述分析，選取最不利的工況二再用相同方式建立結構外壁雙側均衡土壓模型，選取上述計算斷面，得出其彎矩分布圖如圖13～15所示。其中，隧道結構外壁板單側無填土工況為工況A，外壁雙側均衡土壓工況為工況B。

圖13顯示，工況A和B在左壁板上半部分的彎矩變化趨勢相似；工況A相較于工況B，壁板上半部分反彎點上移，支撐位置的彎矩最大值減少了67.8%。

左壁板下半部分，工況B出現反彎點，中部區域內側受拉，而根部區域外側受拉；工況A則無反彎點，且內側全為受拉區。

兩種工況在左壁板根部彎矩均為最大，但工況A的彎矩絕對值是工況B的約1.46倍。因此，工況A對于壁板根部區域彎矩影響最大，受拉壓方向存在調轉現象，若隧道初始時按雙側有均衡土壓設計，一旦工況改變（變為壁板單側無填土），則受拉區存在配筋不足的風險。

對于右壁板，圖14顯示工況B中下部為正彎矩，根部反彎點位于（0.15～0.2）h（h為總壁高）；而工況A相較于工況B，彎矩方向基本一致，支撐位置負彎矩減少45.8%，但根部負彎矩約增大至工況B的3倍。

由圖15可知，對于結構底板，工況B彎矩曲線相對于中軸線對稱，近似馬鞍形，靠近壁板區為負彎矩，其余則為正彎矩，且于柱點處數值減小至接近零；工況A條件下，彎矩曲線近似相對于中心點對稱，且于柱點附近突變明顯，Ⅱ1區除柱腳附近，其余皆為正彎矩，且底板端部達到最大值；Ⅱ2區則相反，且同樣在底板端部彎矩最大，但該區彎矩最大絕對值是Ⅱ1的1.55倍。Ⅱ1區在工況A下，彎矩最大值相對B工況往端部方向移動，數值是工況B的約10倍；Ⅱ2區在工況A下反彎點往左移，且負彎矩最大值是工況B的約3.6倍。工況A相較于工況B，底板受拉區位置發生改變，對于底板上側受拉區，Ⅱ1區往左擴大，Ⅱ2區往左縮短；對于底板下側受拉區，Ⅱ1區僅在柱腳附近受拉，Ⅱ2區端部的受拉區往左擴大。由此可得，結構外壁僅有單側填土相較于兩側均衡填土壓力條件，對于底板的拉、壓狀態和內力數值大小影響很大，且敏感度最大；彎矩極值變化明顯，特別是按原受拉、受壓區分別配置鋼筋，一旦工況轉變為僅有單側外壁填土，則板的受拉、受壓區彎矩大小及位置發生重大改變，很容易發生配筋不足現象。

3.5" 隧道單側填土至外壁頂條件下另一側不同填土荷載對計算斷面結構彎矩的影響

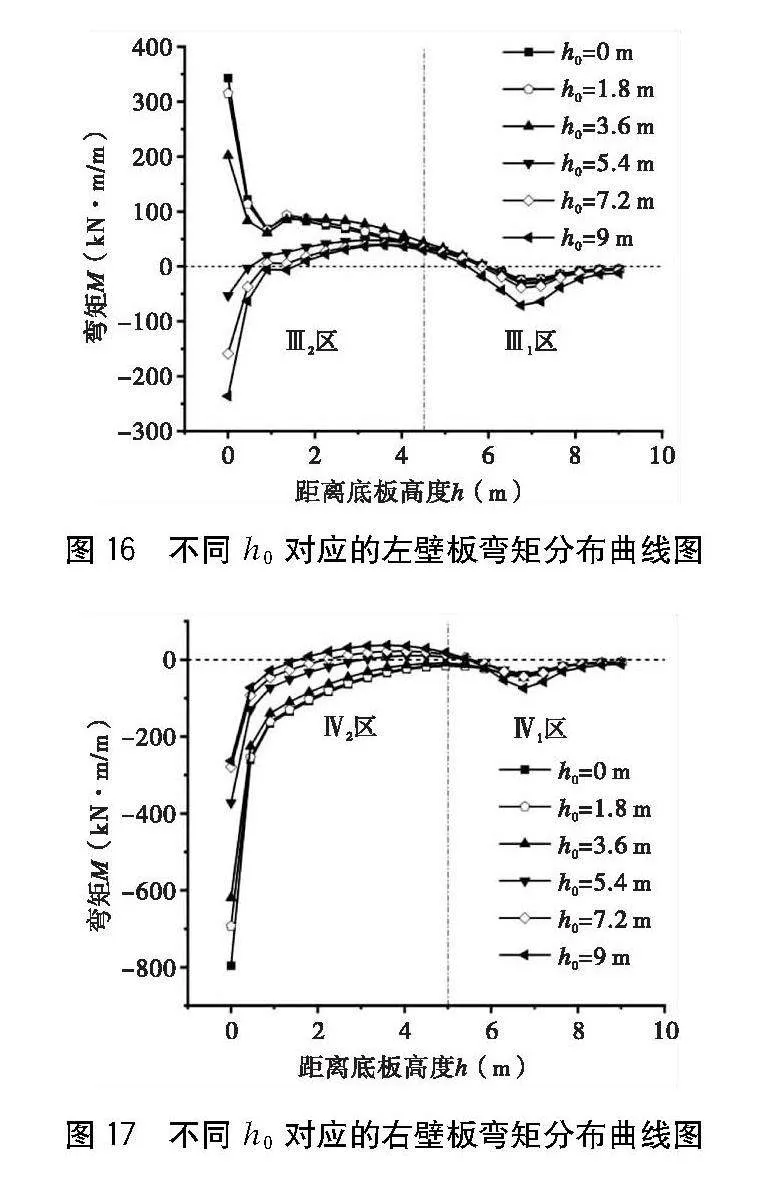
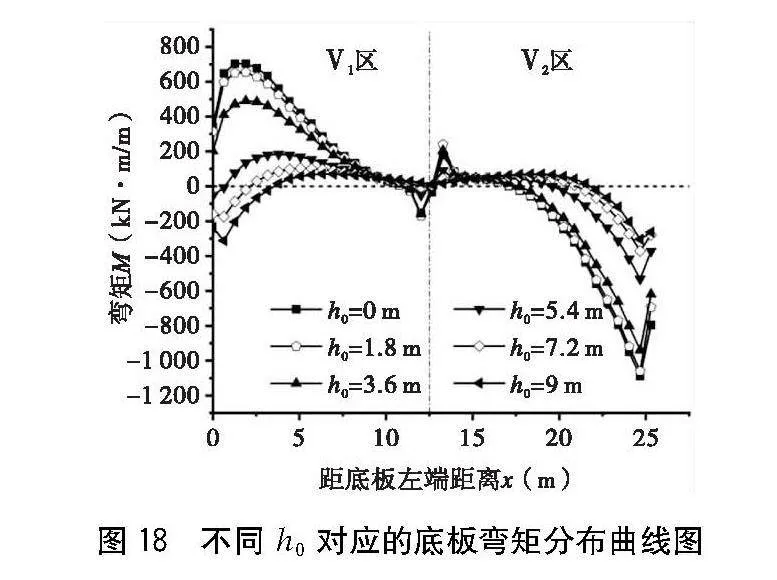
在隧道右側外壁填土至頂情況下，就左側外壁不同高度h0填土產生的荷載對彎矩的影響進行分析，選取最不利的工況二采用上述相同方式建立計算模型，得出其彎矩分布分別如圖16～18所示。

針對左壁板，設定其計算高度為h。由圖16可知，當左壁外側填土高度h0≤3.6 m（即0.4h）時，左壁板的受力狀態表現為上部彎矩為負值（即壁板外側受拉），而中下部彎矩為正值（即壁板內側受拉）；反彎點位于Ⅲ1區，且隨h0增大，其位置基本不變，大致位于（2/3）h處；Ⅲ1區彎矩極值位于支撐點處，其隨h0遞增而增加，增加速率為+2.44 kN·m/m。當左壁外側填土高度h0＞3.6 m（即0.4h）時，左壁板的受力狀態發生顯著變化。此時，壁板中部的彎矩變為正值（即壁板內側受拉），而其余部分的彎矩為負值（即壁板外側受拉）。正彎矩在壁板中部、負彎矩在壁板根部達到極值。負彎矩極值隨h0遞增而增加，增加速率為+50.72 kN·m/m，正彎矩極值則隨h0遞減而減小，減小速率為-2.53 kN·m/m。由此可知，h0的增加，對左壁板根部彎矩（數值和方向）影響最大，當填土≤0.4h時，壁板根部內側受拉，方向突變點位于0.4～0.6h，當h0大于突變點則壁板根部受拉區變為外側；當h0小于突變點時，隨著h0增加，根部受拉區彎矩減小；當h0大于突變點時，隨著h0增加，根部受拉區彎矩增大。

由圖17可知，對于右壁板，支撐點和壁板根部彎矩分別達到Ⅳ1區和Ⅳ2區的極值，隨著h0遞增，二者的比值由19.76降至3.53，即支撐點和壁板根部彎矩差異隨h0的增加而減小。當h0≤3.6 m（0.4h）時，皆為負彎矩（壁板外側受拉）；當h0＞3.6 m（0.4h）時，Ⅳ2區出現正彎矩（壁板中下部內側受拉），且反彎點隨h0增大而右移，根部負彎矩極值隨h0遞增而減小。由此可知，隨h0增大，根部受拉區方向不變，配筋率可大幅度減小；當h0＞0.4h～0.6h時，壁板內側存在受拉區，該區應適當按受拉配筋。

由圖18可知，對于底板，隨h0增大Ⅴ1區和Ⅴ2區彎矩極值位置逐步往中軸線移；Ⅴ1區彎矩極值逐步減小，Ⅴ2區曲線逐步往上拱；兩區域彎矩曲線逐步趨于隧道中軸對稱；柱對跨中部彎矩曲線的影響也逐步弱化。

綜上分析知，隨左壁外側填土高度h0增加，隧道壁板和底板結構彎矩分布也逐步趨于對稱，以結構中軸線為參照，左半區與右半區壁板彎矩差異逐漸減小，各區域的極值逐步降低；當左填土高度＞0.4h時，壁板彎矩方向及分布規律基本跟左右對撐填土工況相差不大，故為保障結構受力穩定性，左壁與右壁外側填土高差宜≤0.6h。

4" 結語

通過對支撐式敞口段隧道結構的有限元建模分析，本研究得出以下結論及建議：

（1）對比工況A和工況B，壁板和底板彎矩的分布規律和拉壓狀態基本不同，彎矩曲線近似關于柱腳點中心對稱；無填土側的壁板根部內側受拉，外側受壓，另一側壁板則相反；基于上述內力分布機理可知，若原結構按工況B的受力需求設計配筋，且無足夠的安全裕量，先填一側土，另一側保持無填土狀態，則結構易發生破壞。

（2）對于工況A，底板彎矩影響最大點位于柱腳點附近，其兩側彎矩方向相反，且差值明顯。

（3）結構外壁工況A情況下的隧道結構板彎矩極大值位置一般位于板端部，且數值比工況B大幅增加，由此對結構厚度或配筋的需求也大幅增加。反之，工況B條件下結構板厚度和配筋需求較小，更經濟、合理。

（4）對于結構右側外壁填土至頂的工況前提下，隨左側外壁填土高度h0的增加，結構橫斷面的彎矩曲線逐漸趨于中軸線對稱，結構各受拉區彎矩的極值絕對值逐步減小（支撐點除外，但其影響有限）；左側外壁根部彎矩方向的突變點和右側外壁中部正彎矩開始出現時對應的h0數值位于0.4～0.6h；故為保障結構板彎矩方向不發生大的變化，兩側壁板外側填土高差宜≤0.6h。

（5）本研究采用有限元分析方法，為內支撐式敞口隧道在雙側外壁非對稱填土荷載條件下的結構受力分布規律提供了重要參考，并為評估工況改變后原結構受力合理性提供了計算分析依據。

［1］陳廣深.敏感環境下明挖隧道設計方案研究［J］.西部交通科技，2020（4）：97-100.

［2］寧" 睿，李" 科，張世年，等.紅黏土接觸帶不同施工臺階高度對隧道結構的影響研究［J］.西部交通科技，2020（12）：109-112.

［3］馬" 亢，徐" 進，王蘭生.虛擬支撐力法數值模擬技術的應用［J］.西部交通科技，2007（2）：43-47.

［4］王一鳴，王浩璇．市政隧道框架箱涵結構設計研究［J］．赤峰學院學報（自然科學版），2019，35（6）：100-102.

［5］廖" 振，梁書亭，朱筱俊，等. 錯層板柱結構Push-over靜力彈塑性模擬分析［J］. 江蘇建筑，2023（6）：18-21.

［6］陳廣深.敏感環境下明挖隧道設計方案研究［J］.西部交通科技，2020（4）：97-100.

［7］鄒" 濤．城市隧道半敞開段結構受力分析［J］．城市道橋與防洪，2022（1）：217-220，25．

［8］陳衛軍. 半敞開地道結構頂板開洞優化分析［J］.現代隧道技術，2005（2）：32-36.

［9］代" 坤. 明挖地鐵車站空間計算模型與平面計算模型的對比分析［J］．隧道建設，2010，30（S1）：254-258.

20240320