基于Kriging模型的中承式系桿拱橋索力優(yōu)化研究

摘要：針對大跨度鋼管混凝土系桿拱橋吊桿索力優(yōu)化中有限元模型計算量較大的問題，文章以某大跨度鋼管混凝土系桿拱橋為例，提出了一種基于Kriging代理模型的系桿拱橋吊桿索力優(yōu)化方法。該方法基于有限元模型生成結構隨機變量與體系應變能的樣本數據，通過Kriging模型進行插值擬合，引入動態(tài)交叉、變異改進的遺傳算法對考慮結構體系應變能最小的吊桿索力優(yōu)化模型進行求解。結果表明：Kriging插值算法可以作為代理模型替代有限元模型進行吊桿索力優(yōu)化計算；動態(tài)遺傳算法相較于標準遺傳算法對吊桿索力優(yōu)化問題的收斂性更好；優(yōu)化后吊桿索力與優(yōu)化前大致相同，主梁彎矩最大降幅約為8%，軸力最大降幅約為13%，跨中撓度降幅約為13%。

關鍵詞：系桿拱橋；吊桿；索力優(yōu)化；Kriging插值；遺傳算法

中圖分類號：U448.22+5" " " " "文獻標識碼：A" " " "DOI：10.13282/j.cnki.wccst.2024.11.047

文章編號：1673-4874（2024）11-0158-05

0引言

系桿拱橋是一種以主梁、拱肋為基本結構構件的組合式拱橋橋型，由主梁和拱肋共同承受荷載，可以充分利用主梁的抗彎能力與拱肋的抗壓能力，同時系桿拱橋造型優(yōu)美，線型流暢，因此被廣泛應用于城市橋梁建設之中。系桿拱橋中連接拱肋和主梁的構件是吊桿，吊桿索力的大小直接決定了主梁上的內力分布趨勢，如何優(yōu)化吊桿索力一直是設計者和專家關注的重點問題。近年來，各專家學者對于系桿拱橋的吊桿索力優(yōu)化提出了不同的優(yōu)化設計方法。王憲玉等［1］針對大跨度鋼管混凝土系桿拱橋的索力優(yōu)化問題，采用能量法建立了不同約束條件下的吊桿索力優(yōu)化模型，采用有限元軟件進行分析，實現了吊桿設計階段的索力優(yōu)化與成橋階段的內力計算，相關結果為橋梁運營階段的吊桿索力測試提供了一定的依據。徐海賓等［2］以桁式鋼管混凝土系桿拱橋為工程背景，以系桿拱橋成橋合理拱軸線和結構體系應變能為目標函數，建立了系桿拱橋多目標索力優(yōu)化模型，通過分析拱橋上、下弦桿和主梁的內力結果，驗證了該優(yōu)化模型的有效性。潘建龍［3］以石浦大橋為研究對象，為確保橋梁結構運營階段的安全可靠，通過理論計算和有限元模擬的方法探討了系桿拱橋一次性索力優(yōu)化調試方法，并根據索力調整的實測結果驗證了該方法的可行性。丁祥文［4］為確定系桿拱橋索力的高效計算方法，基于數值迭代理論將系桿拱橋索力優(yōu)化的非線性問題轉化為線性問題，提出了基于單一控制指標的系桿拱橋索力優(yōu)化方法，并以不同張拉方案和迭代次數下的系桿拱橋安全儲備為基本指標確定了最優(yōu)的吊桿索力張拉方案，相關結果表明該方法可以良好地適用于實際工程。于孟生等［5］對影響矩陣法進行了改進，建立了一種基于改進影響矩陣的大跨度鋼管混凝土拱橋吊桿索力優(yōu)化模型，根據有限元計算結果和工程實測結果驗證了該方法的可行性。

從相關研究可以看出，目前大跨度鋼管混凝土系桿拱橋索力優(yōu)化問題的求解仍依賴于有限元模型的大量迭代計算，求解問題中仍存在計算效率不高、計算資源成本較大的問題。針對該問題本文提出了一種基于Kriging插值算法代理模型的系桿拱橋吊桿索力優(yōu)化方法，通過動態(tài)遺傳算法與Kriging模型對系桿拱橋索力進行了優(yōu)化求解，避免了有限元模型計算量較大的問題，相關結果可為類似工程提供一定的參考。

1工程概況

某中承式系桿拱橋跨徑布置為（100+450+100）m，其中主跨計算跨徑為450 m。主橋采用雙肢拱中承式鋼箱，橋面豎曲線半徑R=4 500 m，橋面寬45.8 m。邊跨拱肋與中跨拱肋處于同一平面，兩片拱肋之間通過K形風撐相連，邊跨加勁梁分別在中跨和邊跨的拱肋交匯處與拱肋固結。吊桿采用對稱式雙索面設計，單側吊桿共計38根，均勻分布于拱肋與系梁之間。橋型布置圖如圖1所示。

采用有限元軟件建立橋梁的數值計算模型，拱肋采用梁單元和殼單元共同模擬，系梁、立柱、橫梁、橫撐和風撐等結構構件采用梁單元模擬，吊桿和水平拉索由于僅受軸向力，故采用桁架單元進行模擬。橋梁主墩與拱肋、系梁之間采用全位移轉角固結約束，邊墩與上部結構之間的支座采用彈簧單元進行模擬，主、邊墩底部均設有彈簧單元支座。主梁兩端壓重采用質量單元進行模擬。有限元模型如圖2所示。

2索力優(yōu)化模型的建立

系桿拱橋是一種外部靜定、內部超靜定的橋型結構，主梁系桿主要承受壓力和彎矩，拱肋也同時承受軸向壓力和彎矩，而吊桿主要承受軸向拉力，將主梁上的荷載傳遞至鋼拱肋，為主梁提供豎向分力以確保主梁維持合理線形。對于系桿拱橋而言，結構體系主要承受拉壓應變能和彎曲應變能見式（1）：

U=∫Ma（x）22EaIadx+∫Na（x）22EaAadx+∫Mt（x）22EtItdx+∫Nt（x）22EtAtdx（1）

式中：U——結構應變能；

Ma、Na——荷載作用下拱肋的彎矩和軸力；

Mt、Nt——荷載作用下系桿的彎矩和軸力；

Ea——拱肋截面的彈性模量；

Et——系桿截面的彈性模量；

Ia——拱肋截面的抗彎慣性矩；

It——系桿截面的抗彎慣性矩；

Aa——拱肋截面面積；

At——系桿截面面積。

為計算系桿拱橋結構應變能，需要將結構進行單元離散化分析，假定離散后的單元截面積和彈性模量等屬性與整體單元一致，而彎矩沿單元方向呈線性變化，則任意離散單元的彎矩如式（2）所示：

M（x）=Ml，n+Mr，n-Ml，nLn（2）

式中：Ml，n、Mr，n——離散后微分單元左、右端的彎矩值；

[KG18mm]Ln——離散微分單元的單元長度；

n——離散單元數量。

同理，離散單元的軸力可表示為式（3）：

N（x）=Nl，n+Nr，n-Nl，nLn（3）

式中：Nl，n、Nr，n——離散后微分單元左、右端的軸力值。

此時，單元離散化后的結構體系應變能可表示為式（4）：

U=∑jn=1Ln6EnIn（M2l，n+Mr，nMl，n+M2r，n）+∑jn=1Ln6EnAn（N2l，n+Nr，nNl，n+N2r，n）（4）

式中：En、In和An——第n個離散單元的彈性模量、截面慣性矩和截面面積。

除結構彎曲應變能外，系桿拱橋系梁線形是結構的重要控制指標之一，為確保結構成橋后系梁撓度滿足要求，以吊桿與系梁連接位置作為系梁撓度控制點，則成橋后的系梁累積撓度可表示為式（5）：

δ=∑si=1δi（5）

式中：δ——系梁累積撓度；

δi——系梁各撓度控制點撓度；

[KG7.5mm]s——總撓度控制點數量。

由于系桿拱橋結構呈中心對稱，故進行優(yōu)化索力求解時僅需計算單索面一側索力值大小，令吊桿索力矩陣為X=（x1，x2，…，x19）T，為保證優(yōu)化后吊桿的可靠性，定義吊桿索力安全系數對決策變量取值范圍進行約束，如式（6）所示：

X*≤βX（6）

式中：X*——優(yōu)化后的索力矩陣；

β——安全系數。

根據上述分析，建立系桿拱橋索力優(yōu)化數學模型，如式（7）所示：

Find Xmin（U，δ）

s.t.X*≤βXδ≤δmax（7）

3基于Kriging模型的索力優(yōu)化流程

3.1基于Kriging的系桿拱橋響應模型的建立

采用有限元模型進行索力優(yōu)化迭代計算時，需要消耗很大的計算資源，本文采用Kriging模型對結構響應數據進行擬合，通過Kriging代理模型提升吊桿索力優(yōu)化的計算效率，節(jié)約計算成本。Kriging模型是一種基于Kriging插值算法［6-7］，以無偏估計為基本原理的響應面預測模型，核心思想是根據響應空間中待預測值與其他已知響應點的關系進行預測。Kriging插值基本模型可描述為：

y（x）=∑ni=1βifi（x）+z（x）（8）

式中：y（x）——系桿拱橋結構響應預測值；

βi——基函數的權值；

fi（x）——列回歸函數組成的基函數；

z（x）——系統偏差。

Kriging回歸模型中的預測響應與實際結構響應之間的系統偏差z（x）服從均值為0，協方差如式（9）的分布：

cov［z（u），z（v）］=σ2R（θ，u，v）（9）

R（θ，u，v）=∏mk=1Rk（θk，dk）=uki-vki（10）

式中：σ——系統偏差隨機分布的方差；

R（θ，u，v）——空間相關性函數；

θ——空間相關性函數參數；

u，v——樣本點參量；

d——樣本點之間的歐氏距離。

根據Kriging模型的基本插值原理，構建系桿拱橋隨機變量與結構響應的預測模型，令系桿拱橋隨機變量為T，結構應變能響應為Y，定義r（x）=［R（t，t1），R（t，t2），…，R（t，tn）］T，β=（FTR-1F）FTR-1Y，此時系桿拱橋隨機變量組合t下對應的預測彎曲應變能響應y的均值和方差如式（11）、式（12）所示：

μy⌒（t）=fT（t）β+rT（t）R-1（Y-Fβ）（11）

s2y⌒（t）=σ2z（1-rT（t）R-1r（t）+hT（FTR-1F）-1h）（12）

式中：μy⌒（t）——系桿拱橋試驗點響應均值；

s2y⌒（t）——響應預測的方差。

從上述模型構建原理可以看出，基于Kriging的系桿拱橋結構響應代理模型的預測精度比較依賴于空間相關性函數R的選取，考慮到實際工程結構隨機變量與結構響應之間的數據樣本呈高度非線性的特征，故本文選取高斯函數作為Kriging模型的空間相關性函數，高斯空間相關性函數表達式如式（13）所示：

R（θ，d）=exp-∑mk=1θk（uki-vkj）2（13）

式中：m——樣本點數量。

3.2基于改進遺傳算法的索力優(yōu)化模型求解

遺傳算法是一種以自然選擇和生物遺傳為基本仿生原理的智能優(yōu)化搜索算法，通過優(yōu)勝劣汰、適者生存的途徑將適應度較高的染色體進行保留和傳承，適應度較低的染色體淘汰。本文基于改進遺傳算法對系桿拱橋的索力優(yōu)化問題進行求解。

遺傳算法是一種收斂能力較強、收斂效率較高的全局尋優(yōu)算法，其收斂策略與偏好受算法中染色體交叉率Pc和變異率Pm的影響［8-10］，標準遺傳算法中交叉率Pc和變異率Pm的取值大多為常數，這就導致了算法在全局尋優(yōu)時收斂偏好較為單一，不能很好地適應具體的優(yōu)化問題。因此文本引入一種動態(tài)交叉、變異機制對標準遺傳算法進行改進，動態(tài)交叉、變異算子表達式如式（14）、式（15）所示：

Pc=Pc1-（Pc1-Pc2）（f*-favg）fmin-favg，f*＜favgPc1，f*≥favg（14）

Pm=Pm1-（Pm1-Pm2）（fmin-f*）fmin-favg，f＜favgPm1，f≥favg（15）

式中：Pc、Pm——動態(tài)交叉算子、變異算子；

Pc1、Pc2、Pm1、Pm2——給定的交叉、變異概率值；

f*——交叉步驟中個體的較小適應度；

favg——交叉、變異操作中種群的平均適應度；

fmin——交叉、變異操作中種群的最小適應度。

基于改進遺傳算法和Kriging代理模型的系桿拱橋索力優(yōu)化流程如圖3所示。

步驟1：采用有限元軟件計算系桿拱橋在隨機變量下的結構應變能，生成系桿拱橋隨機變量與結構應變能之間的數據樣本，并進行數據預處理。

步驟2：基于Kriging模型擬合系桿拱橋結構響應面，直至Kriging模型滿足精度要求。

步驟3：采用二進制編碼將吊桿拱橋索力編譯為遺傳算法染色體攜帶的遺傳，基于遺傳算法對考慮結構應變能最小的吊桿索力進行尋優(yōu)，采用Kriging代理模型計算染色體適應度。

步驟4：采用動態(tài)交叉、變異算子更新遺傳算法參數，進行交叉、變異操作，生成新的子代染色體并重新根據Kriging代理模型計算適應度值。

步驟5：判斷動態(tài)遺傳算法是否滿足算法終止條件，若滿足則輸出最優(yōu)索力結果，不滿足則返回上一步。

4結果分析

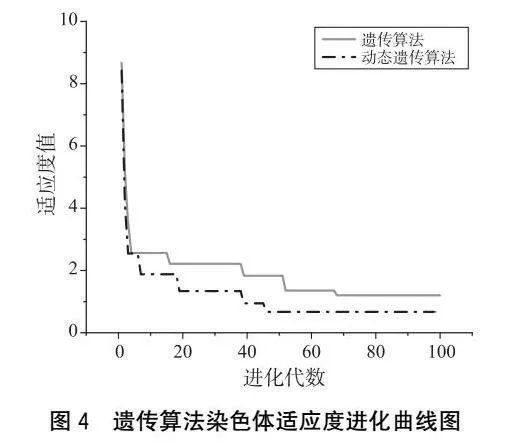
采用Matlab軟件中的Kriging工具箱對結構響應進行擬合，在Matlab中編寫動態(tài)遺傳算法程序調用Kriging模型工具箱進行系桿拱橋的索力優(yōu)化分析，為對比動態(tài)交叉、變異算子對索力優(yōu)化問題的影響，對相同樣本集采用標準遺傳算法進行優(yōu)化分析。圖4給出了標準遺傳算法和動態(tài)遺傳算法的染色體適應度進化曲線。從圖4可以看出，動態(tài)遺傳算法在迭代前期進化效率遠高于標準遺傳算法，且在進化后期動態(tài)遺傳算法仍保留了一定的變異能力，最終算法收斂精度遠高于標準遺傳算法。

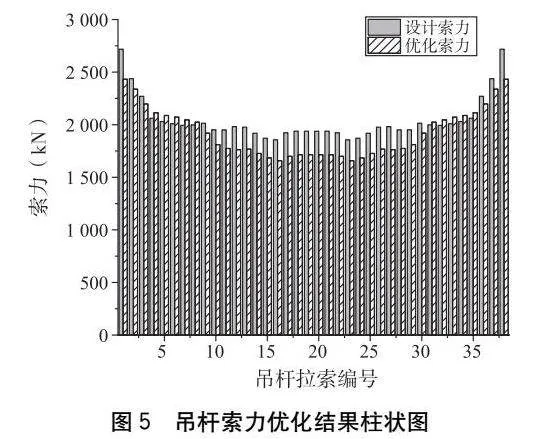
圖5給出了基于動態(tài)遺傳算法的索力優(yōu)化結果，由于結構對稱性，僅對1#～19#吊桿索力進行分析。觀察1#～19#吊桿索力可知，優(yōu)化前后索力從端點至跨中的增減趨勢大致相同，相較于設計索力1#～3#、9#～19#吊桿索力均有不同程度的降低，4#～8#索力存在小幅提升，各吊桿索力分布相較于優(yōu)化前均勻性更好。

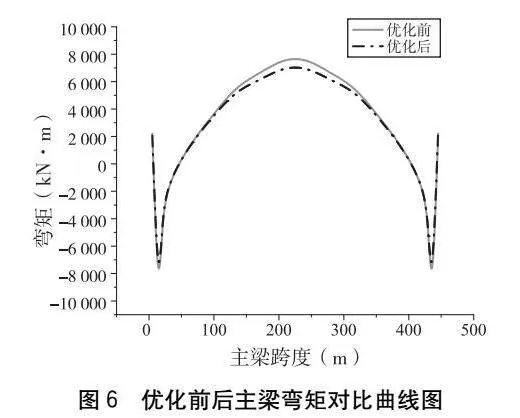
圖6為優(yōu)化前后的主梁彎矩對比曲線。從圖6可以看出優(yōu)化后主梁彎矩在拱腳附近與優(yōu)化前基本相同，跨中區(qū)域主梁彎矩存在一定的降低，跨中位置最大彎矩由7 687.72 kN·m降低至7 067.03 kN·m，降幅約8.07%。根據主梁上彎矩大小的變化可以得出，優(yōu)化后的索力在一定程度上降低了主梁的彎曲應變能，主梁彎矩分布相較于優(yōu)化前得到了一定的改善。

圖7為優(yōu)化前后的主梁軸力對比曲線。圖7的相關結果表明，優(yōu)化索力計算下的主梁軸力得到明顯降低，最大降幅出現在靠近跨中側，軸力值由-16 489.4 kN降低至-14 354.12 kN，降幅約13%，說明采用優(yōu)化索力后，主梁由軸力產生的拉、壓應變得到明顯減小。

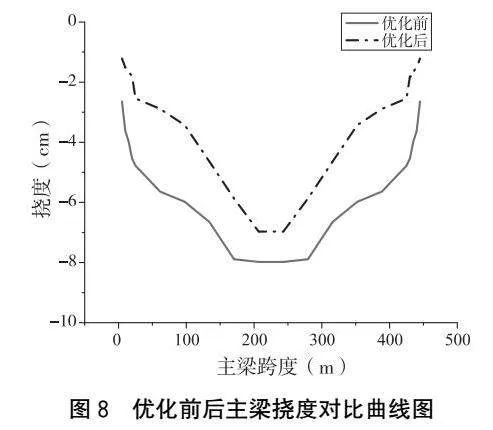
圖8為優(yōu)化前后的主梁撓度的對比曲線。由圖可知，優(yōu)化索力計算下的主梁撓度峰值由7.98 cm降低至6.97 cm，跨中撓度降幅約12.66%，說明主梁撓度控制目標函數明顯改善了優(yōu)化后的主梁撓度。

5結語

本文針對系桿拱橋索力優(yōu)化問題中存在的模型計算量大、優(yōu)化求解困難的問題，提出了一種基于Kriging代理模型的系桿拱橋索力優(yōu)化方法，使用Kriging作為結構代理模型替代有限元模型，采用動態(tài)改進的遺傳算法對吊桿索力進行尋優(yōu)求解，得到結論如下：

（1）采用Kriging模型可以避免有限元模型結構計算時計算量較大、計算資源耗費過多的局限性，Kriging模型在吊桿索力優(yōu)化中可以作為索力優(yōu)化代理模型進行迭代計算與分析。

（2）基于動態(tài)交叉、變異改進的遺傳算法在吊桿拱橋索力尋優(yōu)問題上的適應性相較于標準遺傳算法更好，種群進化效率更快，收斂精度更高。

（3）優(yōu)化后的吊桿索力相較于原索力較為均勻，除部分吊桿外，大部分吊索索力值存在不同程度的降低，主梁彎矩最大降幅約為8%，軸力最大降幅約為13%，跨中撓度降幅約為13%，結構應變能得到明顯改善。

參考文獻：

［1］王憲玉，王興武，梁孝，等.大跨度鋼管混凝土系桿拱橋吊桿索力分析［J］.振動與沖擊，2023，42（17）：306-313.

［2］徐海賓，雷余鵬，李磊.桁式鋼管混凝土系桿拱橋拱軸線及吊桿索力優(yōu)化［J］.科學技術與工程，2023，23（22）：9 659-9 665.

［3］潘建龍.石浦大橋鋼管混凝土系桿拱吊桿索力調整方法研究［J］.中國水運，2023（7）：136-138.

［4］丁祥文.剛性系桿拱橋吊桿張拉力迭代計算方法與張拉方案對比研究［J］.上海公路，2023（2）：62-67，86，189.

［5］于孟生，姚鑫玉，鄭皆連，等.大跨度鋼管混凝土拱橋吊桿索力優(yōu)化實用方法［J］.桂林理工大學學報，2023，43（1）：78-82.

［6］文啟軍，李杰，吳欣，等.基于優(yōu)化Kriging模型的小概率失效結構可靠度計算方法［J］.公路工程，2023，48（4）：37-43，90.

［7］侯賡舜，徐永利，徐志剛，等.基于Kriging算法與PSO算法的桁架機器人橫梁模塊智能優(yōu)化設計方法［J］.科學技術與工程，2023，23（18）：7 758-7 763.

［8］牟星辰，孟祥忠.基于改進遺傳算法的配電網多目標無功優(yōu)化設計［J］.青島科技大學學報（自然科學版），2023，44（6）：95-101，118.

［9］鄭堃，練志偉，顧新艷，等.采用改進兩點交叉算子的改進自適應遺傳算法求解不相關并行機混合流水車間調度問題［J］.中國機械工程，2023，34（14）：1 647-1 658，1 671.

［10］趙霖，王愛民，王崑聲，等.基于改進遺傳算法的虛擬制造單元繼承性重構調度技術［J］.紅外與激光工程，2022，51（11）：343-352.

作者簡介：鄧俊華（1992—），工程師，主要從事公路橋梁工程項目施工管理工作。

收稿日期：2024-05-08