預應力對剛構橋長期下撓的參數敏感性分析

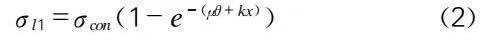
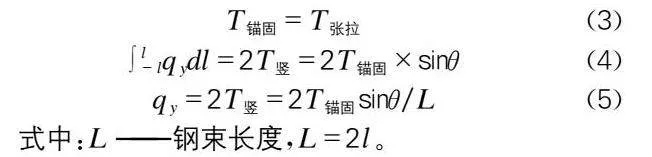
摘要：為探究預應力張拉時混凝土齡期、預應力管道摩擦系數μ和局部偏差系數k、預應力損失及底板預應力徑向力對大跨徑剛構橋成橋運營階段下撓的影響，文章依托某三跨連續剛構橋，采用Midas Civil軟件建立大橋空間仿真模型，以主梁十年運營階段下撓值為指標，分析其對預應力各項參數的敏感性。結果表明：隨著混凝土初次加載齡期的增大，主梁邊跨下撓值雖略有增加，但跨中下撓值減小明顯；隨著μ值或k值的增大，結構成橋階段有效預應力減小，均將導致結構下撓值增大，且對中跨跨中的下撓值而言，其對μ值或k值的變化最為敏感；頂板預應力及底板邊跨預應力損失對跨中下撓影響較小，相較于前兩者，中跨底板束預應力損失對跨中下撓值影響顯著；底板束徑向力消除對邊跨下撓影響較小，但對中跨下撓有顯著改善，其最大變化幅度已達到了233%，在設計時應予以考慮。

關鍵詞：連續剛構橋；混凝土齡期；預應力損失；徑向力；下撓值

中圖分類號：U448.23" " 文獻標識碼：A" " "DOI：10.13282/j.cnki.wccst.2024.11.030

文章編號：1673-4874（2024）11-0098-04

0引言

預應力混凝土連續剛構橋因其跨越能力良好、結構剛度大、建設周期短、造價低、行車舒適性高、后期運營維護費用少等優點，在連通河流、溝谷地形的橋梁方案比選中占有較大優勢。從現有實踐來看，早期修建的大跨徑連續剛構橋在長時間運營使用后，普遍出現跨中下撓過大，影響正常使用的現象。該問題不僅影響行車舒適性，過大撓度更會危及結構的安全。

針對剛構橋運營階段過大下撓的問題，已有部分學者展開了研究，并取得了一定成果。張瑞斌［1］針對跨中底板束對結構產生的“力”進行了有限元分析，研究表明此“力”的影響因素有底板束的布置角度及剛構橋的計算跨徑，在橋梁設計中需考慮該力對結構撓度的影響。黃金梅［2］以三跨連續剛構橋為工程實例展開了數值模擬分析，認為剛構橋下撓與環境相對濕度、混凝土剛度和自重有關。孫中洋等［3］基于實橋檢測結果研究了粉煤灰摻量等對結構撓度的影響，研究表明結構撓度對粉煤灰摻量敏感，應根據現場實際采集數據對結構的計算結果進行修正。張靜靜等［4］分析了自重變化以及梁體開裂對剛構橋下撓的影響，得出橋梁長期下撓與上述因素呈正相關，且橋面鋪裝超重對結構長期撓度影響最大，施工中應注意。

綜上所述，雖然上述學者從各個角度對剛構橋下撓的原因進行了分析，但系統全面針對預應力對結構下撓的影響卻鮮有研究。目前多數剛構橋實際下撓量遠超出預測值，已成為亟需解決的問題。鑒于此，本文以某主跨為180 m的連續剛構橋為例，利用Midas Civil軟件建立大橋仿真分析模型，研究預應力張拉時混凝土齡期、預應力管道摩擦系數μ和局部偏差系數k、預應力損失及底板預應力徑向力對剛構橋下撓的影響，以期得到不同參數對結構的敏感性。

1工程概況

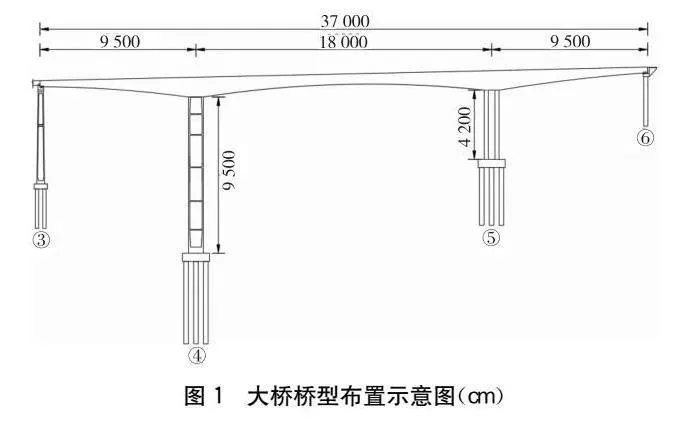
某橋上部結構采用三向預應力單箱單室變截面，跨徑組成為95 m+180 m+95 m。箱梁頂板寬12.6 m，底板寬7.1 m，梁高從跨中3.5 m以1.7次拋物線變化至箱梁根部11.5 m。箱梁底板厚度從根部截面的1.3 m按1.7次拋物線漸變至跨中及邊跨支點截面的0.32 m。該橋劃分為23個（9×3 m和14×4 m）掛籃懸臂澆筑節段，邊、中跨合龍段均為2 m，邊跨現澆段長3.8 m。大橋下部結構4#墩采用空心薄壁箱形截面，墩高95 m，5號墩采用雙肢薄壁墩，墩高42 m。該橋橋型布置如圖1所示。

2有限元計算模型

2.1幾何模型的建立

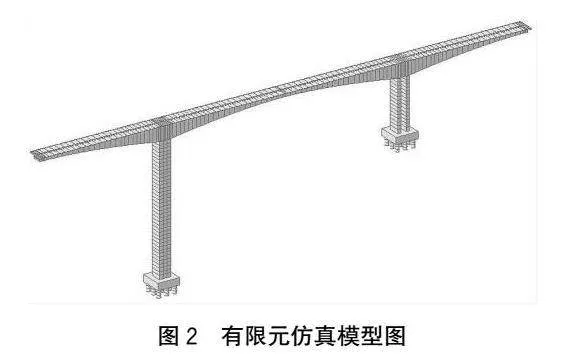
采用Midas Civil軟件建立大橋有限元模型，主梁根據設計及施工順序劃分并采用變截面梁單元模擬，下部結構共劃分124個單元。樁基底部采用固結，主梁邊跨采用彈性連接模擬支座，主墩與主梁之間采用剛性連接。全橋結構離散共計295個節點、252個單元。大橋有限元模型如圖2所示。

2.2模型參數取值

模型主要計算參數如表1所示。

3預應力參數敏感性分析

3.1預應力張拉時混凝土齡期對剛構橋下撓的影響分析

高墩預應力混凝土連續剛構橋通常采用掛籃懸臂澆筑，在懸臂施工各個節段中，需養護混凝土達到設計要求強度再張拉預應力鋼束。但在施工過程中，由于環境溫度、施工單位追求工期等原因導致混凝土往往未達到設計強度就進行預應力張拉，這將導致結構混凝土初次加載齡期縮短。加載齡期縮短將直接影響徐變系數的大小，而徐變系數關乎結構最終撓度。為此，本文選取3 d、5 d、7 d、9 d四個初次加載齡期，研究預應力張拉時混凝土齡期對結構下撓的影響。

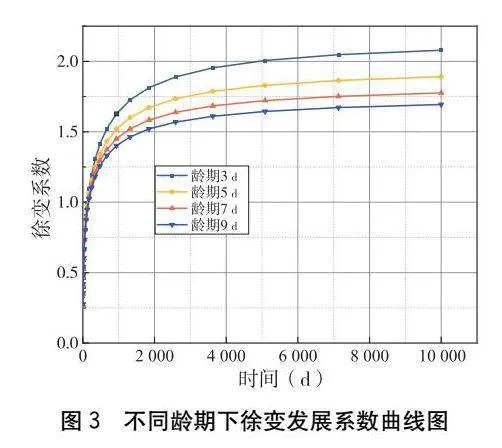
本文依據《公路鋼筋混凝土及預應力混凝土橋涵設計規范》（JTG3362-2018）中附錄C計算徐變系數，即收縮徐變模型采用JTG3362-2018模型［5］：

（t，t0）=0·βc（t，t0）（1）

式中：t0——加載時的混凝土齡期（d）；

t——計算時考慮時刻的混凝土齡期（d）；

（t，t0）——加載齡期為t0，計算考慮齡期為

t時的混凝土徐變系數；

0——名義徐變系數；

βc——加載后徐變隨時間發展的系數。

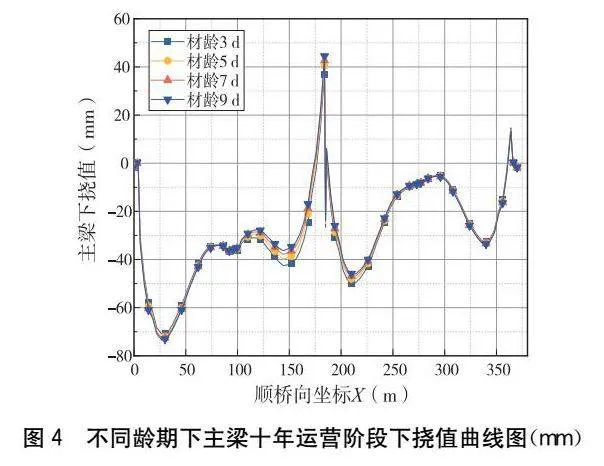
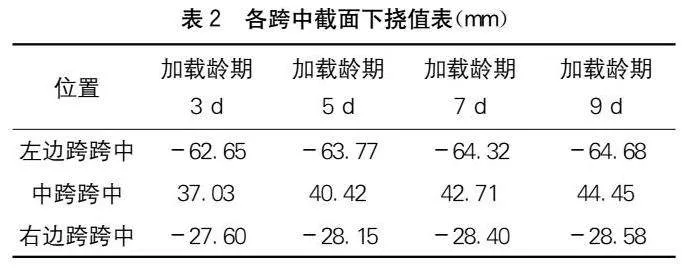
根據式（1）可計算出四種初始加載齡期的混凝土徐變系數，結果如圖3所示。將此徐變系數發展曲線輸入Midas Civil軟件可計算得到不同齡期預應力張拉時結構在成橋十年運營階段的主梁撓度，結果如圖4和表2所示。

由圖4和表2可得，混凝土齡期從3 d增加到9 d時，左、右邊跨下撓值分別增大了2.03 mm和0.98 mm，分別為加載齡期3 d的3.24%和3.55%；當加載齡期從3 d依次增至5 d、7 d、9 d時，中跨跨中下撓值分別增加了3.39 mm、5.68 mm和7.42 mm，增大百分比為9.15%、15.33%和20.03%。可見，隨著混凝土初次加載齡期的增大，主梁邊跨下撓值雖略有增加，但跨中下撓值減小明顯。

3.2摩擦系數u[HTHB]和偏差系數k[HTHB]對剛構橋下撓的影響分析

對于實際施工而言，預應力管道摩擦也會間接引起部分預應力損失，對于管道摩擦作用應不可回避。預應力與管道摩擦引起的預應力損失可通過式（2）計算：

σl1=σcon（1-e-（μθ+kx））（2）

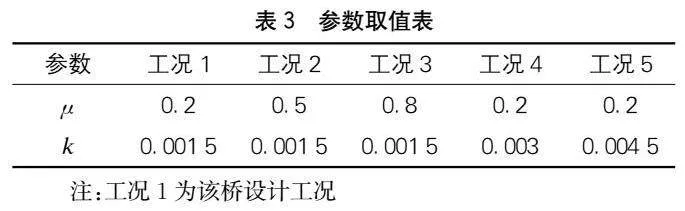
從式（2）可以看出，μ值、k值的變化將改變結構中的有效預應力，這勢必影響結構成橋線形。為此，本文采用單一控制變量法研究摩擦系數μ與偏差系數k對結構撓度的影響，計算參數取值如下頁表3所示。

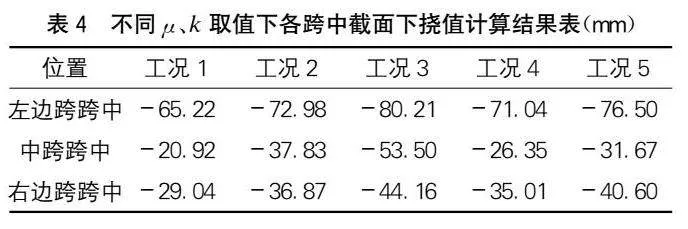
在不同摩擦系數μ和偏差系數k取值下，大橋在運營十年階段主梁跨中下撓值如表4所示。

由表4可知，隨著μ或k值的增大，結構成橋階段有效預應力減小，均將導致結構下撓值增大。對比工況1，隨著μ值增大，工況2和工況3跨中下撓值分別增大16.91 mm和32.58 mm，增幅分別為80.83%與255.73%；右邊跨跨中下撓值分別增大7.83 mm、15.12 mm，增幅分別為26.96%和52.06%。對比工況1，隨著k值的增大，工況4和工況5跨中下撓值分別增加5.43 mm、10.75 mm，增幅分別為25.95%、51.38%；右邊跨跨中下撓值分別增大5.97 mm、11.56 mm，增幅分別為20.55%與39.80%。可見，對于中跨跨中而言，下撓值對μ、k值的變化更為敏感。

3.3預應力損失對剛構橋下撓的影響分析

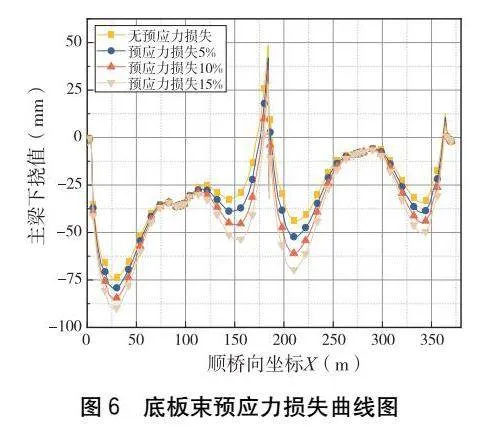
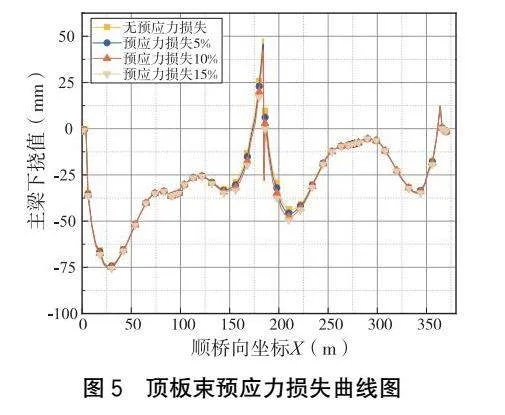
橋梁懸臂施工中，預應力張拉往往通過雙控，即既控制伸長量，又控制張拉應力。但大跨徑連續剛構橋施工是一個漫長的過程，在施工過程中可能出現張拉油壓表未及時標定、現場伸長量測量存在誤差等因素，導致預應力未到達設計值的情況。為分析其對剛構橋下撓的影響，本文選取頂板預應力束及底板預應力束預應力各損失5%、10%、15%來進行探討。其中，預應力損失通過改變鋼束的張拉應力實現，則結構運營十年階段主梁下撓計算結果如表5、圖5和圖6所示。

由表5、圖5和圖6分析可知：

（1）頂板預應力束損失對邊、中跨運營十年階段下撓值影響很小，當其預應力損失為15%時，邊、中跨下撓值最大變化幅度僅為3.4%。

（2）邊跨底板束距邊跨跨中較遠，對其下撓值影響較小。以右邊跨為例，當預應力損失為15%時，跨中下撓值變化幅度僅為2.1%。中跨底板束預應力直接作用于中跨底板，相較于邊跨底板束，其預應力損失對跨中下撓值影響顯著。當其預應力損失從5%增加至15%時，跨中下撓值分別增加3.53 mm、7.15 mm、10.74 mm，增加幅度分別為16.8%、34.1%與51.3%。

3.4跨中底板預應力徑向力對剛構橋下撓的影響分析

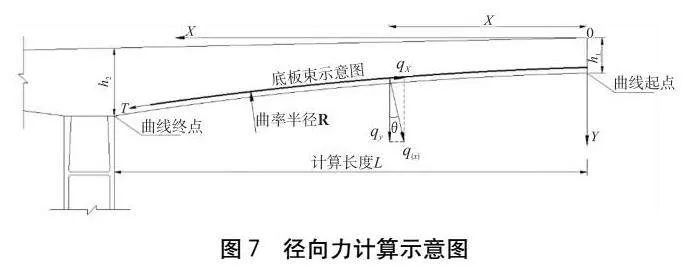
跨中底板預應力束的布置往往與箱梁底緣變化曲線一致呈上凸形狀，因此在預應力張拉后勢必在梁體中產生向下的徑向力，這將影響成橋階段跨中下撓值［6-7］。目前工程中常用有限元軟件并不能考慮此力的影響，因此徑向力對下撓值的影響應先計算其力的大小再施加至原模型進行分析。本文徑向力的計算采用以下簡化計算法，如圖7所示。

由于底板預應力鋼束采用對稱布置，在忽略鋼束兩端錨固點的彎起時，各鋼束力T的水平分力平衡，而鋼束豎直方向上的分力則由徑向力的分力qy與之平衡，由此可得到：

T錨固=T張拉（3）

∫l-lqydl=2T豎=2T錨固×sinθ（4）

qy=2T豎=2T錨固sinθ/L（5）

式中：L——鋼束長度，L=2l。

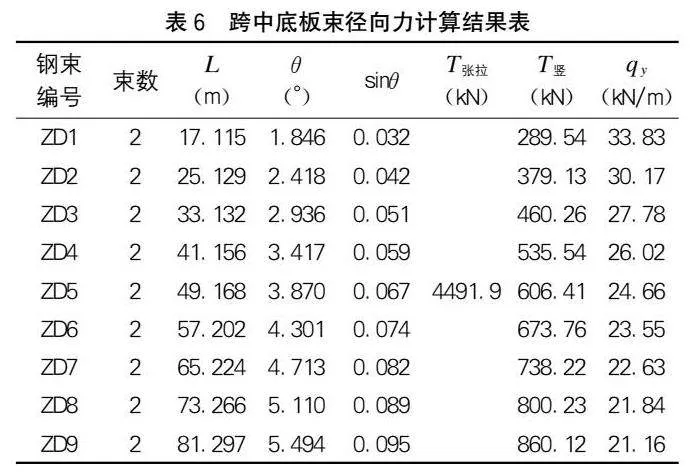
該橋的梁高變化方程為y=8×X1.7/84.51.7+3.5（m），θ=arctan（y′）。本橋中跨底板束采用j15.2-23型號的低松弛預應力鋼絞線，張拉應力為1 395 MPa，T張拉=4 491.9 kN，跨中各底板束徑向力計算結果如表6所示。

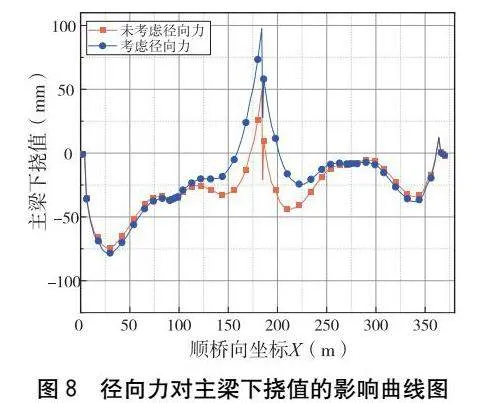
由圖8可知，徑向力消除之后中跨下撓得到顯著改善，而邊跨下撓變化不大。左、右邊跨在消除徑向力影響后，跨中下撓值分別從65.22 mm增加至70.00 mm、從29.04 mm增加至33.16 mm，變化幅度分別為7.3%與14.1%。中跨從墩中心線開始，消除徑向力后下撓值不斷減小，到跨中達到最大幅度，從未考慮徑向力的-20.92 mm遞增至27.83 mm，變化幅度為233%。可見跨中底板束產生的徑向力對結構下撓值影響顯著，在大跨徑剛構橋設計過程中不容忽視。

4結語

本文以某跨徑為95 m+180 m+95 m的連續剛構橋為工程案例，利用Midas Civil軟件建立大橋仿真分析模型，系統研究了預應力張拉時混凝土齡期、預應力管道摩擦系數μ和局部偏差系數k、預應力損失及底板預應力徑向力對剛構橋下撓的影響，得出主要結論如下：

（1）隨著混凝土初次加載齡期的增大，主梁邊跨下撓值略有增加，但整體變化不明顯，控制在3.55%以內；跨中下撓值改善較為顯著，最大變化幅度達到了20.03%。

（2）隨著管道摩擦系數μ或偏差系數k值的增大，結構成橋階段有效預應力減小，均將導致結構下撓值增大，且中跨跨中的下撓值對μ或k值的變化最為敏感。

（3）頂板預應力及底板邊跨預應力損失對跨中下撓影響較小，相較于前兩者，中跨底板束預應力損失對跨中下撓值影響顯著，最大幅度已達到了51.3%。

（4）底板束徑向力消除對邊跨下撓影響較小，但對中跨下撓有顯著改善，其最大變化幅度已達到了233%，設計時應予以考慮。

參考文獻：

［1］張瑞斌.連續剛構橋底板鋼束布置不同時的徑向力比較［J］.山東交通科技，2021（6）：60-63.

［2］黃金梅.大跨徑連續剛構橋長期下撓影響因素研究［J］.建筑機械，2023（5）：86-90，96.

［3］孫中洋，張顯明，李功文，等.基于監測研究的大跨徑連續剛構橋跨中下撓預測分析［J］.公路交通技術，2023，39（5）：120-128.

［4］張靜靜，饒春華.基于有限元模型的大跨度預應力混凝土連續剛構橋長期下撓因素分析［J］.交通世界，2023（22）：135-137.

［5］JTG 3362-2018，公路鋼筋混凝土及預應力混凝土橋涵設計規范［S］.

［6］車俊，武維宏，吳國松.基于水平底板索理念的大跨度PC連續剛構橋徐變下撓控制措施研究及工程應用［J］.工程建設與設計，2022（11）：109-112.

［7］燕卓.基于加中墩的大跨度連續剛構橋下撓處治研究［D］.昆明：昆明理工大學，2022.

作者簡介：劉耀文（1994—），工程師，主要從事路橋施工技術管理和經營管理工作。

收稿日期：2024-05-16