淺談計算機軟件Matlab在大學數學教學中的應用*

【摘" 要】 隨著信息技術的不斷進步，計算機輔助教學在數學學習中日益普及。鑒于Matlab軟件的強大功能，文章旨在闡述Matlab軟件如何在大學數學教學中有效地創設學習情境，并給出具體實例。將Matlab軟件與傳統教學方法相結合，可以顯著增強學生對知識點的理解和應用能力，從而提升數學學習效果。

【關鍵詞】 數學軟件；Matlab；大學數學

信息技術的飛速發展正深刻改變著教育領域，使得傳統的大學數學教育模式面臨前所未有的挑戰。在這一全新的教育生態中，計算機軟件的深度融合，不僅被看作是提升教學質量的關鍵路徑，還是促進學生深度理解數學概念、強化知識應用能力的重要手段。

一、數字化背景下數學教學改革的迫切性

當前，大學數學教學面臨諸多挑戰。其中，最為顯著的問題是教學方法和手段的相對單一。傳統的講授式教學導致學生缺乏實踐機會，實踐能力難以得到充分鍛煉。同時，大學數學課程本身具有較高的難度，作為基礎課程的課時安排又常常顯得緊張，難以滿足學生深入學習的需求。這些因素共同導致大學數學成為師生公認的“難教難學”科目，嚴重影響了學生的學習興趣和接受度。部分學生甚至對數學產生了畏懼心理。然而，數學作為理工科、管理類等眾多學科的基石，其重要性不言而喻。它不僅能夠鍛煉學生的邏輯思維與推理能力，而且這種思維方式在跨學科應用中同樣具有極高的價值。因此，探索更加動態、直觀的教學方法，以幫助學生更有效地跨越認知鴻溝，成為數學教學領域亟待解決的問題。通過將科技軟件與繪圖軟件相關知識點具象化，同時結合互聯網信息平臺進行信息檢索，以及學習數學在生產生活等領域中的案例，可以使學生更加深入、具體地理解相關知識的原理和應用價值，從而將數學融入生活。

二、計算機軟件與數學教學融合的重要性

隨著信息技術的日新月異，生產實踐中所面臨的復雜問題日益增多。這些問題往往需要綜合運用數學知識、數學建模技巧以及現代數學軟件才能得到有效解決。以計算機軟件為輔助教學工具的高等數學全新多媒體教學模式，在全球范圍內引起了廣泛的關注與探索。這一教學模式的興起，不僅順應了教育信息化的發展趨勢，也深刻改變了傳統高等數學教學的面貌，為學生提供了更加豐富、直觀、互動的學習體驗。例如，借助計算機軟件描繪出函數的動態圖像，直觀展現函數的變化軌跡與規律。這一過程不僅將抽象的數學概念轉化為直觀可感的圖像與圖形變換，還極大地豐富了教學手段，使原本顯得枯燥乏味的數學理論淺顯易懂，有效激發學生對數學學科的好奇心和探索欲，促進了他們更加積極主動地學習。

本文通過實例演示大學數學中極限、積分、線性代數等幾個典型例題的Matlab解法，旨在培養學生掌握計算機軟件在數學中的運用能力，以適應數字化背景下當前社會發展對應用型本科人才培養的要求。

三、Matlab在數學教學中的應用

Matlab，即矩陣實驗室（Matrix Laboratory），是美國MathWorks公司于1984年推出的一款數學軟件。其主要特點包括高效的數值計算和符號計算功能、完備的圖形處理功能、友好的用戶界面以及功能豐富的工具箱。Matlab作為一門高效的高級語言，在數學中有著廣泛的應用，主要用于數值計算、數據分析和可視化。由于數學課程具有較強的抽象性，因此教學中數學實驗的演示有助于學生對課程內容的理解。

（一）Matlab在函數極限中的運用

在Matlab中，用于計算極限的函數是limit，格式limit（f，x，a），其中f是需要求極限的函數表達式，x是函數中的變量，而a是變量x趨近的值。

例1，考察重要極限f（x）=的值。

解：只需輸入如下語言

gt;gt; syms x

limit（sin（x）/x，x，inf）

輸出結果為

ans=

0

gt;gt;x=-100：0.01：100；

y1=sin（x）./x；

figure，plot（x，y1）；grid on

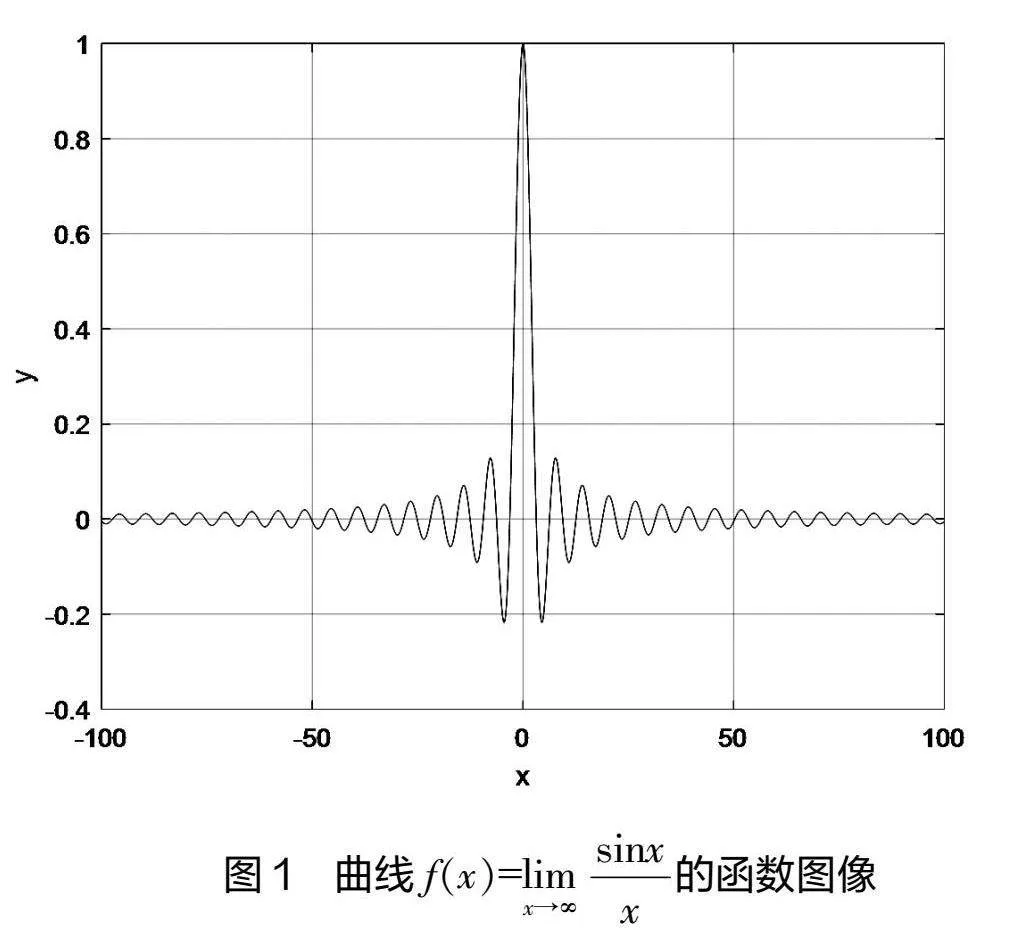
輸出圖形如圖1所示，從圖形中可以看出極限值為0。

根據圖象1顯示，當x→0時，函數值f（x）值無限逼近1；當x→∞時，函數值f（x）越來越逼近0。通過動態圖像或動畫，可以進一步展示函數隨參數變化而變化的過程，這對理解函數的動態性質和探索其潛在規律非常有幫助。這種方法不僅能夠幫助學生和教師更深入地理解函數極限的動態性質和復雜關系，還能夠激發學習者對數學的興趣，促進創新思維的發展。

例2，考察重要極限f（x）=（1+x）的值。

解：輸入如下輸入Matlab語句

gt;gt; syms x

limit（（1+x）^（1/x），x，0）

輸出結果如下

ans=

exp（1）

gt;gt; ezplot（'（1+x）^（1/x）'，［0，30，0，3］）

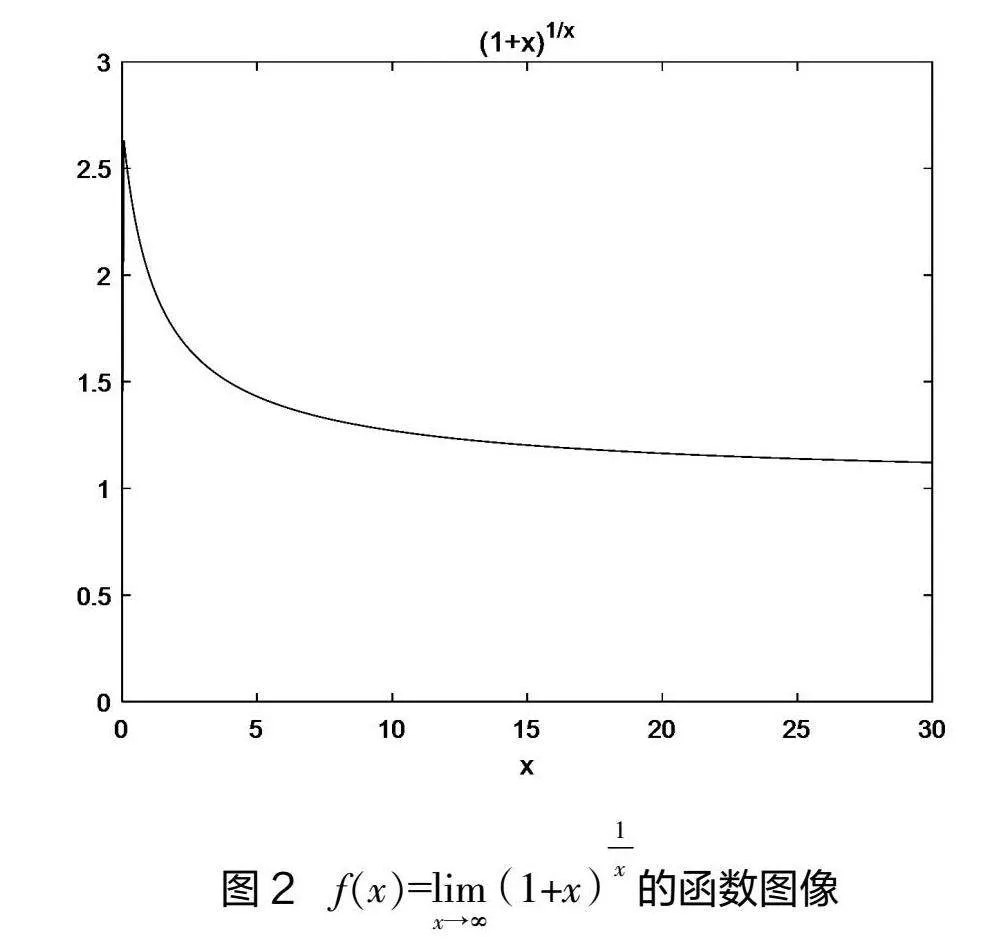
輸出圖形如圖2所示，從圖形中可以看出極限值為e。

結合圖像2可知，當x→0時，函數值f（x）值越來越接近e。

上述第二個極限，公式非常簡單，但是在傳統教學中，教師要在有限的課堂時間中推導過程，并把相關知識點傳授清楚，絕非易事。尤其單一的推導過程不僅難且枯燥，如果在教學過程中，通過簡單的推導證明，輔助利用Matlab的畫圖編程功能，可以一目了然。

（二）Matlab在積分中的運用

高等數學的概念大多是從日常生活的案例中抽象出來的，比如定積分的基本概念。首先展示曲邊梯形的面積，通過分割、近似、求和和取極限四個步驟得到。如果利用Matlab軟件編程，可以動態地演示不斷分割的過程，幫助學生更好地理解曲邊梯形的面積。

1. Matlab求解不定積分

在Matlab中，主要用函數integral來表示積分，簡寫int。不定積分的函數形式為int（f，x），其中，f（x）是積分函數，x是積分變量。要使用int函數，需要在Matlab中定義一個符號變量，這可以通過syms命令完成。然后，可以使用int函數來對這個符號變量所代表的表達式進行積分。

例3，利用Matlab求y=x^4+2x+3的不定積分.

解：要求解y=x^4+2x+3的不定積分，只需輸入如下輸入Matlab語句：

syms x

y=x^4+2*x+3

int（y，x）

輸出的結果是：

ans=

（x*（x^4+5*x+15））/5.

也就是說，這個函數的不定積分是（x*（x^4+5*x+15））/5。但是在Matlab中，不會出現常數C，因此需要手動加入C。因為在符號計算中，int函數主要關注的是被積函數與積分變量之間的關系，以及這些關系如何導致積分表達式的變化，而不是積分的具體值（除了定積分外）。

2. Matlab求解定積分

求解定積分與不定積分類似，只需要在integral函數中指定積分上下限即可。在Matlab函數中，定積分的通用形式是integral（f，x，a，b），簡寫為int（f，x，a，b）。其中，f（x）是積分函數，x是積分變量，a是積分上限，b是積分下限。

例4，利用Matlab計算y=sin4xdx.

解：要求解y=sin4xdx的定積分，只需輸入如下輸入Matlab語句：

syms x；

f=int（sin（x）^4，0，1）

執行命令，輸出的結果是：

f=sin（4）/32-sin（2）/4+3/8.

由此可見，使用Matlab來求解比較復雜的積分，更簡潔，節省了手工計算量。

（三）Matlab在線性代數中的運用

利用Matlab強大的運算功能，可以解決線性代數中復雜的運算，如求行列式的值、矩陣的逆運算、矩陣的秩等。

行列式的值：在Matlab中，可以使用det函數來計算矩陣的行列式值。這個函數以一個矩陣作為輸入，并返回該矩陣的行列式值。

矩陣的逆運算：在Matlab中，求矩陣的逆運算可以使用inv函數。然而，并不是所有的矩陣都有逆矩陣，只有非奇異矩陣（即行列式不為零的矩陣）才有逆矩陣。

矩陣的秩：在Matlab中，求矩陣的秩可以使用rank函數。這個函數能夠返回矩陣的非零子式的最大階數，即矩陣的秩。

例5，對矩陣A=8 2 -1

4 4" 2

3 1 -1做如下運算：（1）求a=|A|；（2）求B=A-1；（3）求c=rank（A）.

解：輸入相應的Matlab程序為

A=［8 2 -1；4 4 2；3 1 -1］；

a=det（A）；

B=inv（A）；

c=rank（A）.

結果

a=-20，

B=0.3000" "-0.0500" -0.4000

-0.5000" 0.2500" "1.000

0.4000" "0.1000" "-1.2000，

c=3.

函數極限、微積分等基礎知識是高等數學中非常重要的內容，學會求解與使用至關重要。Matlab的求解計算功能，可以使計算過程縮短、簡潔。

四、結語

Matlab作為一款集數值計算、符號計算、可視化及編程功能于一體的軟件，在高等數學及其相關領域的教學與應用中展現出了巨大的價值。其強大的數據處理和圖形繪制能力，不僅讓“數形結合”這一教學思想得以深入實踐，還極大地提升了學生的學習興趣和效果，為大學數學課堂注入了新的活力。Matlab為數學學習帶來了極大的便利性。它不僅是一個計算工具，更是一個研究和學習的平臺。Matlab使得原本抽象和高深的數學理論變得形象化和可視化，有助于學生更好地理解和掌握數學知識。此外，Matlab也提高了學生解決實際問題的能力。通過使用Matlab，學生可以模擬和解決各種實際問題，從而培養他們解決實際問題的能力。

參考文獻：

［1］ 高艷超，成麗波，呂堂紅. 信息化背景下大學數學課程混合式教學模式研究［J］. 牡丹江教育學院學報，2022（07）：81-83.

［2］ 林小圍. Mathematica在大學數學課堂的應用［J］. 合肥師范學院學報，2018（36）：62-65.

［3］ 王海英. 數學知識、數學建模、現代數學軟件關系與結合途經的探討［J］. 中國地質教育，2011，20（01）：95-97.