基于組合賦權(quán)-TOPSIS模型的邊坡穩(wěn)定性預(yù)測研究

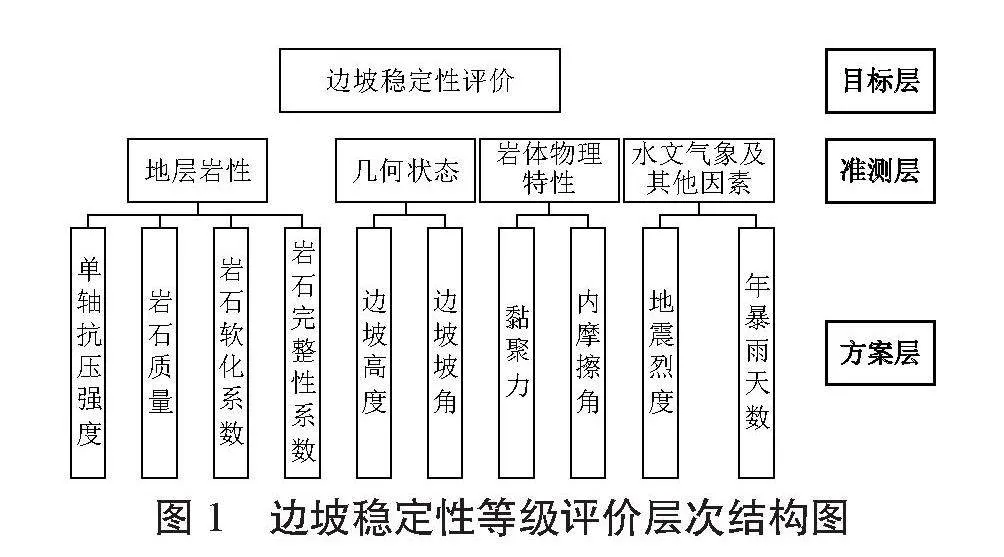
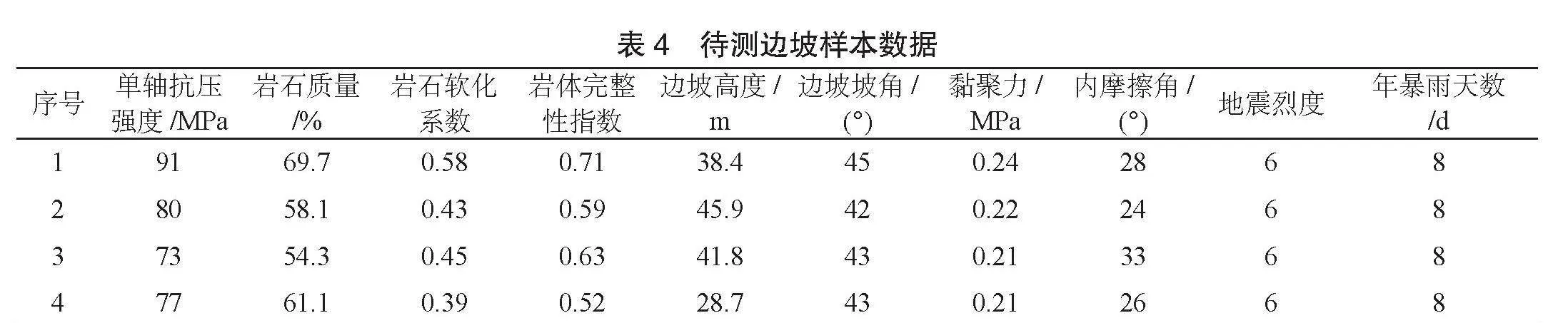
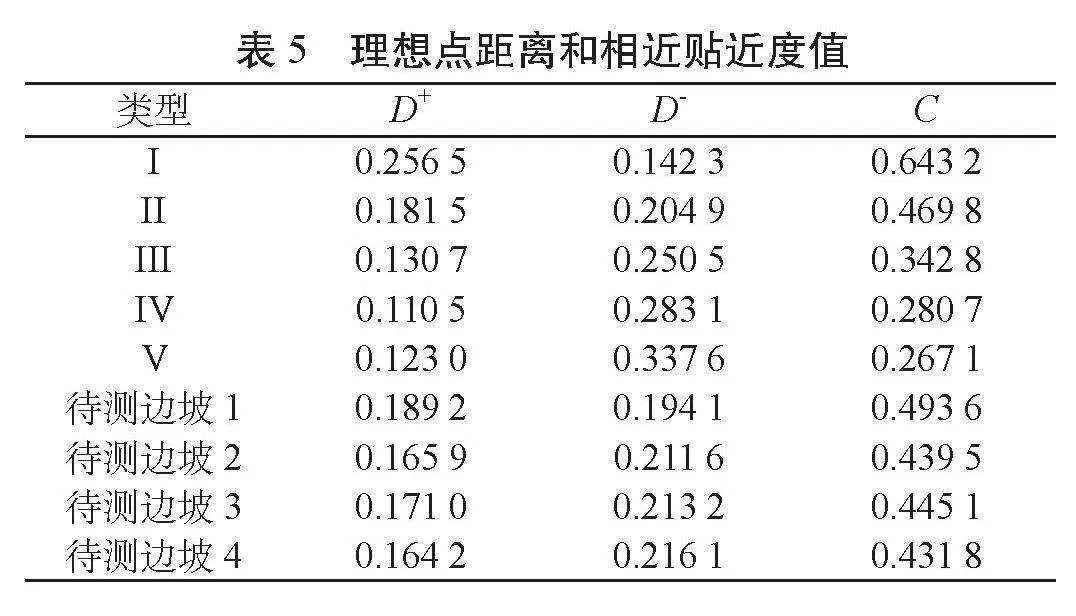
摘要 邊坡穩(wěn)定性評價的準(zhǔn)確性直接關(guān)系到工程建設(shè)的安全、經(jīng)濟(jì)性和環(huán)境影響。針對巖土工程中邊坡穩(wěn)定性評價的模糊性問題，該研究提出了一種基于博弈論組合賦權(quán)法與TOPSIS模型的新評估體系。采用了博弈論賦權(quán)法來確定影響邊坡穩(wěn)定性的關(guān)鍵因素權(quán)重，確保了權(quán)重分配的客觀性和合理性；再通過引入了TOPSIS模型，將定性指標(biāo)定量化，便于進(jìn)行比較和排序；選取了地層巖性、邊坡幾何形態(tài)、巖體物理特性、水文氣象等條件下的20個關(guān)鍵因素，并將該模型的預(yù)測結(jié)果與4組實際邊坡工程進(jìn)行對比。結(jié)果表明：該文預(yù)測結(jié)果與實際情況完全吻合，進(jìn)而驗證了所提方法的有效性，為邊坡穩(wěn)定性評價提供了一種新的思路。

關(guān)鍵詞 組合權(quán)重；邊坡穩(wěn)定性；TOPSIS；層次分析法；熵權(quán)法

中圖分類號 U416 文獻(xiàn)標(biāo)識碼 A 文章編號 2096-8949（2024）15-0007-03

0 引言

邊坡穩(wěn)定性評價在巖土工程中起著重要的作用，它直接關(guān)系到工程的安全和經(jīng)濟(jì)效益[1]。隨著城市化的快速發(fā)展，邊坡工程在基礎(chǔ)設(shè)施建設(shè)中的應(yīng)用變得日益廣泛，如高速公路、鐵路和水利工程等。這些工程常面臨復(fù)雜的地質(zhì)條件和環(huán)境挑戰(zhàn)，使得邊坡穩(wěn)定性評價的重要性日益凸顯。然而，邊坡穩(wěn)定性評價過程中存在的不確定性和模糊性，如數(shù)據(jù)的不完整性和不一致性，給評價工作帶來了許多困難[2-3]。傳統(tǒng)的評價方法，在處理多因素綜合評價和不確定性信息方面仍存在局限性。因此，該研究旨在探索一種結(jié)合主觀和客觀信息的組合賦權(quán)方法，并引入TOPSIS模型，以提高邊坡穩(wěn)定性評價的準(zhǔn)確性和可靠性。……