基于動態多種群機制的增強花授粉算法

摘 要：

針對花授粉算法易陷入局部最優、收斂精度不足和過早收斂的問題，提出一種基于動態多種群機制的增強花授粉算法（DMEFPA）。首先，DMEFPA使用一種融合個體適應度值和相對距離的方法挑選中心個體，使選出的個體既保持較高質量又保持在搜索空間的分布廣泛，再將剩余個體劃分到距離最近的中心個體構成多種群，隨后依據概率來考慮是否接受種群狀態變化。其次，各子群通過隨機順序動態構成環拓撲進行個體遷移，以增強種群多樣性避免陷入局部最優。最后，通過改進局部搜索策略，以完善對解空間的探索。選用CEC2017測試函數集中的12個函數作為性能基準函數，將DMEFPA和其他5個改進算法：SCFPA、HLFPA、WOFPA、AMSSA、SHSSA進行評測，并對改進策略進行了消融實驗。基于實驗結果的Friedman檢驗表明，在改進策略的共同作用下，DMEFPA能獲取最優的性能，且全局收斂性能較為穩定。

關鍵詞：花授粉算法； 多種群； 動態拓撲； 個體遷移； 局部搜索策略

中圖分類號：TP301.6"" 文獻標志碼：A""" 文章編號：1001-3695（2024）12-020-3671-08

doi： 10.19734/j.issn.1001-3695.2024.06.0151

Enhanced flower pollination algorithm by adopting dynamic multi-group mechanism

Li Dahai， Ling Jiyuan， Wang Zhendong

（School of Information Engineering， Jiangxi University of Science amp; Technology， Ganzhou Jiangxi 341000， China）

Abstract：

Aiming at overcoming drawbacks of lower accuracy and being trapped easily to local optimums of the flower pollination algorithm （FPA）， this paper proposed an enhanced flower pollination algorithm based on dynamic multi-subgroup mechanism （DMEFPA）. Firstly， DMEFPA selected the central individuals using a method that combined individual fitness values and relative distances， ensuring that the selected individuals maintain high quality while being widely distributed in the search space. Then， it assigned the remaining individuals to the closest central individuals to form multiple subpopulations， and considered the acceptance of population state changes based on probability. Secondly， each subpopulation dynamically formed a ring topology in a random order for individual migration to enhance population diversity and avoid local optima. Finally， the algorithm improved local search strategies to refine the exploration of the solution space. 12 functions from CEC2017 test suit were selected as the benchmark to evaluate the performance of DMEFPA and other 5 algorithms： SCFPA， HLFPA， WOFPA， AMSSA and SHSSA. Friedman test based on experimental results show that DMEFPA can achieve the supreme performance. Ablation experiments were also conducted to verify effectiveness of proposed improvement strategies. Experimental results illustrate that DMEFPA can achieve the outstanding performance and with stable convergence under the joint of all improvement strategies.

Key words：flower pollination algorithm; multi-groups; dynamic topology; individual migration; local search strategy

0 引言

花授粉算法（FPA）是由Yang［1］于2012年提出的一種高效智能優化算法。FPA的全局和局部搜索過程分別模仿植物的異花授粉和自花授粉過程，并平衡全局搜索和局部搜索之間的切換。由于FPA具有易于實現、參數少和魯棒性強等特點，其已經應用于求解諸多領域的復雜優化問題，如信號去噪優化問題［2］、任務調度優化問題［3］等。與其他智能優化算法類似，FPA在求解高維復雜優化問題時，存在易陷入局部最優和收斂精度低等缺陷［4～6］。目前，國內外學者已經提出了諸多的改進或者增強的FPA。

寧杰瓊等人［7］提出一種基于t-分布擾動策略和變異策略的花授粉算法（TMFPA）。TMFPA利用混沌映射初始化種群以解決種群初始分布不均勻的問題，且采用t-分布來擾動隨機個體加快算法的收斂速度。洪露等人［8］提出基于三重動態調整的花授粉算法（HLFPA）。HLFPA使用正弦函數來動態調節切換概率以平衡算法探索和開發，還在全局搜索過程當中引入動態因子，并在局部搜尋過程當中引入正余弦步長因子以增強算法跳出局部最優的能力。張水平等人［9］提出基于動態調整和協同搜索的花授粉算法（FPADC）。FPADC利用霍爾頓序列以某一質數作為基數對其進行切分來生成在解空間中不重復且均勻分布的初始種群，并對種群內個體進行分工以提升算法的收斂速度與精度。Wang等人［10］提出基于共生制度的蝴蝶和花授粉混合算法（MBFPA）。MBFPA在每次迭代過程中都將種群劃分為兩個子群并分別使用蝴蝶飛行方式和花授粉飛行方式，且為兩個子群引入基于共生機制協同進化方法。Tawhid等人［11］提出一種鯨魚和花授粉混合算法（WOFPA）。WOFPA采用WOA的螺旋模型和隨機搜尋方程代替FPA的全局搜索方程，以提升算法的尋優精度。Al-Betar等人［12］提出一種基于多種群機制的孤島花授算法（ISFPA）。ISFPA在迭代初期利用孤島模型將種群隨機劃分為多個子群，并為不同子群設立個體轉移策略，以增強種群的多樣性并提升算法的尋優能力。陳西成等人［13］提出應用小生境混沌搜索策略的改進花授粉算法（NCFPA）。NCFPA在每次種群更新過程中利用小生境策略圍繞適應度值高的個體生成小種群，并淘汰適應度值較差的個體以提升算法的全局優化能力，引入混沌序列對精英個體進行局部優化以增強算法的搜索精度。

上述對FPA的改進主要集中在以下三點：a）優化種群的初始分布，如TMFPA［7］及FPADC［9］分別利用混沌映射與霍爾頓序列初始化種群，使得初始種群均勻分布；b）保持或增強種群的多樣性，如TMFPA［7］利用t-分布擾動隨機個體以保持多樣性，ISFPA［12］將種群劃分為多種群并構建子群間信息交流以保持種群的多樣性；c）融合有效的全局或局部搜索機制，如NCFPA［13］利用小生境機制淘汰較差個體以提升算法的尋優能力，MBFPA［10］將種群劃分為兩個子群并引入共生機制以提升算法的探索和開發能力。為進一步提升FPA的性能，本文提出一種基于動態多子群機制的增強花授粉算法DMEFPA，并主要采用了以下三項改進策略：

a）提出一種融合個體適應度值和距離信息的方法將花粉種群劃分為多個子群，并依據概率來考慮是否接受種群多樣性變化。該策略使各子群盡量均勻地分布在解空間中以更有效地探索解空間。

b）將多子群通過隨機順序構成環拓撲結構，通過適應度排序來選擇合適的遷移個體，并將遷移個體替換為下一子群中適應度值最差的個體，加強子群間的信息交流以提升種群多樣性，降低算法陷入局部最優的概率。

c）利用改進局部搜索策略以更好地平衡種群的探索和開發能力，并增強算法的尋優能力。

本文采用了CEC2017中的12個測試函數將DMEFPA和其他5個改進算法，即HLFPA［8］、WOFPA［11］、SCFPA［14］、AMSSA［15］以及SHSSA［16］進行對比實驗，并對DMEFPA采用的改進策略進行了消融實驗。實驗結果表明，在綜合改進策略的共同作用下，DMEFPA的綜合優化性能突出，且全局收斂性能穩定。

1 花授粉算法

FPA是模擬自然界植物的自花授粉與異花授粉過程。授粉的傳播媒介有生物和非生物兩種。生物授粉通常視作異花授粉，可在大范圍內傳播。非生物授粉通常視作自花授粉，傳播媒介主要有風、雨等。為簡化問題，Yang在算法中假定每株植物僅開一朵花，每朵花僅產生一個花胚，一個花胚即優化問題的一個解。花授粉的過程可歸納為以下四點：

a）植物的異花授粉對應算法的全局尋優階段，生物載體攜帶花粉并執行Lévy飛行規律。

b）非生物的自花授粉對應算法的開發階段，局部搜索是同種類的植物不同花朵之間通過風實現傳粉。

c）繁衍概率對應花朵的恒常性，兩朵花（個體）的相似和關聯性成比例。

d）植物的生物授粉與非生物授粉的切換概率由參數p∈［0，1］決定。由于受到位置、風等因素影響，整個授粉過程中，局部授粉的概率更大。

由上述描述可知，異花授粉（全局授粉）和自花授粉（局部授粉）為FPA的核心。FPA的全局尋優公式描述如下：

Xt+1i=Xti+L（λ）（Xti-Xbest）" rand gt; p（1）

其中：Xti、Xt+1i分別表示的是種群中的第i個粒子的第t代解及其下一迭代解。Xbest是種群迭代過程當中的最優解，L（λ）為服從Lévy飛行的步長，其計算如式（2）所示。

L（λ）～λΓ（λ）sin（πλ/2）π·1s1+λ（sgt;gt;s0gt;0）（2）

其中：Γ（λ）是標準伽馬函數，λ通常設為1.5。利用式（1）進行全局尋優，在全局最優解Xbest的引導下，種群會容易獲得更優解，同時因為Lévy飛行每次迭代都能獲得一個隨機步長，以確保種群的多樣性。

FPA的局部尋優公式描述如下：

Xt+1i=Xti+ε（Xtj－Xtk）" rand≤p（3）

其中：Xtj和Xtk是花粉種群中隨機挑選的兩個不同個體；ε是［0，1］均勻分布的隨機數。其目的是用ε擾動確保每次獲取的解都具有隨機性。

2 基于動態多種群機制的增強花授粉算法

基于對式（1）的分析可知，原FPA在每輪迭代中都是基于貪婪策略引導種群中所有個體向著已知最優個體位置靠近。這意味花粉種群的多樣性會隨迭代次數的增加快速降低，從而導致算法易陷入局部最優、收斂精度低和早熟［17］。本文提出的DMEFPA采用多子群以及依概率選擇接受種群狀態變化，并使用基于動態環型拓撲的個體遷移機制來提升種群的多樣性，最后利用改進局部搜索策略增強算法局部尋優性能。

2.1 動態多子群策略

目前已有許多學者提出使用多種群方法來增強FPA的性能。多種群方法一般是將初始種群劃分為多個子群，并讓不同的子群探索解空間的不同區域。多種群劃分方法通常基于適應度信息、距離信息或隨機來劃分。隨機多種群的劃分方法［12］雖然有助于維持種群多樣性，但由于種群劃分完全隨機確定，在后續迭代中可能無法維持子種群的個體質量，易導致算法陷入隨機性過高和搜尋精度不高的窘境。基于適應度值［13，18］的多種群劃分方法通常依據個體適應度的優劣來劃分子種群。雖然該類種群劃分方法能夠幫助種群迅速收斂，但無法避免因個體聚集在局部最優附近所導致被劃分的子種群聚集的現象，從而使種群過分趨優而無法對解空間進行更充分的探索。因為基于距離的多種群劃分［9，19］ 完全忽略個體的適應值，所以該子種群劃分方法可能造成某些子群所含個體總體質量較低的問題。基于距離的多種群劃分有利于構成優勢子種群，因為屬于各個子種群的個體完全由個體位置確定，聚集在當前最優位置附近的個體可能被劃分到同一個子種群。基于上述分析，本文提出的DMEFPA使用了一種綜合考慮個體適應度值和個體間距離信息的子種群劃分方法，提高子種群個體總體質量，也同時維持子種群的多樣性，從而增強算法的尋優性能。

本文提出了動態多種群策略，該策略首先包括一種結合個體適應度和距離信息的多子種群劃分方法，以及依據種群離散度決定是否重新劃分種群的機制。假設以適應度值最小的解為當前最優解。該方法首先對種群中所有個體利用適應度值進行由小到大排序，設Si表示排序后個體的序號。隨后計算序號為Si的個體與前Si－1個花粉個體之間的歐氏距離的平均值Li，其公式為

Li=1Si－1∑Si－1m=1∑Dj=1（XSi， j－Xm， j）2（4）

為使適應度值最優個體引導子群，對適應度值最優個體S1賦予種群中的最大平均距離L1。分析式（4）可知，Li越大，表示該花粉個體與適應度值更優個體間的偏離程度越大。隨后對每個個體的平均距離Li進行由大到小的排序，并對所有排序后的個體賦排序編號Qi。再按式（5）為每個花粉個體賦予綜合權重Ei作為挑選子群中心個體的指標。即對所有花粉個體的權重Ei進行由小到大排序，并選擇排序靠前的n個花粉個體作為構建n個花粉子群的中心個體。式（5）為

Ei=Si+Qi（5）

按上述方法挑選子群中心的動機是：適應度值較小的個體序號Si也較小，擁有更大平均距離Li的個體的序號Qi越小。當個體同時擁有較小的適應度值及較高的平均距離時，其權重Ei也會越小，從而可以確保跳出的作為子種群中心的個體既具有較好的適應度，又保證被選出的個體較為分散。

在挑選出子群中心個體后，將種群中除被選出的中心個體之外的剩余個體劃分到距離其最近的中心個體所屬的子群。按上述方法挑選子群中心個體不僅考慮了適應度值，同時還考慮了個體與適應度值更優個體間的平均距離，可以使子群中心個體同時具有較優適應度和相對分散兩種特性，從而使以中心個體為核心來劃分的子群，既保證了子群的分布又具有相對分散的特性。上述的子群劃分機制依賴參數：子群數量n。子群數量過多會使每個子群擁有的個體數量過少并降低子群機制對算法的影響。文獻［17］指出，在多數情況下，子群數量為3時可以在降低分群復雜性的同時還能保證種群的多樣性，并使算法具備良好的收斂性能。本文也選擇將參數子群數量n的大小設為3。圖1（a）展示了只依據適應度挑選最優個體作為子群中心的多種群劃分效果圖。圖1（b）顯示了使用本文方法進行多種群劃分的效果圖。如圖1（a）所示，只依據個體適應度挑選出的子群中心個體彼此靠近，導致分群效果不佳。如圖1（b）所示，通過本文方法選出的子群中心在保證適應度較低的同時又相對分散，所以能夠將整個種群較為均勻地劃分為3個子群，有利于對解空間進行探索和開發。

為了避免因每輪迭代都劃分子群造成的計算復雜度增大的問題，本文提出的動態多種群策略還包括一種依據種群離散度來決定是否重新劃分種群的方法。該方法首先按式（6）計算其值介于［0，1］內的種群多樣性指標Div，并使用Div值計算作為重新劃分子群的概率P。即以概率P接受種群是否使用反向學習來重新生成種群并進行子群的劃分。

Div=ω1×1N∑Ni=1exp（－‖Xi－1N∑Ni=1Xi‖2）+ω2×exp（－tT）（6）

其中：N表示種群個體的數量；Xi為種群中第i個個體；t為當前迭代次數；T為最大迭代次數；ω1和ω2為調節種群離散度和迭代次數對于Div值的權重系數，此處設ω1為3/4并設ω2為1/4。Div同時考慮了種群的離散程度及算法的迭代次數，并為種群的離散程度賦予更高的權重。再按式（7）對Div值進行歸一化處理并將其投影到［0，1］區間，得到概率P。如式（7）所示，當Div越小表示種群多樣性越高，概率P值就越小，反之種群多樣性越低則概率P值就越大。

P=exp（－11+Div）（7）

DMEFPA以概率P使用如式（8）所示的質心反向學習策略［20］對所有個體生成其反向個體，再按適應度篩選較優的個體以獲得新的種群并重新劃分子群。質心反向學習公式如下：

X*i=2Xm－Xi（8）

其中：Xi為種群個體；Xm為種群的質心；X*i為個體對應的反向個體。使用質心反向學習的目的是圍繞種群的質心進行反向學習，可以使獲得的個體反向解更傾向于探索種群外空間，以增強種群跳出局部最優能力。

上述依據種群離散度指標Div值來決定是否重新劃分種群方法的核心思想是：當種群多樣性降低時，各子群更趨向于相同的方向探索，則以概率P隨機重新生成更高質量的種群并重新劃分子種群，可以增強算法跳出局部最優的能力并提高算法的全局尋優性能。

2.2 子種群的個體遷移策略

文獻［21］指出為多子種群構建有效的信息共享方式，能夠使子群在共享信息中獲益并更徹底地探索其所在搜索空間。構建個體遷移方式通常存在兩種子群的拓撲構成形式：靜態拓撲和動態拓撲。在靜態拓撲當中，子種群間的信息交流方式是按固定順序依次對各個子種群進行個體遷移。由于子種群間信息交換方式持續固定的路徑，所以可能導致子種群的多樣性損失較大。動態拓撲形式利用隨機順序構成動態拓撲，所以各個子種群間完全是隨機選擇其他子種群進行個體遷移，可以有利于提高子種群的多樣性。 基于上述分析，DMEFPA采用了一種基于環型拓撲的動態個體遷移策略進行3個子群間的個體遷移，以降低子群個體質量劣化的概率。

該動態個體遷移策略先將3個子群以隨機順序構成一個環型拓撲，如圖2所示。

再按環型拓撲結構依次從各子群中選出被遷移的個體，并將環型拓撲中該子群的下一個子群中適應度值最差的個體替換為選出的遷移個體。如圖2所示，先從子群2中選出被遷移的個體來替換子群1中適應值最差的個體，完成一次子群間的個體遷移。按環型拓撲依次進行，直到子群2的適應值最差的個體被從子群3中選出的遷移個體替換為止。每個子群中的遷移個體都使用依據個體適應度值的隨機機制選出。該隨機遷移個體選出機制首先分別對每個子群內的個體依據其適應度值進行由小到大的排序，設子群中個體在按適應值排序后的序號為Si，然后按式（9）計算個體的權重αi：

αi=2β×e（-β×（Si-1））N×（1+e（-β×（Si-1）））2（9）

其中：N為該子群的大小；β為權重變化控制因子。通過權重計算個體被選為子群的遷移個體的概率Gi=αi/（α1+…+αN）。如式（9）所示，個體的適應值排序序號Si越小，其權重αi就越大，該個體被選為子群的遷移個體的概率就越大，從而下一子群中適應度值最差的個體就越可能被上一子群中更好的個體替換。該動態個體遷移策略的基本思想是淘汰每個子群中適應度最差的個體并引入其他子群中適應值較優的個體，以維持種群的個體質量。該策略也符合適者生存的自然選擇原則。

為觀察式（9）中參數β對個體權重αi大小的影響，圖3繪制了個體權重αi隨著個體適應度排序序號Si以及參數β的變化曲線圖。觀察圖3可以發現：β的值越大，個體權重αi隨適應度排序的增加而快速下降，從而適應度排序靠前的個體占據了絕大部分被選中的概率，導致選擇的遷移個體擁有較好的適應度值以增強子群多樣性，并可以防止子群向已知最優個體快速收斂。反之，β的值越小，個體權重αi隨適應度排序的增加緩慢下降，導致適應度排序靠后的個體被選中的概率相對偏高，但有助于子群保持高度的搜索多樣性并消減了子群陷入局部最優的風險。基于上述考慮，DMEFPA將參數β設立為0.4，可以使遷移個體增強子群的多樣性同時還降低了子群陷入局部最優的風險。

最后，個體遷移策略的使用頻率過大或過小都將對算法性能進行損害。文獻［21，22］通過實驗表明子群間信息交流頻率為50最佳，即算法每50次迭代進行一次信息交流，有利于保持種群多樣性的同時能夠獲得更好的收斂性能，所以本文提出的個體遷移策略頻率也設置為50。

DMEFPA采用的個體遷移機制能夠和多種群機制形成良好的互補。如圖1（a）展示了只使用適應度選擇個體進行子種群劃分的弊端。在圖1（a）中，適應度較優的個體全集中在圖的左半區域，且適應度值最優的幾個個體分別陷入三個局部中，導致被劃分出的3個子種群在圖1（a）中大致分為上、中、下三層。圖1（b）顯示了利用本文提出多種群劃分方法的子種群劃分的結果。該劃分方法將整個種群劃分為了3個較為均勻散布的子種群，可以使算法能夠更加全面地探索解空間。同時，采用動態拓撲結構的子種群間的個體遷移機制可以在擁有不同進化方向的子群間進行信息的相互交流，有利于對解空間的探索和開發，且避免子種群陷入局部最優導致種群停滯進化。

2.3 改進局部搜索策略

對FPA的局部尋優式（3）進行分析可以發現，個體的局部尋優方式是由子群內兩個隨機個體的差分向量引導的，導致此種單個突變算子的搜索范圍有限。當算法面臨多峰目標函數時，單個突變算子存在全局與局部搜索能力之間的平衡問題。在將種群劃分為多子群后，子群的搜索范圍縮小將導致單個突變算子的開發局部區域能力進一步受限。為增強算法對局部區域的開發，受三角變異的啟發［23］，本文提出一種改進的局部搜索策略，如式（10）所示。

Xt+1i=Xti+ε（Xtj－Xtk）+ε（Xtb－Xtw）（10）

其中：Xtj和Xtk是子群中隨機挑選的兩個個體；Xtb、Xtw分別是子群中適應度值的最優個體和最差個體；ε是［0，1］均勻分布的隨機數。

原FPA的局部搜索策略所使用的變異向量在隨機個體相近或搜索空間較小的情況下，會導致個體搜索區域相對較小，并且使用兩個隨機個體變異存在一定的盲目性。式（10）在原局部搜索方法的基礎上為其添加一個最佳最差變異向量。即式（10）對應的改進局部搜索策略右邊第一項為隨機差分項，第二項為最佳最差指導項。由于變異向量決定了探索區域的范圍，增加最佳最差變異向量可以使其探索區域更大，且利用了最佳個體的附近區域。隨機差分項具有較強的全局搜索能力，有利于擺脫局部最優陷阱；最佳最差指導項具有較強的局部搜索能力，能夠提升收斂速度。因此，改進的局部搜索策略在全局和局部搜索能力之間保持適當的平衡。

2.4 算法流程

本文提出基于動態多種群機制的增強花授粉算法（DMEFPA）的偽代碼如下所示。

輸入：算法最大迭代次數Maxiter；種群大小pop；切換概率p；搜索上界ub和下界lb；問題維度dim。

輸出：全局最優個體best及其適應度值f（best）。

1 初始化種群個體，評估每個個體適應度值并記錄最優個體；

2 while tlt;Maxiter

3 if t=1

4" for m=1∶pop；

5"" 按照式（5）計算出排名前的n個中心個體并為個體創建集和S*i中；

6" end for

7" for k=1∶N-n

8"" 將種群中除中心個體外的所有個體劃分到相距最近的集合S*i中完成多子群劃分；

9" end for；

10 end if

11 for j=1∶n //遍歷所有子群

12" for i=1∶length（S*i） //遍歷子群內全部個體

13"" if randgt;p

14""" 子群中個體通過式（1）進行全局尋優階段；

15"" else

16""" 子群中個體通過式（13）進行局部尋優階段；

17"" end if

18"" if f（Xt+1）gt;f（Xt）； Xt=Xt+1；

19"" end if；

20" if f（Xt+1）gt;f（best）；Xt=Xt+1；

21" end if

22" end for;

23 end for

24 if 0=mod（t，50） //每50次迭代使用一次個體遷移策略

25 將所有子群S*i通過隨機順序構成環型拓撲；

26 通過適應度值排序利用式（11）為個體賦予權重，隨后利用式（12）計算個體遷移概率并生成隨機數選擇遷移個體；

27 end if

28 if rand≤P //隨機數小于接受概率P

29 利用質心反向學習生成反向解并保持適應度更優個體

30 返回步驟4～9 //重新劃分子群

31 end if

32 t=t+1

33 算法是否達到最大迭代次數，是則退出循環，否則返回步驟11；

34 end while

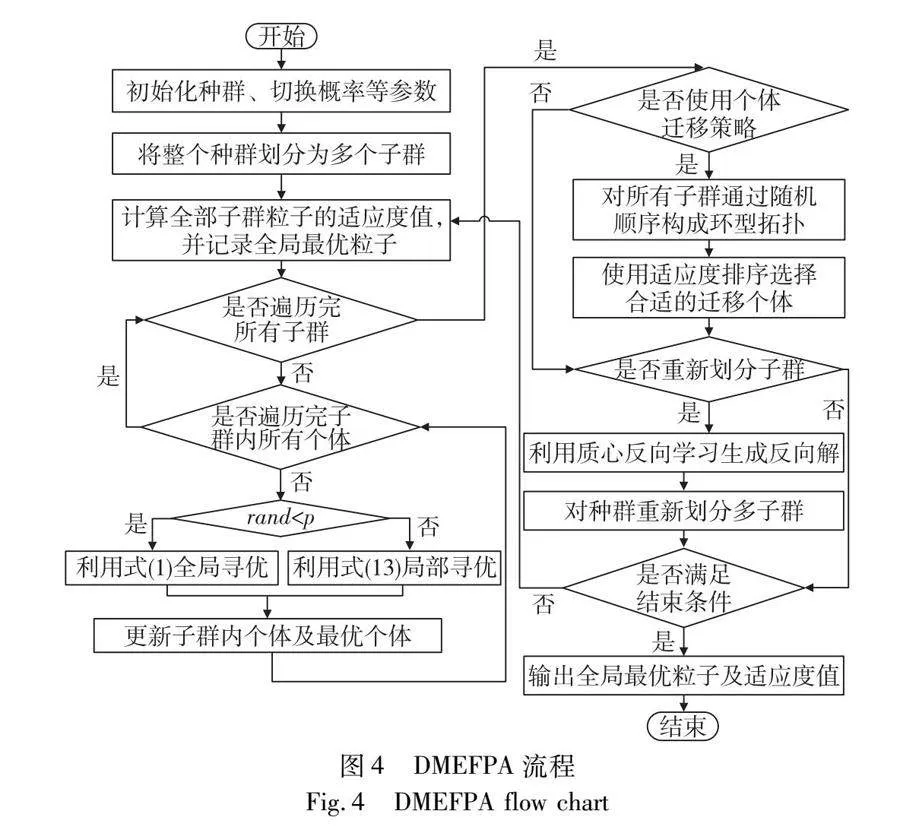
圖4展示了DMEFPA的流程。

2.5 DMEFPA時間復雜度分析

設初始種群大小為N，子種群數量為n（n=3），解空間維度為D，最大迭代次數T，多子群遷移次數t，多子群劃分次數為m。FPA的時間復雜度為O（N×D×T）。對整個種群進行初始化并評估每個個體的適應度值的時間復雜度為O（N×D+N）。利用適應度值結合距離挑選種群中心個體并圍繞其劃分多種群的時間復雜度為O（N log N×D×m），通過實驗發現子群在劃分次數僅占最大迭代次數的小部分。通過多樣性指標檢驗種群間多樣性情況是否重新劃分子群的時間復雜度為O（N×D×T）。所有子群中個體進行全局尋優或局部尋優的時間復雜度為O（N×D×T），各子群構成動態環型拓撲并通過適應度排序進行個體遷移的時間復雜度為O（N log N×D×t）。綜上所述，DMEFPA的時間復雜度為O（N×D×T）+O（N log N×D×m）+O（N×D×T）+O（N×D×T）+O（N log N×D×t）=O（N×D×T）。DMEFPA與原FPA時間復雜度在同一數量級。

3 實驗結果和分析

3.1 基準函數選取

為測試DMEFPA算法的性能，選取CEC2017標準測試集中的12個測試函數來測試算法的收斂速度和搜索精度。選取的標準測試函數分為4類，包括1個單峰函數（F1）、3個多峰函數（F2～F4）、4個混合函數（F5～F8）以及4個復合函數（F9～F12）。除單峰函數外的其余測試函數均存在大量局部最優點。測試函數類型、測試函數名及全局最優值詳情如表1所示。

3.2 實驗設計

為測試DMEFPA性能，將其與HLFPA［8］、WOFPA［11］、SCFPA［14］、AMSSA［15］、SHSSA［16］在上述的12個測試函數上進行實驗評估。為保證實驗的公平性，所有的仿真實驗均在同一環境下完成：實驗仿真軟件使用MATLAB R2022b，操作系統為Microsoft Windows 11，硬件配置為Intel Core i7-12700H 2.3 GHz，16 GB內存。所有算法的種群數量統一設定為50、迭代次數為500、所有算法單獨運行次數為30、搜索空間上下界為［-100，100］D。

測試中使用平均值Mean（均值越小表明該算法尋優能力更強），標準差Std（標準差越小表明算法魯棒性越強）作為評估算法性能優劣的指標，同時將Mean作為首要性能評價指標，其次為Std。對比結果采用排名Rank表示，Count表示算法累計獲得性能排名第一的次數，算法平均性能排名使用Ave Rank，整體性能排名為Total Rank。

3.3 測試結果

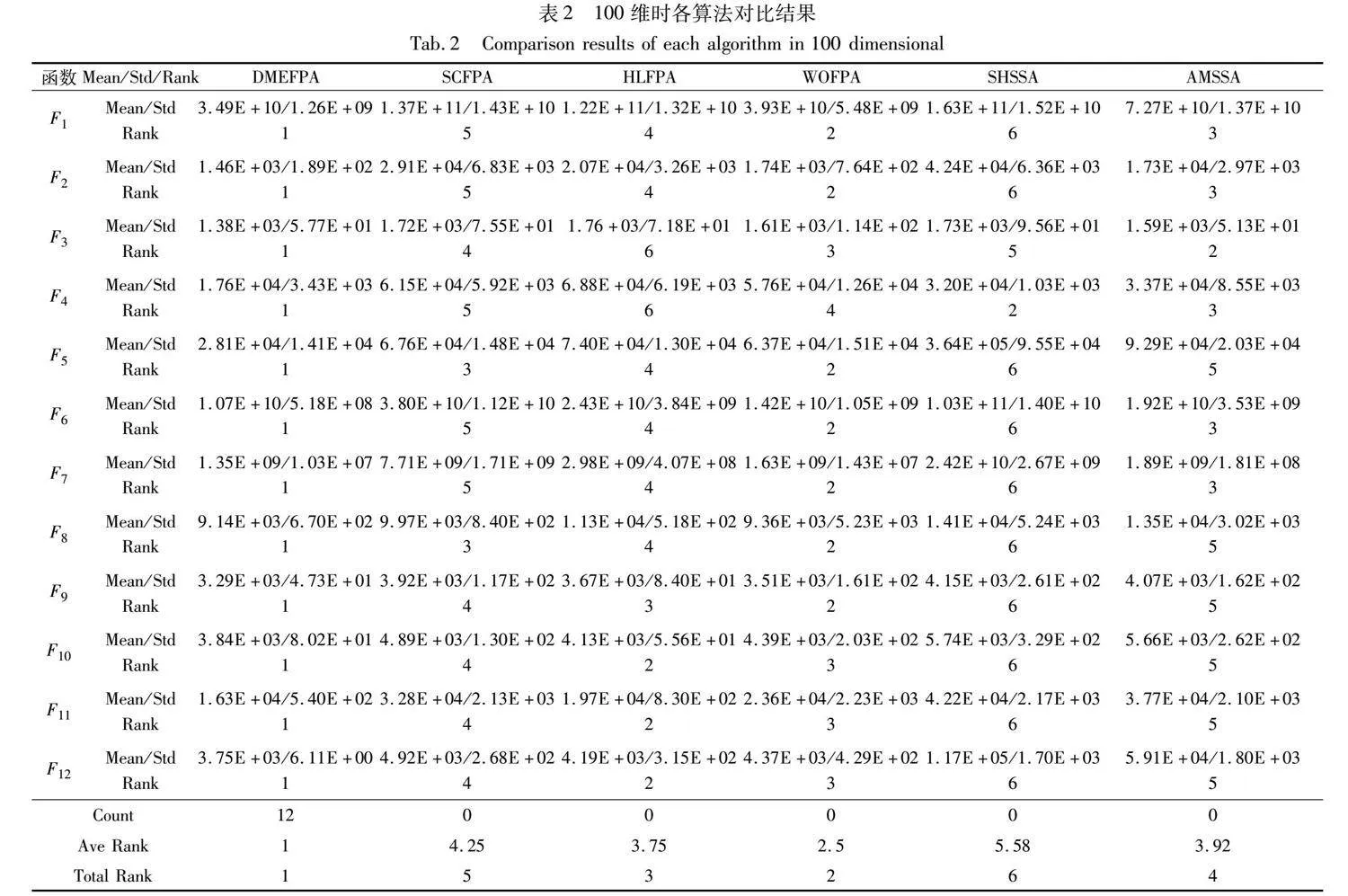
表2列出了各算法在12個測試函數在100維情況下的實驗數據，通過表2可以看出DMEFPA在100維的測試環境下Court次數最多，表明其在多個測試函數上均取得第一，同時DMEFPA在Ave Rank與Total Rank兩項指標上也都取得第一。這表明DMEFPA算法面對高維測試函數時相較于其他改進算法擁有更好的優化性能。同時DMEFPA對于目標函數的標準差Std也領先其他改進算法，這表明DMEFPA算法擁有更強的魯棒性。

對于單峰函數F1，DMEFPA也具有遠領先其他函數的收斂速度，該結果表明DMEFPA對于高維的單峰函數具有相較于其他改進算法更好的收斂性能。對于其余測試函數均取得了巨大的提升，如在測試函數F3、F4、F5、F12中比排名第二的算法提升了13%、55%、56%、11%。該事實表明相比其他改進算法，DMEFPA能夠對于擁有多個局部最優的高維多峰函數也能獲得更為出色的尋優能力。

如表2所示，對于指標Std，DMEFPA在函數F3、F4、F5、F8、F10上略次于其他改進算法，而在剩下7個測試函數上均獲得第一名的優異表現，這表明DMEFPA在高維復雜多峰目標函數上具有比其他FPA改進算法更好的魯棒性。

3.4 基于置信區間的收斂曲線圖的對比分析

置信區間作為一種統計方法，展現了樣本的真實值以一定概率落在測量結果周圍的程度。其計算方法如下：

CI=Mean±z×Stdn（11）

其中：CI為置信區間；Mean為樣本均值；z為臨界值，代表置信水平，本文設置為95%的置信水平；Std為樣本標準差；n為樣本大小。為展示本文算法收斂速度和精度，在得到各被測試算法的平均收斂曲線的前提下，設置每30次迭代展現各算法的置信區間。置信區間的大小可以代表算法的收斂速度和收斂精度。即置信區間寬度越小，算法的收斂精度越高，而在同一迭代次數下，置信區間位置越低，則算法的收斂速度越快。

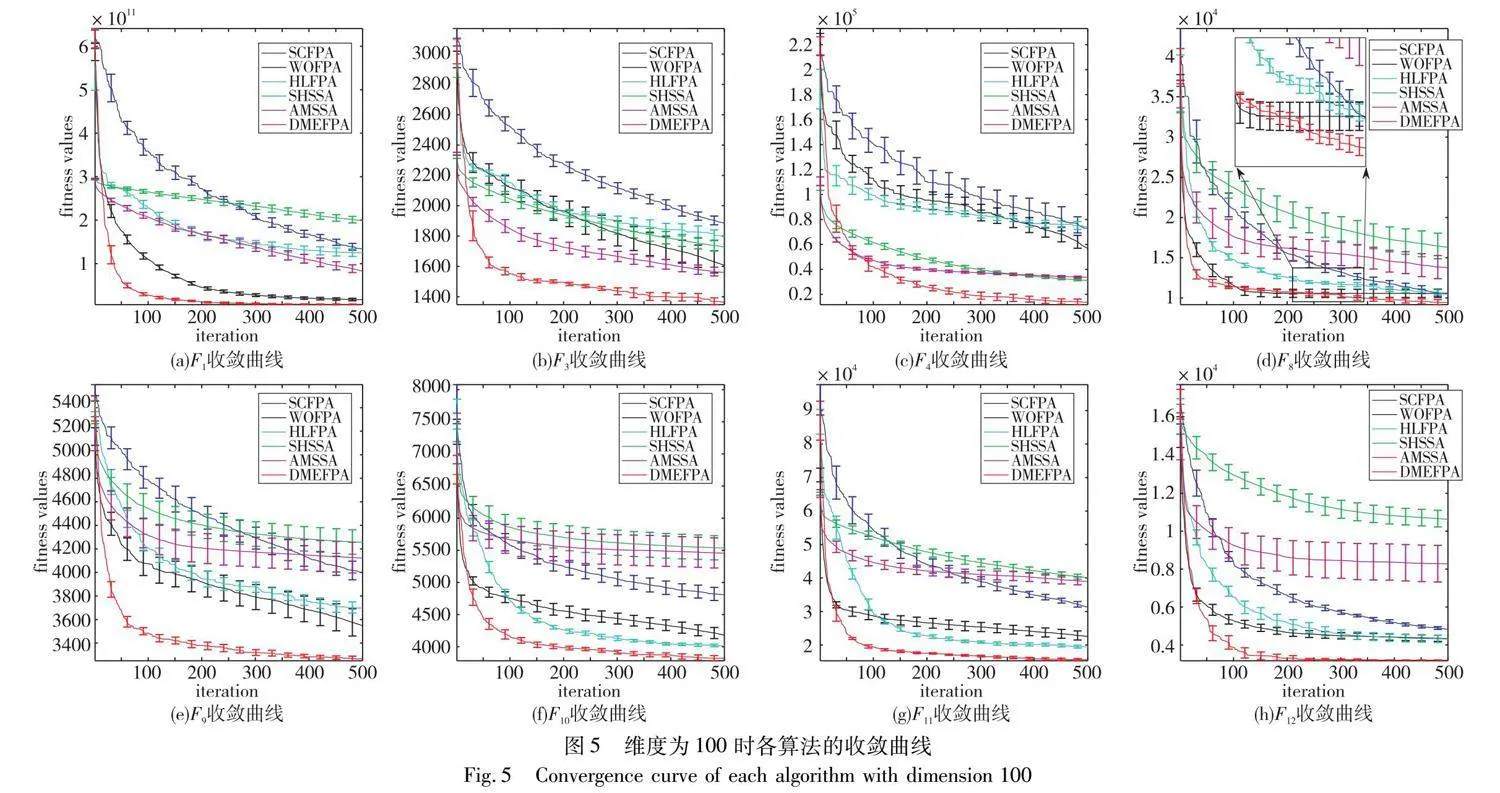
圖5列出了DMEFPA和改進算法對上述測試函數在100維情況下的部分測試函數帶置信區間的收斂曲線圖。如圖5所示，對多數測試函數，當其他改進算法在迭代后期陷入局部最優時，DMEFPA仍然能夠跳出局部最優，仍然能夠繼續探索全局最優，且從圖5中能夠發現，DMEFPA的置信區間相較其他算法都寬度更窄且位置更低。這表明DMEFPA在收斂精度與收斂速度方面具有更大的優越性。

從不同函數類別來看，沒有局部最優陷阱的單峰測試函數F1可以考驗各個算法的尋優能力。因為各算法在函數F1上沒有陷入局部最優的風險，所以各算法都能夠在迭代前中期發現全局最優并快速收斂。DMEFPA相較其他算法在迭代前期就快速向全局最優收斂并獲得出色的收斂速度。原因可能是采用基于適應度結合距離對種群進行劃分，使被劃分的3個子群能夠相對均勻分散在整個解空間，從而增強了算法的尋優能力。存在大量局部最優陷阱的多峰測試函數F2～F4可以考驗各算法保持種群多樣性和跳出局部最優的能力。DMEFPA相較其他改進算法，其迭代前期依靠均勻分散在解空間的多子群向全局最優快速收斂，在迭代后期其他改進算法陷入局部最優時，DMEFPA仍然能夠繼續優化，這可能是由于子群間的相互信息交流幫助不同子群跳出局部最優，并且改進后的局部搜索策略存在更強的變異能力導致的。對于混合測試函數F5～F8，DMEFPA迭代前期的收斂速度就明顯快于其他改進算法，而迭代后期由于DMEFPA的種群多樣性優于其他改進算法，從而可以獲得更高的收斂精度。對于組合測試函數F9～F12，當其他改進算法陷入局部最優無法向下迭代時，DMEFPA可以利用子群間的信息交流，并在動態步長和改進局部搜索策略幫助下繼續向更優解空間探索，從而獲得更高的尋優精度。

3.5 基于箱線圖的對比分析

圖6展現了DMEFPA和改進算法對上述部分測試函數在100維時獨立執行30次后獲得的箱型圖。在箱型圖中，箱體中的紅色線條代表中位數，箱體的上界與箱體的下界分別為整體數值的上四分位數與下四分位數；其次箱體兩頭的虛線代表了數據的離散程度，虛線越長代表數據越分散；最后，箱體外側的紅色符號+代表異常值，異常值越少說明算法穩健性越強。從圖6中可以看出，除F3外，DMEFPA的箱體均比其他改進算法的箱體更扁，這表明DMEFPA的最優值波動幅度不大，其魯棒性也更好。同時，DMEFPA的箱體下界同樣比其他改進算法更低并且中位線也低于其他改進算法，并且除F11外DMEFPA的箱型圖中的離群值相較于其他改進算法也較少，這表明DMEFPA擁有更高的收斂精度。以上事實表明DMEFPA極大增強了算法的尋優能力和穩定性。

3.6 完整性消融實驗

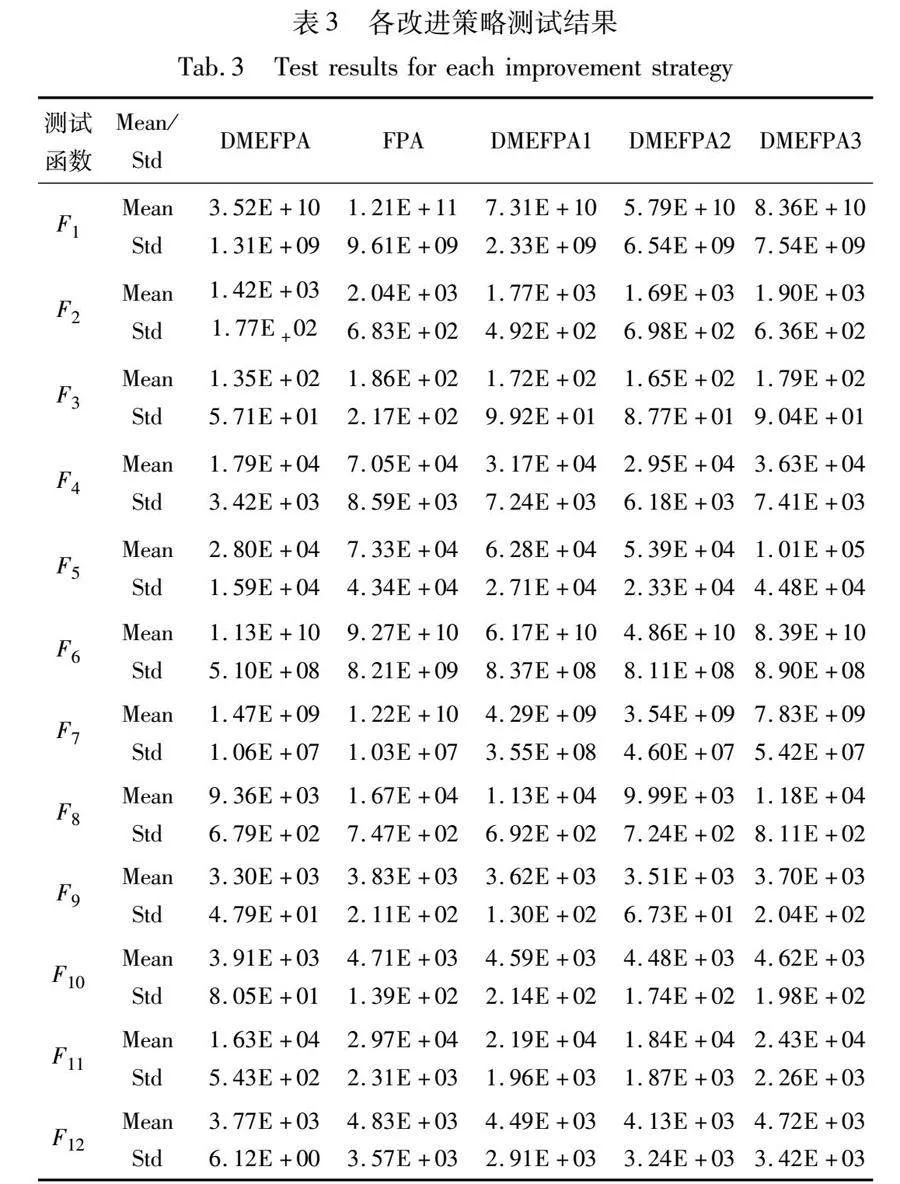
為展現DMEFPA使用策略的有效性，對DMEFPA中的各策略還進行了完整性消融實驗。設DMEFPA中對FPA中僅采用多子群策略的算法為DMEFPA1，對同時采用多子群策略和個體遷移策略的算法為DMEFPA2，對采用多子群策略并使用改進局部搜索方法的算法為DMEFPA3。將標準FPA和DMEFPA1、DMEFPA2、DMEFPA3使用表1中列出的測試函數進行性能測試。每個算法獨立運行10次，算法的迭代次數為500，其余算法詳細參數與3.2節中的設置相同。表3列出了測試的數據。

如表3所示，使用多子群方法的DMEFPA1以及多子群采用個體遷移策略的DMEFPA2在12個測試函數上都優于FPA，使用多子群算法同時增強子群間的信息交流的DMEFPA2在12個測試函數上都優于DMEFPA1及DMEFPA3。上述的結果表明多子群方法可以有效地增強算法的尋優性能，并且增強子群間的信息交流也能提升子群的多樣性。同時，僅使用多子群策略和改進局部搜索方法的DMEFPA3性能提升不大，該事實表明使用個體遷移策略配合多子群策略能夠有效地提升多子群的有效性。對于DMEFPA，其收斂精度高于其他參與測試的算法，表明DMEFPA所提出的各個改進策略對提升算法性能能發揮不可或缺的作用。

3.7 Friedman檢驗

為進一步驗證DMEFPA算法與其他5種算法的顯著性差異，將6種算法運行30次得到的平均值采用Friedman檢驗，檢驗結果如表4所示。若表中的P-value值小于0.01，則表明算法間存在顯著性差異。表4中除P-value以外的其他值為各算法的秩平均值。如表4所示，對于30維、50維、100維，DMEFPA的P-value分別為2.68E-09、1.49E-09、3.29E-09均遠小于0.01，這表明DMEFPA相較其他改進算法存在較大的顯著性差異。在不同維度中，DMEFPA的秩平均值也都小于其他算法，這反映了DMEFPA的性能是最優的。綜上所述，DMEFPA的尋優能力在統計學上相較于其他改進算法存在明顯提升。

4 結束語

針對FPA容易陷入局部最優、算法早熟和收斂精度低等缺點，本文提出了一種基于動態多種群機制的增強花授粉算法DMEFPA。DMEFPA采用的動態多種群策略首先利用適應度值結合距離信息挑選子群中心，并將剩余個體劃分到距離最近的子群中心的方法完成多子群劃分，再依據概率接受是否生成新種群并重新劃分子種群。該策略可以增強種群多樣性并提升算法尋優能力。DMEFPA的動態多種群策略還引入了個體遷移機制，以保持子群個體的整體質量，并降低算法陷入局部最優的概率。此外，DMEFPA還采用了改進局部搜索策略進一步提升算法的尋優能力。12個CEC2017測試函數的實驗結果表明，相比參與測試的其他5個改進算法，Friedman算法可以獲取最優的性能。未來計劃對DMEFPA進行進一步的改進，并將其應用于解決多目標問題，探索DMEFPA算法面對復雜的工程應用問題等復雜優化問題的可能性。

參考文獻：

［1］Yang Xinshe. Flower pollination algorithm for global optimization ［C］// Proc of International Conference on Unconventional Computing and Natural Computation. Berlin： Springer， 2012： 240-249.

［2］Alyasseri Z A A， Khader A T， Al-Betar M A， et al. Multi-objective flower pollination algorithm： a new technique for EEG signal denoi-sing ［J］. Neural Computing and Applications， 2023， 35： 7943-207962.

［3］Gupta S K， Dalal A. Optimisation of hourly plants water discharges in hydrothermal scheduling using the flower pollination algorithm ［J］. International Journal of Ambient Energy， 2023， 44（1）： 686-692.

［4］Chen Yang，Pi Dechang，Xu Yue. Neighborhood global learning based flower pollination algorithm and its application to unmanned aerial vehicle path planning ［J］. Expert Systems with Applications， 2021， 170： 114505.

［5］肖輝輝， 萬常選. 基于多策略的改進花授粉算法 ［J］. 軟件學報， 2021， 32（10）： 3151-3175. （Xiao Huihui， Wan Changxuan. Improved flower pollination algorithm based on multi-strategy ［J］. Journal of Software， 2021， 32（10）： 3151-3175.）

［6］肖輝輝， 萬常選， 段艷明， 等. 融合高斯變異和Powell法的花朵授粉優化算法 ［J］. 計算機科學與探索， 2017， 11（3）： 478-490. （Xiao Huihui， Wan Changxuan， Duan Yanming， et al. Flower pollination algorithm combination with Gauss mutation and Powell search method ［J］. Journal of Frontiers of Computer Science and Technology， 2017， 11（3）： 478-490.）

［7］寧杰瓊， 何慶. t-分布擾動策略和變異策略的花授粉算法 ［J］. 小型微型計算機系統， 2021， 42（1）： 64-70. （Ning Jieqiong， He Qing. Flower pollination algorithm based on t-distribution perturbation strategy and mutation strategy ［J］. Journal of Chinese Computer Systems， 2021， 42（1）： 64-70.）

［8］洪露， 賀興時， 楊新社. 基于三重動態調整的花授粉算法 ［J］. 西安工程大學學報， 2021， 35（2）： 97-103. （Hong Lu， He Xingshi， Yang Xinshe. The flower pollination algorithm based on triple dynamic adjustment ［J］. Journal of Xi’an Polytechnic University， 2021， 35（2）： 97-103.）

［9］張水平， 高棟. 基于動態調整和協同搜索的花授粉算法 ［J］. 計算機工程與應用， 2019， 55（24）： 46-53. （Zhang Shuiping， Gao Dong. Flower pollination algorithm based on dynamic adjustment and cooperative search ［J］. Computer Engineering and Applications， 2019， 55（24）： 46-53）

［10］Wang Zhongmin， Luo Qifang， Zhou Yongquan. Hybrid metaheuristic algorithm using butterfly and flower pollination base on mutualism mechanism for global optimization problems ［J］. Engineering with Computers， 2021， 37： 3665-3698.

［11］Tawhid M A， Ibrahim A M. Solving nonlinear systems and unconstrained optimization problems by hybridizing whale optimization algorithm and flower pollination algorithm ［J］. Mathematics and Computers in Simulation， 2021， 190： 1342-1369.

［12］Al-Betar M A， Awadallah M A， Abu Doush I， et al. Island flower pollination algorithm for global optimization ［J］. The Journal of Supercomputing， 2019， 75： 5280-5323.

［13］陳西成， 劉曙， 范兵兵. 應用小生境混沌搜索策略的花朵授粉算法 ［J］. 重慶大學學報， 2018， 41（11）： 92-99. （Chen Xicheng， Liu Shu， Fan Bingbing. Flower pollination algorithm with niche chaotic search strategy ［J］. Journal of Chongqing University， 2018， 41（11）： 92-99.）

［14］張超， 楊憶. 引入正弦余弦算子和新自花授粉的花授粉算法 ［J］. 西 安工程大學學報， 2023， 37（2）： 119-129. （Zhang Chao， Yang Yi. Flower pollination algorithm with introduced sine cosine operator and new selfpollination method ［J］. Journal of Xi’an Polytechnic University， 2023， 37（2）： 119-129.）

［15］蘇瑩瑩， 王升旭. 自適應混合策略麻雀搜索算法 ［J］. 計算機工程與 應用， 2023， 59（9）： 75-85. （Su Yingying， Wang Shengxu. Adaptive hybrid strategy sparrow search algorithm ［J］. Computer Engineering and Application， 2023， 59（9）： 75-85.）

［16］陳功， 曾國輝， 黃勃， 等. 螺旋探索與自適應混合變異的麻雀搜索算 法 ［J］. 小型微型計算機系統， 2023， 44（4）： 779-786. （Chen Gong， Zeng Guohui， Huang Bo， et al. Sparrow search algorithm with spiral exploration and adaptive hybrid mutation ［J］. Journal of Chinese Computer Systems， 2023， 44（4）： 779-786.）

［17］Chaudhary R， Banati H. Study of population partitioning techniques on efficiency of swarm algorithms ［J］. Swarm and Evolutionary Computation， 2020， 55： 100672.

［18］Wang Zijia，Yang Qiang，Zhang Yuhui， et al. Superiority combination learning distributed particle swarm optimization for large-scale optimization ［J］. Applied Soft Computing， 2023， 136： 110101.

［19］Zhang Daren，Ma Gang，Deng Zhuoran， et al. A self-adaptive gradient-based particle swarm optimization algorithm with dynamic population topology ［J］. Applied Soft Computing， 2022， 130： 109660.

［20］Li Jiahang，Gao Liang，Li Xinyu. Multi-operator opposition-based learning with the neighborhood structure for numerical optimization problems and its applications ［J］. Swarm and Evolutionary Computation， 2024， 84： 101457.

［21］Thaher T， Sheta A， Awad M， et al. Enhanced variants of crow search algorithm boosted with cooperative based island model for global optimization ［J］. Expert Systems with Applications， 2024， 238： 121712.

［22］Awadallah M A， Al-Betar M A， Bolaji A L， et al. Island artificial bee colony for global optimization ［J］. Soft Computing， 2020， 24（17）： 13461-13487.

［23］Mohamed A W. An improved differential evolution algorithm with triangular mutation for global numerical optimization ［J］. Computers amp; Industrial Engineering， 2015， 85： 359-375.

［24］Shen Ya， Zhang Chen， Gharehchopogh F S， et al. An improved whale optimization algorithm based on multi-population evolution for global optimization and engineering design problems ［J］. Expert Systems with Applications， 2023， 215： 119269.

［25］李大海， 伍兆前， 王振東. 多策略增強花授粉算法及其應用 ［J］. 計算機應用研究， 2022， 39（8）： 2388-2396， 2402. （Li Dahai， Wu Zhaoqian， Wang Zhendong. Multi-strategy flower pollination optimization algorithm for vehicle power transmission parameters ［J］. Application Research of Computers， 2022， 39（8）： 2388-2396， 2402.）