基于CGCS2000的漳州城市坐標系探討

摘要：隨著原有的城市獨立坐標系被停用，2000國家大地坐標系（China Geodetic Coordinate System 2000，CGCS2000）的應用推廣，在城市日常規劃、建設、驗收等相關測繪作業中，存在實測距離直接投影到標準分帶的CGCS2000的長度形變不符合相關規范的問題。結合福建省漳州市中心城區的實際情況，探討了采用117°40′自定義中央子午線，以任意帶高斯投影于CGCS2000橢球建立漳州城市坐標系坐標系的合規性和可行性。

關鍵詞：城市坐標系 投影變形 2000國家大地坐標系 中央子午線

Exploration of Zhangzhou Urban Coordinate System Based on CGCS2000

GUO Mingjie

Zhangzhou Institute of Surveying and Mapping， Zhangzhou， Fujian Province，

363005 China

Abstract： With the discontinuation of the original urban independent coordinate system and the application and promotion of China Geodetic Coordinate System 2000（CGCS2000）， there is a problem that the length deformation of the CGCS2000 directly projected by the measured distance to the standard zoning does not comply with the relevant specifications in the daily urban planning， construction， acceptance and other related surveying and mapping operations. Combined with the actual situation of the central urban area of Zhangzhou， Fujian Province， it discuss the compliance and feasibility of using a 117°40′ custom central meridian to establish the coordinate system of Zhangzhou City with an arbitrary Gaussian projection on a CGCS2000 ellipsoid.

Key Words： Urban coordinate system; Deformation of projection; CGCS2000; Central meridian

自2008年7月1日起，我國正式啟用了2000國家大地坐標系（China Geodetic Coordinate System 2000，CGCS2000），極大地推動了我國高精度三維地心坐標框架和基準體系的建設，進一步滿足了經濟建設、科學研究和國防建設的需要，為各項社會經濟活動提供了基礎性保障。

漳州市位于福建省最南部，其陸域地處北緯23°34’～25°15’，東經116°54’～118°08′之間，南北長187 km，東西寬127 km。東南臨臺灣海峽，東北與廈門市、泉州市接壤，西北與龍巖市相連，西南與廣東省梅州市、潮州市毗鄰，面積12 607 km2。

本文將分析按照標準分帶117°確定中央子午線的CGCS2000是否會導致漳州中心城區的投影變形超限而無法滿足日常的工程測量的要求，分析建立基于CGCS2000的漳州城市坐標系。

1 CGCS2000 坐標系下長度投影變形分析

1.1投影變形的限差

根據《城市測量規范》（CJJ/T 8—2011）的要求，工程測量中平面控制網的坐標系統，應滿足測區內投影長度變形不大于2.5 cm/km，即相對誤差小于1/40 000[1]。

1.2投影變形問題的主要因素

投影長度變形主要由以下兩種因素產生。

（1）實量邊長歸算到橢球面上，長度縮短，其變形影響為Ds1。

式（1）中：Hm 為歸算邊高出橢球面的平均高程，s為歸算邊的長度，R為歸算邊方向橢球法截弧的曲率半徑，R的概略值為 6 370 km。

（2）橢球面上邊長歸算到高斯投影面上，長度增加，其變形影響為Ds2 。

式（2）中：s0 為投影歸算邊長，ym 為歸算邊兩端點橫坐標平均值，Rm為橢球面平均曲率半徑。

根據長度變形公式，投影長度變形量為觀測邊長歸化至參考橢球面的變形量和橢球面上的邊長投影至高斯平面的變形量之和，二者對長度的影響存在抵消關系，但對區域平均高程較低或測區距離中央子午線太遠時，完全抵消是不可能的。在實量邊長歸算到橢球面上時，影響因子主要為歸算邊的長度s及歸算邊高出橢球面的平均高程H m；在橢球面上邊長歸算到高斯投影面上時，影響因子主要為歸算邊兩端點橫坐標平均值ym及投影歸算邊長s0。

1.3 GCS2000坐標系下長度投影變形的計算

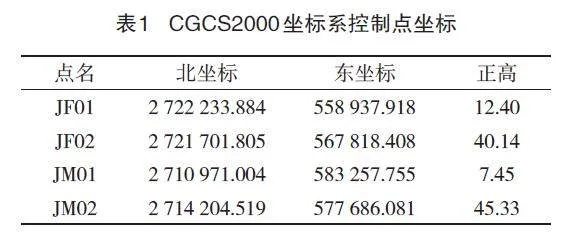
漳州市測繪設計研究院在漳州市中心城區金峰開發區及漳州臺商投資區布設了D級控制網，并通過聯測周邊C級控制點進行了D級網靜態觀測和解算。現分別選取金峰開發區控制網及漳州臺商投資區控制網的各一對點JF01-JF02和JM01-JM02，坐標值如表1所示，現采用以下兩種方法計算長度投影變形量。

1.3.1投影變形公式法

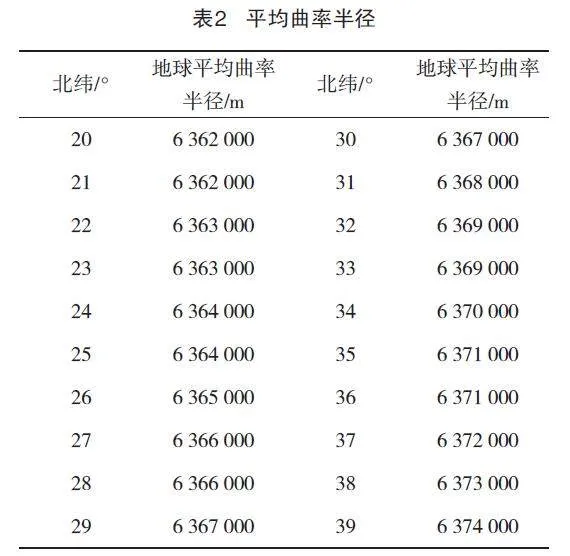
查找文獻可知不同緯度下的地球平均曲率半徑如表2所示。

（1）計算GCS2000坐標系下JF01-JF02的理論長度投影變形量。

已知JF01、JF02兩點的緯度在24°30′，經度在117°33′左右，R取6 364 000，平均橢球高為Hm=26.27 m，歸算邊長S及歸算投影邊長S0取靜態基線邊長為8 896.07 m，以及在CGCS2000坐標系下的坐標值。根據式（1），計算實量邊長歸算到橢球面上，其變形影響為Ds1=-0.04 m；根據公式（2），計算橢球面上邊長歸算到高斯投影面上，其變形影響為Ds2=0.41 m，綜合所得長度投影變形量DS=Ds1+Ds2=0.37 m，長度變形值為4.16 cm/km。

（2）計算GCS2000坐標系下JM01-JM02的理論長度投影變形量。

已知JM01、JM02兩點的緯度在24°30′，經度在117°45′左右，R取6 36 4000，平均橢球高Hm=26.39 m，歸算邊長S及歸算投影邊長S0取靜態基線邊長=6 441.52 m，以及在CGCS2000坐標系下的坐標值。根據公式（1），計算實量邊長歸算到橢球面上，其變形影響為Ds1=-0.03 m；根據式（2），計算橢球面上邊長歸算到高斯投影面上，其變形影響為Ds2=0.49 m，綜合所得長度投影變形量DS=Ds1+Ds2=0.46 m，長度變形值為7.14 cm/km。

1.3.2坐標反算法

計算靜態觀測的基線邊長與GCS2000坐標系下坐標反算的邊長的較差，比較2套成果下的投影變形大小。其較差情況如表3所示。

2 漳州城市坐標系的建立

2.1 城市坐標系的建立方法

由《城市坐標系統建設規范》（GB/T 28584—2012）可知，城市平面坐標系涉及參考橢球的選擇、中央子午線的確定、投影面高程和坐標系原點與定向等內容[2]。城市坐標系的建立方法，大致歸納為3種：第一種為高斯投影于參考橢球面上任意3°帶的平面直角坐標系，此種方法高程投影面采用CGCS2000參考橢球面，只移動中央子午線；第二種為高斯投影于抵償高程面的3°帶平面直角坐標系，此種方法不改變中央子午線，通過改變高程投影面抵消高斯投影變形；第三種為以中心點坐標平移或坐標加常數和旋轉的平面直角坐標系，此種方法以城市或測區中央某一控制點為中心點，將所有原控制點以中心基準點進行平移，然后按某角度旋轉，最后行程獨立坐標[3-6]。

漳州市中心城區的經度大致在117°40′左右，原漳州市坐標系是基于1954年北京坐標系建立的中央子午線為117°40′的城市直角坐標系，隨著CGCS2000的啟用，原漳州市坐標系已停止使用。綜合考慮漳州市中心城區的地理位置、經濟發展狀況，結合漳州國土空間總體規劃（2020—2035年），以及基于原漳州城市坐標系的歷史沿革，綜合考慮采用高斯投影于參考橢球面上任意3°帶的平面直角坐標系這一方法，以中心城區中央的117°40′為中央子午線，基于CGCS2000的漳州城市坐標系（以下簡稱漳州2000坐標系）[6-9]。

2.2 漳州2000坐標系下長度投影變形的計算

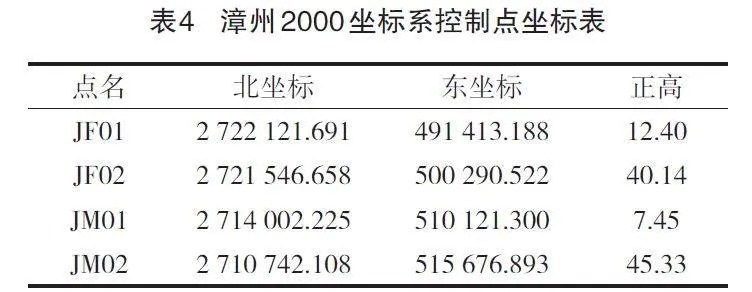
根據漳州2000坐標下解算出分別位于中心城區東西兩端的控制點坐標如表4所示。

2.2.1投影變形公式法

（1）JF01-JF02的理論長度變形量。

已知JF01、JF02兩點的緯度在24°30′，經度在117°33′左右，R取6 364 000，平均橢球高Hm=26.27 m，歸算邊長S及歸算投影邊長S0取靜態基線邊長=8 896.07 m，以及在CGCS2000坐標系下的坐標值。根據式（1），計算實量邊長歸算到橢球面上，其變形影響為Ds1=-0.04m；根據式（2），計算橢球面上邊長歸算到高斯投影面上，其變形影響為Ds2=0.003m，綜合所得長度投影變形量DS=Ds1+Ds2=-0.04m，長度變形值為0.45cm/km。

（2）JM01-JM02的理論長度變形量。

已知JM01、JM02兩點的緯度在24°30′，經度在117°45′左右，R取6 364 000，平均橢球高Hm=26.39 m，歸算邊長S及歸算投影邊長S0取靜態基線邊長=6 441.52 m，以及在CGCS2000坐標系下的坐標值。根據式（1），計算實量邊長歸算到橢球面上，其變形影響為Ds1=-0.03 m；根據式（2），計算橢球面上邊長歸算到高斯投影面上，其變形影響為Ds2=0.01 m，綜合所得長度投影變形量DS=Ds1+Ds2=-0.02 m，長度變形值為0.31 cm/km。

2.2.2坐標反算法

計算靜態觀測的基線邊長與漳州2000坐標系坐標反算的邊長的較差，比較2套成果下的投影變形大小。其較差情況如表5所示。

2.3 變形量對比

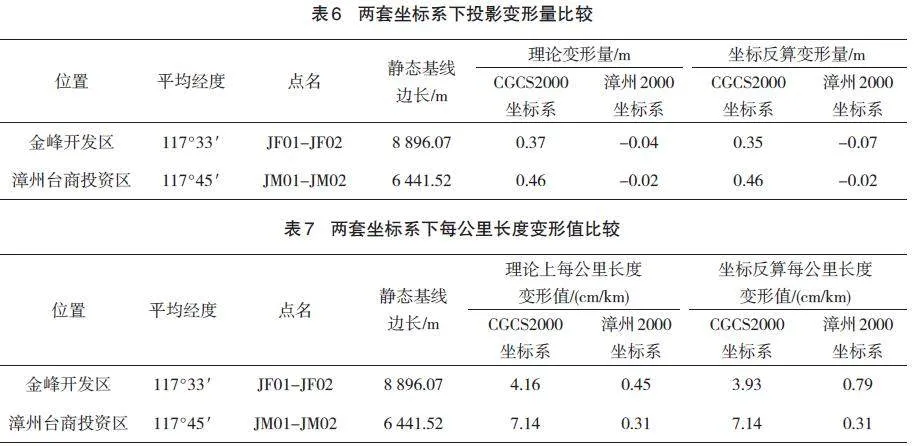
通過上文兩套坐標系下長度變形的計算，分析兩套坐標系下，兩段邊長的理論與實際投影變形量及每公里長度變形值的對比如表6、表7所示。

3 結語

漳州中心城區地形起伏不大，平均高程較低，距離中央子午線較遠，在城市測量作業中，如果直接采用2000國家大地坐標系坐標成果施測，中心城區每公里長度變形值均不滿足《城市測量規范》（CJJ/T 8—2011）要求。經過綜合分析，選擇了實用合理的城市坐標系建立方案，建立了中央子午線設置為117°40′的基于CGCS2000橢球的漳州城市坐標系，每公里長度變形值均滿足《城市測量規范》（CJJ/T 8—2011）要求，較好地解決了城市測量過程中長度投影變形的問題，既延續了原漳州坐標系相同的中央子午線，又保持了與CGCS2000成果的相對一致，有利于實現城市測量的準確性和地理信息成果的資源共享。

參考文獻

[1]住房和城鄉建設部.城市測量規范：CJJ/T8-2011[S].北京：中國建筑工業出版社，2011.

[2]國家質量監督檢驗檢疫總局，中國國家標準化管理委員會.城市坐標系統建設規范：GB/T 28584-2012[S].北京：中國標準出版社，2012.

[3]張現禮，陳星彤，王友雷，等.雄安新區城市坐標系的建立及應用[J].測繪與空間地理信息，2023（10）：171-174.

[4]蘭志武.基于CGCS2000 橢球的城市坐標系建立及應用[J].福建建筑，2016（3）：109-113.

[5]龍海奎，白鋒，任祺.建立基于CGCS2000城市坐標系的應用分析[J].城市勘測，2014（5）：111-113.

[6]馬波，張洪，朱月恒.建立城市坐標系的關鍵問題探討[J].地礦測繪，2021（4）：21-25.

[7]魏保峰，陳國平，李寧，等.昆明2000平面坐標系統設計與實現[J].地理空間信息，2023（5）：102-106.

[8]陳浩，趙峰，郭功舉，等.上海2000坐標系建立方法研究[J].工程勘察，2023（8）：61-66.

[9]徐益峰，張蒙.基于CGCS2000的蘇州平面坐標系建立[J].地理空間信息，2023（10）：120-122.