基于馬爾科夫決策過程理論的風電項目投資決策模型研究

摘 要：本文旨在探討基于馬爾科夫決策過程理論的風電項目投資模型構建及優化方法。通過綜合考慮政策支持、稅收環境、建設成本、風能資源和并網潛力等關鍵指標，利用馬爾科夫鏈技術對動態環境下的風電投資決策問題進行建模。研究采用值迭代算法進行循環迭代更新值函數V，并找到最優政策，從而實現長期規劃與效益最大化。結果顯示，在保持初始穩定策略下系統對特定狀態有明顯上升趨勢，值函數平滑上升展現算法在決策方面取得良好效果，在多次優化后逐漸接近局部最優解或全局最優解。

關鍵詞：馬爾科夫決策；風電項目投資；決策模型

中圖分類號：TM 732" " 文獻標志碼：A

風電項目投資涉及多方面因素和不確定性，采用馬爾科夫決策過程理論可以幫助制定有效的投資方案。翟保豫等[1]基于WRF模式和風速誤差修正構建中期風電功率預測方法，算例顯示該方法提升了精度且降低了預測誤差。張彬橋等[2]基于Copula函數的馬爾科夫鏈風速預測模型，在短期內對風速進行可靠性高精度預測。楊輝明等[3]改進馬爾科夫鏈的風電日前不確定性建模方法。劉大貴等[4]以熵值法組合單一灰色GM（1，1）和三次指數平滑后再使用馬爾科夫鏈修正準確、有效地推斷未來一年可用電量。樊盼盼等[5]融合多時段SCADA數據實現機組態勢評估與決策，在考慮歷史記錄、運行趨勢下開展有功功率短期預測，并采用機器學習技術構建準確時間序列，以評估系統狀態穩定程度。張文秀等[6]在源-網-荷不確定因素綜述下考慮系統運行影響，提出計及源-網-荷因素的MarovChain風能網絡關系可靠性檢驗方案，并成功驗證其可行性與效力。基于現有研究，本文旨在通過構建一個基于馬爾科夫決策過程理論的風電項目投資模型，探討如何優化資源配置、降低風險并提高回報。

1 模型構建

風電投資決策中引入馬爾科夫決策過程具有重要意義。風電項目的投資涉及長期性、不確定性和復雜性，需要考慮多個因素，例如市場變化、政策影響、技術發展等。通過引入馬爾科夫決策過程（Markov Decision Process，MDP），可以更好地建模這些動態環境下的決策問題，并制定相應的最優化戰略。

1.1 模型建立與狀態轉移

MDP是一種數學框架，適合描述具有隨機性和不確定性的決策問題，并能夠輔助制定最佳決策方案。對風電項目來說，當考慮預期所剩規劃步數約束時，可以使用MDP來建立一個動態條件下的模型。通過這個模型，在每個時間點上都可計算出選擇某種行動后可能獲得的效用值，并結合折扣因子來權衡當前收益與將來潛在回報之間的關系。

在MDP中，通常定義狀態、行動、獎勵函數和轉移概率函數等元素。其中，“狀態”指系統可能處于的各種情形，例如在風電投資領域，各種外部因素會導致項目收益波動，例如市場需求變化、政府補貼調整等。將這些因素作為狀態空間中的狀態，并根據其概率特征構建狀態轉移函數 P ，描述不同狀態之間轉換概率。由此，定義馬爾可夫決策過程。它可以被表示成一個四元組，如公式（1）所示。

M=（S，A，P，R） （1）

式中：M為馬爾科夫決策過程；S為狀態空間，即所有可能環境狀態的集合；A為動作空間，即智能體所有可選行動的集合；P為狀態轉移函數，在給定狀態下執行動作后系統轉移到下一個狀態的概率；R為回報函數，在給定狀態下執行動作后從環境立即獲得的回報值。

通常情形下，S和 A可以是離散或連續性質，并且有2種方式來描述狀態：平鋪表示和因子化表示。平鋪表示對每個狀態進行編號，并使用查表方法存儲完整的轉移函數，其儲存空間為|S|×|A|×|S|；而因子包括關于狀態轉移概率的更多信息并且能更有效地利用特征向量對每一個狀態進行描述。針對因子化方法，動態貝葉斯網絡對應狀態表達函數中其轉移函數則可以被表示為一個兩層有向無環圖，函數則分解為公式（2）。

（2）

式中：s為有向無環圖中的第一層節點狀態表示；s'為有向無環圖中的第二層節點狀態表示；α為A中的可選動作數值計算表示方式；xi為狀態變量，在定義范圍內取值；ui為非獨立狀態變量，即不與其他狀態變量相獨立的狀態變量。

因此，因子化的表達形式更高效、緊湊，在實踐中更常應用。

1.2 動作選擇與回報機制

針對每個可能狀態，在給定條件下選擇最優動作是關鍵挑戰之一。通過定義合適的行為空間 A和回報函數R，可以量化每次行動帶來的效果并評估所獲得回報。

在馬爾科夫決策過程中，廣義控制策略是指將某種概率分布映射到控制器上，并設置該決策為π。具體來說，在給定狀態下采取某項活動出現的概率如公式（3）所示。

π：S×A→[0，1] （3）

由此，這一決策π可以表達為π（s，α），代表在某個情形下選擇某項活動就會出現α的概率。而當確定性策略總是選擇相同活動，則稱該策略為確定，如公式（4）所示。

π：S×A→{0，1} （4）

考慮智能體的未來匯報，則其效用值如公式（5）所示。

（5）

式中：u（）為效用值；s0為起始狀態；R（）為一步內回報的效用值。

實踐中的時間成本等因素使項目通常具有一定時限性，對應馬爾科夫決策過程為僅考慮未來H步內決策，因此根據所采取不同步驟時刻不斷迭代計劃限時內期望累積回報值，如公式（6）所示。

（6）

式中：H為外部環境約束下對效用函數收斂條件予以約束的指定步數條件，不增加該環節則需要增加折扣因子γ來保證函數收斂。

MDP框架下針對長期規劃與效用最大化問題需要考慮如何定義系統可能處于的各種情形以及系統可以采取哪些操作，如何評估每次行為所帶來的即時獎勵，如何描述系統從一個狀態轉移到另一個狀態涉及的隨機性或不確定性，如何結合外部環境約束條件進行收斂分析，并確保算法穩健、有效地執行。

1.3 長期規劃與效用最大化

風電項目是長期投資，需要考慮未來累積收益以及時序依賴關系。利用馬爾科夫決策過程理論框架可計算在當前情形下采取何種措施才能使整體效益達到最大值，從而實現長遠規劃和持續增值。具體來說，當在動態條件下考慮預期剩余t規劃步數約束時，可以基于狀態s而非行動s0來制定策略，并得到相應的值函數。后續行動價值函數Qtπ（s，α）可以如公式（7）所示。

（7）

式中：γ為折扣因子；Vπt-1為最后一步的效用值。

MDP允許處理環境中存在隨機性和不確定性帶來的挑戰，當面臨突發事件或新信息時能快速調整策略，以適應變局并提高系統魯棒度。這種方法有助于制定更靈活、智能化并且具備長遠眼光的決策方案，特別是在需要對未知情況做出反應并保持系統穩健性方面發揮重要作用。

2 性能測試

2.1 模型構建

政府政策支持、稅收環境、風電項目的建設成本、風能資源以及并網潛力等指標是構建風電項目投資則決策主要變量，相應構建壁板兩體系結果見表1。

由此，對已有數據進行仿真試驗，以驗證所提出方法是否可以適應實際情形，并比較其效果。

2.2 循環迭代

模型定義投資回報率矩陣，表示不同狀態下采取不同行動所帶來的投資回報率。每一行代表一個狀態，每一列代表可選擇的動作，即不同類型的投資方案。初始選擇保守型投資策略，使用值迭代算法來更新值函數V，并找到最優政策。

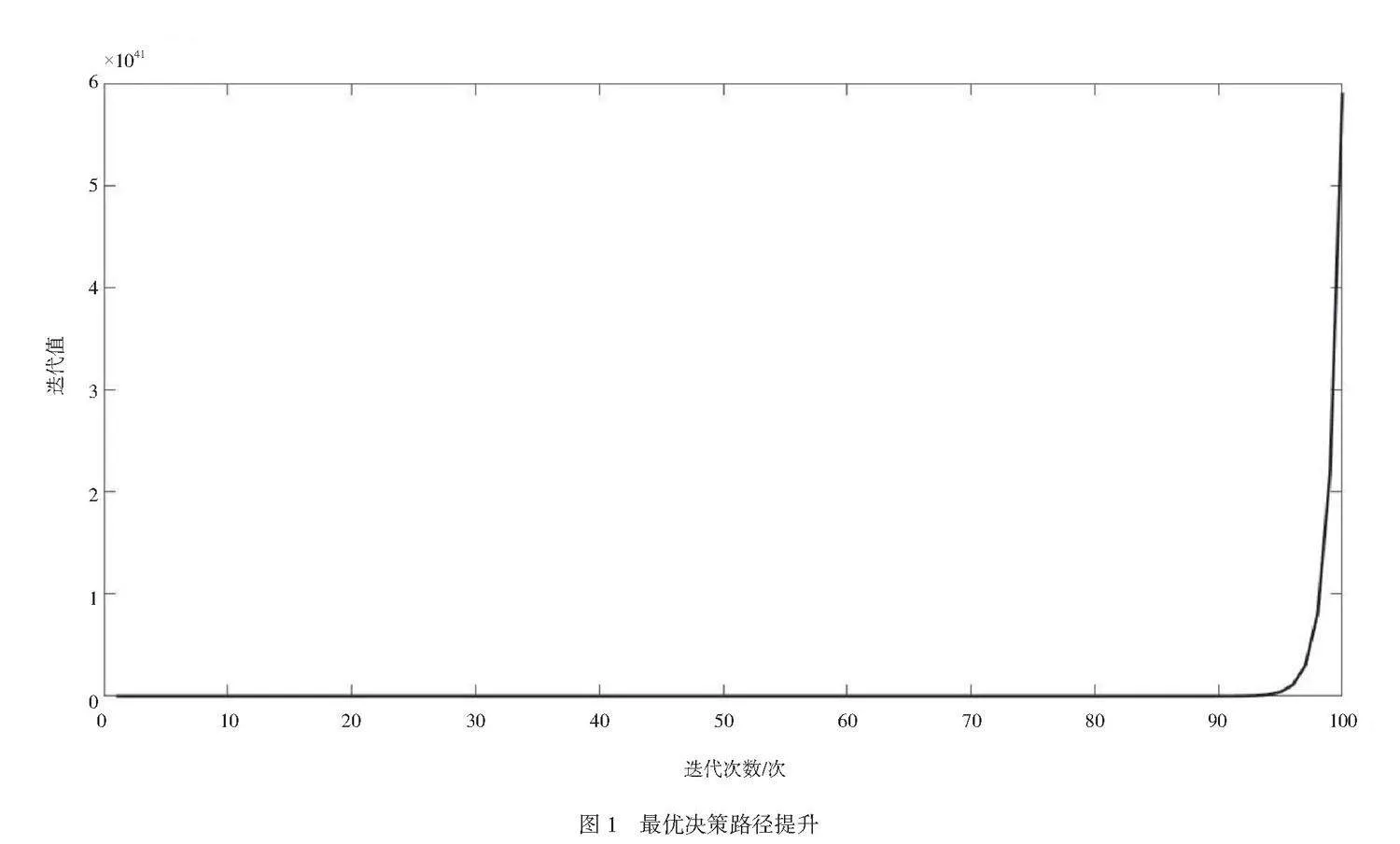
在每次循環中，在當前估計下計算Q-Value并根據Q-Value更新估計價值函數V。通過多次迭代得出近似收斂于真實價值函數或者最佳策略。由此，顯示輸出了經過模型運算得出的最優決策路徑序列如圖1所示。

由圖1可知，隨著迭代次數增加，可以觀察到值函數呈極平滑的上升趨勢。這種表現反映了馬爾科夫決策過程在優化決策方面取得了良好效果。系統持續地對問題領域進行多次決策優化后，逐漸接近一個局部最優解或全局最優解。這種穩定而持續的提升顯示算法在不斷改進其對環境特性和最佳操作選擇之間關系的理解，并表明模型有效地應用于風電投資領域。通過MDP框架，系統能夠實現智能化、自我學習與改進等目標，在長期風電項目中更準確地做出決策并不斷提高投資回報率。

2.3 結果分析

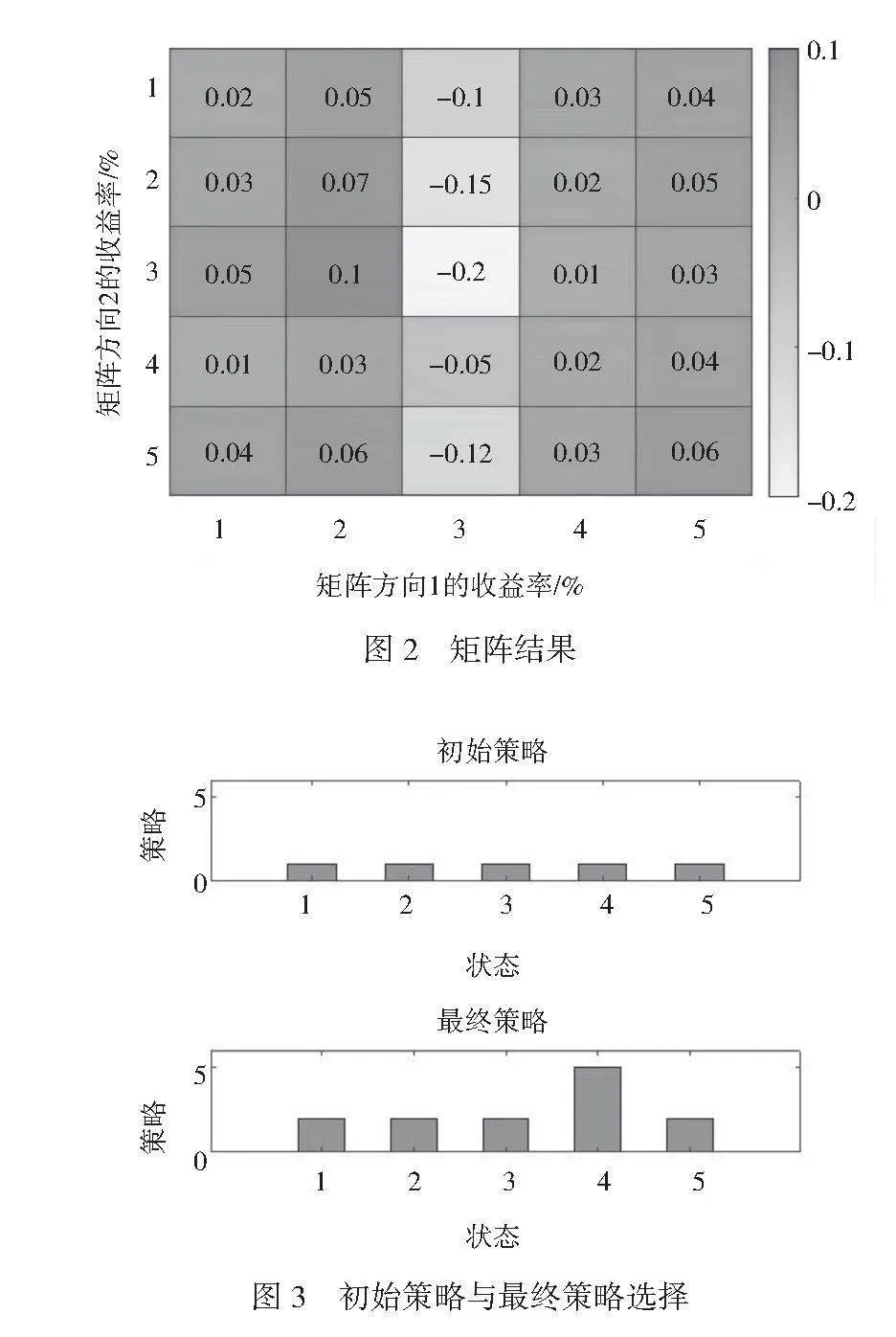
整理其在兩個不同矩陣方向上的結果如圖2所示。由圖2可知，關于建設成本（序號3），當評估項目所在地總體建設費用時，就需要選擇當前資金儲備水平下可投資規模，并描述由融資費率變化等因素引起的建設活動上所做相應調整，以評估當前構造開銷與未來預期回報間關系。在狀態3中，觀察到針對2個矩陣方向的提升導致收益率明顯下降。這一現象意味在考慮了政策支持、稅收環境、建設成本、風能資源和并網潛力等指標后，采取特定動作可能會帶來較低的經濟回報或效益。綜合考慮這些因素將有助于更好地制定長期規劃，并通過馬爾科夫決策過程框架優化決策，以最大化效益。最終，整理政策決策結果如圖3所示。

在保持初始策略穩定的情況下，可以觀察到狀態4顯著上升。這種趨勢似乎暗示一種特定需求：即使其他條件發生變化，系統在特定環境中（即保持初始策略不變）需要被引導至另一個特定狀態（狀態4），以實現更高效益或達成其他目標。

3 結語

在風電項目投資中，利用馬爾科夫決策過程理論構建的模型為決策者提供了重要參考。通過引入多方面因素和動態環境下的不確定性，這種方法有助于優化資源配置、降低風險并提高回報。前述研究表明，在風電領域應用馬爾科夫鏈技術可以有效改進功率預測精度、管理日前不確定性，并實現可靠時間序列分析等目標。

模型構建闡釋了如何將狀態空間、動作空間、轉移概率和回報函數結合起來，以更好地描述系統中各個變量之間的關系，并制定相應最優化戰略。循環迭代的過程展示出值函數平滑上升趨勢，突顯了算法在對最佳操作選擇及環境特性理解上取得良好效果。

結果分析則呈現出針對不同指標進行決策時帶來的收益率變化情形。其中，在保持初始穩定策略下觀察到狀態4大幅上升可能意味特殊需求：即使其他條件發生變化，系統需要被引導至另一個特定狀態，以實現更高效益目標。

參考文獻

[1]翟保豫，張龍，徐志，等.基于WRF模式和風速誤差修正的中期風電功率預測方法[J].智慧電力，2023，51（7）：31-38.

[2]張彬橋，葛蘇葉，李成.基于Copula函數的馬爾科夫鏈風速預測模型[J].智慧電力，2021，49（11）：24-30，37.

[3]楊輝明，雷勇.基于改進馬爾科夫鏈的風電日前不確定性建模方法[J].南方電網技術，2021，15（7）：54-60.

[4]劉大貴，王維慶，張慧娥，等.馬爾科夫修正的組合模型在新疆風電中長期可用電量預測中的應用[J].電網技術，2020，44（9）：3290-3297.

[5]樊盼盼，袁逸萍，孫文磊，等.融合多時段SCADA數據的風電機組風險態勢預測[J].計算機集成制造系統，2021，27（7）：1993-2004.

[6]張文秀，韓肖清，宋述勇，等.計及源-網-荷不確定性因素的馬爾科夫鏈風電并網系統運行可靠性評估[J].電網技術，2018，42（3）：762-771.