軋機垂扭耦合振動控制模型的建立與優化

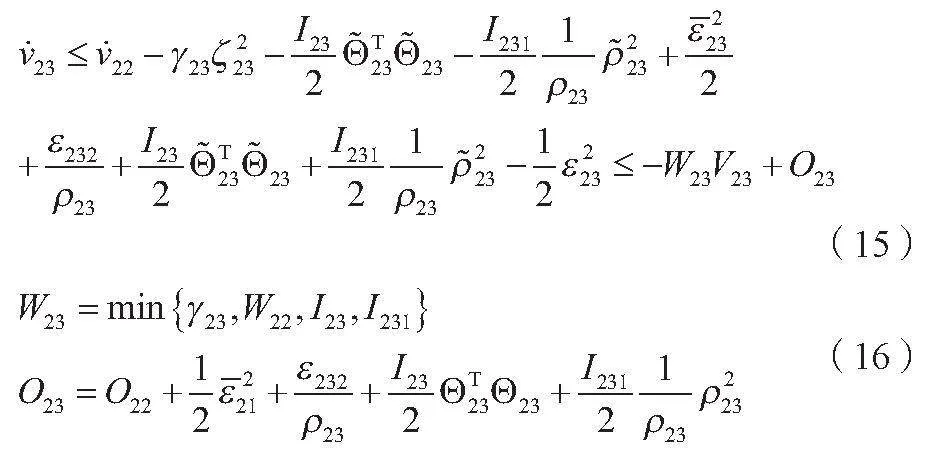
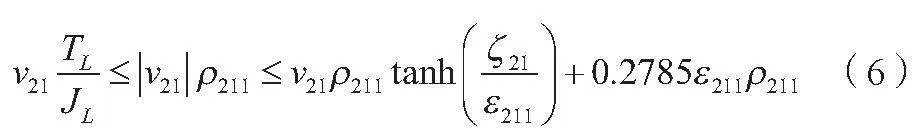
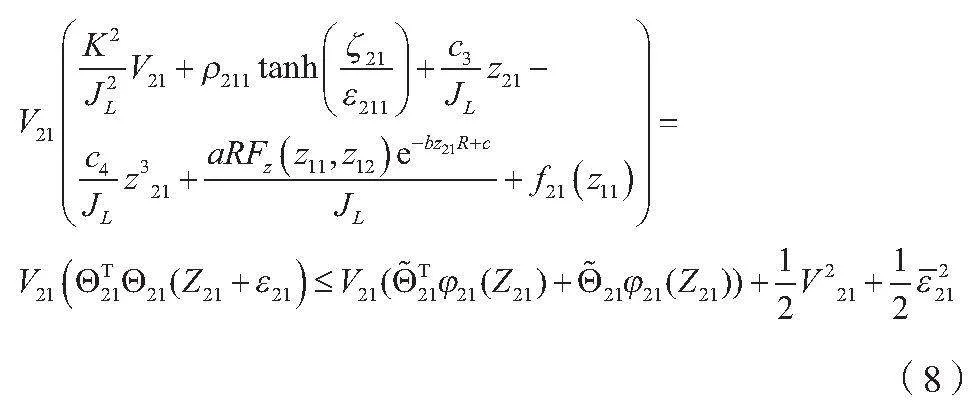
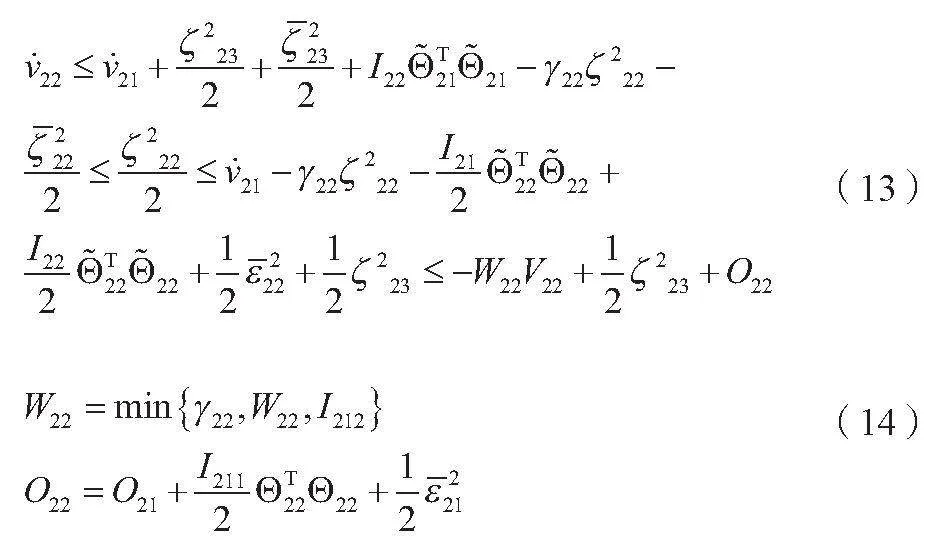
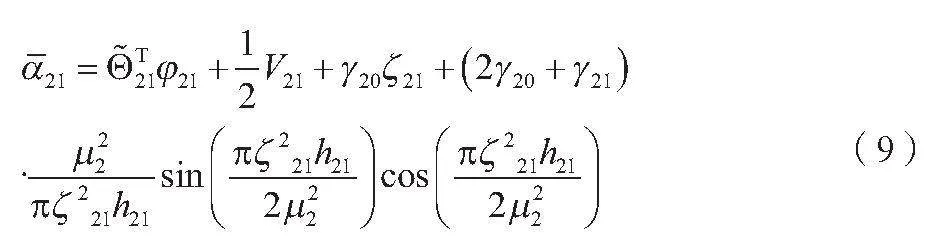
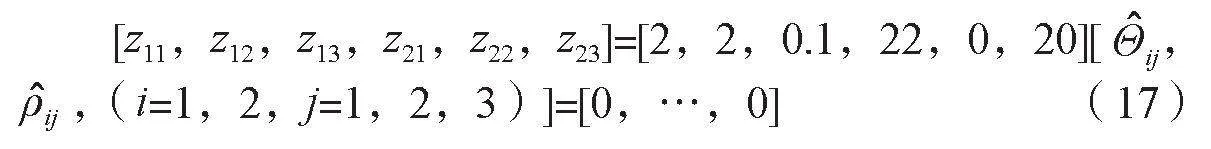
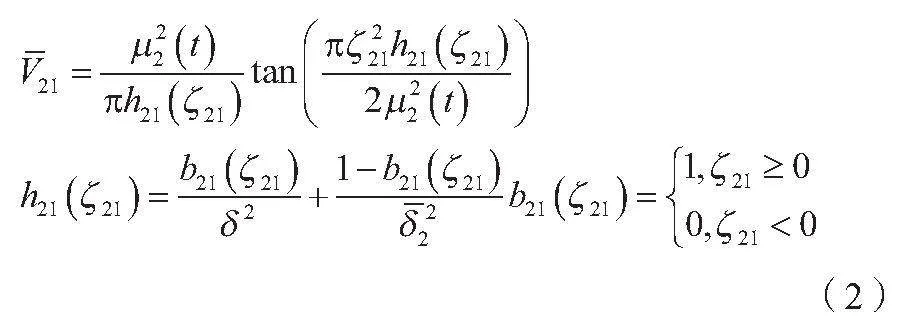
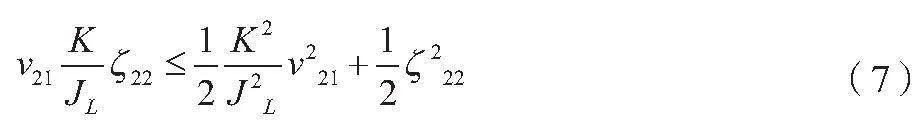
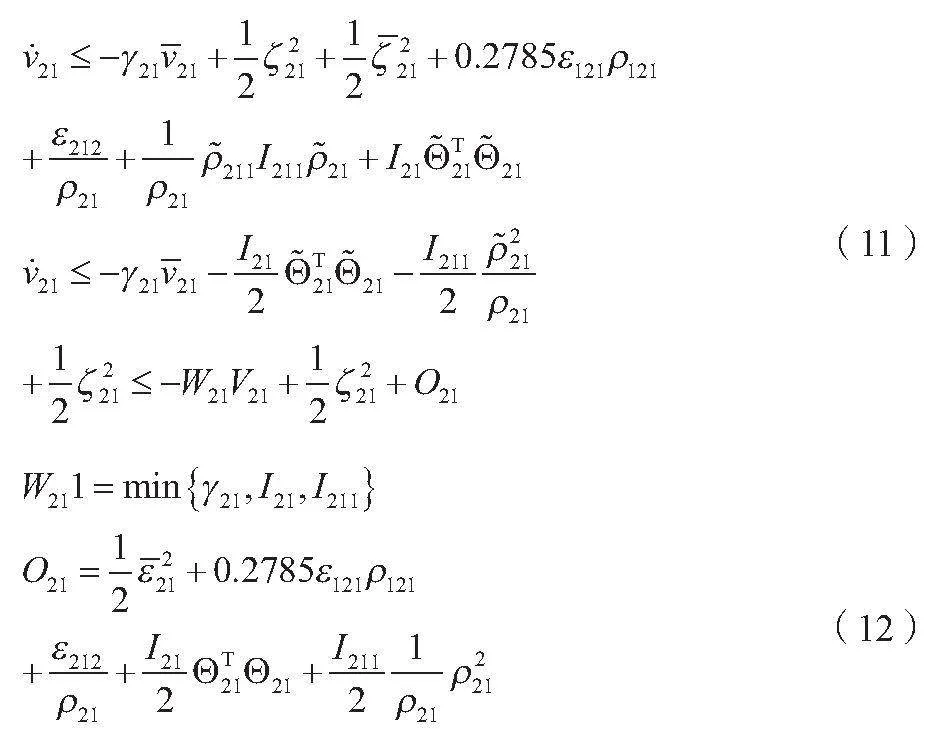
摘 要：本文針對軋機垂扭耦合振動問題，建立了相應的控制模型，并提出了一種優化方法。首先，分析軋機系統的動力學特性，建立垂扭耦合振動的數學模型。其次，基于該模型提出一種基于控制理論的優化方法，以有效控制軋機振動。最后，通過仿真試驗驗證所提方法的有效性和優越性。本文算法引入了輸出性能約束，建立了合理的控制策略，能夠使系統的狀態變量始終保持在有界范圍內，從而提高了系統的穩定性。

關鍵詞：軋機；耦合振動；控制模型

中圖分類號：TG 333" " 文獻標志碼：A

軋機是一種重要的金屬加工設備，廣泛應用于鋼鐵、有色金屬等行業。但是軋機結構復雜并具有一定的工作特性，經常會出現垂扭耦合振動問題，嚴重影響了軋機的工作效率和產品質量[1]。因此，對軋機垂扭耦合振動進行控制和優化具有重要的理論和實際意義。本文旨在建立相應的控制模型和優化方法，提供一種有效的解決方案。

1 軋機垂扭耦合振動控制模型的建立

1.1 整體設計思路

本文針對扭振系統，設計了一個扭振控制器來抑制扭轉振動。該控制器可測量扭轉振動的反饋信號，并結合系統模型和控制算法生成相應的控制信號來抑制扭轉振動[2]。并優化控制器參數和調節算法，對扭轉振動進行有效控制。

1.2 具體設計算法

本文建立了軋機主傳動扭振系統的數學模型，該系統包括軋機主傳動系統和扭振系統，本文主要探討扭振系統。扭振系統由軋機輥和軋機輥間的彈簧、阻尼器組成。反步坐標變換是一種將系統的輸入和輸出變量進行轉換的方法，能更好地描述系統的動態特性[3]。本文將扭振系統的扭轉角度和扭轉角速度作為反步坐標。針對軋機主傳動扭振系統，引入反步坐標變換，如公式（1）所示。

式中：z21為電機轉動角速度；z22為電機轉動角度-電機轉動角速度；z23為電機轉動角度；α21、α22分別為虛擬控制器；ζ21、ζ22和ζ23分別為輸出變量。

在軋機垂扭耦合振動控制模型的建立中，本文引入正切障礙李雅普諾夫函數，將其作為描述系統穩定性的函數，定義一個障礙函數來限制系統的輸出變量可以有效控制系統的性能。在耦合垂振問題中，本文構造了一個非對稱的正切障礙李雅普諾夫函數來限制輸出變量的性能。非對稱是指障礙函數的上界和下界不對稱，這樣可以使系統對輸出變量的上界和下界具有不同響應，從而更好地控制系統的振動行為。當建立軋機垂扭耦合振動控制模型時，本文將正切障礙李雅普諾夫函數引入系統的控制策略中。合理選擇障礙函數的形式和參數可以限制系統輸出變量在一定范圍內波動，從而有效控制系統的振動幅度和穩定性。特別是在耦合振動問題中，正切障礙李雅普諾夫函數的非對稱性可以更好地適應系統的復雜性，提高系統的控制性能和穩定性[4]。為了限制輸出變量ζ21的性能，需要構造非對稱的正切障礙李雅普諾夫函數，如公式（2）所示。

1.2.1 構建第一部分的李雅普諾夫函數

為了使輸出變量ζ21趨于穩定，構建第一部分的李雅普諾夫函數，分別如公式（3）、公式（4）所示。

在軋制過程中，軋機會施加一定壓力和扭矩，將金屬坯料壓制成所需形狀和尺寸。不同厚度和規格的產品需要不同的軋制參數和工藝調整，這就需要在切換不同產品過程中進行相應調整和適應[5]。然而，在切換過程中，產品的厚度和規格的變化會導致軋機主傳動系統的負載轉矩發生變化。這種變化是突變的、不確定的，甚至會產生沖擊和振動。這樣的不確定干擾會對軋機的穩定性和軋制質量產生負面影響，因此負載轉矩表示為公式（5）。

TL=TL1+TLD " " " " " " " " " " " " （5）

式中：TL1為穩定軋制時的負載轉矩；TLD為軋制過程存在干擾導致的干擾轉矩。

公式（5）的引理如公式（6）所示。

式中：v21為控制輸入或控制信號的增益；ρ211為物理參數或系統參數；tanh為雙曲正切函數；ε211為小的正數。

根據定義的狀態變換z22=ζ22+α21，由楊氏不等式可得公式（7）。

楊氏不等式的意義在于它給出了組合數的一個上界估計。利用RBF神經網絡來逼近未知的非線性函數，將輸入值輸入網絡中，經過隱藏層計算和輸出層計算得到網絡的輸出值。這個輸出值就是對未知函數在該輸入值下的逼近值。利用RBF神經網絡來逼近未知的非線性函數，如公式（8）所示。

式中：K為系統的增益系數；JL為系統的轉動慣量；c3、c4分別為常數系數；aRFz為RBF神經網絡的權重；φ21（Z21）為RBF神經網絡的基函數。

PID控制器是最常用的虛擬控制器之一，包括比例、積分和微分3個控制分量。調節這些分量的參數，可實現系統的穩定性和響應速度的折衷。PID控制器適用于許多線性和部分非線性系統。模型參考自適應控制（MRAC）利用在線辨識系統模型，并根據模型誤差來調整控制器參數，從而實現對系統的自適應控制。MRAC適用于系統參數變化較快或不確定的情況。本文選取的虛擬控制器和自適應律分別如公式（9）、公式（10）所示。

將公式（9）帶入公式（10）可得公式（11）、公式（12）。

1.2.2 構建第二部分的李雅普諾夫函數

計算方式與第1.2.1節的第一部分相似，得到第二部分的李雅普諾夫函數，分別如公式（13）所示。

1.2.3 構建第三部分的李雅普諾夫函數

計算方式與第1.2.1節的第一部分相似，得到第三部分的李雅普諾夫函數，分別如公式（15）、公式（16）所示。

2 模型仿真驗證

2.1 仿真設置

本文選取650mm軋機為仿真對象，軋機機電液垂扭耦合系統的仿真參數如下：m1為（8.9357×104）kg，kv為（1.25×10-4）m/v，k11為（7.2×1010）N/m，βe為（7×108）Pa，c11為（1.2×106）（N·s）/m，V為0.0732m3，Ps為（2×107）Pa，

Jm為1552kg·m2，P2為（1×106）Pa，JL為1542kg·m2，A1為（1.9635×10-1）m2，A2為（3.015×10-2）m2，TL1為14500N·m，Ct為（5×10-16）N·m，TLD為（2190×sinπt）N·m，Cd為0.62，R為0.4，w為0.119，c1為0.2，c2為0.1，c3為0.1，c4為0.2，a為0.13，B為0.002，c為0.2。

軋機垂扭耦合系統狀態初始值選取如公式（17）所示。

2.2 仿真結果

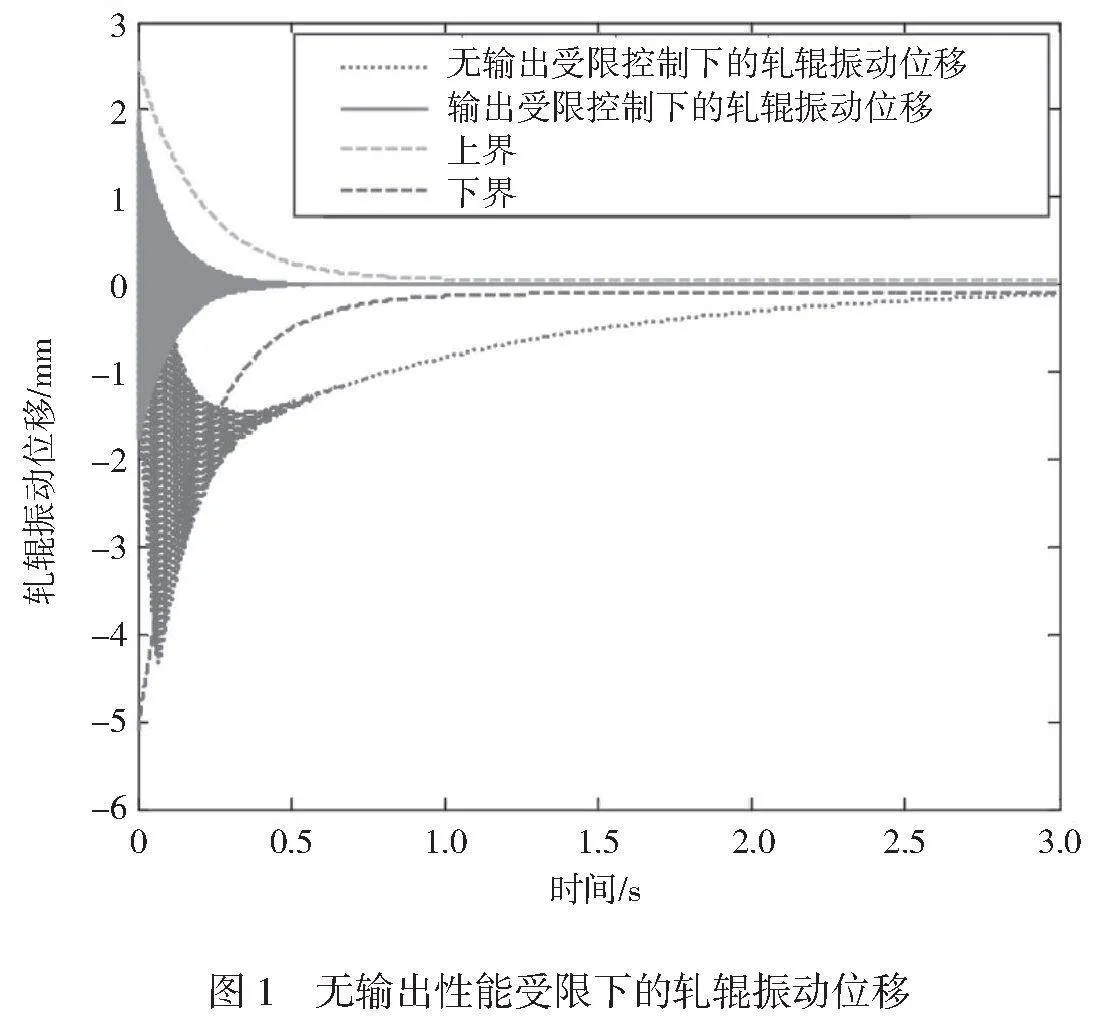
利用本文提出的控制算法，軋輥振動位移的衰減速度得到了顯著提高。傳統的無輸出性能約束控制方法無法有效抑制振動的衰減速度，導致系統的響應時間較長。而本文算法能夠合理控制策略和參數調節，快速減少振動位移，使系統的衰減速度更快，從而提高了系統的動態性能。在穩態誤差方面，本文的控制算法也取得了良好效果。傳統的無輸出性能約束控制方法無法消除系統的穩態誤差，導致系統無法達到期望的穩定狀態。而本文算法引入額輸出性能約束，能夠有效減少穩態誤差，使系統能夠達到期望的穩定狀態。超調量是衡量系統控制性能的重要指標之一。傳統的無輸出性能約束控制方法在控制過程中存在較大超調量，導致系統的響應過程不夠平滑。而本文算法能夠優化控制策略和參數調節，有效減少超調量，使系統的響應過程更平滑、穩定。

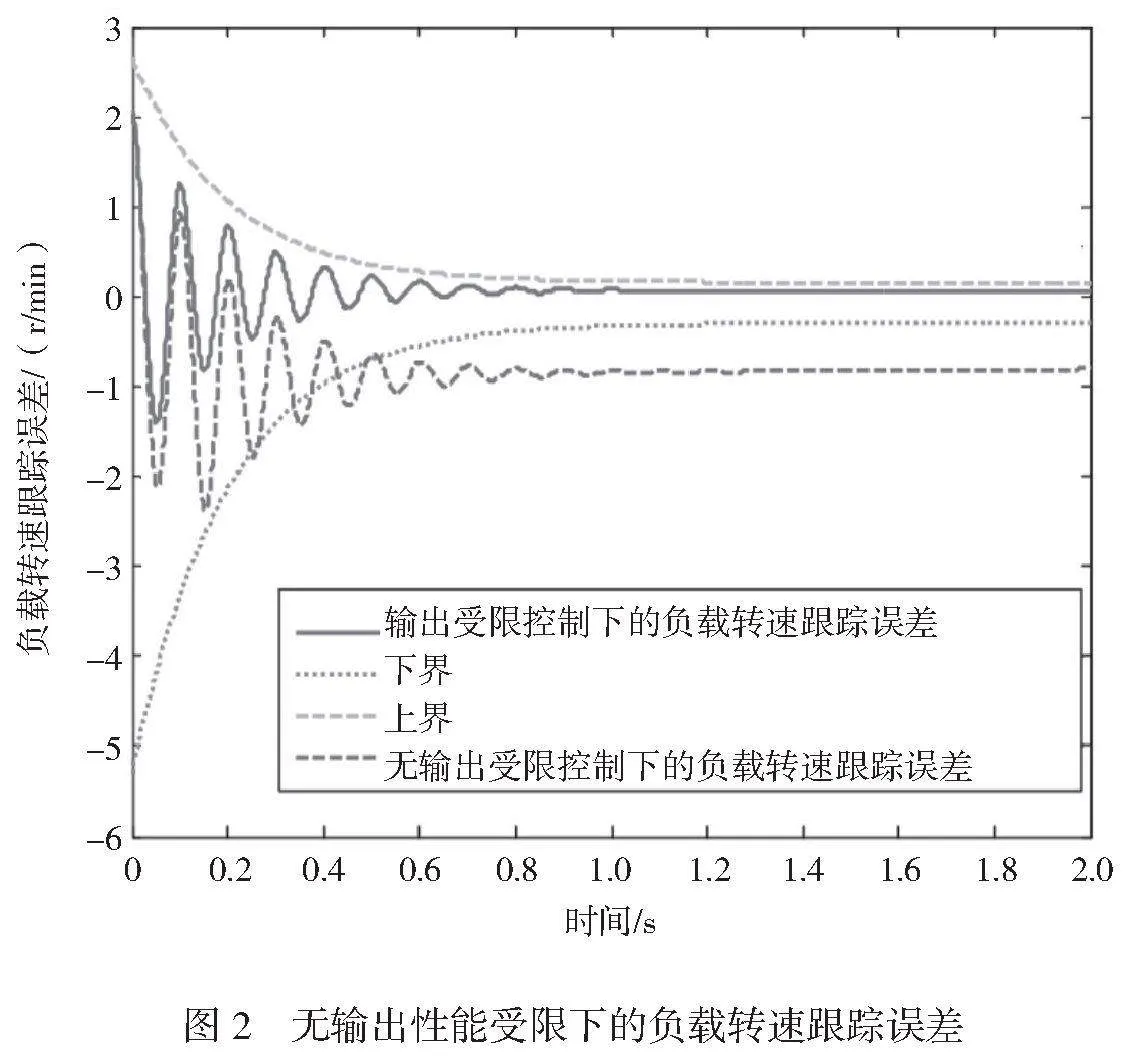
無輸出性能受限下的軋輥振動位移、無輸出性能受限下的負載轉速跟蹤誤差分別如圖1、圖2所示。利用本文提出的控制算法，負載轉速的跟蹤誤差趨于穩定。傳統的無輸出性能約束控制方法無法有效控制負載轉速的誤差，導致系統的跟蹤性能較差。而本文算法引入了輸出性能約束和合理的控制策略，能夠快速減少跟蹤誤差，使其穩定在規定的上、下界內，從而提高了系統的動態性能。在穩態性能方面，本文的控制算法也取得了良好效果。傳統的無輸出性能約束控制方法無法嚴格限制負載轉速的跟蹤誤差，導致系統無法達到期望的穩定狀態。而本文算法優化了控制策略和參數調節，能夠將跟蹤誤差嚴格限制在規定的上、下界內，使系統能夠更好地達到期望的穩定狀態。

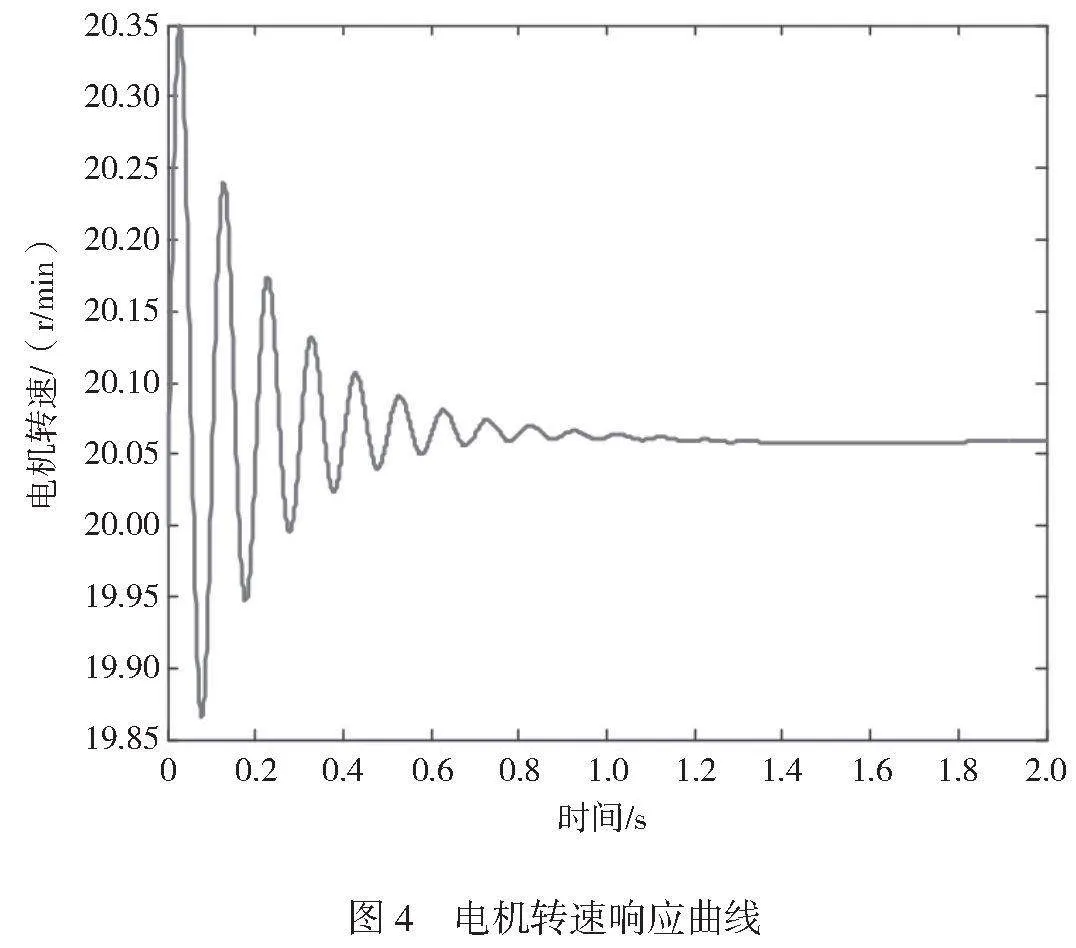
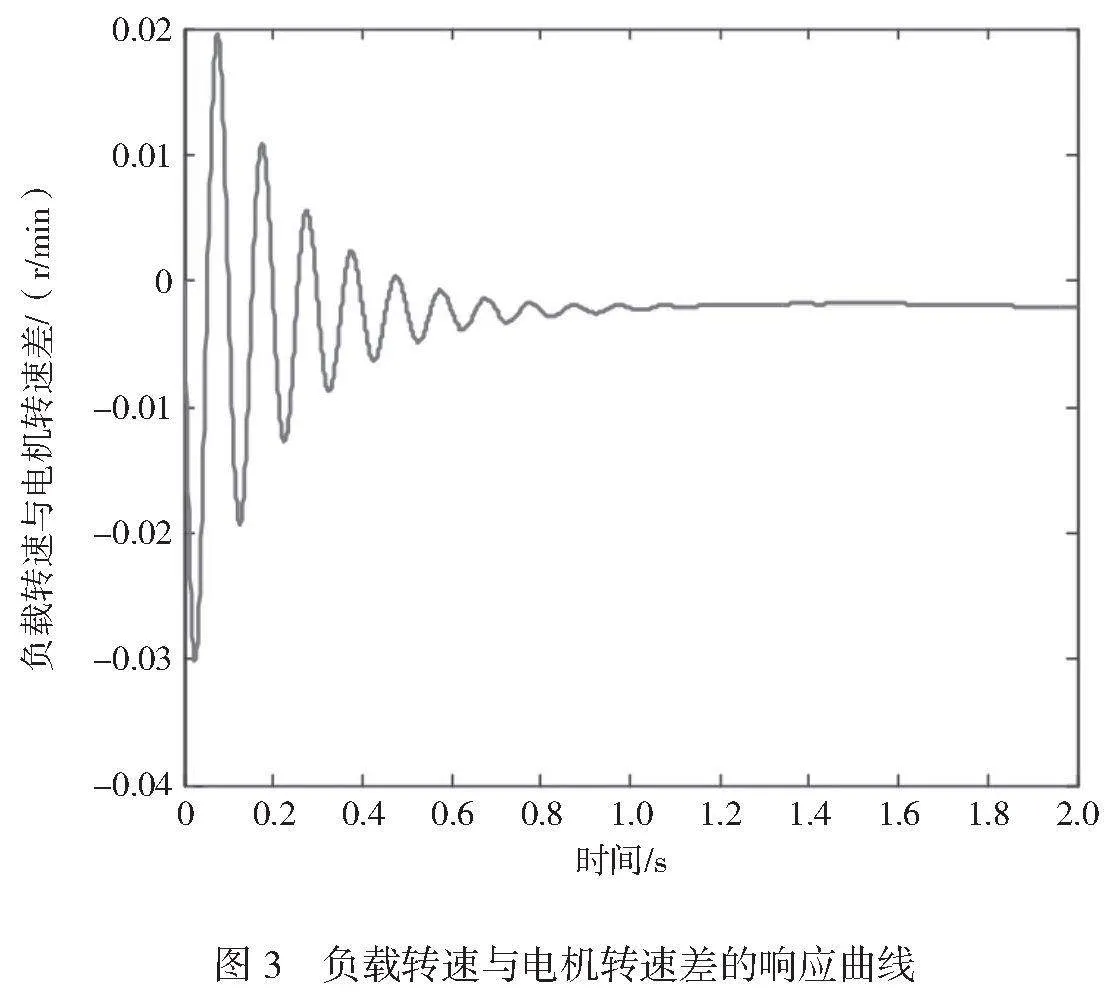
負載轉速與電機轉速差的響應曲線和電機轉速響應曲線分別如圖3、圖4所示。傳統的無輸出性能約束控制方法無法有效控制振動速度，導致系統的振動速度波動較大。而本文算法引入了輸出性能約束和合理的控制策略，能夠快速減少振動速度的波動，并使其趨于穩定。傳統的無輸出性能約束控制方法無法嚴格限制液壓缸無桿腔工作壓力的波動，導致系統的壓力不穩定。而本文算法優化了控制策略和參數調節，能夠有效控制液壓缸無桿腔工作壓力的波動。傳統的無輸出性能約束控制方法無法保證系統的狀態變量不超出規定范圍，影響系統的穩定性。而本文算法引入了輸出性能約束和合理的控制策略，能夠將系統的狀態變量始終保持在有界范圍內，從而提高了系統的穩定性。

3 結語

本文對軋機垂扭耦合振動問題進行建模和優化，提出了一種基于控制理論的優化方法仿真試驗表明，該方法能夠有效控制軋機的振動，提高軋機的工作效率和產品質量。本文的研究成果對軋機行業的發展具有重要意義，也為其他領域的振動控制問題提供了借鑒和參考。未來的研究進一步探索更高效的優化方法，以進一步提升軋機垂扭耦合振動控制的效果和性能。

參考文獻

[1]侯東曉，陳善平，方成，等.萬向接軸附加動態彎矩下板帶軋機垂扭耦合振動特性研究[J].振動與沖擊，2022，41（19）：48-54，63.

[2]李苗苗，王衛，李英民.錨桿-圍巖結構的耦合振動和減振[J].土木與環境工程學報（中英文），2024（2）：51-59.

[3]張宗素，王婷，譚帥，等.基于Galerkin截斷的薄膜-床面耦合振動響應分析[J].噪聲與振動控制，2024，44（2）：22-26.

[4]王少欽，馬仕杰，郭明浩，等.風荷載對車橋耦合振動及行車舒適性影響[J].公路交通科技，2024，41（4）：51-64.

[5]吳志淵，閆寒，吳林潮，等.旋轉裂紋葉片-彈性輪盤耦合系統振動特性[J].航空學報，2022，43（9）：101-114.