新能源項(xiàng)目智能監(jiān)控系統(tǒng)在后期運(yùn)維中的應(yīng)用

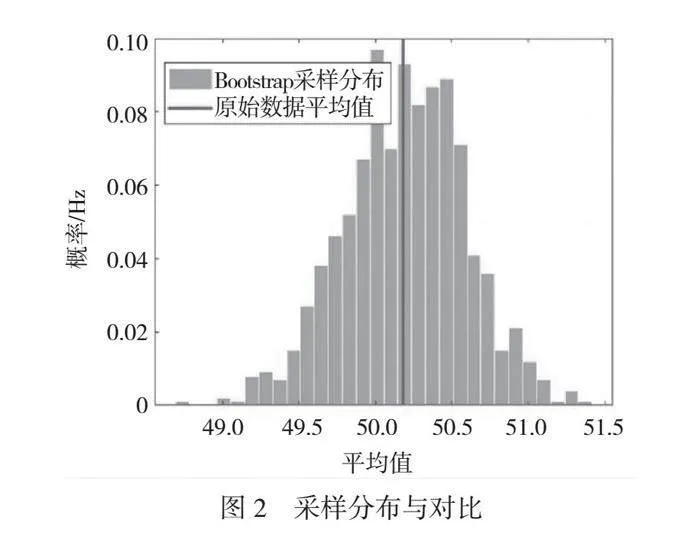
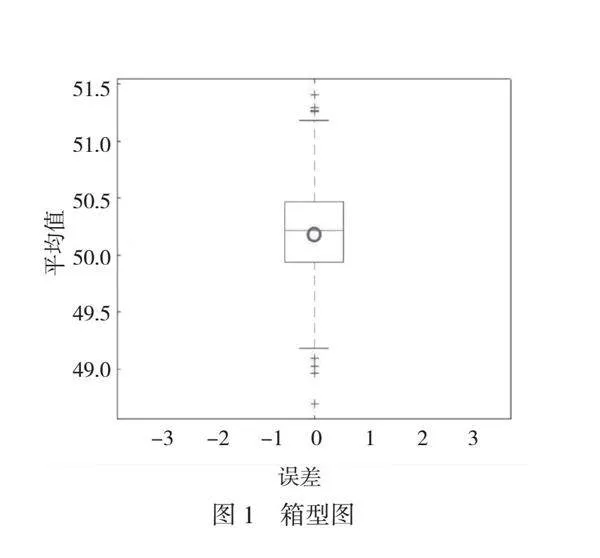
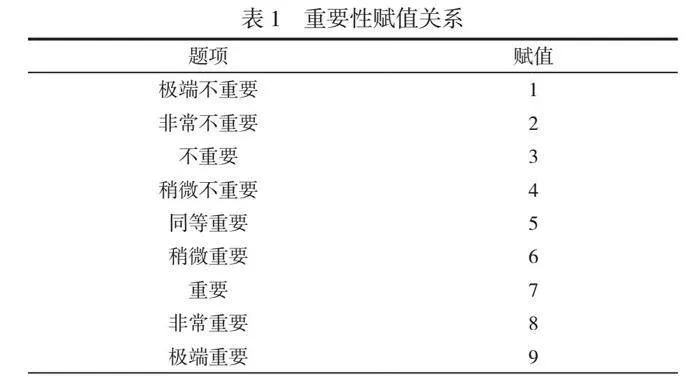
摘 要：本研究的目標(biāo)是利用層次分析法（Analytic Hierarchy Process，AHP）和熵值法構(gòu)建一個(gè)全面的評價(jià)體系，以評估新能源項(xiàng)目智能監(jiān)控系統(tǒng)在后期運(yùn)維中的效益。考慮在實(shí)際運(yùn)營過程中數(shù)據(jù)的稀缺性，在評估過程中引入Bootstrap方法。Bootstrap方法利用重復(fù)抽樣構(gòu)建多個(gè)虛擬樣本，優(yōu)化模型的預(yù)測性能。為評估監(jiān)控系統(tǒng)的效益，進(jìn)行Bootstrap采樣分析，將采樣分布結(jié)果與原始數(shù)據(jù)進(jìn)行對比。這種方法能夠更全面了解系統(tǒng)性能，準(zhǔn)確評估后期運(yùn)維效益。本研究旨在為新能源項(xiàng)目的智能監(jiān)控系統(tǒng)提供科學(xué)、可靠的評估框架，優(yōu)化運(yùn)營系統(tǒng)，提升可持續(xù)性。

關(guān)鍵詞：新能源項(xiàng)目；智能監(jiān)控系統(tǒng)；效益評估；Bootstrap方法

中圖分類號：X 924 " " " " 文獻(xiàn)標(biāo)志碼：A

在新能源領(lǐng)域，智能監(jiān)控系統(tǒng)在提高系統(tǒng)性能、降低運(yùn)維成本方面起到了關(guān)鍵作用，因此備受關(guān)注。成建國等[1]（2023）深入研究了深圳城際動車組智能化需求以及頂層指標(biāo)建議方案，提出了創(chuàng)新的智能化方案，為城際動車組運(yùn)營提供了新思路。樊任璐[2]（2023）研究上海軌道交通1號線空調(diào)智能運(yùn)維系統(tǒng)。陳澤濤等[3]（2022）研究配電房安全智能監(jiān)控平臺接地刀閘狀態(tài)位監(jiān)控方法。鐘怡然等[4]（2022）從現(xiàn)有智能監(jiān)控系統(tǒng)中發(fā)展了三維建模技術(shù)并將其應(yīng)用于安防領(lǐng)域。談?wù)鸬萚5]

（2022）研究水利工程智能運(yùn)維全鏈路監(jiān)控系統(tǒng)。王學(xué)文等[6]（2022）研究AR/VR融合驅(qū)動的綜采工作面智能監(jiān)控關(guān)鍵技術(shù)。劉海濱等[7]（2018）研究水電站智能監(jiān)控服務(wù)支持系統(tǒng)，為水電站提供全面的監(jiān)控服務(wù)。于闖等[8]（2018）研究了動車組轉(zhuǎn)向架智能監(jiān)控分析平臺。……