基于優化神經網絡的二自由度機械臂軌跡跟蹤

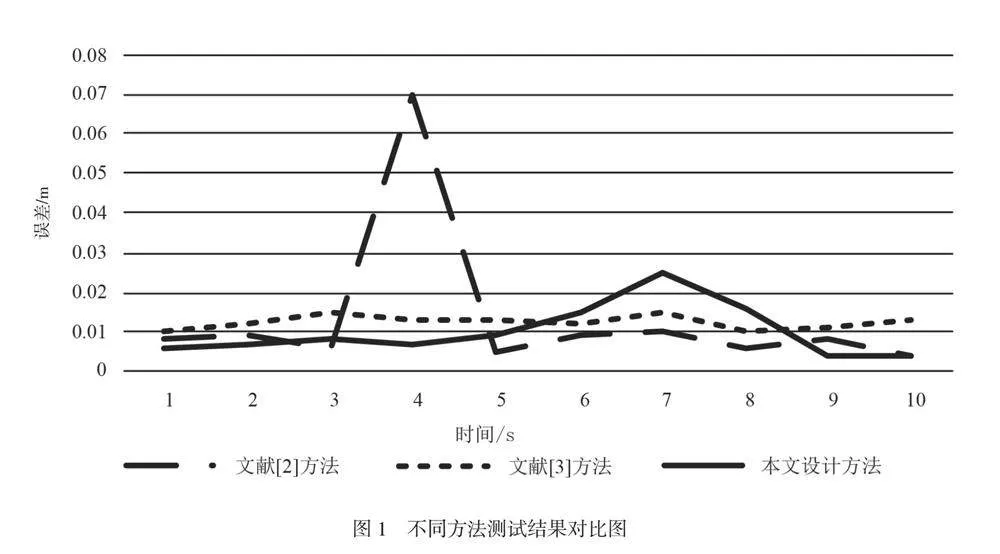
摘 要：針對二自由度機械臂的軌跡跟蹤問題，本文提出基于改進微分進化優化神經網絡的二自由度機械臂軌跡跟蹤方法。分析其動力學方程，從周期性振動、瞬態響應和穩定運動狀態3個角度探討了二自由度機械臂的動態行為表現形式，將軌跡跟蹤轉化為求解二自由度機械臂非線性微分方程。采用約束處理機制改進基本微分進化算法，利用多層感知器（Multilayer Perceptron，MLP）結構的神經網絡跟蹤二自由度機械臂軌跡。測試結果表明，跟蹤誤差始終保持在0.010 m以內，最大值為0.010 m，最小值為0.003 m，與對照組相比具有明顯優勢。

關鍵詞：改進微分進化；優化神經網絡；二自由度機械臂；軌跡跟蹤；動力學方程；動態行為表現形式；約束處理機制；MLP結構

中圖分類號：G 254 " " " " " 文獻標志碼：A

二自由度機械臂是一種有2個旋轉關節的機器人，運行特性獨特，其運動學模型相對簡單，由于關節旋轉，其運動學方程是非線性的[1]，對機器人進行精確控制和軌跡跟蹤的難度較高，因此，要完成特定的軌跡（即機器人末端執行器的路徑和速度），須對二自由度機械臂進行精確的軌跡規劃。為了進行精確的軌跡跟蹤，需要高精度的控制器。在實際應用中，除了機械臂自身的因素外，還要考慮環境因素的影響，須結合優化算法、先進的控制策略和傳感器技術，對二自由度機械臂進行精確控制和軌跡跟蹤，還須不斷調整和優化控制策略，以適應各種復雜的工作環境，滿足不同的任務需求。李東民等 [2]提出以模糊滑模反步控制為基礎的機械臂軌跡跟蹤方法， 盧紫超等[3]提出以干擾觀測器為基礎的機械臂軌跡跟蹤方法，它們都在一定程度上提高了跟蹤精度，但是在二自由度機械臂方面存在局限性。……