分布式電源與配電自動化終端協同規劃研究

摘 要：在分布式電源并網發電的背景下，為了提高配電網規劃的合理性，同時降低總體的規劃運營成本，本文提出了分布式電源與配電自動化終端協同規劃模型。該模型由2個部分組成。上層規劃模型用于確定分布式電源在配電網中的最佳接入位置和容量，其目標函數為綜合運行成本最低，約束條件包括孤島約束、潮流約束和容量約束等。下層規劃模型根據分布式電源的規劃方案，進一步確定配電自動化終端的安裝位置，其目標函數為停電損失和終端成本最低，約束條件為系統可靠性。完成建模后，利用仿真軟件對IEEE 33節點進行規劃。結果顯示，其規劃成果的總成本和可靠性計算結果均優于對照組，驗證了規劃模型的實用性。

關鍵詞：分布式電源；自動化終端；協同規劃

中圖分類號：TM 715" " " 文獻標志碼：A

配電自動化終端能夠遙測、遙控配電網中的一次設備，是電網智能化的重要基礎。隨著新能源并網發電規模持續擴大，分布式電源的接入數量和總容量呈快速上升趨勢。因此，在規劃配電網過程中應強化分布式電源和配電自動化終端的協同性，通過科學設計明確各類設備的接入位置，從而控制安裝和運營成本。本文以綜合運行成本、停電損失和配電自動化成本最低為目標，提出了協同規劃模型，該模型能夠提升配電網規劃質量，并提高系統的可靠性。

1 分布式電源與配電自動化終端協同規劃方法設計

1.1 分布式電源與配電自動化終端協同規劃模型

1.1.1 協同規劃模型技術方案設計

1.1.1.1 協同規劃的目標

分布式電源和配電自動化終端是配電網的重要組成部分，分布式電源包括光伏發電設備、風力機組和儲能設備等。配電自動化終端為配電網的二次設備，用于遠程測量、通信和控制，監控對象為包括分布式電源在內的各類一次設備[1]。

配電自動化終端能夠提高配電網的可靠性，并能在配電網出現故障情況下，利用遠程控制快速形成孤島，提高非故障區域的供電可靠性。協同規劃的目標是合理設置分布式電源、配電自動化終端的位置，從而提高供電可靠性并降低綜合運行成本。

1.1.1.2 基于協同規劃的雙層模型

本文設計的協同規劃模型分為上、下2層。上層規劃模型的控制目標為綜合運行成本最低，下層規劃模型的控制目標為停電損失和配電自動化終端投資運行成本最低，整體的技術方案如圖1所示。上層規劃模型的主要作用是確定分布式電源的接入位置和容量，下層規劃模型以上層規劃模型生成的分布式電源規劃方案為基礎，進一步明確配電自動化終端和分段開關的配置方案。2個階段的目標函數均建立在成本控制的基礎上，并且上、下層規劃模型的輸出結果能夠相互作用，實現了配電自動化終端與分布式電源的協同規劃[2]。

1.1.2 上層規劃模型的目標函數和約束條件

1.1.2.1 上層規劃模型的目標函數

上層規劃模型的目標函數以配電網綜合運行成本最低為控制目標。綜合運行成本具有多個分項，包括線損、向上級網絡的購電費用和分布式電源的投資運行成本等。

1.1.2.2 上層規劃模型的約束條件

根據技術方案，上層規劃模型具有多種約束條件，例如潮流約束、孤島約束、電壓約束以及分布式電源安裝容量約束等。

分布式電源安裝容量的約束條件如公式（1）所示。

（1）

式中：N為安裝分布式電源的節點總數量；Pdg，i為第i個節點的分布式電源安裝容量；Pload為電網中有功負荷的總和；δ為分布式電源在配電網中的滲透率；Pi，max為配電中節點i能夠安裝的分布式電源最大容量。

例如，在某配電網中，需要計算每個節點可以安裝的分布式電源的最大容量，以滿足系統穩定性和負載需求的約束條件。該配電網總有功負荷為5000kW，滲透率為20%，節點1能夠安裝的分布式電源最大容量為1000kW，節點2能夠安裝的分布式電源最大容量為800kW。則節點1的Pdg，1≤0.2×5000=1000kW，節點2的Pdg，2≤0.2×5000=1000kW，根據上述計算，分布式電源的安裝容量應滿足以下約束條件：節點1的分布式電源安裝容量不超過1000kW，節點2的分布式電源安裝容量不超過800kW。

孤島劃分是提高配電網可靠性的重要技術措施。當配電網中的局部區域出現故障時，采用孤島劃分對其進行隔離。該技術能夠降低故障區域對非故障區域的干擾，從而保證其他區域能夠正常供電[3]。因此，在分布式電源與配電自動化終端協同規劃中，需要設置孤島約束條件，如公式（2）所示。

（2）

式中：Y為孤島區域中配電自動化終端的集合；PFDi為孤島中第i個分布式電源的發電量；PLj為孤島區域中第j個負荷節點的有功功率；Z為孤島區域中負荷節點的集合；Ploss1為孤島區域內的線損。

對于電壓約束，要求系統中任意節點的電壓幅值不得超過最大、最小電壓閾值，即Umin≤Ui≤Umax。Ui為系統中節點i的電壓幅值，Umin為系統電壓幅值下限閾值，Umax為系統電壓幅值上限閾值[4]。

在某配電網中，孤島區域中的有功功率為3000kW，孤島區域中的線損為200kW，設孤島區域內分布式電源的發電量為PFDi，最小電壓閾值為0.95，最大電壓閾值為1.05。根據上述公式，可得該電網孤島約束條件為Pload=3000+200=3200kW，根據給出的滲透率計算分布式電源的安裝容量，即Pdg，i≤δ?Pload，假設δ=0.3，則可得Pdg，i=0.3?3200=960kW，根據上述計算和約束條件，孤島模式下每個節點的分布式電源安裝容量應滿足以下2個條件。1）分布式電源不超過960kW，以保證孤島區域能夠在故障情況下穩定運行。2）保證系統中任意節點的電壓在（0.95～1.05）p.u.，以維持電網的穩定性和正常運行。

1.1.3 下層規劃模型目標函數及其約束條件

下層規劃模型的目標函數包括2項成本因素，下層規劃模型目標函數的約束條件為配電網的可靠性。當評估系統的可靠性時，可采用遞歸搜索算法，該方法采用遍歷的方式計算配電網中每條線路的停電可能性，進而求出整體可靠性。

1.2 分布式電源與配電自動化終端協同規劃模型求解

1.2.1 上層規劃模型求解方法

上層規劃采用改進的自適應遺傳算法（ImprovedAdaptiveGeneticAlgorithm，IAGA），求解過程如下所示。1）向IAGA算法輸入基本參數，包括配電網的整體結構、分布式電源和種群數量，并且在這一基礎上設置迭代次數。2）對種群中的染色體進行編碼，由于上層模型的優化重點為分布式電源的位置，因此采用相對簡單的整數編碼方式。在編碼集合中，每個元素的位置信息對應一個分布式電源的位置，每個元素的數量信息對應分布式電源的容量。在滿足滲透率約束的前提下，生成染色體種群[5]。3）根據IAGA算法的應用原理對種群進行遺傳迭代運算，并且在該過程中同步完成孤島劃分，確定具體的孤島范圍。完成以上工作后，利用上、下層規劃模型的目標函數計算出相應的函數值。在迭代運算的過程中，以目標函數F1數值最小為目標，求解出種群個體的適應度值和適應度均值。4）對個體適應度值進行排序，逐漸篩選出適應度較好的個體，將這些優良個體作為選擇種群。5）根據IAGA算法進行交叉運算。6）根據IAGA算法進行變異運算，生成新的種群。7）利用約束條件判斷種群是否滿足要求，當種群中的部分個體超過約束條件時，重新生成對應的染色體，直至種群滿足約束條件[6]。8）在每一次迭代運算中，篩選出最優染色體。重復第3～8步，產生分布式電源的最佳位置方案，同時確定每個分布式電源對應的合理安裝容量。

1.2.2 下層模型求解方法

上層規劃模型生成了配電網中分布式電源的最優設計方案，下層規劃模型以分布式電源安裝位置為依據，進一步確定分段開關和配電自動化終端的設計方案，從而實現分布式電源與配電自動化終端協調規劃[7]。下層規劃模型求解同樣采用IAGA算法，其求解流程如圖2所示。

2 分布式電源與配電自動化終端協同規劃方法算例分析

2.1 算例模型和參數

在算例分析階段，本文采用IEEE33節點配電系統。將該系統中的線路設置為LGJ-240，該型線路的阻抗參數取值為（0.107+j0.405）Ω/km，j為虛數單位。在IAGA算法中，將群眾中個體的數量、算法迭代次數分別設置為70、50，交叉概率的取值為[0.6，0.9]，變異概率的取值為[0.05，0.1]。算例模型的其他重要參數見表1。

2.2 仿真結果分析

2.2.1 協同規劃成果示意圖

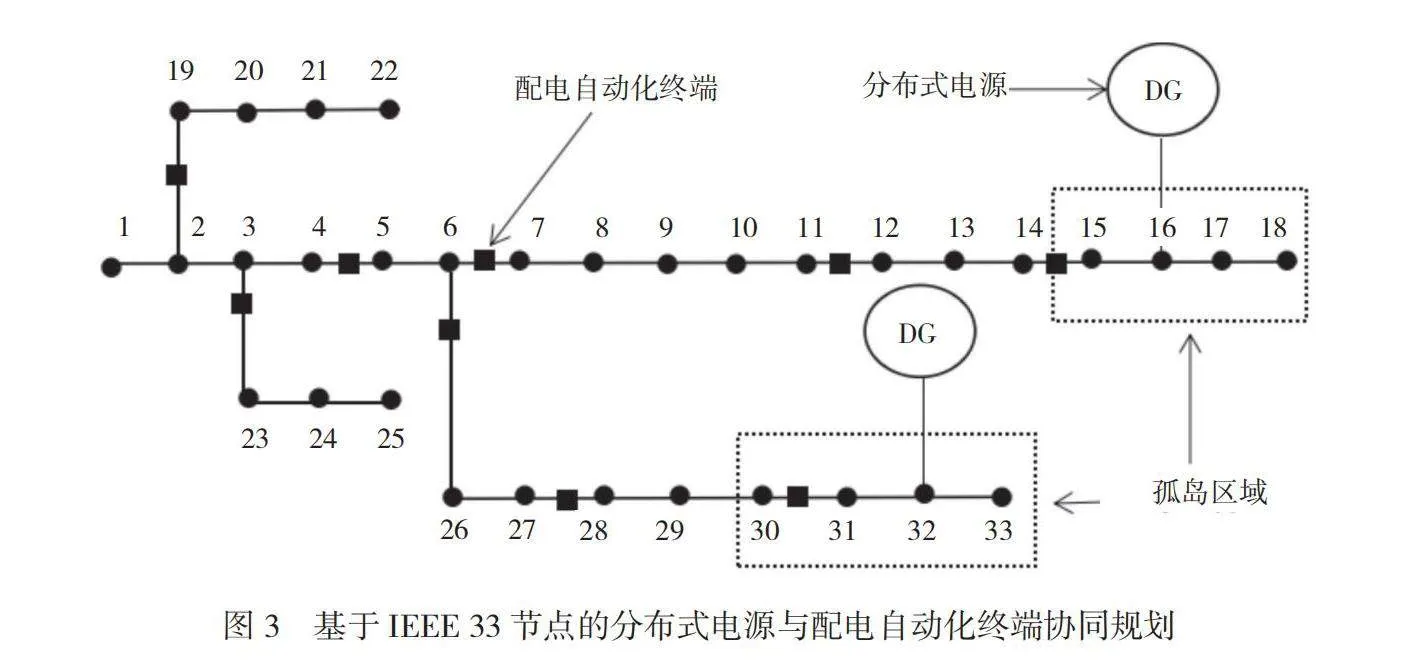
利用本文設計的雙層規劃模型，對IEEE33節點系統進行協同規劃，得到的規劃成果如圖3所示。其中，DG為分布式電源，圓形實心為電力系統的節點，方形實心代表配電自動化終端的安裝位置，虛線框為孤島區域。分布式電源的接入位置為節點16和節點32，對應的安裝容量為400kW、420kW。

2.2.2 基于不同自動化終端的協同規劃成果經濟指標

根據圖3所示的規劃成果計算規劃方案的各項經濟指標，包括綜合運行成本、用戶停電損失費用、配電自動化終端安裝成本和平均供電可用率。由于配電自動化終端包括“二遙”和“三遙”2種類型，其采購成本差異較大，前者為1.9萬元/組，后者為5.5萬元/組。考慮自動化終端的類型，根據不安裝配電自動化終端、全部采用“三遙”終端、“三遙”終端+“二遙”終端3種方案計算以上4項經濟性指標，所得結果見表2。

計算3種方案的各項成本之和，方案1的總成本為831.86+

12.39+4.18=848.43萬元，方案2的總成本為848.38+32.71=881.09萬元，方案3的總成本為833.41+10.56+6.98=850.95萬元。顯然，如果僅考慮總成本最低，那么方案1最佳。平均供電可用率反映了供電系統的可靠性。比較可知，方案3的可靠性最高，其次為方案1。

3 結論

在分布式電源接入量和配電自動化水平持續提高的背景下，配電網規劃工作應該協同設計分布式電源和配電自動化終端，一方面提高系統的可靠性，另一方面控制整體的安裝運行成本，為了節約該問題，本文建立了分布式電源與配電自動化終端協同規劃模型。研究結論如下所示。1）協同規劃模型分為上、下2層模型。上層模型以綜合運行成本最低為目標函數，經過規劃，能夠確定分布式電源在配電網中的接入位置和接入容量，即完成分布式電源規劃。下層規劃模型在分布式電源的規劃基礎上，將停電損失最低和配電自動化終端安裝成本最低作為控制目標，合理規劃出終端和分段開關的安裝位置。2）該模型較復雜，涉及較多的參數和變量。本文在求解模型過程中采用改進的自適應遺傳算法，直至獲得最優解。3）利用IEEE33節點檢驗協同規劃模型的應用效果。結果顯示，該模型能夠有效確定分布式電源、配電自動化終端的接入位置，同時完成孤島劃分。4）在配置自動化終端過程中，為了節約成本，以滿足功能需求為基本前提，可優先采用“二遙”終端。

參考文獻

[1]俞鍵，鄭曄，趙力，等.分布式電源與配電自動化終端的建模分析[J].自動化應用，2022（5）：86-87，91.

[2]張斌，于力，白浩，等.農村有源配電網自動化終端布局規劃方法[J].河北農業大學學報，2020，43（4）：133-140.

[3]厲衛娜，李志杰.含分布式電源的配網自動化終端狀態評價方法[J].信息技術與信息化，2023（12）：135-138.

[4]王璨，馬金輝，王松，等.基于分布式電源的新型配網綜合自動化調度模型[J].微型電腦應用，2024，40（5）：92-95.

[5]徐曉，徐琦睿，賀威，等.基于功率預測的含分布式電源電網自動化無功調度方法[J].自動化應用，2023，64（21）：183-185.

[6]姜煒超，沈冰，李昀，等.基于5G的含分布式電源智能分布式饋線自動化實現方法[J].供用電，2021，38（10）：57-63.

[7]王云會，鄭強仁，郭淼，等.含分布式電源與多元化負荷的配電網可靠性提升研究[J].電器與能效管理技術，2022（2）：63-67.