基于組合賦權-TOPSIS法的城市道路路段人行橫道合理間距研究

摘要 為確定城市道路設置路段人行橫道的合理間距，文章首先基于VISSIM仿真進行了路段人行橫道的間距模擬試驗，考慮安全與效率兩方面，獲取了各間距條件下的人車沖突次數、行人平均過街時間、機動車平均車速及通行能力4個評價指標；其次采用層次分析法及熵權法分別計算了各指標的主客觀權重，并通過組合賦權的方式確定了各評價指標的綜合權重；最后采用TOPSIS評價法對設置路段人行橫道的不同間距進行綜合評價。結果表明：主干路設置路段人行橫道的合理間距為300 m，次干路設置路段人行橫道的合理間距250 m。

關鍵詞 路段人行橫道；合理間距；組合賦權；綜合評價

中圖分類號 U491 文獻標識碼 A 文章編號 2096-8949（2024）21-0039-03

0 引言

城市道路路段人行橫道是城市步行交通系統中常見的平面行人過街設施，其科學合理設置可有效提升交通流的運行效率及安全性，然而我國現有研究對于路段人行橫道的設置間距多依據實踐經驗提供定性原則而非具體的量化標準，可能導致在實際工程應用中缺乏對交通運行環境的有效考慮。

目前國內外學者多通過設定不同的優化目標，如最小化行人繞行距離、最小化人車延誤等確定路段人行橫道的設置間距：Li W等[1]以過街行人的等待延誤時間為指標建立了路段人行橫道數量及位置的綜合優化模型；姚鵬[2]建立了基于定性和定量分析的“二階段”行人過街設施選址模型，并以行人步行距離之和最小為目標確定路段人行橫道設置方法；高彥超[3]綜合考慮行人可接受繞行距離、人行橫道設計通行能力及路段設計服務水平，確定了路段人行橫道合理間距取值的上下限。然而，多數學者研究僅以考慮人車運行效率作為指標依據，少有研究關注路段人行橫道設置對交通運行安全性的影響。因此，兼顧交通系統的安全性和運行效率確定城市道路設置路段人行橫道的合理間距具有重要意義。

1 基于VISSIM仿真的路段人行橫道間距模擬試驗

1.1 仿真參數設置

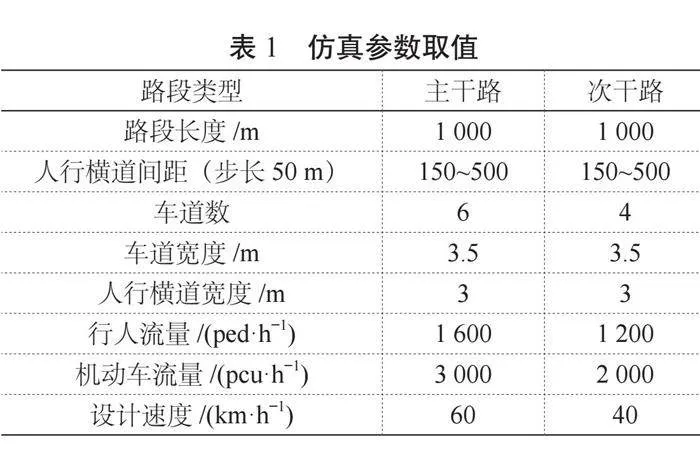
為獲取主次干路不同路段人行橫道間距條件下評價人車運行安全性及效率的相關指標，基于VISSIM軟件進行路段人行橫道間距模擬試驗，對各交通場景進行仿真。仿真運行前首先需進行場景搭建，輸入各類型路段所需的道路幾何參數和交通參數，依據我國《城市道路交通設施設計規范（2019版）》（GB 50688—2011）[4]，各道路類型仿真場景搭建的所需的參數取值如表1所示。

1.2 仿真結果輸出

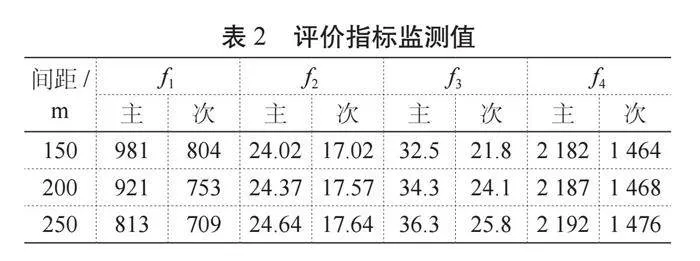
選取評價人車運行安全性的指標為人車沖突次數f1，次。選取評價人車運行效率的指標[5]分別為行人平均過街時間f2，s；機動車平均車速f3，（km·h?1）；機動車通行能力f4，（pcu·h?1）。仿真總時長設置為3 600 s，為排除仿真預熱階段的不穩定數據，以300 s作為仿真起點進行數據記錄，得到評價指標監測值如表2所示。

2 評價指標的組合賦權

2.1 主觀權重的確定

利用層次分析法（AHP）確定各評價指標主觀權重的步驟如下：

（1）依據專家意見對各維度指標的重要性進行評價，構建判斷矩陣A，并采用幾何平均法計算權重向量得到專家對各因素評判的權重。其中，權重向量Wi的計算如公式（1）所示：

Wi=（∏n j=1aij）1 n/∑n i=1（∏n j=1aij）1 n，（i，j=1，2，···，n） （1）

式中：aij——指標i相對于指標j的重要性標度；n——評價指標的個數。

（2）通過計算最大特征值λmax，確定一致性指標CI，并查表得到隨機一致性指標RI，計算二者比值得到一致性判斷統計量CR，可對判斷矩陣進行一致性檢驗。其中，最大特征值及一致性指標的計算如公式（2）～（3）所示。

λmax=（1/n）∑ n i=1（AWi）j/（nWi）j （2）

CI=λmax?n/n?1 （3）

式中：AWi——中矩陣AW的第i個元素。

該文共邀請5位專家對各指標進行評價打分，采用MATLAB計算各指標權重結果，如表3所示。

通過查表及計算得到隨機一致性指標為0.89，最大特征根為4.068 4，一致性指標為0.022 8，一致性判斷統計量為0.025 6小于0.1，結果通過檢驗。

2.2 客觀權重的確定

利用熵權法確定各評價指標客觀權重的步驟如下：

（1）分別依據對主干路及次干路的仿真樣本數據構建決策矩陣P并進行標準化處理，可得到標準化決策矩陣Xij。采用極值法，假設Xij為i個樣本第j個指標的數值，則指標Yij在其正向化及負向化兩種情況下的計算如公式（4）～（5）所示。

Yij=Xij?min（Xj）/max（Xj）?min（Xj） （4）

Yij=max（Xj）?Xij/max（Xj）?min（Xj） （5）

式中：i?[1，m]——評價對象的個數；j?[1，n]——評價指標的個數。

經計算，得到主干路及次干路的仿真樣本數據的標準化決策矩陣結果，如表4所示。

（2）計算每個樣本對評價指標的貢獻度，得到標準化決策矩陣。假設Pij表示i個樣本指標j占所有樣本總評分的比重，則其計算公式如下：

Pij=Yij/∑ n i=1Yij （6）

若Pij比重為0，則定義lim Pij→0 Pij×ln（Pij）=0。

（3）計算信息熵及指標權重，其中Qj表示第j個指標的信息熵，計算公式如下，則1?Qj為差異系數。

Qj=?[1/ln（n）]∑ n i=1（Pij×ln（Pij）） （7）

設Wj為第j個指標的權重，則其計算公式：

Wj=1?Qj/∑ n i=1（1?Qj） （8）

主干路及次干路評價指標的客觀權重計算結果如表5所示。

2.3 綜合權重的確定

結合上述兩種方法得到的各指標權重，采用組合賦權計算評價體系的綜合權重值Uj，即：

Uj=W1 j·W2 j/∑ 4 i=1W1 j·W2 j （9）

式中，W1 j及W2 j分別為層次分析法及熵權法計算的第j個指標權重結果。主干路及次干路評價體系的綜合權重結果如表6所示。

3 合理間距的TOPSIS決策模型

3.1 標準化加權決策矩的構建

經過上述分析已經得到了主干路與次干路樣本數據的標準化決策矩陣P及評價體系的綜合權重值Uj，將P與Uj相乘，得到各樣本數據的標準化加權決策矩陣，計算結果如表7所示。

3.2 各間距與正負理想解距離的確定

各評價對象的正負理想解是由每個評價指標的最佳或最差性能值組成的解，公式分別如下：

Y+={maxiyij|i=1，2，···，m;j=1，2，···，n} （10）

Y?={maxiyij|i=1，2，···，m;j=1，2，···，n} （11）

式中：Y+及Y?——各評價對象的正、負理想解。

采用歐氏距離法計算各人行橫道間距至理想正負解的距離，計算公式如下所示：

（12）

經上述計算，得到主干路各人行橫道間距與正負理想解距離D+ j、D? j及次干路各人行橫道間距與正負理想解距離D+ j '、D? j '如表8所示。

3.3 各相對貼近度的計算

對于每個路段人行橫道間距，其相對接近度是其到負理想解距離與到正負理想解總距離之和的比值，計算公式如（13）所示。相對接近度越高，表明其綜合性能越接近理想狀態；越低則反之[6]。

Tj=D? j /D? j +D+ j （13）

經計算得到主干路及次干路各人行橫道間距的相對貼近度及優劣排序分別如表9、表10所示。

由表可知，主干路路段人行橫道間距為300 m時的相對接近度最高，表明在主干路以300 m為間距設置路段人行橫道能夠在交通運行的安全性與效率方面提供最佳的綜合性能；次干路路段人行橫道間距為250 m時的相對接近度最高，表明在次干路上以250 m為間距設置路段人行橫道可提供最佳性能表現，因此該文推薦在城市主干路及次干路設置路段人行橫道的合理間距分別為300 m和250 m。

4 結論

該文通過VISSIM仿真對城市道路人行橫道的設置間距進行了模擬試驗，考慮安全與效率獲取了人車沖突次數、行人平均過街時間、機動車平均車速及通行能力4個評價指標，結合層次分析法和熵權法計算了評價指標的權重，并利用TOPSIS評價法進行了綜合評價。結果表明兼顧交通系統的運行效率和安全性，主干路和次干路人行橫道的合理設置間距分別為300 m和250 m。該研究不僅為城市道路人行橫道設置提供了科學的決策支持，也為后續相關研究提供了方法論參考，未來可進一步考慮不同交通流狀態下人行橫道設置間距的動態調整策略，以更精準地匹配實際交通需求，提升城市道路交通系統的整體性能。

參考文獻

[1]Li W， He J， Yu Q， et al. Using POI data to identify the demand for pedestrian crossing facilities at mid-block[J]. Sustainability， 2021（23）： 13256.

[2]姚鵬.行人過街設施設置的關鍵問題研究[D].成都：西南交通大學，2014.

[3]高彥超.路段平面過街設施合理設置研究[D].北京：北京工業大學，2015.

[4]中華人民共和國住房和城鄉建設部組織.城市道路交通設施設計規范：GB 50688—2011[J].北京：中國建筑工業出版社，2014.

[5]王天童，鄭長江，馬庚華，等.城市道路路段人行橫道通行能力分析[J].華東交通大學學報，2019（2）：4-5.

[6]馮芝梅，郭明洋，賀玉龍，等.基于組合賦權-改進TOPSIS法的城市慢行三網融合評價方法[J].交通信息與安全，2023（4）：163-172.