點支撐單向豎索幕墻有限元計算分析研究

【摘" " 要】：為了研究中建國際總部大廈單向豎索式幕墻結(jié)構(gòu)的受力性能，采用Midas FEA分別對3種索設(shè)計方案進行4種受力工況的有限元計算分析，綜合索的受力性能及成本，得出了最優(yōu)設(shè)計方案。

【關(guān)鍵詞】：幕墻；索結(jié)構(gòu)；點支撐

【中圖分類號】：TU382 【文獻標(biāo)志碼】：A 【文章編號】：1008-3197（2024）06-73-04

【DOI編碼】：10.3969/j.issn.1008-3197.2024.06.019

Point Support One -Way Vertical Cable Wall Finite Element Calculation Analysis Research

【Abstract】： In order to study the mechanical performance of the one-way vertical cable curtain wall structure of the China State Construction International Headquarters Building， this article uses Midas FEA to conduct finite element calculations and analyzes of four stress conditions for three cable design schemes， taking into account the impact of glass stiffness on the calculation results， and the mechanical performance and cost of the cable were comprehensively considered， and finally the optimal design solution was obtained.

【Key words】： curtain wall；cord structure；point support

隨著柔性支承結(jié)構(gòu)體系在點支式玻璃幕墻中的應(yīng)用越來越多，其結(jié)構(gòu)設(shè)計問題受到關(guān)注[1]。楊慶山等[2]研究了懸索結(jié)構(gòu)的分析方法，推導(dǎo)出3種有限元模式，并分別對計算結(jié)果進行了比較；舒暢[3]研究了單索支撐體系承載能力的影響因素；馮若強等[4]通過單層索網(wǎng)幕墻試驗，研究了玻璃面板對整個結(jié)構(gòu)受力體系的剛度貢獻作用。目前研究多集中于純索結(jié)構(gòu)的力學(xué)性能，實際工程中，受設(shè)計方案的影響，索的類型及布置形式多種多樣，索與其他結(jié)構(gòu)共同受力也十分常見。本文針對實際工程中遇到的設(shè)計問題，通過有限元分析，參考已有的設(shè)計及計算方法，得出不同方案的計算結(jié)果，為幕墻設(shè)計方案的選擇提供參考。

1 工程概況

中建國際總部大廈幕墻采用單向豎索式結(jié)構(gòu)作為點支式幕墻的支承結(jié)構(gòu)，整個幕墻體系由21根豎向索構(gòu)成，豎向索的跨徑為24.75 m。點支撐單向豎索幕墻由平面預(yù)應(yīng)力索面作為點支撐式幕墻的支承系統(tǒng)。幕墻由2塊矩形幕墻構(gòu)成L形立面，所處高度在75～100 m。見圖1。

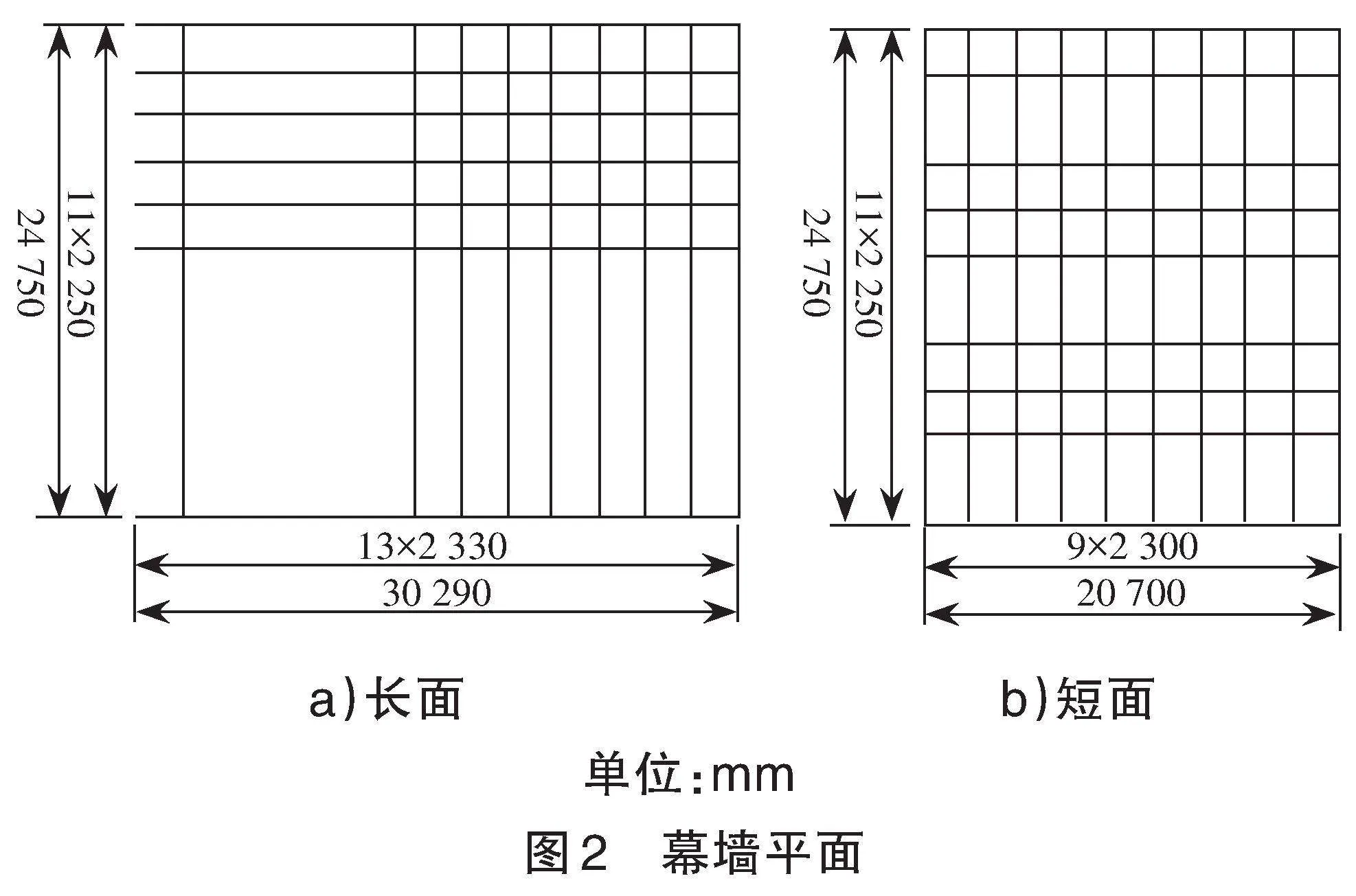
長面幕墻總寬為30.29 m，總高為24.75 m，由143塊寬2.32 m×高2.24 m的玻璃構(gòu)成，玻璃中間填充2 cm寬的硅酮膠進行密封。短面幕墻總寬為20.7 m，總高為24.75 m，由99塊寬2.29 m×高2.24 m的玻璃構(gòu)成，玻璃中間填充硅酮膠密封。見圖2。

整個幕墻體系由21根豎向索構(gòu)成。玻璃均采用8 mm+1.52 mmSGP+8 mm+12 mmA+8 mm+1.52 mmSGP+8 mm超白鋼化中空雙夾膠玻璃。

2 索方案設(shè)計

點支式玻璃幕墻指玻璃幕墻的分格以點連接形式將荷載及作用傳遞到中間支撐結(jié)構(gòu)的無金屬框、視野開闊的幕墻系統(tǒng)。它由玻璃幕墻的面板、玻璃連接器、中間支撐結(jié)構(gòu)構(gòu)成[1]。

點支式單向豎索幕墻的索受力時側(cè)向剛度會明顯減小，一個很小的側(cè)向荷載就可能引起桿件屈曲，這是由索的“幾何剛度”改變引起的，這種變形引起的幾何剛度變化不能被忽略。因此分析點支式單向豎索幕墻的時候必須慮索的P-Δ效應(yīng)及大變形效應(yīng)[5]，也就是幾何剛度變化引起的幾何非線性問題。為解決該問題，考慮3種布置方案。

1）方案一：在長面幕墻和短面幕墻連接處為減小幕墻拐角處變形量和拐角處拉索的變形設(shè)置平面索桁架。

2）方案二：在方案一基礎(chǔ)上在幕墻拐角處各增加2根魚腹式預(yù)應(yīng)力索[6]，初張力70 kN。

3）方案三：在方案一基礎(chǔ)上在長面幕墻和短面幕墻水平方向各增加3根?60 mm×8 mm鋼管。

3 有限元計算

3.1 模型建立

采用Midas FEA軟件對幕墻進行非線性有限元模擬分析。考慮玻璃在受到風(fēng)荷載和水平地震作用時內(nèi)外層存在荷載分配問題，為了更加真實模擬玻璃在荷載作用下的受力情況，玻璃和玻璃間的密封硅酮膠都采用三層復(fù)合板單元模擬。索采用拉勾式桁架單元模擬（FEA用拉勾式桁架單元模擬拉索）。為了真實模擬作用在玻璃上的荷載通過玻璃連接器傳遞到索的過程，玻璃連接器采用實體單元模擬，每個玻璃連接器的四只連接腳與玻璃剛性連接。索與玻璃連接器采用剛性連接連接[7]。見圖3。

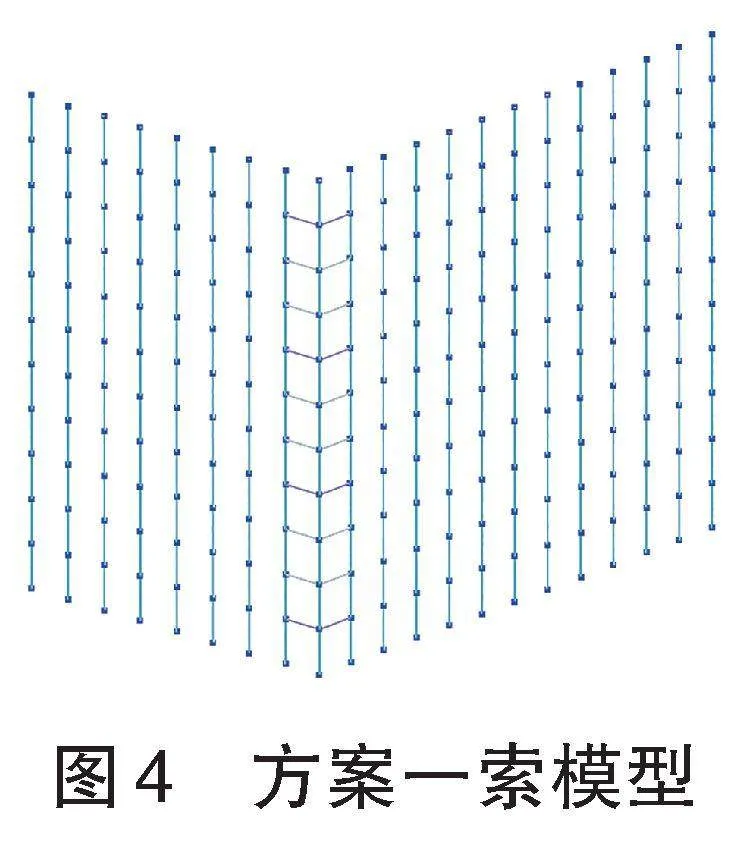
方案一：設(shè)置平面桁架索，用1D管單元模擬，與索鉸接。見圖4。

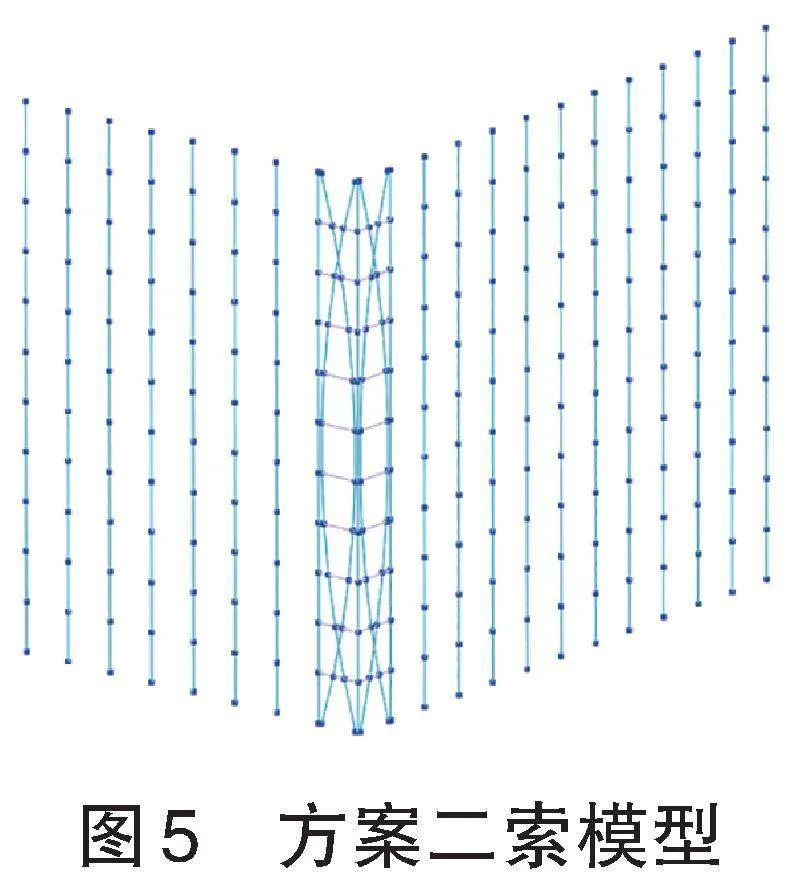
方案二：增加魚腹式預(yù)應(yīng)力索，拉索端部節(jié)點約束Dx、Dy、Dz。見圖5。

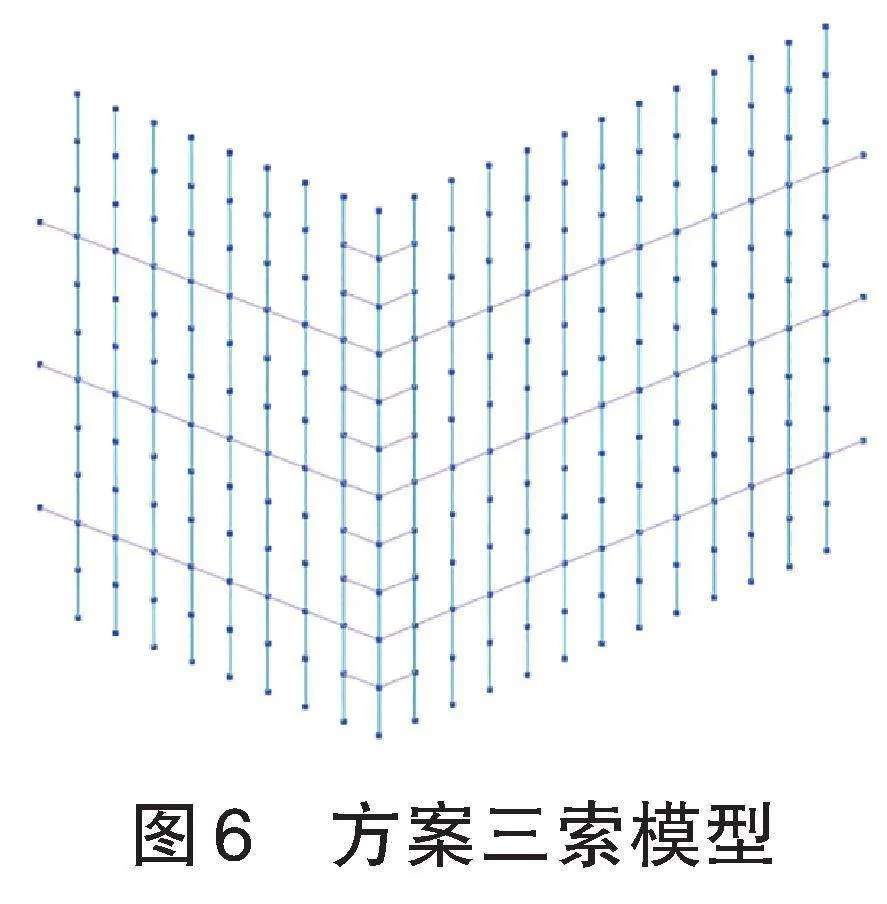
方案三：增加水平鋼管，鋼管與索鉸接，鋼管端部節(jié)點約束Dx、Dy、Dz、Rx、Ry、Rz。見圖6。

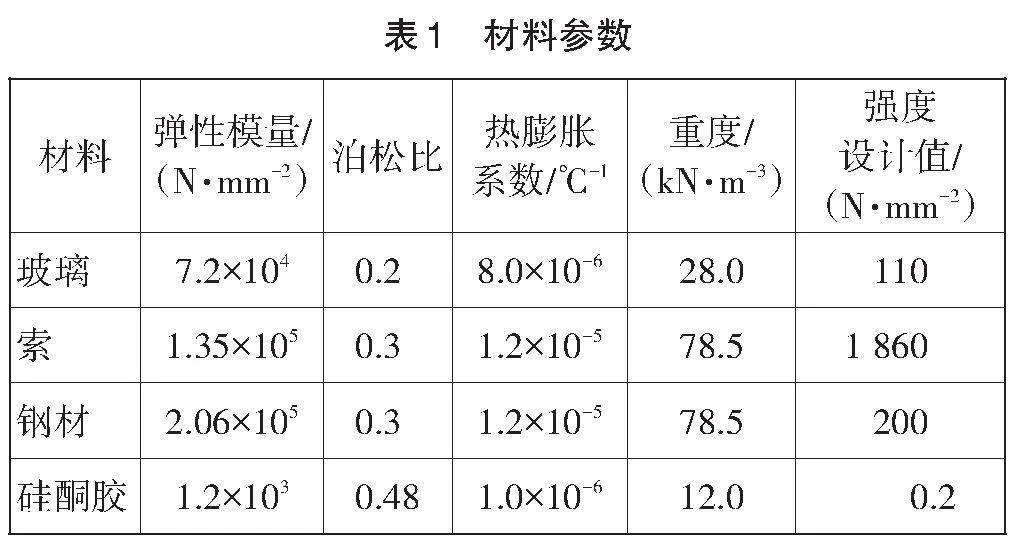
3.2 材料

幕墻結(jié)構(gòu)中所用的材料規(guī)格及強度均要滿足現(xiàn)行規(guī)范的要求。見表1。

3.3 計算荷載

荷載包括自重、風(fēng)荷載、索初張力、溫度作用、地震作用。

3.3.1 自重

通過重力加速度程序自動計算。

3.3.2 風(fēng)荷載

根據(jù)GB 50009—2012《建筑結(jié)構(gòu)荷載規(guī)范》取值，地面粗糙度為B 類，基本風(fēng)壓W0取0.45 kN/m2。驗算立面幕墻結(jié)構(gòu)時，墻面區(qū)體型系數(shù)為1.0，墻角區(qū)為1.32。在計算模型中墻角區(qū)為幕墻拐角處的兩列玻璃。

1）風(fēng)荷載標(biāo)準(zhǔn)值計算

墻面區(qū)wk=βgz μz μsW0=1.5×2.0×1.0×0.45=1.35（kN/m2）

墻角區(qū)wk=βgz μz μsW0=1.5×2.0×1.32×0.45=1.78（kN/m2）

式中：wk為風(fēng)荷載標(biāo)準(zhǔn)值，kN/m2；βgz為陣風(fēng)系數(shù)；μz為風(fēng)壓高度變化系數(shù)；μs為風(fēng)荷載體型系數(shù)。

2）風(fēng)荷載設(shè)計值

墻面區(qū)w=γwwk=1.5×1.35=2.025（kN/m2） （3）

墻角區(qū)w=γwwk=1.5×1.78=2.67（kN/m2） （4）

式中：w為風(fēng)荷載設(shè)計值，kN/m2；γw為承載能力極限狀態(tài)風(fēng)荷載作用效應(yīng)的分項系數(shù)，取1.5。

3.3.3 索初張力

為控制索在最不利荷載作用下的變形，取初張力為350 kN。

3.3.4 溫度作用

幕墻結(jié)構(gòu)考慮溫度影響，最大溫差取40 ℃，在進行承載能力極限狀態(tài)荷載組合時溫度作用的組合值系數(shù)取0.6，根據(jù)索的溫度變形關(guān)系

△T=F/（αEA） （5）

式中：△T為溫差，℃；F為索內(nèi)力，kN；α為線膨脹系數(shù)；E為彈性模量，N/mm2；A為截面面積，mm2。

單根?40 mm索在24 ℃溫差收縮時產(chǎn)生的索內(nèi)力約為100 kN。

3.3.5 地震作用

考慮水平地震作用對幕墻的影響，地震設(shè)防烈度7度，設(shè)計基本地震加速度值0.10g。

垂直于幕墻平面的水平地震作用標(biāo)準(zhǔn)值qEk=βEαmaxGK/A=[5×0.08×28×（1×1×0.032）]/（1×1）""" = 0.358 （kN/m2） （6）

式中：βE為地震動力放大系數(shù)，取5.0（為使脆性材料在設(shè)防烈度下部破損傷人而考慮）；αmax為水平地震影響系數(shù)，按抗震設(shè)防烈度和設(shè)計基本地震加速度查表；GK為幕墻構(gòu)件的永久荷載標(biāo)準(zhǔn)值；A為幕墻面積。

等效水平地震作用荷載標(biāo)準(zhǔn)值取0.36 kN/m2，將地震水平作用轉(zhuǎn)化為等效面荷載加載在幕墻2D單元面表面。

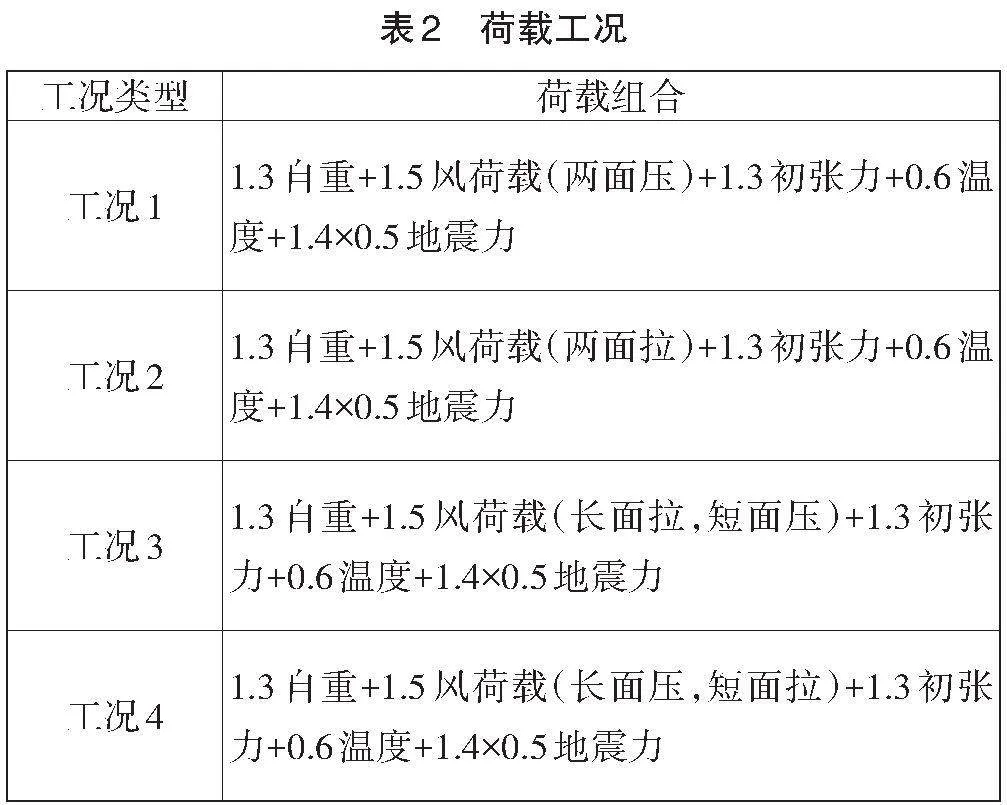
3.4 計算工況

針對幕墻兩面受壓、兩面受拉、長面受拉短面受壓，長面受壓短面受拉4種受力工況，計算最大索力、總索力、最大索撓度、玻璃最大應(yīng)力、單塊玻璃最大轉(zhuǎn)角及幕墻拐角處最大位移。見表2。

3.5 邊界和約束

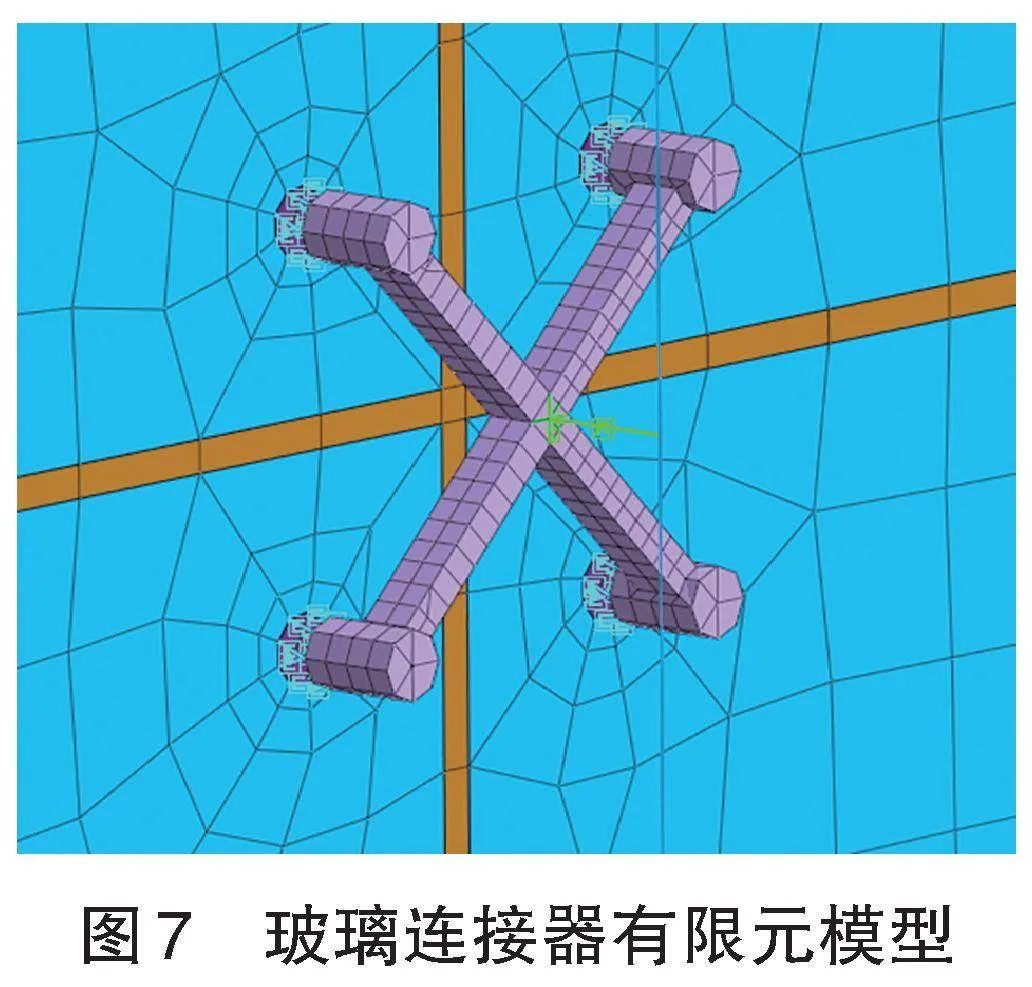
索與玻璃連接器采用剛性連接，每個玻璃連接器的連接腳與玻璃剛性連接。拉索端部節(jié)點約束Dx、Dy、Dz；長面幕墻邊緣節(jié)點約束Dy，短面幕墻邊緣節(jié)點約束Dx。見圖7。

3.6 計算結(jié)果

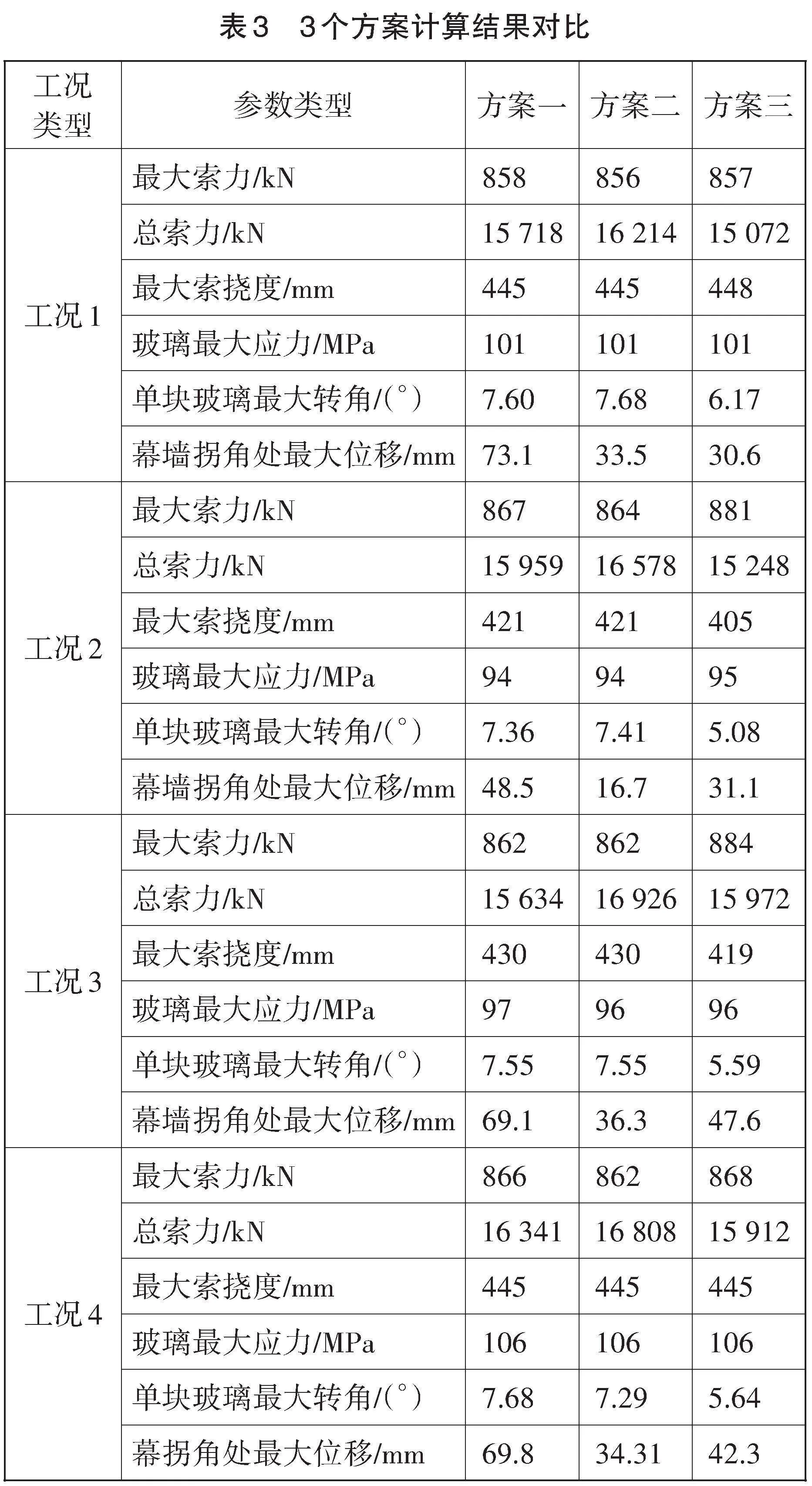
對比3個方案的計算結(jié)果，發(fā)現(xiàn)最大索力、索最大撓度、玻璃最大應(yīng)力，幕墻拐角處轉(zhuǎn)角幾乎一致，說明魚腹式索和水平橫桿對豎向直索的最大索力、豎向索最大撓度、幕墻拐角處轉(zhuǎn)角幾乎無影響。見表3。

綜合而言，方案二增加的魚腹式索和方案三增加的水平橫桿都可以明顯減小幕墻拐角處的位移。但方案一幕墻拐角處位移并不大（最大73.1 mm），使得增設(shè)的魚腹式索和水平橫桿意義有限。

此外，魚腹式索產(chǎn)生了至少500 kN的張力，會對索張拉端上部橫梁產(chǎn)生很不利的影響。同時，方案二幕墻拐角處增加的魚腹式索和方案三增加的水平橫桿均會影響幕墻的通透性和景觀視野且會增加整體造價。綜合考慮各方面因素，本項目選擇方案一。

4 結(jié)語

點支撐單向豎索幕墻利用桁架梁作為索邊緣固定結(jié)構(gòu)，采取對每根豎向高強鋼索施加預(yù)應(yīng)力，按設(shè)計受力狀態(tài)，形成單層平面預(yù)應(yīng)力索面作為點支撐式幕墻的支承系統(tǒng)。整個結(jié)構(gòu)通過在鋼索中施加預(yù)應(yīng)力使結(jié)構(gòu)體系保持人們可以接受的變形，另一方面又通過允許索結(jié)構(gòu)能產(chǎn)生較大的柔性變形而減少邊緣結(jié)構(gòu)構(gòu)件尺度，從而達到建筑設(shè)計通透、美觀的效果。荷載通過玻璃與索之間的連接器傳遞給了索，然后將荷載分配給索端桁架梁。點支式玻璃幕墻具有施工簡捷、通透性好的特性，迎合了人們回歸自然、享受陽光的需求。

本文通過對3種索設(shè)計方案進行有限元計算分析，得出了索、玻璃的應(yīng)力分布及變形值，并對比分析了各方案中幕墻拐角處位移值，結(jié)合構(gòu)件受力及外觀需求綜合比較，確定了最適合的索布置方案。

參考文獻：

[1]張炳順.拉索點支式玻璃幕墻力學(xué)性能研究[D].合肥：合肥工業(yè)大學(xué)，2015.

[2]楊慶山，沈世釗.懸索體系的有限元模式及其Newton型迭代法[J].哈爾濱建筑工程學(xué)院學(xué)報，1994，（6）：35-42.

[3]舒暢.點支式玻璃幕墻單索支承體系承載性能與工程應(yīng)用研究[D].北京：清華大學(xué)，2012.

[4]馮若強，武岳，沈世釗.單層平面索網(wǎng)結(jié)構(gòu)非線性頻率簡化計算方法研究[J].工程力學(xué)，2007，（10）：87-91+155.

[5]洪灶明，李曉彬，吳衛(wèi)國.空間懸索結(jié)構(gòu)的幾何非線性分析[J].交通科技，2008，（2）：13-14+18.

[6]楊立軍，孫晉，吳曉.點支式幕墻魚腹式索桁架支承體系動力特性[J].振動與沖擊，2010，29（6）：223-226+247.

[7]殷永煒，張其林，王丹，等.點支式玻璃幕墻索桁架支承體系的結(jié)構(gòu)性能研究[J].結(jié)構(gòu)工程師，2005，（2）：17-21.