基于優化動態窗口算法的智能機器人路徑規劃設計

摘 要：針對普通動態窗口算法進行動態避障后規劃路徑長度增加、在復雜環境中無法進行規劃的問題，本文研究一種優化智能機器人路徑規劃算法。本文采取設置動態函數、調整運動機制和規定運動航向等策略，保證算法可規劃最短路徑；利用軌跡評價函數構建最佳路徑的目標函數，提升機器人的避障性能，安全到達終點。使用蜂鳥云驗證，結果表明，與傳統哈里斯鷹算法相比，本文算法在復雜環境中規劃路徑更短，路徑質量更佳，運動時間更少，證明算法在路徑規劃中適用性較好。

關鍵詞：優化動態窗口算法；智能機器人；路徑規劃；傳統哈里斯鷹算法

中圖分類號：TP 242" " " " " " " " " " 文獻標志碼：A

路徑規劃的目的是使機器人利用行進準則搜索最佳的無碰撞路徑，根據環境掌握程度，機器人路徑規劃可分為全局規劃與局部規劃。全局規劃是了解環境后求解靜態環境中的最短路徑，局部規劃一般用于解決動態環境中的避障問題[1]。路徑規劃算法包括普通算法與優化算法，普通算法須提前載入信息，優化算法在既定環境中全局性較好。對路徑規劃優化算法研究較多，楊帆等[2]引入距離信息，在優化函數后得到最優路徑；黃勇強等[3]提出融合優化A*算法和動態窗口算法的路徑規劃算法，完成了全局修正；常新中等[4]將動態權重引入混合金豺優化算法，增強全局探索能力。

雖然上述研究提升了算法效率，但是存在依賴參數設定、在復雜地形中無法規劃等問題。優化動態窗口算法具有參數少、尋優速度快等優勢，因此選取該算法進行路徑規劃。在靜態全局規劃的基礎上進行實時動態規劃，使算法能夠有效應用于動態環境中，提升智能機器人規劃路徑的順滑度。

1 普通動態窗口算法

當應用于路徑規劃時，動態窗口算法起到有效避障的作用。在計算過程中，機器人速度約束條件如公式（1）所示。

（1）

式中：xt為機器人處于t時刻的線速度；yt為機器人處于t時刻的角速度；ymax為角速度最大值；xt+1為機器人處于t+1時刻的線速度；yt+1為機器人處于t+1時刻的角速度；mxmax為線加速度最大值；mymax為角加速度最大值；λt為時間步長。對速度空間進行采樣，獲得速度集合，在該過程中生成預測軌跡，使用評估函數評分后發現最佳運動軌跡與相應速度集合。評估函數g如公式（2）所示。

（2）

式中：x為機器人的線速度；y為機器人的角速度；k1、k2和k3為評估函數權重；r為歸一化過程；difference函數用于計算預測軌跡終端方位角與目標方位角的差值，差值越大，函數值越小；minimum函數用于計算預測軌跡所有坐標到障礙物的最佳距離，其評估預測軌跡與障礙物的距離，函數值越大，距離越遠；speed函數用于評估線速度與角速度，線速度越大，評分越高，角速度越慢。

如果需要算法全局搜索能力更強，則可增加k1數值；如果需要機器人避障能力更強，則可增加k2數值；如果需要機器人運動更順滑，則可增加k3數值。在實踐中，算法有2個需要調整的問題。1）避障后規劃路徑長度偶爾會增加。2）當靠近障礙物時，k2數值增加，搜索性能顯著降低。如果降低k2數值，就會觸碰障礙物，還會出現無法規劃路徑的問題。因此，本文提出優化動態窗口算法解決上述問題。

2 優化動態窗口算法

2.1 設置動態函數

在了解全局信息的情況下，優化動態窗口算法計算靜態最佳路徑，在沿該路徑運動的過程中，機器人不斷掃描環境，當發現動態障礙物時會主動避障，調整路徑。可能出現規劃路徑距離最佳路徑較遠的問題，為了使路徑更短，可在優化過程中添加dynamic動態函數，將其評估函數權重標記為k4。動態函數能夠使算法更快發現最短路徑，優化后的評估函數g如公式（3）、公式（4）所示。

（3）

式中：dynamic（x，y）為動態函數。

（4）

式中：l1、l2、l3、l4和l5為預估軌跡中5個均分點至坐標（a，b）

的最佳距離；ω為這5個點至最佳距離的平均加權數。當ω為最小值時，預估路徑最接近最佳距離，算法會優先選擇該路徑，因此算法規劃的路徑更接近最佳距離。

2.2 調整運動機制

當規避障礙物時，算法需要有較強的搜索能力和避障能力，當進行規劃時，普通動態窗口算法易出現權重系數不變的問題。如果動態障礙物速度較快，就會導致避障遲滯。因此，引入動態調整機制，當機器人靠近障礙物時，動態調整數值k2開始增加，避障能力顯著提升。計算機器人位置與障礙物的最佳距離，如公式（5）～公式（7）所示。

（5）

（6）

（7）

式中：wdo為機器人與障礙物之間的距離；（a1，b1）為機器人此時的坐標；（a2，b2）為障礙物此時的坐標；wdl為起點與終點之間的距離；（a3，b3）為起點坐標；（a4，b4）為終點坐標；xt為機器人處于t時刻的線速度；yt為機器人處于t時刻的角速度。k2數值與角速度成正比，與wdo成反比，距障礙物越近，k2數值越大，避障能力越好。

2.3 設定動態航向

在運動過程中，如果機器人與目標柵格存在角度差，則可能會繞行，因此本文提出以起點與首個目標點的連線水平夾角來設定動態航向。為避免錯誤選擇子目標點導致角度差，應在篩選周圍節點后根據距離設置評估函數。設（a3，b3）為起點坐標，（a5，b5）為無障礙物可行節點坐標，（a6，b6）為目標節點坐標。如果起點附近沒有障礙物，那么均為可通過區域，h為下一個可通過節點，根據可通過節點距離來計算函數u的具體數值，如公式（8）所示。

（8）

式中：n1為可通過節點距目標節點與當前節點之和的最佳路徑；n2為可通過節點距目標節點與當前節點之和的最長路徑。h越接近目標點，函數u越大；h越接近終點，函數u越小。算法優化后機器人會直接移動至下一個可通過節點，來避免路徑冗余。

3 算法路徑規劃過程

在既定環境中，優化動態窗口算法負責全局規劃，提取關鍵點作為局部目標點，當出現新增障礙物時進行局部規劃，保證全局路徑最佳。算法路徑規劃過程包括以下5個步驟。1）采用柵格法在蜂鳥云創建模擬地圖，對各個柵格進行編號，區分障礙物柵格與自由柵格，設置機器人的運動起止點。2）初始化處理算法參數，設時間步長λt、動態因子β、最大迭代次數Nmax、最大線速度xmax、最大角速度ymax、最大線加速度axmax和最大角加速度aymax等。3）令最大迭代次數Nmax=200，開始迭代，如果迭代次數達到最多，就可得到全局最佳路徑。4）提取局部子目標點，使用算法完成采樣，使用線速度與角速度（x，y）預測運動軌跡，根據結果選出最佳組合規劃局部路徑。5）判定局部子目標點，如果是全局目標點，則說明已到達終點，在輸出最佳路徑后結束運算。

4 仿真試驗與分析

為驗證算法有效性，采用不同算法進行仿真試驗。仿真平臺選用蜂鳥云，操作系統為Windows 11。采用柵格法對環境進行建模，將優化動態窗口算法與傳統哈里斯鷹算法進行比較，再將優化動態窗口算法放置在新增障礙物的模擬環境中進行試驗。

4.1 環境建模

采用柵格法構建節點能夠精確表現墻體、路面以及障礙物的位置，雖然存在部分傾斜與重影，但是不會對后續規劃產生影響。將機器人處理為小質點來忽略體積，降低誤差。柵格地圖環境大小為20 m×20 m，白色區域為自由區域，黑色柵格為障礙物，相鄰柵格距離為1 m。坐標（0，0）為原點，從左上至右下依次計數，坐標（1，19）為起點，坐標（19，1）為終點。

4.2 設置參數

傳統哈里斯鷹算法參數設置如下。粒子總數為50，動態因子β1=β2=2，最大迭代次數Nmax=200；優化動態窗口算法的參數設置如下。線加速度最大值axmax=0.2 m/s2，角加速度最大值aymax=20 rad/s，膨脹半徑Robstacle=0.2 m，評價函數權重系數分別為γ1=0.05，γ2=0.2，γ3=0.2，根據參數觀察軌跡。

4.3 靜態路徑規劃試驗

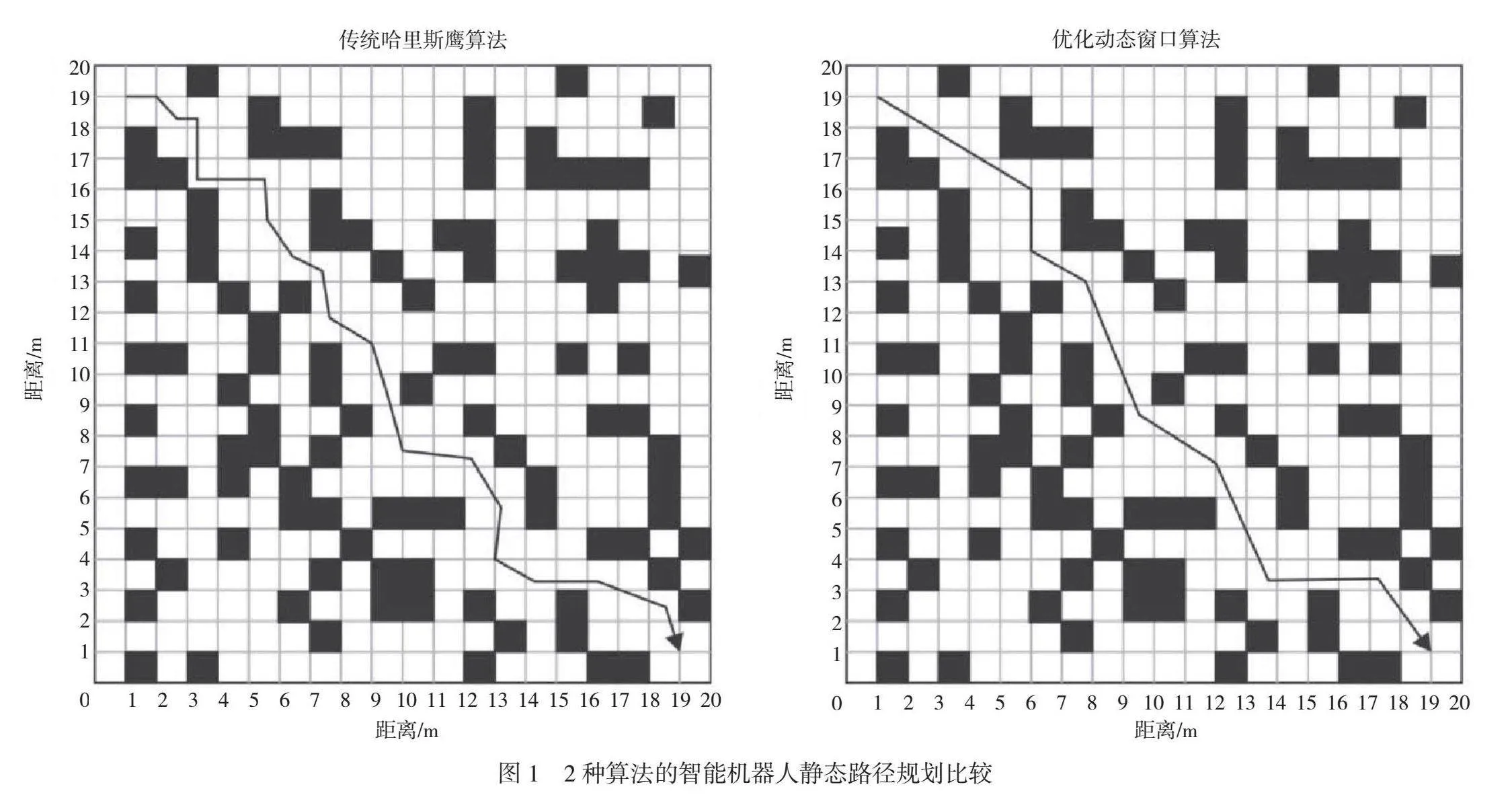
為檢驗在靜態布局地圖中路徑規劃算法的有效性，對2種算法在同一張地圖上進行試驗，智能機器人靜態路徑規劃比較如圖1所示，黑色實線為2種不同算法計算得到的運動軌跡，統計搜索節點數量、路徑長度、轉折次數、路徑節點數量以及時間，2種算法性能比較見表1。由表1可知，傳統哈里斯鷹算法規劃的路徑冗余點與轉折次數較多，當運動時會搜索許多節點，導致運行效率顯著降低；優化動態窗口算法規劃的路徑冗余點與轉折次數較少，與傳統哈里斯鷹算法相比，其運行效率具有一定優勢。

雖然2種算法目標點相同，但是優化動態窗口算法參與搜索的節點數量減少了18個，時間也縮短了1.33 s；對關鍵節點進行深度篩選后，路徑節點數量減少了11個，轉折次數減少了10次。優化動態窗口算法能夠減少轉折次數和搜索節點數量，節約計算時間。

4.4 動態路徑規劃試驗

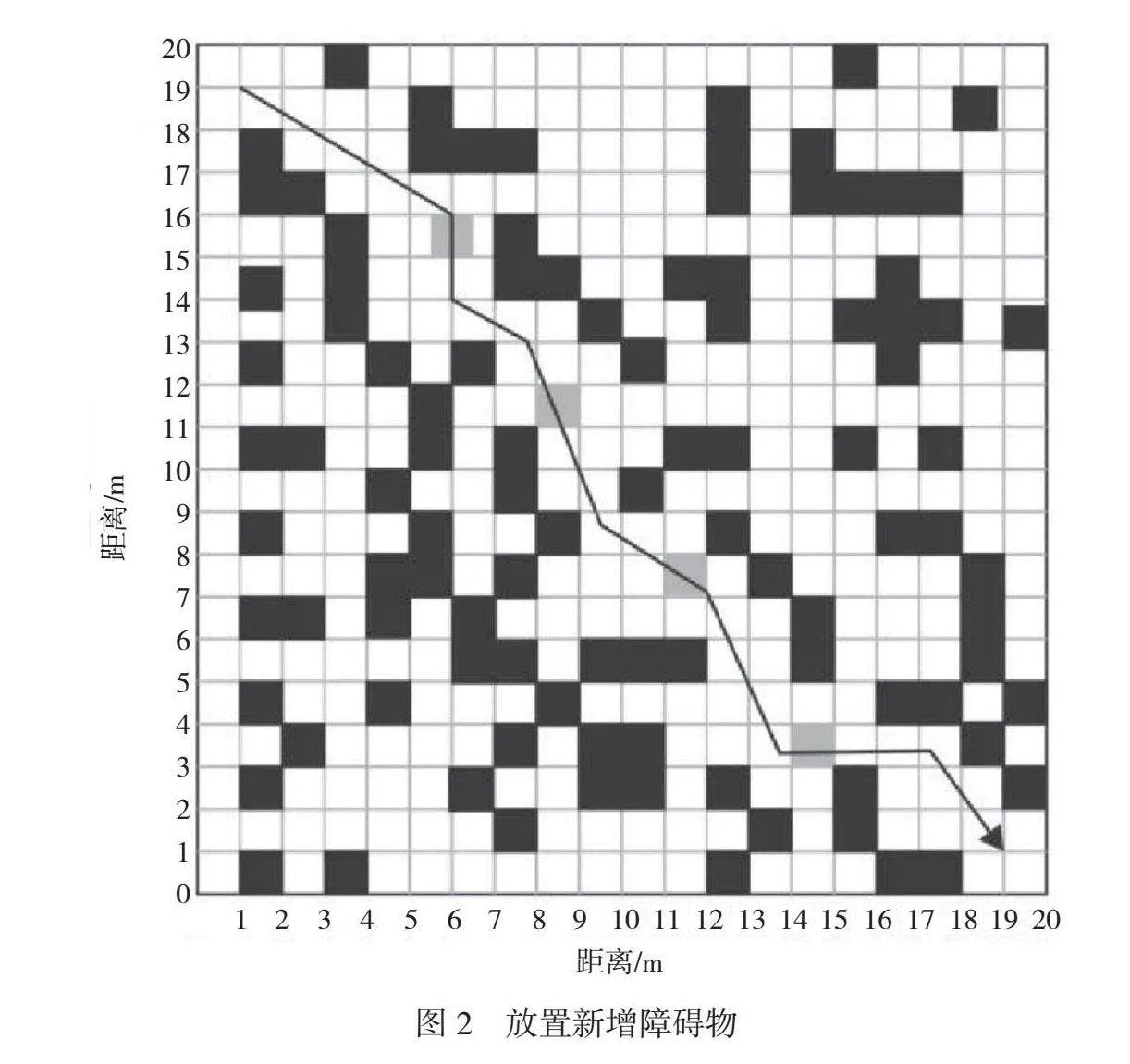
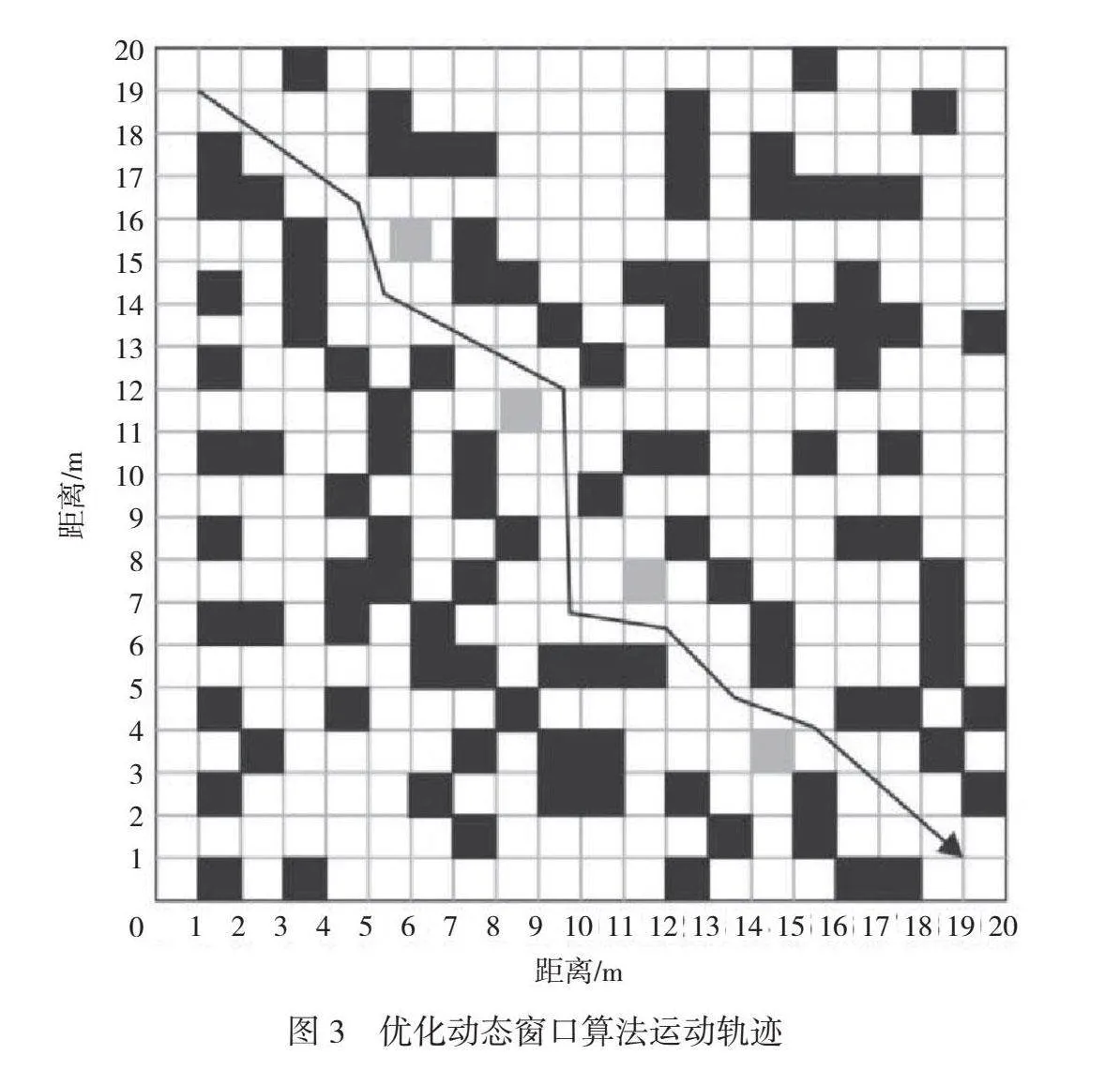
在柵格地圖的優化動態窗口算法的運動軌跡上放置灰色模塊作為新增障礙物（如圖2所示），并將2種算法進行對比試驗，由此驗證優化動態窗口算法的避障能力，優化動態窗口算法運動軌跡如圖3所示。

由圖3可知，如果新增障礙物處于全局最佳路徑，那么傳統哈里斯鷹算法不能有效避障，動態性能欠佳；優化動態窗口算法所得路徑在規避了所有新增障礙的基礎上更順滑，符合雙輪差速機械結構的運動特點，獲得了優質運動軌跡，證明了算法的有效性。

5 結語

綜上所述，當優化動態窗口算法應用于動態環境時，可顯著減少節點數量，提高運行效率，對關鍵節點進行深度篩選后能夠減少轉折次數，解決了當運動時無法躲避新增障礙物的問題，提升了軌跡順滑度，保證在最佳全局路徑上，機器人可實時避障。本研究僅在新增障礙物的環境下進行仿真試驗，未過多關注移動障礙物，在后續研究中可將其作為參照，提升應用效果。

參考文獻

[1]黃敬堯，劉洪宇，武慧慧，等.基于改進的五行環算法的移動機器人路徑規劃[J].傳感器與微系統，2023，42（10）：143-146.

[2]楊帆，李瑋，嚴天宏.基于梯度優化的移動機器人路徑規劃算法[J].現代電子技術，2023，46（21）：99-104.

[3]黃勇強，劉硯菊，宋建輝，等.基于改進A*算法與優化DWA的差速移動機器人路徑規劃[J]. 沈陽理工大學學報，2023，42（6）：25-33.

[4]常新中，岳哲鵬，郜海超，等.基于改進粒子群的混合金豺優化算法的移動機器人路徑規劃[J].中原工學院學報，2023，34（4）：24-29.