基于改進螢火蟲算法的充電樁選址定容優化方法

摘 要：針對當前充電樁選址定容不合理，導致電動汽車充電效率低的問題，本文引入改進螢火蟲算法，研究充電樁選址定容優化方法。分析電動汽車出行時空特性，計算電動汽車充電負荷。以充電樁在一個運行周期內的費用最小化為目標，建立充電樁選址定容模型。利用改進螢火蟲算法求解模型，得到最佳選址定容結果。對比試驗證明，應用新的方法選址定容可以合理規劃充電樁，提升電動汽車充電效率。

關鍵詞：改進螢火蟲算法；定容；充電樁

中圖分類號：U 491" " " 文獻標志碼：A

充電樁的選址需要符合城市規劃、土地使用權等相關要求[1]。所選區域要具備可靠的電力供應，以保證充電樁正常運行。在選址過程中，須考慮噪聲、污染物等因素，以減少對環境的影響[2]。許多學者對充電樁選址定容問題進行研究。當前研究側重于充電樁的選址策略，考慮電動汽車的行駛軌跡和充電需求，以確定最佳的充電樁位置，提出基于多目標優化的充電樁選址方法。部分研究人員考慮交通流量和土地成本等因素，提出一種基于模擬退火算法的充電樁選址策略。還有一些研究探討了充電樁定容的問題，提出了基于區間估計的充電樁容量規劃方法，以確定滿足電動汽車充電需求的充電樁容量[3]。根據相關文獻可知，充電樁選址定容問題的研究已經取得了一定進展，這些成果為深入研究提供了參考。在以上研究的基礎上，本文將研究基于改進螢火蟲算法的充電樁選址定容優化方法。

1 電動汽車出行時空特性分析與電動汽車充電負荷計算

在電動汽車充電設施建設中，充電樁的選址和容量規劃是非常重要的環節。電動汽車出行的時空特性會直接影響充電樁的選址和定容的決策，有以下3個方面的影響。1）行駛距離。在充電樁選址過程中需要考慮用戶出行的行駛距離。如果電動汽車的行程較短，那么需要在交通樞紐、商業區等處設置充電樁，以便用戶能夠更方便地補充充電。如果電動汽車的行駛距離較長，充電樁可以更多地布置在長途出行的道路上，使用戶在行駛過程中快速充電。2）行程結束時間。在充電樁選址過程中需要考慮用戶行程結束時間分布情況。分析電動汽車行駛終點時刻的威布爾函數擬合結果，可以了解用戶的行程結束時間分布情況。根據該情況合理安排充電樁的位置和數量，以滿足用戶在各時間段的補充充電需求。3）用戶出行密度。電動汽車的時空特性會影響充電樁的容量規劃。如果某個區域的電動汽車出行密度較高，那么在該區域設置的充電樁容量應相對較大，以滿足更多用戶的充電需求。在電動汽車出行密度較低的區域，可以適量減少充電樁設備的容量。充電樁的選址定容會受電動汽車出行時空特性影響，因此須分析電動汽車的行程結束時間分布和行駛距離分布。威布爾函數可以很好地擬合隨機數據，在各種類型的數據擬合中應用廣泛。采用三參數威布爾函數擬合電動汽車行駛終點時刻，如公式（1）所示 [4]。

（1）

式中：f（x，k，c，γ）為電動汽車行程結束時間擬合結果；x為隨機變量；k為形狀參數；c為尺度參數；γ為位置參數，參數選取直接影響函數擬合效果，威布爾函數的分布曲線由參數k、c確定，其形狀參數為無量綱值，與威布爾函數曲線的峰值有統計學意義；c的單位為min，根據車輛行駛至終點的時間確定該參數。

結合用戶行程數據分析行駛距離分布，居民行駛里程近似服從正態分布，因此其分布概率密度函數如公式（2）所示。

（2）

式中：fD（d）為行駛距離分布的概率密度函數；μD為電動汽車每次行程的期望里程數；σD為正態分布標準差；d為居民行駛實際里程。在該基礎上，深入分析電動汽車行程時空分布，建立出發點為用戶所在地的典型出行鏈（如圖1所示）。

圖1有4個典型的出行鏈，分別為用戶在家-工作場所-社交/購物/其他場所、用戶在家-購物場所-社交/工作/其他場所、用戶在家-其他場所-社交/購物/工作場所和用戶在家-社交場所-工作/購物/其他場所。以上述4個出發點為用戶所在地的典型出行鏈，結合用戶1 d的出行數據，分析該群體的出行行為規則，得出了該群體的平均出行軌跡系數為3.02。在分析過程中，如果某一次出行鏈的系數大于3，那么說明選址定容優化方法的充電樁最佳選址和容量結果與實際情況相吻合。例如，用戶先去學校再回到家中，在這個過渡階段，電動車通常不會充電，因此假設用戶在中途的一小段時間內沒有充電[5]。為便于分析，將從家出發到一地的情形定義為4條出行鏈。

綜上所述，對相同目的的電動汽車充電公里數疊加求和，得到在規定區域范圍內任意目的地的充電功率，如公式（3）所示。

（3）

式中：Pn，t為某個目的地n在24 h內的充電負荷；Pcn為電動汽車的充電功率；Nhn為充電的電動汽車總數量；Pnk，t為用戶在n對電動汽車進行充電的概率；k為第k個充電的電動汽車。根據公式（3）計算電動汽車充電負荷，為后續充電樁的選址定容提供依據。

2 建立充電樁選址定容模型

綜合考慮建設費用、運維費用和電網購電費用，建立一個數學模型，并確定一個最優選址規劃目標，最小化充電樁系統的總體成本。在選址過程中權衡各種因素，選擇最適合的地點、容量和配置方式，為用戶提供高效、經濟和可持續的充電服務。因此，當對充電樁進行選址規劃時，須考慮各種因素，確定最佳選址規劃目標，如公式（4）所示。

（4）

式中：minC為以充電樁在一個運行周期內的費用最小化為目標的最佳選址規劃函數；C1i、C2i、C3i、C4i和C5i分別為第i個充電樁的每年投資費用、維護檢修費用、電能損耗費用、輔道建設費用和平均電能消耗成本。在對電動汽車每日充電需求進行分析的過程中，根據經過交叉口的車輛數來確定交叉口處的交通流，計算充電站中配備的充電機數量。由于交叉口中的車輛可以從2個不同的方向行駛，因此在統計1個節點中的車輛數量的過程中，應該以出站和進站的方向統一為準則，防止重復計算。在T時段中，在1個充電站中應配置的充電樁數量mi如公式（5）所示。

（5）

式中：qjcar、qjbus為每天從路口j前往充電站進行充電的電動汽車數量和公交車數量；Scar、Sbus為電動汽車和公交車的平均充電容量；ρ為充電電量裕度；P為額定功率；kx為平均充電效率；Tv為充電時長；kt為出行時間價值。將公式（4）和公式（5）作為充電樁選址定容模型，為保證模型成立，設置約束條件為充電站數量應大于或等于充電站應建設數量最小值，小于或等于充電站應建設數量最大值，充電樁數量應控制在充電樁目標上限和下限范圍內。

3 基于改進螢火蟲算法的模型求解

結合改進螢火蟲算法對構建的充電樁選址定容模型進行求解，得到最佳的充電樁選址定容結果。改進螢火蟲算法的原理是利用模擬螢火蟲的閃爍行為來進行優化。螢火蟲的閃爍行為可以作為信號吸引其他螢火蟲個體。在算法中，每1個螢火蟲代表1個解，亮度代表解的質量，亮度越高，該解質量越好，這個候選方案在優化目標方面越優秀。在螢火蟲算法中，亮度高的螢火蟲會吸引亮度低的螢火蟲，引導整個群體向更優解方向移動。利用以上原理，在充電樁選址定容優化問題中，根據螢火蟲算法求解最佳充電樁位置和容量，最大程度地提高充電效率，提高用戶體驗，降低建設成本。不斷地迭代和更新螢火蟲的位置和亮度，最終找到最優解。綜上所述，確定改進螢火蟲算法中狀態變量的余數違反總值Svio（ui），如公式（6）所示。

（6）

式中：gj（x，ui）為與第j個狀態變量相關的不等式約束條件；c為與狀態變量相關的不等式數量；G為控制變量和狀態變量不等式的總數；j為第j個狀態變量。根據上述條件，為更好地對模型進行優化求解，引入非劣分層排序，改變螢火蟲移動步長因子，搜索最優解。單個螢火蟲群落的總費用是若干個充電站的費用總和。在實際應用中，為了更好地解決問題，螢火蟲群間的相互吸引力會隨著距離增加而減少，避免任意聚集于一點的現象，得到最佳選址定容結果。

4 對比試驗

試驗旨在驗證基于改進螢火蟲算法的選址定容優化方法在實際應用中的可行性與可靠性。在試驗開始前，收集某城市的電動汽車數量、行駛軌跡和充電需求等相關數據，并對數據進行預處理和清洗，保證數據準確、完整。將改進螢火蟲算法應用于實際數據，并與傳統算法（例如貪婪算法、遺傳算法）進行對比試驗。在相同的試驗條件下評估不同的算法。根據試驗數據的特點和實際需求，調整了改進螢火蟲算法的參數，包括螢火蟲群體的規模、亮度更新因子等。將螢火蟲群體規模設定為20～50，將亮度更新因子設定為0.5～1.0。根據其他算法特點對相應的參數進行設置。充電樁選址定容與電動汽車的充電效率有統計學意義。為保證試驗結果客觀，選擇6種不同品牌的電動汽車作為試驗對象，分別為特斯拉Model Y、比亞迪漢EV、理想ONE、蔚來EVE、小鵬P7以及長安歐拉。將充電效率作為評價3種方法應用效果的指標，評估充電樁為電動汽車提供充電服務的平均速度。充電平均速度計算過程如公式（7）所示。

v=W/t " " " " " " " " " " " （7）

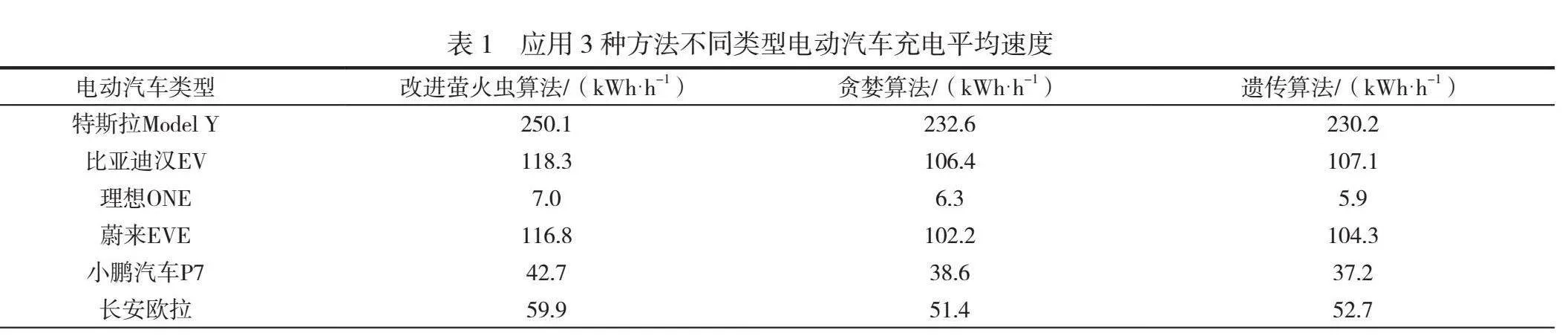
式中：v為充電平均速度；W為充電量占比；t為充電時間。充電平均速度見表1。

從表1中記錄的數據可以看出，應用改進螢火蟲算法，各類型電動汽車的充電平均速度均高于對比方法，特斯拉Model Y的充電平均速度為250.1 kWh/h，應用貪婪算法和遺傳算法后該汽車的充電平均速度分別為232.6 kWh/h和230.2 kWh/h，充電時間過長，影響充電服務質量和效率。因此，由試驗結果可知，基于改進螢火蟲算法的選址定容優化方法更有優勢。為了進一步驗證設計方法的有效性和可行性，以選址定容優化方法得出結果與實際結果的吻合度為評估指標，分析選址定容優化方法的性能，如果吻合度較高，則說明采用選址定容優化方法，充電樁選址和容量與實際吻合，即誤差較小。為了試驗的可靠性，在該試驗中，采用貪婪算法的選址定容方法（簡稱貪婪算法）和遺傳算法的選址定容方法（簡稱遺傳算法）作為對比方法，與本文設計的基于改進螢火蟲算法的充電樁選址定容優化方法（簡稱改進螢火蟲算法）進行對比，不同充電樁選址定容方法的吻合度結果見表2。

根據表2可知，在多個樣本進行試驗后，不同方法得出的充電樁選址定容結果與實際結果的吻合度較高，說明3種方法得出的結果接近實際結果。經過詳細分析，改進螢火蟲算法的吻合度較高，評估指標均高于99.00%，最高值為99.75%，最低值為99.37%；貪婪算法的評估指標最高值為98.64%，最低值為98.16%；遺傳算法的評估指標最高值為98.99%，最低值為97.29%，改進螢火蟲算法的吻合度比對比方法提高了0.7%以上。說明本文設計的基于改進螢火蟲算法的充電樁選址定容優化方法得到的結果與實際結果更契合，本文方法更符合實際需求。當設計本文方法時，充分考慮了電動汽車出行的時空特性會直接影響充電樁的選址和定容的決策。

5 結語

本文介紹了一種充電樁選址定容優化方法，旨在滿足電動汽車用戶的充電需求，降低充電樁的建設成本，提高其運行效率。充電樁選址定容優化是一個意義重大、應用廣泛的課題。在目前的研究中，充電樁選址定容問題主要考慮了土地資源、交通流量、電力供應和環境因素等方面。隨著電動汽車普及和充電需求增長，未來研究可以進一步考慮其他影響因素，例如城市規劃、政策支持和用戶行為等。隨著問題復雜性增加和研究需求擴大，未來研究可以探索更復雜和高效的數學模型和優化算法，例如動態規劃、強化學習等。綜上所述，未來可以從多個方面深入研究充電樁選址定容優化，以滿足電動汽車用戶的需求，促進電動汽車產業的發展，提高城市能源利用效率和環境保護水平。

參考文獻

[1]郄佩琦，陳傳軍，陳佳梁，等.基于區域繁忙度的AGV充電樁選址研究[J].制造業自動化，2023，45（8）：214-220.

[2]甄西媛，高超，李向華，等.基于電動出租車數據的充電樁選址聚類方法比較[J].汽車工程學報，2023，13（4）：564-573.

[3]楊佳楠，孫秉珍，潘娣，等.基于BWM的改進區間VIKOR模型及其在新能源汽車公共充電樁選址決策中的應用[J]. 數學的實踐與認識，2023，53（4）：10-23.

[4]劉曉天，傅軍，趙思翔，等.基于二層規劃并計及負荷預測的電動汽車充電樁選址定容方法[J].電測與儀表，2021，58（5）：144-150.

[5]俞曉吉，袁晟，黃善南，等.基于拓撲理論與異常算法的交流充電樁布局選址方法[J].電子設計工程，2023，31（12）：155-159.