抗速度欺騙干擾的雷達發射波形與接收濾波器聯合設計方法



摘 要: 作為一種經典的有源干擾,速度欺騙干擾極易導致雷達在多普勒維上同時檢測到單個或多個虛假目標,造成雷達虛警,給雷達探測帶來了巨大挑戰。為了抵抗速度欺騙干擾,結合脈內、脈間編碼和接收濾波器設計等多個自由度,提出一種發射與接收多維聯合設計的方法。首先,以非匹配濾波器峰值損失為懲罰項,并聯合接收信號的多普勒譜上目標旁瓣能量與干擾能量構建優化目標函數,同時考慮發射波形峰均功率比約束。然后,基于坐標下降思想和優化最小化理論,提出一種塊坐標下降的優化最小化方法求解該問題。最后,仿真實驗表明相比傳統脈間初相設計,在頻譜阻帶內,所提方法峰值旁瓣比提升約6 dB,抗速度欺騙干擾性能大幅提升。
關鍵詞: 波形設計; 干擾抑制; 速度欺騙干擾; 非匹配濾波器
中圖分類號: TN 974
文獻標志碼: A
DOI:10.12305/j.issn.1001-506X.2024.08.06
Joint radar transmitted waveform and received filter design approach
against velocity deception jamming
ZHANG Mingxing1, SHI Qiao1, YU Tao2, ZHOU Zhengchun1,*, CUI Guolong3
(1. School of Information Science and Technology, Southwest Jiaotong University, Chengdu 610031, China; 2. School
of Mathematics, Southwest Jiaotong University, Chengdu 610031, China; 3. School of Information and Communication
Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China)
Abstract: As a typical active jamming, velocity deception jamming can cause radar to detect single or multiple 1 targets in Doppler dimension at the same time, resulting in 1 alarm and posing a huge challenge to radar detection. A joint radar transmitted waveform and mismatched filter design method focus on suppressing the velocity deception jamming is proposed, which comprehensively considers many degrees of freedom such as intra-pulse, inter-pulse coding and receiver filter. Firstly, the peak loss of unmatched filter is taken as the penalty term, and the optimization objective function is constructed by combining the target sidelobe energy and interference energy on the Doppler spectrum of the received signal, and the peak-to-average power ratio constraint of the transmitted waveform is considered. Secondly, the block coordinate descent majorization-minimization method is proposed to solve this problem, based on the coordinate descent method and majorization-minimization theory. Finally, the simulation results show that compared with the traditional pulse to pulse initial phase design, the against velocity deception jamming performance of the proposed method is greatly improved, specifically, the peak sidelobe ratio is increased by about 6 dB in the special stopband.
Keywords: waveform design; jamming suppression; velocity deception jamming; mismatched filter
0 引 言
隨著數字射頻存儲(digital radio frequency memory, DRFM)技術的發展,現代干擾機能夠實現對雷達信號的存儲、復制和轉發,并在轉發信號時調制虛假的時延、頻率和幅度等進行欺騙干擾。這些干擾信號與真實信號在時域、頻域和空域的特征非常相似,給雷達系統帶來了嚴峻挑戰[1-2]。
根據DRFM干擾機調制和轉發信號方式的不同,欺騙干擾主要有距離欺騙干擾、速度欺騙干擾和靈巧干擾等。波形設計作為雷達系統抗欺騙干擾的關鍵技術之一[3-4],近年來引起了國內外學者的廣泛關注。目前,基于波形設計抗欺騙干擾技術的研究主要集中于發射波形設計和發射波形與接收濾波器聯合設計兩方面。
由于干擾機需要一定時間對雷達信號進行捕獲、分析和識別,因此通常干擾信號將滯后于雷達信號。文獻[5]首次提出了在不同的脈沖重復間隔(pulse repetition interval, PRI)中發射調頻斜率隨機擾動的線性調頻波形,實現了較好的抗距離欺騙干擾性能。在此基礎上,文獻[6-7]在不同PRI中發送正交碼,并在接收端采用匹配濾波器,實現了在特定距離單元內有效地進行抗距離干擾目的。文獻[8-11],建立了最小化發射信號的積分旁瓣電平(integrated sidelobe level, ISL)和干擾信號的干擾積分電平(jamming integrated level, JSL)加權和的優化準則,在峰值約束條件下,采用了發射波形與接收濾波器交替優化的方式,實現了抗間歇式采樣干擾。同樣采用交替優化的方法,文獻[11]采用多脈沖互補序列和接收濾波器聯合設計的方式,提升了在間歇式采樣干擾下對運動目標檢測的能力。文獻[12-13]通過分析雷達回波信號的時頻域特征,在時頻域上實現了間歇式采樣干擾的參數識別和抑制。
上述工作主要是針對抗距離欺騙干擾和抗靈巧干擾,針對速度欺騙干擾同樣有大量的研究[14-21]。文獻[14]利用二元相位編碼偽隨機波形,實現了低干信比(jamming-to-signal ratio, JSR)干擾背景下的速度欺騙干擾抑制,由于干擾信號的能量將會均勻分布在整個多普勒頻譜上,因此當JSR較大時,該方法將失效。為此,Zhang等[15]利用多通道處理技術對干擾參數進行了估計,并基于相位梯度算法提出了一種自適應脈間波形初始相位編碼的方法。該方法通過最小化阻帶范圍內干擾信號多普勒頻譜能量的方式,實現了在強電子干擾環境下對速度欺騙干擾的抑制。在此基礎上,文獻[16]和文獻[17]分別基于修正牛頓法和序貫估計算法進一步提升了抗干擾性能。隨后,文獻[18-19]基于快速傅里葉變換(fast Fourier transform, FFT)提出了加權循環(weighted cyclic algorithm-new, WeCAN)算法,考慮了多目標多干擾場景下抗速度欺騙干擾。此外,文獻[20]通過設計自適應迭代濾波算法考慮抑制距離-速度聯合欺騙干擾抑制問題。葛萌萌等[21]考慮了脈間波形幅度設計這一自由度,建立了最小化阻帶內干擾信號能量和目標信號旁瓣的優化問題,提出非精確交替方向懲罰法(inexact alternating direction penalty method, IADPM),該算法實現了脈間波形幅度相位聯合設計抗速度欺騙干擾。上述基于波形設計的抗速度欺騙干擾方法均取得了較好的抗干擾效果。但是,其均只通過設計脈間初相或者幅度來實現干擾抑制,并且在雷達接收端仍采用傳統的匹配濾波處理,波形設計自由度有限。
為了充分利用脈內脈間波形與接收濾波器的自由度,本文提出一種脈內波形和接收端濾波器聯合設計抗速度欺騙干擾的方案。首先,在發射波形峰均能量比(peak-to-average power ratio, PAPR)約束和接收濾波器能量約束下,建立最小化阻帶范圍內干擾信號能量和目標能量的加權優化問題。此外,為了避免非匹配濾波造成峰值增益損失,基于罰函數方法,在目標函數中引入了峰值約束函數。然后,采用發射波形和濾波器交替迭代的方式實現了優化問題求解,采用一種加速迭代算法,大幅提升了算法收斂速度。最后,仿真實驗表明,相對于傳統設計脈間波形抗速度欺騙干擾方法,采用本文設計脈內波形與接收濾波器具有更好的抗速度欺騙干擾性能,能夠實現多目標多干擾場景下的速度欺騙干擾抑制。
1 信號模型
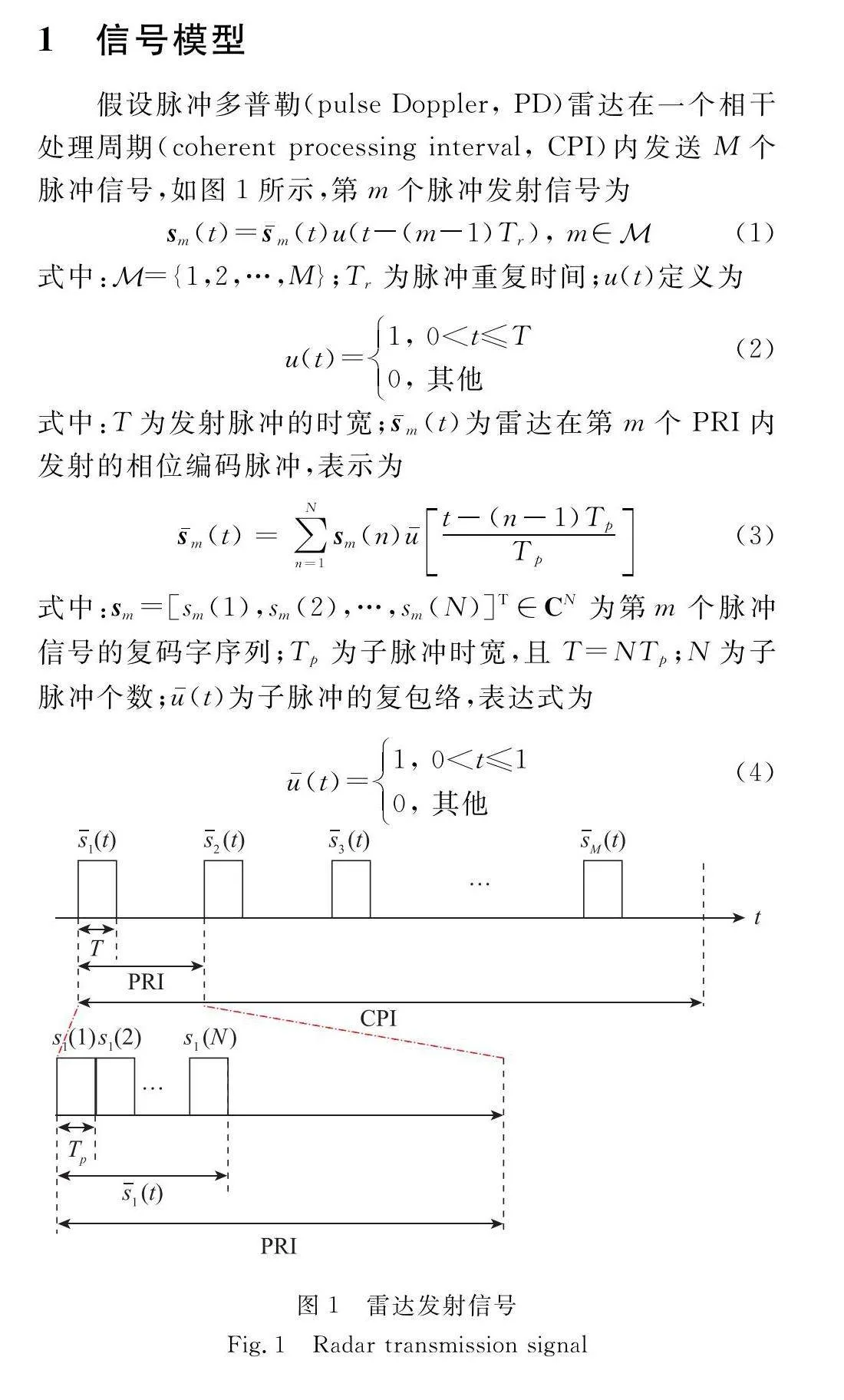
假設脈沖多普勒(pulse Doppler, PD)雷達在一個相干處理周期(coherent processing interval, CPI)內發送M個脈沖信號,如圖1所示,第m個脈沖發射信號為
sm(t)=s-m(t)u(t-(m-1)Tr), m∈M(1)
式中:M={1,2,…,M};Tr為脈沖重復時間;u(t)定義為
u(t)=1, 0lt;t≤T
0, 其他(2)
式中:T為發射脈沖的時寬;s-m(t)為雷達在第m個PRI內發射的相位編碼脈沖,表示為
s-m(t)=∑Nn=1sm(n)u-
t-(n-1)TpTp
(3)
式中:sm=[sm(1),sm(2),…,sm(N)]T∈CN為第m個脈沖信號的復碼字序列;Tp為子脈沖時寬,且T=NTp;N為子脈沖個數;u-(t)為子脈沖的復包絡,表達式為
u-(t)=1, 0<t≤1
0, 其他(4)
對于高重頻PD雷達,因其脈沖重復頻率(pulse repetition frequency, PRF)較大,故在一個CPI內目標通常被認為是相對靜止的,即在M個慢時間內每個目標的散射系數、雙程時延和多普勒頻移均保持不變。因此,假設雷達天線主瓣內存在Q個不同多普勒頻率的目標,則第m個脈沖接收到的回波信號可表示為
Tm(t)=s-m(t)∑Qq=1αTqej2π(m-1)fTqu(t-(m-1)Tr-τqd)(5)
式中:τqd和αTq分別為第q個目標的雷達回波的延時和散射系數;fTq=2vTqTr/λ為第q個目標的歸一化多普勒頻率;vTq為目標速度;λ為雷達工作波長。
由于DRFM干擾機一般需要若干個PRI來捕獲、分析和識別雷達脈沖信號,然后復制這些脈沖并調制多個多普勒信息形成干擾信號,因此干擾信號通常會滯后于回波信號。如圖2所示,假設DRFM干擾機發射脈沖信號滯后雷達發射脈沖信號i(1lt;i≤M)個PRI,則干擾信號回波可表示為
Jm(t)=s-m-i(t)∑Pp=1αJpej2π(m-i-1)fJp·
u(t-(m-i-1)Tr-τpJ)(6)
式中:τpJ、αJp和fJp分別為第p個干擾信號的時延、散射系數和歸一化多普勒頻率。
因此,第m個脈沖的接收回波表示為
ym(t)=Tm(t)+Jm(t)+nm(t)(7)
式中:nm(t)表示高斯白噪聲。
假設雷達接收端對第m個脈沖的信號,采用的濾波器為h-m,其表示為
h-m(t)=∑Nn=1hm(n)u-
t-(n-1)TpTp(8)
式中:hm=[hm(1),hm(2),…,hm(N)]T∈CN為第m個濾波器的復碼字序列。
為了簡化模型,假設所有假目標與真實目標均處于同一距離單元內,即τ1d=τ2d=…=τQd=τ1J=τ2J=…=τPJ=τ0。則經過濾波器后,第m個脈沖在τ0處的輸出為
y(m)=∫+∞-∞h-*m(t-τ0)ym(t)dt=
hHmsm∑Qq=1αTqej2π(m-1)fTq+hHmsm-i∑Pp=1αJpej2π(m-i-1)fJp+v(m)=
x(m)∑Qq=1αTqej2π(m-1)fTq+x-(m)∑Pp=1αJpej2π(m-i-1)fJp+v(m)(9)
式中:x(m)=hHmsm;x-(m)=hHmsm-i;v(m)是方差為σ2的高斯白噪聲;(·)*表示取共軛操作。
2 發射波形與濾波器聯合設計抗速度欺騙干擾
為了抵抗速度欺騙干擾,本文在真實目標頻率附近設置阻帶,通過聯合設計發射波形和濾波器的方法,盡量降低阻帶范圍內的干擾能量和真實目標旁瓣能量,從而提高阻帶內目標的信干噪比和峰值旁瓣比,改善雷達抗速度欺騙干擾性能。
2.1 問題模型
在雷達感知偵察階段,本文利用多通道處理技術[13]獲取干擾滯后真實目標的脈沖重復時間(pulse repetition time, PRT)個數i和真實目標與虛假目標的多普勒信息,然后利用這些先驗信息,雷達系統在目標多普勒附近確定阻帶邊界,確保所有真實目標與虛假目標的多普勒均在阻帶范圍內。假設阻帶范圍為
Ω=∪Nsk=1[fk1,fk2](10)
式中:Ns(Ns≤Q)為阻帶個數;fk1,fk2分別為第k(k=1,2,…,Ns)個阻帶的頻率下限和上限;∪表示取并集。
根據文獻[21],假目標信號經過濾波器輸出后,再做離散傅里葉變換并計算其在阻帶內的頻域能量,則可以推導出P個干擾信號在阻帶內的頻域總能量為
CJ=x-HRJx-(11)
式中:x-=[x-(1),x-(2),…,x-(M)]T。矩陣RJ的第(m,n)個元素表示為
RJ(m,n)=∑Nsk=1∑Pp=1|αJp|2e-j2π(m-n)fJp∫fk2fk1ej2πf(m-n)df=
∑Nsk=1∑Pp=1|αJp|2ej2π(fk2-fJp)(m-n)-ej2π(fk1-fJp)(m-n)j2π(m-n), m≠n
fk2-fk1, m=n(12)
式中:j表示虛數單位。
類似地,Q個目標信號在阻帶內的旁瓣總能量為
CT=xH(RT1+RT2)x=xHRTx(13)
式中:x=[x(1),x(2),…,x(M)]T;(·)H表示共軛轉置操作。RT1和RT2中的第(m,n)個元素分別為
RT1(m,n)=∑Nsk=1∑Qq=1|αTq|2e-j2π(m-n)fTq∫fTq-Δffk1ej2πf(m-n)df=
∑Nsk=1∑Qq=1|αTq|2ej2π(-Δf)(m-n)-ej2π(fk1-fTq)(m-n)j2π(m-n), m≠n
fTq-Δf-fk1, m=n(14)
RT2(m,n)=∑Nsk=1∑Qq=1|αTq|2e-j2π(m-n)fTq∫fk2fTq+Δfej2πf(m-n)df=
∑Nsk=1∑Qq=1|αTq|2ej2π(fk2-fTq)(m-n)-ej2πΔf(i-j)j2π(m-n), m≠n
fk2-fTq-Δf, m=n(15)
式中:Δf=1/M為歸一化多普勒頻率間隔。
構造分塊矩陣H和S,定義為
再構造長序列s^和h^為
s^=[sT1, sT2, …, sTM]TNM×1(18)
h^=[hH1, hH2, …, hHM]TNM×1(19)
則有
x=HHs^=SHh^
x-=HH(J1s^)=(J2SHJH1)h^(20)
式中:J1,J2為移位矩陣,定義為
J1=0iN×N(M-i)INi×Ni
IN(M-i)×N(M-i)0N(M-i)×NiNM×NM(21)
J2=0i×(M-i)Ii×i
I(M-i)×(M-i)0(M-i)×iM×M(22)
因此有:
CJ=x-HRJx-=s^H(JH1HRJHHJ1)s^=h^H(J1SJH2RJJ2SHJH1)h^(23)
CT=xHRTx=s^H(HRTHH)s^=h^H(SRTSH)h^(24)
為了抗速度欺騙干擾,需最小化阻帶內干擾信號能量和目標信號旁瓣能量。此外,由于考慮了發射波形和接收濾波器聯合設計,相比匹配濾波體制,不可避免地將造成信噪比的損失,因此在聯合設計過程中,基于罰函數的方法,引入了峰值約束,即最小化目標函數為
f(s^,h^)=ω1s^H(JH1HRJHHJ1)s^+ω2s^H(HRTHH)s^+
λ|h^Ts^-amax|2=ω1h^H(J1SJH2RJJ2SHJH1)h^+
ω2h^H(SRTSH)h^+λ|h^Ts^-amax|2(25)
其中,懲罰參數λ的目的是對目標函數|h^Ts^-amax|2施加懲罰,從而迫使生成波形非匹配濾波輸出峰值趨近于預設值amax。當λ取值越大,表示施加懲罰力度越大,則設計波形非匹配濾波輸出值越接近于預設值。當λ取值越小,表示施加懲罰力度越小,則設計波形非匹配濾波輸出值與預設值相差越大。為了綜合考慮設計波形的抗速度欺騙干擾性能和脈壓峰值損失,需合理選取懲罰參數λ。ω1,ω2分別為目標旁瓣能量和干擾能量的權重因子,用于控制優化目標旁瓣能量和干擾能量的優先度,且有ω1+ω2=1。
此外,為了避免發射波形過功率放大器時發生非線性失真,對于發射波形考慮了能量約束和PAPR約束,并對接收濾波器考慮恒能量約束。PAPR定義為
PAPR(sm)=maxn|sm(n)|21N∑Nn=1|sm(n)|2, m=1,2,…,M(26)
綜上所述,發射波形與濾波器聯合設計抗速度欺騙干擾優化問題可表示為
mins^,h^ f(s^,h^)
s.t. PAPR(sm)≤γ
sHmsm=N
hHmhm=N
m=1,2,…,M(27)
式中:γ為預設的PAPR閾值。
2.2 算法求解
顯然式(27)中的優化問題是非凸的,同時求解發射波形和濾波器是非常困難的。因此,本文基于塊坐標下降法(block coordinate descent, BCD)算法的思想,對發射波形和濾波器進行交替迭代優化求解。BCD算法原理如下:
初始化變量s^(0),h^(0),在迭代中分別固定其中一個變量,再優化另一個變量,即重復以下迭代
s^(k)=arg mins^ f(s^,h^(k-1))
h^(k)=arg minh^ f(s^(k),h^)(28)
式中:k=1,2,…,k,k表示算法總迭代次數;s^(k)和h^(k)分別函數f(s^,h^(k-1))和f(s^(k),h^)的最優值。因此,有
f(s^(K),h^(K))…≤f(s^(k),h^(k))≤f(s^(k),h^(k-1))≤
f(s^(k-1),h^(k-1))≤…≤f(s^(0),h^(0))(29)
從式(29)可以看出,BCD算法能夠保證目標函數值單調遞減至收斂。
因此,基于BCD算法原理,將式(27)中的優化問題分解為如下兩個子問題:
首先,考慮固定接收濾波器條件下,對雷達發射波形進行優化求解,即優化問題式(30)。根據式(27),可以將優化問題簡寫為
mins^ s^HPs^-2amaxλR(s^Hh^*)
s.t.PAPR(sm)≤γ
sHmsm=N, m=1,2,…,M(32)
式中:R(·)表示取實部操作,
P=ω1(JHHRJHHJ)+ω2(HRTHH)+λh^*h^T(33)
對于式(32)中優化問題可利用優化最小化(majorization-minimization, MM)方法進行求解,且由于矩陣P為厄米特矩陣,根據文獻[22]中引理1,式(32)中優化問題可轉化為
mins^ R(s^H(P-tr(P)INM)s^(l))-amaxλR(s^Hh^*)
s.t.PAPR(sm)≤γ
sHmsm=N, m=1,2,…,M(34)
式中:s^(l)表示第l次迭代下的波形;INM表示NM階的單位陣。為了避免計算tr(P)帶來的額外計算量,下面引理1中,給出了tr(P)的顯示表達式。
引理1 假設一個定義為式(33)的矩陣P,則它的跡為
tr(P)=ω1N·tr(RJ)+ω2N·tr(RT)+λNM(35)
證明 由tr(A+B)=tr(A)+tr(B),有
tr(P)=tr(ω1(JHHRJHHJ))+tr(ω2(HRTHH))+
tr(λh^*h^T)=∑Mm=1(ω1RJ(m,m)hHmhm+
ω2RT(m,m)hHmhm+λhHmhm)=
ω1N·tr(RJ)+ω2N·tr(RT)+λNM(36)
式中:RJ(m,m)和RT(m,m)分別表示矩陣RJ和RT的第(m,m)個元素。證畢
由問題式(34)等價于
mins^ s^-y2
s.t.PAPR(sm)≤γ
sHmsm=N
m=1,2,…,M(37)
式中:y=-((P-Tr(P)INM)s^(l)-amaxλh^*)。
根據文獻[22],首先令
bm=Nymym, m=1,2,…,M(38)
式中:ym表示向量y的第(m-1)N+1個到第mN個元素,即有y=[yT1,yT2,…,yTM]T。則式(37)的最優解為
s(l+1)m=bm, maxn|bm(n)|≤γ
b^m, 其他, m=1,2,…,M(39)
式中:b^m求解步驟如下。
步驟 1 設置b^m=bm,指標集={1,2…,N},k=1;
步驟 2 如果maxn|bm(n)|gt;γ;
步驟 3 令yα=maxn|ym(n)|,p∈為yα的位置;
步驟 4 b^m(p)=γejarg(yα);
步驟 5 =-p;
步驟 6 b^m()=N-kγym()ym();
步驟 7 k=k+1;
步驟 8 結束。
接下來考慮固定發射波形條件下,對接收濾波器進行優化求解。與求解發射波形類似地,優化問題式(31)可寫為
minh^ h^HQh^-2amaxλR(h^Hs^*)
s.t. hHmhm=N
m=1,2,…,M(40)
式中:
Q=ω1(JSJHRJJSHJH)+ω2(SRTSH)+λh^*h^T(41)
由于矩陣Q為厄米特矩陣,則采用MM算法可等價于下式優化問題:
minh^ R(h^H(Q-Tr(Q)INM)h^(l))-amaxλR(h^Hs^*)
s.t. hHmhm=N
m=1,2,…,M(42)
與引理1類似,可以證明tr(Q)=ω1N·tr(RJ)+ω2N·tr(RT)+λNM。
顯然,式(42)為二次約束的線性優化問題,利用拉格朗日數乘法可得到其最優解為
h(l+1)m=Nv*mvm, m=1,2,…,M(43)
式中:v=-((Q-Tr(Q)INM)h^(l)-amaxλs^*);vm為v中第(m-1)N+1到第mN個元素。
綜上所述,本文將發射波形與接收濾波器聯合設計問題,轉化為發射波形設計與接收濾波器設計兩個子問題,再采用BCD的思想交替優化,且每次迭代中均采用MM算法框架進行求解,根據BCD與MM算法原理[23],可知本文提出算法是單調且收斂的。本文將上述算法命名為BCD-MM(block coordinate descent majorization minimization),算法主要步驟總結如下,設置停止迭代條件為
epsilon=s^(l+1)-s^(l)+h^(l+1)-h^(l)≤ε(44)
式中:ε為收斂閾值,通過多次實驗綜合考慮算法性能與搜索時間得出,通常設置為ε=10-5。在迭代過程中,為進一步提高算法收斂速度,可以采用文獻[24]提出的基于平方迭代法(squared iterative method, SIM) 的加速方案。
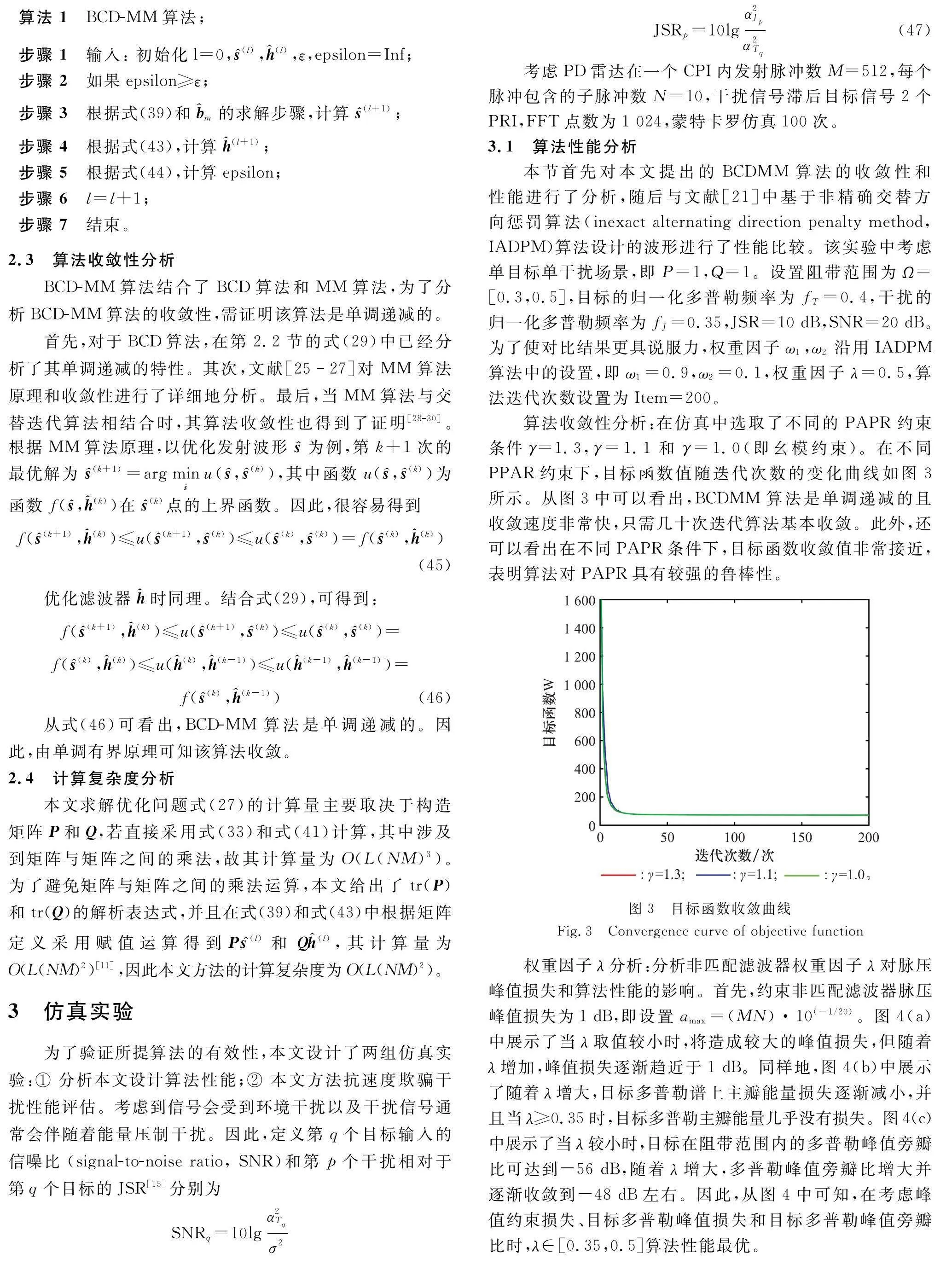
算法 1 BCD-MM算法;步驟 1 輸入: 初始化l=0,s^(l),h^(l),ε,epsilon=Inf;
步驟 2 如果epsilon≥ε;
步驟 3 根據式(39)和b^m的求解步驟,計算s^(l+1);
步驟 4 根據式(43),計算h^(l+1);
步驟 5 根據式(44),計算epsilon;
步驟 6 l=l+1;
步驟 7 結束。2.3 算法收斂性分析
BCD-MM算法結合了BCD算法和MM算法,為了分析BCD-MM算法的收斂性,需證明該算法是單調遞減的。
首先,對于BCD算法,在第2.2節的式(29)中已經分析了其單調遞減的特性。其次,文獻[25-27]對MM算法原理和收斂性進行了詳細地分析。最后,當MM算法與交替迭代算法相結合時,其算法收斂性也得到了證明[28-30]。根據MM算法原理,以優化發射波形s^為例,第k+1次的最優解為s^(k+1)=argmins^ u(s^,s^(k)),其中函數u(s^,s^(k))為函數f(s^,h^(k))在s^(k)點的上界函數。因此,很容易得到
f(s^(k+1),h^(k))≤u(s^(k+1),s^(k))≤u(s^(k),s^(k))=f(s^(k),h^(k))(45)
優化濾波器h^時同理。結合式(29),可得到:
f(s^(k+1),h^(k))≤u(s^(k+1),s^(k))≤u(s^(k),s^(k))=
f(s^(k),h^(k))≤u(h^(k),h^(k-1))≤u(h^(k-1),h^(k-1))=
f(s^(k),h^(k-1))(46)
從式(46)可看出,BCD-MM算法是單調遞減的。因此,由單調有界原理可知該算法收斂。
2.4 計算復雜度分析
本文求解優化問題式(27)的計算量主要取決于構造矩陣P和Q,若直接采用式(33)和式(41)計算,其中涉及到矩陣與矩陣之間的乘法,故其計算量為O(L(NM)3)。為了避免矩陣與矩陣之間的乘法運算,本文給出了tr(P)和tr(Q)的解析表達式,并且在式(39)和式(43)中根據矩陣定義采用賦值運算得到Ps^(l)和Qh^(l),其計算量為O(L(NM)2)[11],因此本文方法的計算復雜度為O(L(NM)2)。
3 仿真實驗
為了驗證所提算法的有效性,本文設計了兩組仿真實驗:① 分析本文設計算法性能;② 本文方法抗速度欺騙干擾性能評估。考慮到信號會受到環境干擾以及干擾信號通常會伴隨著能量壓制干擾。因此,定義第q個目標輸入的信噪比 (signal-to-noise ratio, SNR)和第p個干擾相對于第q個目標的JSR[15]分別為
SNRq=10lgα2Tqσ2
JSRp=10lgα2Jpα2Tq(47)
考慮PD雷達在一個CPI內發射脈沖數M=512,每個脈沖包含的子脈沖數N=10,干擾信號滯后目標信號2個PRI,FFT點數為1 024,蒙特卡羅仿真100次。
3.1 算法性能分析
本節首先對本文提出的BCDMM算法的收斂性和性能進行了分析,隨后與文獻[21]中基于非精確交替方向懲罰算法(inexact alternating direction penalty method, IADPM)算法設計的波形進行了性能比較。該實驗中考慮單目標單干擾場景,即P=1,Q=1。設置阻帶范圍為Ω=[0.3,0.5],目標的歸一化多普勒頻率為fT=0.4,干擾的歸一化多普勒頻率為fJ=0.35,JSR=10 dB,SNR=20 dB。 為了使對比結果更具說服力,權重因子ω1,ω2沿用IADPM算法中的設置,即ω1=0.9,ω2=0.1,權重因子λ=0.5,算法迭代次數設置為Item=200。
算法收斂性分析:在仿真中選取了不同的PAPR約束條件γ=1.3,γ=1.1和γ=1.0(即幺模約束)。在不同PPAR約束下,目標函數值隨迭代次數的變化曲線如圖3所示。從圖3中可以看出,BCDMM算法是單調遞減的且收斂速度非常快,只需幾十次迭代算法基本收斂。此外,還可以看出在不同PAPR條件下,目標函數收斂值非常接近,表明算法對PAPR具有較強的魯棒性。
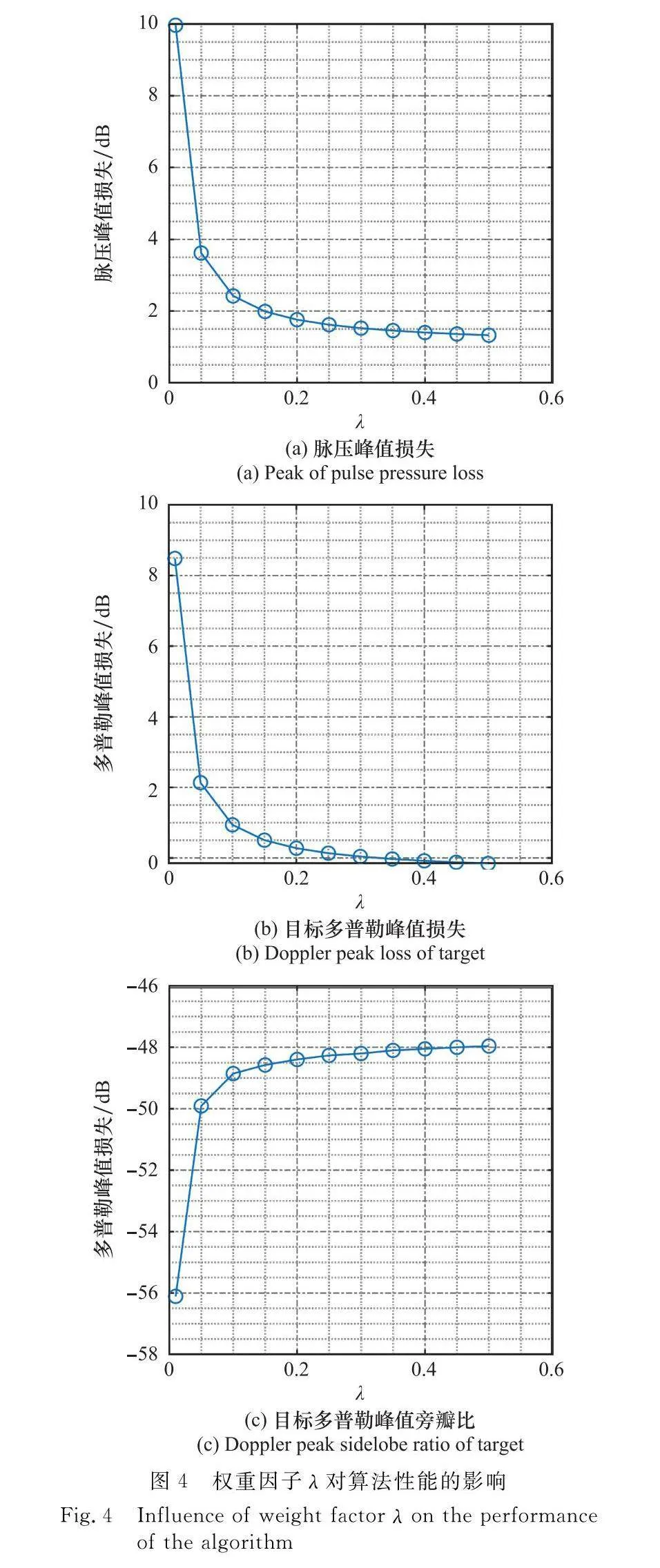
權重因子λ分析:分析非匹配濾波器權重因子λ對脈壓峰值損失和算法性能的影響。首先,約束非匹配濾波器脈壓峰值損失為1 dB,即設置amax=(MN)·10(-1/20)。圖4(a)中展示了當λ取值較小時,將造成較大的峰值損失,但隨著λ增加,峰值損失逐漸趨近于1 dB。同樣地,圖4(b)中展示了隨著λ增大,目標多普勒譜上主瓣能量損失逐漸減小,并且當λ≥0.35時,目標多普勒主瓣能量幾乎沒有損失。圖4(c)中展示了當λ較小時,目標在阻帶范圍內的多普勒峰值旁瓣比可達到-56 dB,隨著λ增大,多普勒峰值旁瓣比增大并逐漸收斂到-48 dB左右。因此,從圖4中可知,在考慮峰值約束損失、目標多普勒峰值損失和目標多普勒峰值旁瓣比時,λ∈[0.35,0.5]算法性能最優。
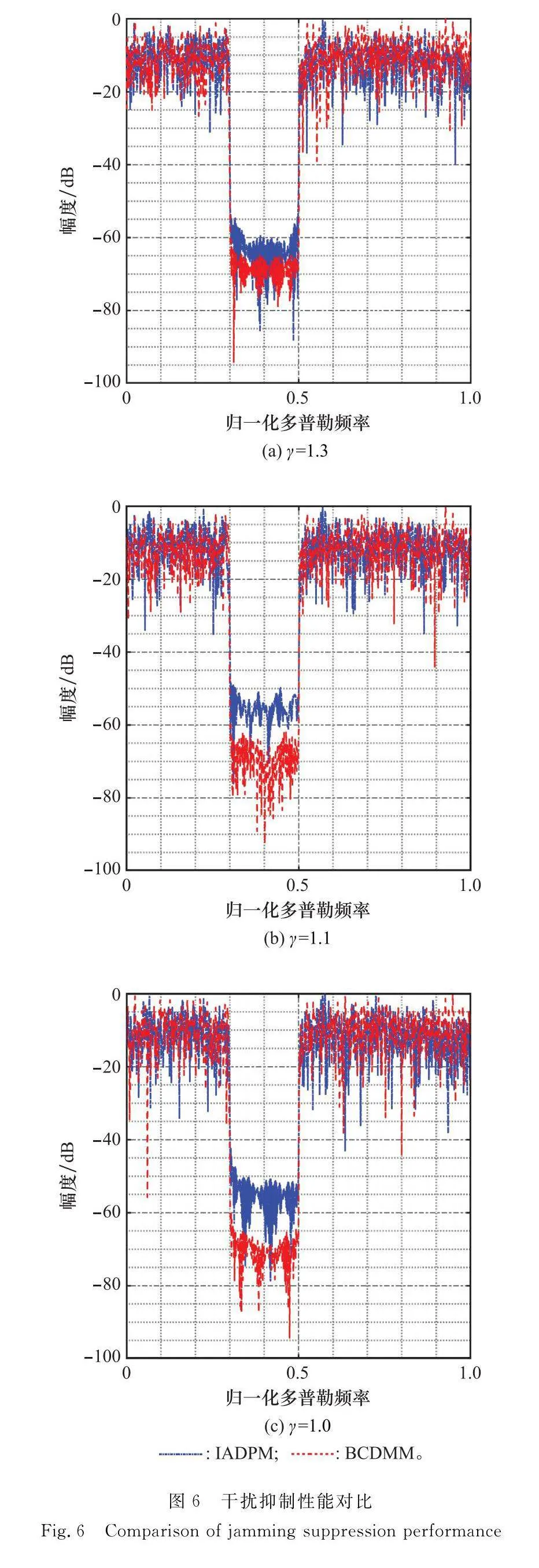
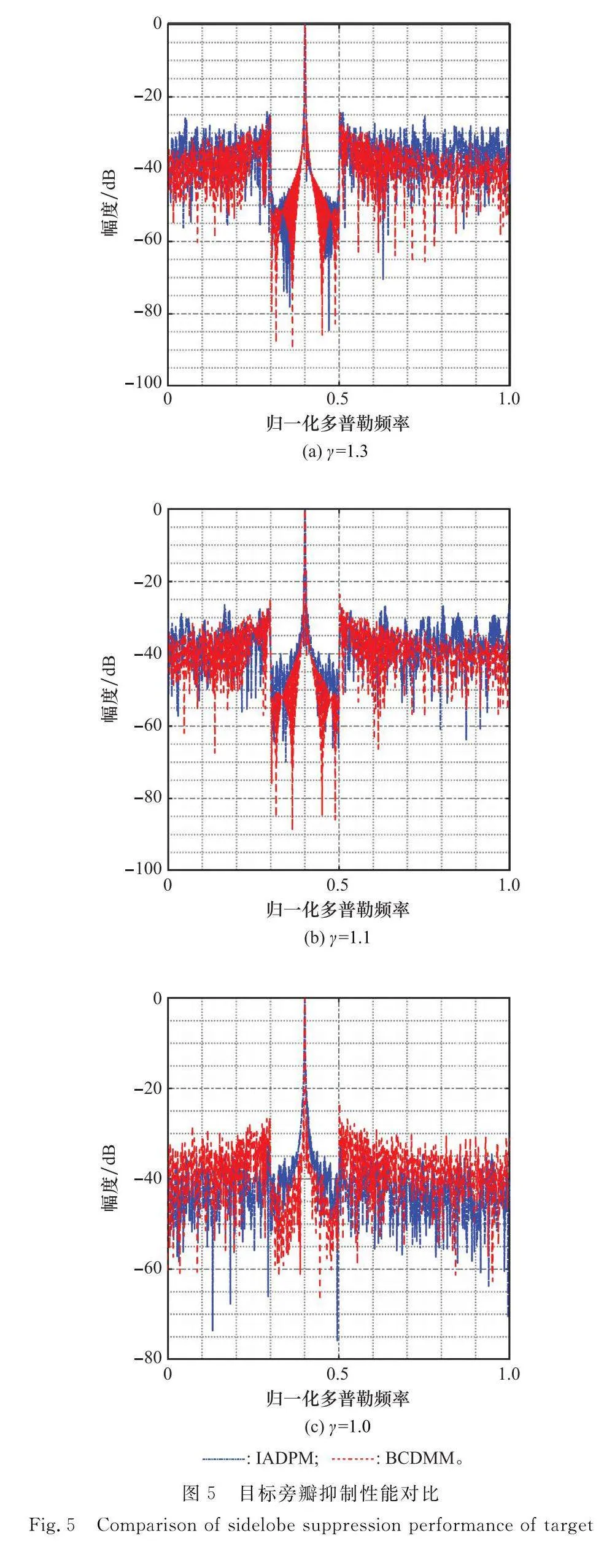
與已有工作性能對比分析:針對γ=1.3,γ=1.1和γ=1.0共3個不同PAPR約束下,分別比較了本文算法和IADPM算法設計波形在多普勒譜上對目標旁瓣和干擾的抑制性能法相比BCD-MM算法設計波形在阻帶范圍內的峰值旁瓣比更大。圖5中展示了在不同的PAPR約束下,本文算法設計波形對目標旁瓣均有較好的抑制性能,而IADPM算法設計波形的目標旁瓣性能隨著PAPR的降低而減弱。尤其是當γ=1.0時,IADPM算法退化為脈間初相設計,無法對目標旁瓣進行優化,但是本文設計算法在該場景下依舊有效,且目標旁瓣區域出現明顯的凹槽。圖6中展示出了在不同PAPR約束下,本文算法設計波形的干擾能量均大約為-65 dB,明顯優于IADPM,尤其在γ=1.0時,性能提升更大。
3.2 抗干擾效果分析
本節首先在單目標單干擾場景下,對比分析了BCD-MM算法和IADPM算法設計波形的抗干擾性能以及對SNR和JSR的魯棒性。隨后,再分析了其在多目標多干擾場景下的抗干擾性能。
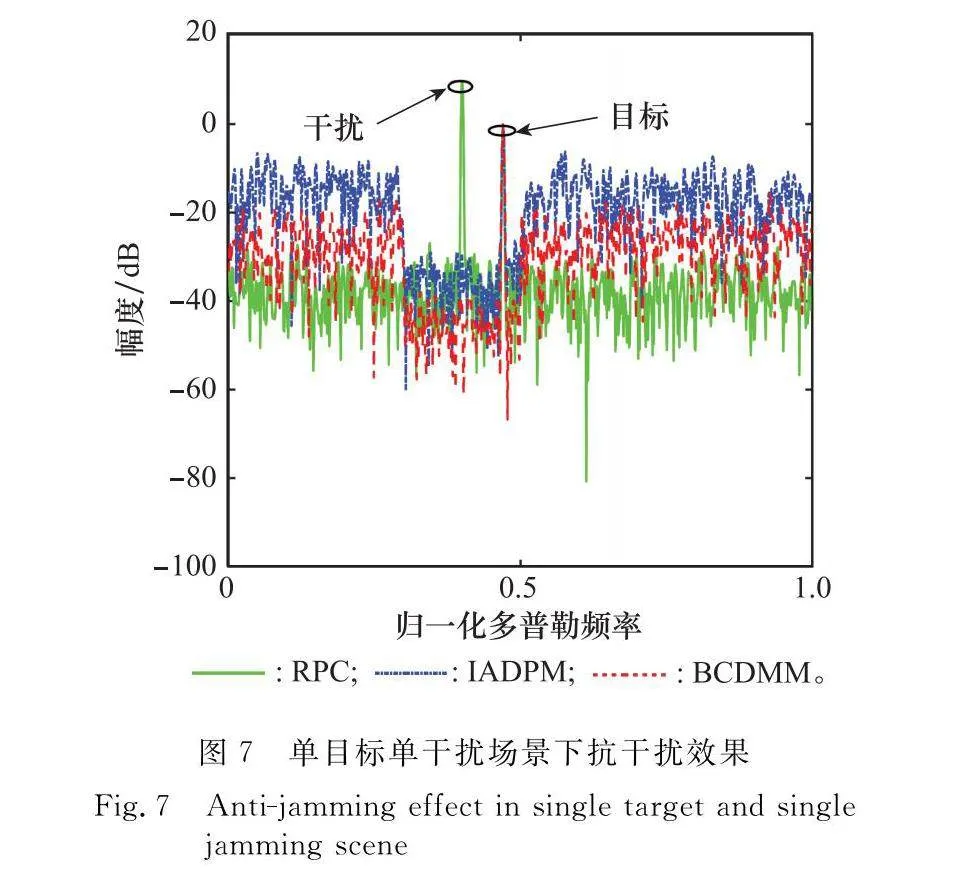
抗單干擾性能分析:在單目標單干擾場景下,對比分析BCD-MM算法設計波形、IADPM算法設計波形和隨機相位編碼RPC波形的抗干擾性能。首先,設置γ=1.1,SNR=20 dB,JSR=10 dB,其他參數與第3.1節保持一致,仿真過程中采用Hamming窗。從圖7中可以看出,當雷達每個脈沖都發射固定的隨機相位編碼波形且接收端采用匹配濾波時,雷達接收信號多普勒譜上將出現干擾和目標兩個尖峰,且干擾具有更高的能量,因此雷達系統將會遭受嚴重的速度欺騙干擾。而采用IADPM算法設計和本文算法設計波形時,雷達接收信號的多普勒譜在阻帶范圍內有一個明顯的凹槽且只有目標一個峰值,表明雷達系統具有較強的抗速度欺騙干擾能力,能夠準確地識別目標。此外,與IADPM相比,采用BCD-MM算法設計波形時,目標的峰值旁瓣比提升將近6 dB,表明本文算法設計波形具有更強的抗速度欺騙干擾性能。
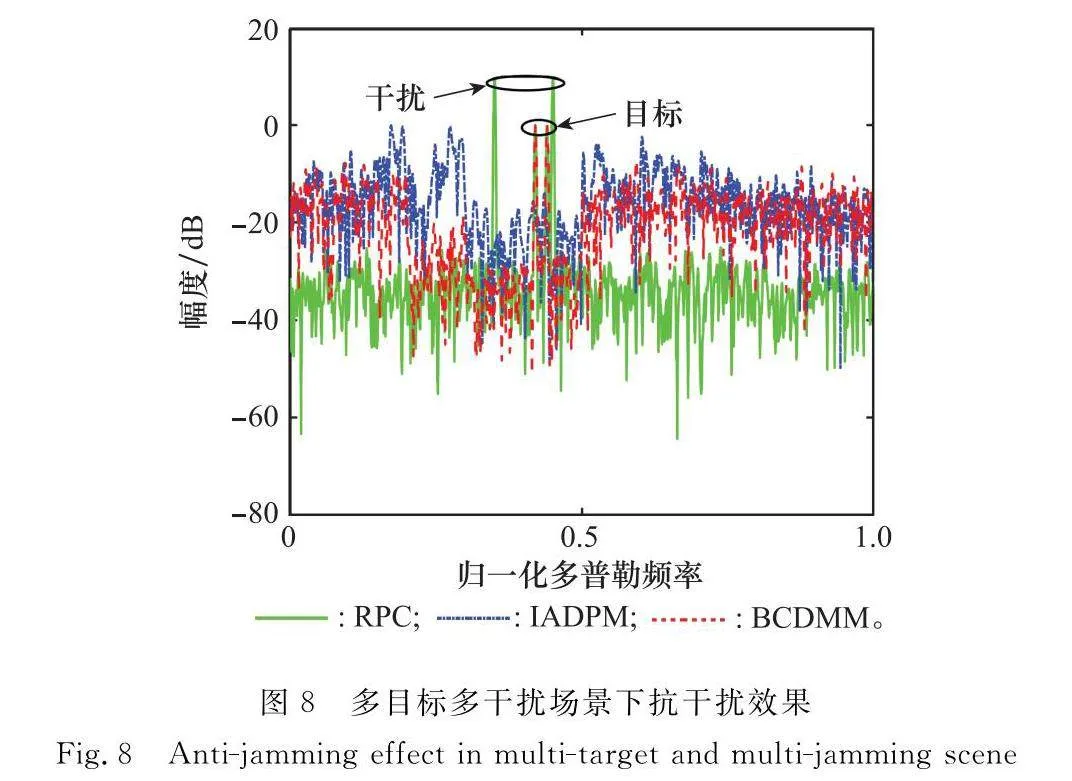
抗多干擾性能分析:在多目標與多干擾場景下,對比分析BCD-MM算法設計波形、IADPM算法設計波形和RPC波形的抗干擾性能。假設P=2,Q=2,目標信號歸一化多普勒頻率為fT1=0.42,fT2=0.44,干擾信號的歸一化多普勒頻率為fJ1=0.35,fJ2=0.45,SNR=20 dB,JSR1=JSR2=10 dB,γ=1.1,其他參數與第3.1節保持一致。
從圖8中可以看出,在阻帶范圍內,采用固定RPC波形和匹配濾波得到的多普勒譜中同時出現了兩個干擾信號和兩個目標信號,且干擾信號的峰值高于目標信號,將造成雷達系統誤檢;而采用IADPM算法設計波形與本文設計波形時,得到的多普勒譜在阻帶范圍中,干擾目標被抑制,雷達系統能夠準確地進行目標檢測。與IADPM算法設計波形相比,采用本文算法設計波形的接收信號旁瓣更低,有更大的峰值旁瓣比,即抗干擾能力更強。
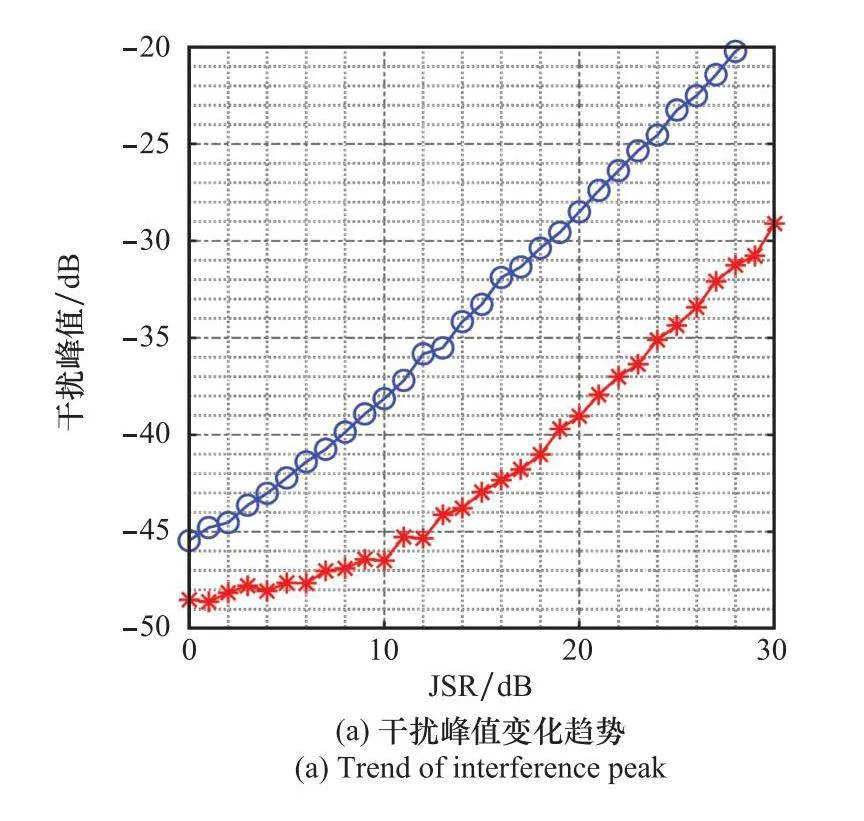
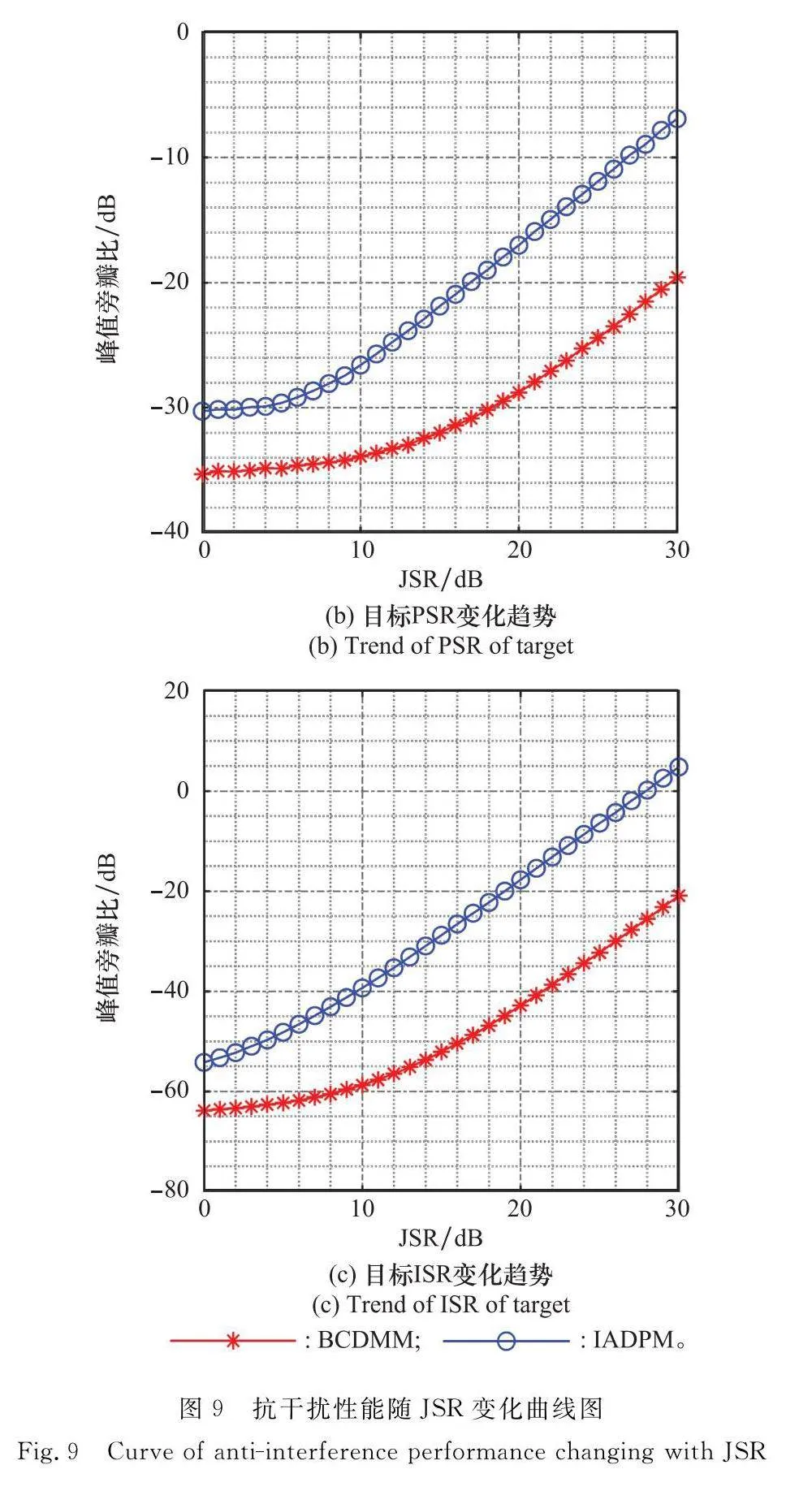
JSR魯棒性分析:在單目標單干擾場景下,對比分析IADPM算法設計和BCDMM算法設計波形的抗干擾性能隨JSR的變化趨勢。設置SNR=20 dB,其他參數不變。圖9(a)展示了干擾峰值隨JSR的變化趨勢,干擾峰值越小表明設計波形的抑制干擾能力越強。從圖9(a)中可以看出,采用IADPM算法設計波形與BCD-MM算法設計波形都具有較強的干擾抑制能力,即使JSR=30 dB,干擾峰值依然被抑制在-17 dB以下,尤其是采用BCD-MM設計波形時,干擾峰值被抑制在-28 dB左右。由于干擾的多普勒能量將分散到整個多普勒譜上從而導致目標的峰值旁瓣比降低,圖9(b)和圖9(c)分別展示目標峰值旁瓣比(peak sidelobe ratio, PSR)和積分旁瓣比(integrated sidelobe ratio, ISR)[31]隨JSR的變化趨勢。從中可以看出,隨著JSR增大,BCD-MM算法設計波形的始終有較大的PSR和ISR,且均優于IADPM算法設計波形。
4 結束語
本文綜合考慮了脈內、脈間和接收濾波器多個自由度,研究了一種雷達發射波形和非匹配濾波器聯合設計抗速度欺騙干擾方法,并提出一個基于BCD法和MM法的交替迭代算法BCD-MM。此外,理論分析了算法的計算復雜度為O(L(MN)2)。仿真實驗表明,在單干擾和多干擾場景下,本文方法均能夠有效地抑制速度欺騙干擾。與傳統采用脈間編碼設計波形相比,本文設計波形的抗速度干擾性能提升了大約為6 dB,且在強噪聲或強干擾條件下,依舊具有較好的抗速度欺騙干擾效果。本文提出算法中結合了BCD和MM算法原理,雖然保證了算法的收斂性,但是與BCD算法類似地存在容易陷入局部最優的問題,未來工作中可將文中雙變量優化問題轉化為單變量優化問題來避免該問題。
參考文獻
[1]趙國慶. 雷達對抗原理[M]. 2版. 西安: 西安電子科技大學出版社, 2012.
ZHAO G Q. Principle of radar countermeasure[M]. 2nd ed. Xi’an: Xidian University Press, 2012.
[2]盧剛. 雷達有源假目標抑制方法研究[D]. 成都: 電子科技大學, 2012.
LU G. Study of algorithms on suppression of radar active 1 targets[D]. Chengdu: University of Electronic Science and Technology of China, 2012.
[3]AUBRY A, MAIO A D, JIANG B, et al. Ambiguity function shaping for cognitive radar via complex quartic optimization[J]. IEEE Trans.on Signal Processing, 2013, 61(22): 5603-5619.
[4]JIU B, LIU H W, ZHANG L, et al. Wideband cognitive radar waveform optimization for joint target radar signature estimation and target detection[J]. IEEE Trans.on Aerospace and Electronic Systems, 2015, 51(2): 1530-1546.
[5]SOUMEKH M. SAR-ECCM using phase-perturbed LFM chirp signals and DRFM repeat jammer penalization[J]. IEEE Trans.on Aerospace and Electronic Systems, 2006, 42(1): 191-205.
[6]AKHTAR J. An ECCM scheme for orthogonal independent range-focusing of real and 1 targets[C]∥Proc.of the IEEE Radar Conference, 2007: 846-849.
[7]AKHTAR J. Orthogonal block coded ECCM schemes against repeat radar jammers[J]. IEEE Trans.on Aerospace and Electronic Systems, 2009, 45(3): 1218-1226.
[8]ZHOU K, LI D X, QUAN S N, et al. SAR waveform and mismatched filter design for countering interrupted-sampling repeater jamming[J]. IEEE Trans.on Geoscience and Remote Sensing, 2021, 60: 5214514.
[9]周凱, 何峰, 粟毅. 一種快速抗間歇采樣轉發干擾波形和濾波器聯合設計算法[J]. 雷達學報, 2022, 11(2): 264-277.
ZHOU K, HE F, SU Y. Fast algorithm for joint waveform and filter design against interrupted sampling repeater jamming[J]. Journal of Radars, 2022, 11(2): 264-277.
[10]周凱, 李德鑫, 粟毅, 等. 基于雷達發射波形和非匹配濾波聯合設計的間歇采樣轉發干擾抑制方法[J]. 電子與信息學報, 2021, 43(7): 1939-1946.
ZHOU K, LI D X, SU Y, et al. Joint transmitted waveform and mismatched filter design against interrupted-sampling repeater jamming[J]. Journal of Electronics amp; Information Technology, 2021, 43(7): 1939-1946.
[11]王福來, 龐晨, 殷加鵬, 等. 一種多普勒容忍的抗間歇采樣轉發干擾恒模互補波形和接收濾波器聯合設計方法[J]. 雷達學報, 2022, 11(2): 278-288.
WANG F L, PANG C, YIN J P, et al. Joint design of Doppler-tolerant complementary sequences and receiving filters against interrupted sampling repeater jamming[J]. Journal of Radars, 2022, 11(2): 278-288.
[12]ZHENG H, JIU B, LIU H. Waveform design based ECCM scheme against interrupted sampling repeater jamming for wideband MIMO radar in multiple targets scenario[J]. IEEE Sensors Journal, 2022, 22(2): 1652-1669.
[13]GONG S X, WEI X Z, LI X. ECCM scheme against interrupted sampling repeater jammer based on time-frequency analysis[J]. Journal of Systems Engineering and Electronics, 2014, 25(6): 996-1003.
[14]LIN K. Anti-jamming MTI radar using variable pulse-codes[D]. Massachusetts: Massachusetts Institute of Technology, 2002.
[15]ZHANG J D, ZHU D Y, ZHANG G. New anti-velocity deception jamming technique using pulses with adaptive initial phases[J]. IEEE Trans.on Aerospace and Electronic Systems, 2013, 49(2): 1290-1300.
[16]YANG Y, WU J, CUI G L, et al. Optimized phase-coded waveform design against velocity deception[C]∥Proc.of the IEEE Radar Conference. 2015: 400-404.
[17]CUI G L, JI H M, CAROTENUTO V, et al. An adaptive sequential estimation algorithm for velocity jamming suppression[J]. Signal Processing, 2017, 134: 70-75.
[18]吳健, 崔國龍, 孔令講. 一種抗速度欺騙干擾的認知波形設計方法[J]. 雷達科學與技術, 2015, 13(2): 133-138.
WU J, CUI G L, KONG L J. A cognitive waveform design approach against velocity deception jamming[J]. Radar Science and Technology, 2015, 13(2): 133-138.
[19]XIONG W, WANG X H, ZHANG G. Cognitive waveform design for anti-velocity deception jamming with adaptive initial phases[C]∥Proc.of the IEEE Radar Conference, 2016.
[20]ZHANG S, YANG Y, CUI G L, et al. Range-velocity jamming suppression algorithm based on adaptive iterative filtering[C]∥Proc.of the IEEE Radar Conference, 2016.
[21]葛萌萌, 余顯祥, 嚴正欣, 等. 脈間波形幅相聯合設計抗欺騙干擾方法[J]. 電子科技大學學報, 2021, 50(4): 481-487.
GE M M, YU X X, YAN Z X, et. al. Optimized amplitude-phase waveform against deceptive jamming[J]. Journal of University of Electronic Science and Technology of China, 2021, 50(4): 481-487.
[22]TROPP J, DHILLON I, HEATH R, et al. Designing structured tight frames via an alternating projection method[J]. IEEE Trans.on Information Theory, 2005, 51(1):188-209.
[23]王佳歡, 范平志, 時巧, 等. 一種具有多普勒容忍性的通感一體化波形設計[J]. 雷達學報, 2023, 12(2):275-286.
WANG J H, FAN P Z, SHI Q, et. al. Doppler resilient integrated sensing and communication waveforms design[J]. Journal of Radars, 2022, 12(2):275-286.
[24]SONG J X, BABU P, PALOMAR D P. Optimization methods for designing sequences with low autocorrelation sidelobes[J]. IEEE Trans.on Signal Processing, 2015, 63(15):3998-4009.
[25]SUN Y, BABU P, PALOMAR D P. Majorization-minimization algorithms in signal processing, communications, and machine learning[J]. IEEE Trans.on Signal Processing, 2017, 65(3): 794-816.
[26]BOLTE J, SABACH S, TEBOULLE M. Proximal alternating linearized minimization for nonconvex and nonsmooth problems[J]. Mathematical Programming, 2014, 146(1/2): 459-494.
[27]GEIPING J, MOELLER M. Composite optimization by nonconvex majorization-minimization[J]. SIAM Journal on Imaging Sciences, 2018, 11(4): 2494-2528.
[28]LIANG J L, SO H C, LI J, et al. Unimodular sequence design based on alternating direction method of multipliers[J]. IEEE Trans.on Signal Processing, 2016, 64(20): 5367-5381.
[29]CHANG H B, ENFEDAQUE P, MARCHESINI S, et al. Blind ptychographic phase retrieval via convergent alternating direction method of multipliers[J]. SIAM Journal on Imaging Sciences, 2019, 12(1): 153-185.
[30]ZHOU K, QUAN S N, LI D X, et al. Waveform and filter joint design method for pulse compression sidelobe reduction[J]. IEEE Trans.on Geoscience and Remote Sensing, 2022, 60: 5107615.
[31]時巧. 基于OQAM-OFDM信號的距離旁瓣抑制方法研究[D]. 成都: 電子科技大學, 2022.
SHI Q. Research on range sidelobe suppression method based on OQAM-OFDM signal[D]. Chengdu: University of Electronic Science and Technology of China, 2022.
作者簡介
張明興(1994—),男,博士研究生,主要研究方向為雷達波形設計、雷達抗干擾技術。
時 巧(1991—),女,講師,博士,主要研究方向為雷達波形設計、雷達通信一體化波形設計。
余 濤(1996—),男,博士研究生,主要研究方向為雷達波形設計、雷達抗干擾技術。
周正春(1978—),男,教授,博士,主要研究方向為編碼理論、通信/雷達波形設計、電子信息對抗。
崔國龍(1982—),男,教授,博士,主要研究方向為認知波形設計、陣列信號處理、最優化理論。

