基于壓縮感知的低復雜度超分辨角度估計方法

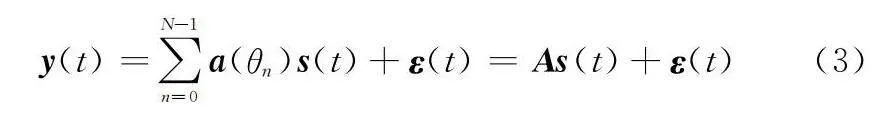
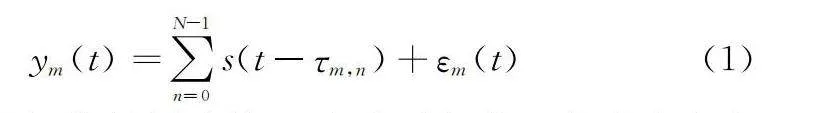
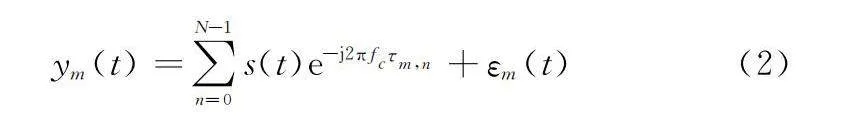
摘要： 在空域目標角度估計中，分辨率受陣列孔徑的限制，依靠增加陣元數量提高分辨率會增加系統成本。為了在受限陣列尺寸中減少陣元數量，基于壓縮感知（compressive sensing， CS）理論，提出了一種超分辨角度估計算法。首先建立陣列接收信號模型并構造冗余字典，然后利用目標空間域稀疏先驗信息將目標角度估計問題建模為優化問題，最后設計低復雜度算法對優化問題求解。所提算法通過貝葉斯CS理論推導了正則化系數，保證了算法的噪聲抑制性能，通過共軛梯度運算及Hadamard乘積提高了算法效率。所提算法可利用較少快拍在信號數目未知的條件下，實現高精度角度估計。仿真結果和實測數據驗證了所提算法的有效性。

關鍵詞： 陣列信號處理; 壓縮感知; 波達方向估計; 波束形成

中圖分類號： TN 911.7

文獻標志碼： A

DOI：10.12305/j.issn.1001-506X.2024.06.01

Low complexity super-resolution angle estimation method based on compressive sensing

WU Min^1，2， LI Zihao^1，2， HAO Chengpeng^1，2，*， HU Qiao³

（1. Institute of Acoustics， Chinese Academy of Sciences， Beijing 100190， China; 2. University of Chinese Academy of Sciences， Beijing 100049， China; 3. School of Mechanical Engineering， Xi’an Jiaotong University， Xi’an 710049， China）

Abstract： In aerial target angle estimation， the resolution is constrained by the aperture length. Increasing the number of array elements to improve the resolution will increase the system lost. To reduce the number of elements in the limited array size， a novel algorithm of super-resolution angle estimation is addressed based on compressive sensing （CS） theory. The array received signal model is established and the redundant dictionary is formed. By exploiting the sparse prior information of the observation area， the target angle estimation problem is converted into the optimization problem. The direction of arrival of targets can be estimated with accuracy via an iterative optimization algorithm. In the proposed algorithm， the regularization coefficient is derived by Bayesian CS theory to ensure the noise robustness of the algorithm. Besides， the efficiency of the proposed algorithm is improved by using the conjugate gradient algorithm and Hadamard product. The effectiveness of the proposed algorithm is verified by simulation and measured data.

Keywords： array signal processing; compressive sensing （CS）; direction of arrival （DOA） estimation; beam forming

0 引 言

隨著聲納技術的高速發展，陣列信號處理可實現對水下目標的高分辨探測和定位，其基本原理是利用陣元傳感器接收各個方向的信號，估計信號的到達方向（direction of arrival， DOA）角是陣列信號處理的重要任務，以獲取信號源的信源數、角度等信息為目的^［1］。常見的DOA估計方法有時延求和（delay-and-sum， DAS）和最小方差無畸變（minimum variance distortion-less response， MVDR）算法。DAS通過補償各通道時延差后求和得到波束輸出，其計算復雜度低，穩健性高，但受孔徑大小的限制，空間分辨率較低。Capon^［2］提出的MVDR波束形成器，采用最小化噪聲方差準則，在感興趣角度無失真輸出的前提下最小化輸出功率，形成空間譜，采用的線性模型對于噪聲的利用率較低，導致算法具有一定的局限性。20世紀70年代末涌現的一些子空間類方法對DOA估計研究具有劃時代意義，其中最具代表性的是多重信號分類（multiple signal classification， MUSIC）算法^［3］。該算法通過對接收數據進行空間分解，將空間劃分為信號子空間和噪聲子空間，利用子空間的正交特性構造出空間譜圖并進行譜峰搜索，從理論上克服了瑞利極限，可獲得目標角度的超分辨估計，但自相關矩陣特征值分解以及譜峰搜索導致算法計算復雜度高。基于旋轉不變的信號參數估計（estimation of signal parameters by rotational invariance techniques， ESPRIT）的子空間類方法^［4］，此算法無需進行譜峰搜索，降低了算法運算量，增加了DOA估計方法的實用性。近年來，學者們在MUSIC算法和ESPRIT算法基礎上進行改進，提出了許多改進的子空間類方法^［5］。然而，子空間類算法通常需要滿足信號源數目已知、多快拍以及高信噪比（signal to noise ratio， SNR）的條件，在實際水下測向環境中應用受限。同時，為避免角度估計模糊，要求陣列中相鄰兩個陣元間隔不大于信號半倍波長。

現代聲納工作頻率范圍較寬，工作頻率決定了陣元間隔以及陣元物理尺寸，當信號頻率過高時，較小的陣元間距使得半波長物理布陣難以實現，且會產生較大的陣元互耦。隨著海洋探索的不斷深入，對于多目標、集群目標的水下探測需求日益增加，對角度分辨率要求越來越高，高分辨率意味著較大的陣列孔徑，一般需要大量的陣元來擴大陣列的有效孔徑，大量的物理陣元會增加系統成本和復雜度。針對上述關于陣列尺寸、系統成本以及DOA估計精度之間存在的問題，稀疏陣列因其能夠克服陣元間隔的限制而得到巨大發展及廣泛應用。稀疏陣列構型方法打破了傳統均勻陣列構型規則，按照某種規則進行非均勻且稀疏放置，其陣元間隔不受半波長的限制，因而在同樣陣元條件下，稀疏陣列可獲得比傳統滿陣更大的陣列孔徑，提高空間角度分辨率和測角精度;換言之，在陣列尺寸一定時，采用稀疏陣列可以顯著減少陣元數量，從而降低系統成本。

當陣元數目有限時，陣元對空域信號的采樣將不滿足奈奎斯特采樣定理，常規DOA估計算法很難保證角度估計的性能。因此，如何提高有限元陣列或稀疏陣列的空間增益和角度分辨率成為DOA估計領域的熱點問題。針對互質陣中的DOA估計，研究人員在傳統MVDR算法的基礎上，對干擾噪聲協方差矩陣進行重構，取得了更優的角度估計性能，但在低SNR下，算法穩健性較差^［6］。He等^［7］提出了基于MUSIC算法的空間任意四元陣測向技術，但此類算法依然存在運算量和快拍數過大的問題。隨著對壓縮感知（compressive sensing， CS）理論^［8］和稀疏信號表征研究的不斷深入，在信號具有稀疏先驗的情況下，可以極大概率在欠采樣條件下恢復目標信號^［9］，學者們將稀疏重構理論應用于超分辨DOA估計領域。當目標在空間分布滿足稀疏先驗條件、測量矩陣滿足約束等容（restricted isometry property， RIP）條件時，可實現超分辨DOA估計^［10-12］。文獻［13］提出了一種單快拍自適應角度估計算法，可在單快拍情況下，得到較為理想的估計結果，但是單快拍DOA估計在低SNR條件下角度估計穩定性差。為了將稀疏重構思想應用于多快拍數據場景中，Cotter等^［14］提出基于多測量矢量（multiple measurement vector， MMV）模型的角度估計算法，由于陣列獲取的是多快拍數據，算法在低SNR的情況下能以更高概率得到高精度DOA估計，但其運算復雜度隨著快拍數的增加而增大。Malioutov等^［15］提出了基于奇異值分解（singular value decomposition， SVD）的l₁-SVD的DOA估計算法。該算法首先將矩陣進行SVD，再將其轉換為二階錐規劃問題，最后采用內點法等相關凸優化方法求解得到角度估計值。算法可解決多快拍情況下復雜度過大的問題。然而，由于SVD技術需要正確的信源個數給予支撐，在信源個數未知的情況下，該算法的性能將嚴重下降甚至失效。

本文提出了一種基于CS的超分辨DOA估計算法，利用場景稀疏性，構建基于CS的DOA估計模型，構造測量矩陣和l₁范數的優化函數，設計低復雜度優化算法對空間譜進行重構，算法可在信源個數未知和有限陣元條件下得到超分辨角度估計值。在構造優化問題約束條件時，利用了噪聲背景下的多快拍數據，算法可有效抑制噪聲;利用貝葉斯CS推導了正則化系數，算法能自適應獲得空間譜，算法穩健;利用修正牛頓法求解優化問題，算法運算效率大大提高。

1 陣列接收信號模型

假設接收陣列為M陣元的隨機線性陣列，采用直角坐標表示。假設空間中存在N個方向的遠場信號，所有傳感器均為各向同性。第m個陣元的輸出可表示為

y_m（t）=∑N－1n=0s（t－τ_m，n）+ε_m（t）（1）

式中：τ_m，n為遠場信號抵達第m個陣元相較于抵達參考點的時延，τ_m，n=R_m，n/c，c為信號傳播速度;ε_m（t）為噪聲，這里假定噪聲與信號是統計獨立的。對于窄帶情形，時延等價于相移，即s（t－τ_m，n）=s（t）e^－j2πf_c^τ_m，n，f_c為窄帶信號的載頻，則第m個陣元輸出為

y_m（t）=∑N－1n=0s（t）e^－j2πf_c^τ_m，n+ε_m（t）（2）

M個陣元輸出信號的矢量形式為

y（t）=∑N－1n=0a（θ_n）s（t）+ε（t）=As（t）+ε（t）（3）

式中：y（t）=［y₁（t），y₂（t），…，y_M（t）］^T為陣列輸出;s（t）=［s₀（t），s₁（t），…，s_N-1（t）］^T代表空間譜;ε（t）=［ε₁（t），ε₂（t），…，ε_M（t）］^T為噪聲;A=［a（θ₀），a（θ₁），…，a（θ_N－1）］為導向矩陣，a（θ_n）=［e^－j2πf_c^τ_1，n，e^－j2πf_c^τ_2，n，…，e^－j2πf_c^τ_M，n］^T代表導向矢量，表征了目標方向和各陣元位置之間的相位差異。

2 基于CS的超分辨角度估計

2.1 陣列角度估計模型

觀測角度范圍被分成H個角度單元，對應的導向矩陣變為大小為M×H的矩陣A=［a（θ₀），a（θ₁），…，a（θ_H－1）］，導向矢量為a（θ_h）=［e^－j2πf_c^τ_1，h，e^－j2πf_c^τ_2，h，…，e^－j2πf_c^τ_M，h］^T，當接收數據有K個快拍時，接收信號表示為

Y=AS+E（4）

式中：E=［ε（1），ε（2），…，ε（K）］代表大小為M×K的矩陣;Y=［y（1），y（2），…，y（K）］是大小為M×K的矩陣;S代表需要恢復的二維空間譜，第n行第k列元素為s_n（k）。通過向量化二維信號模型轉化為一維形式：

y=A-s+ε（5）

式中：A-=diag{A，A，…，A}是分塊矩陣，大小為MK×HK;y=vec（Y）;s=vec（S）;ε=vec（E），vec（·）指矩陣向量化，表示將矩陣的各列向量依次堆疊形成一個列向量。假設在多次快拍觀測中，目標角度不發生變化，即空時不耦合。因此，對空時譜在時間上做累積可作為空間譜估計s-（h）=∑_k|s_h（k）|，通過對譜估計結果s-（h）做檢測，可得到目標的角度估計值和個數。目標場景中只在少數觀測角度中有目標，即Nlt;lt;H，空間譜具有強稀疏特性，利用這一特性可將空間譜估計過程轉化為稀疏重構過程。在實際應用中，陣元數通常小于目標區域角度劃分網格數，A-是一個高維到低維的測量矩陣，從有限回波數據中恢復空間譜是一個病態過程。CS理論表明，在s為稀疏先驗條件時，如果測量矩陣A-滿足RIP特性，則可以從接收信號y中恢復未知空時譜矩陣s。滿足RIP特性，即存在限制等距常數δ∈（0，1），使條件（1－δ）s22≤A -s22≤（1+δ）s22成立，RIP特性與構成測量矩陣的基向量的相關性有關，相關系數越小，基的正交性越好。A～={a～（θ_h）}^H－1_h=0為歸一化的基向量集合，相互之間的相關系數為

R（A～）=maxp≠q0≤p，q≤H－1|lt;a～（θ_p），a～（θ_q）gt;|（6）

當空間譜矩陣滿足以下條件時，滿足RIP特性。

在滿足稀疏先驗以及RIP特性條件下，可將上述病態求解問題轉化為l₁范數的優化問題，從而得到目標角度信息。考慮噪聲影響，構建的l₁范數優化問題為

s=arg min{y-A-s22+ρs₁}（8）

式中：ρ為正則化系數;·2和·₁分別表示l₂范數和l₁范數;min（·）是最小化運算。

2.2 稀疏優化求解算法實現

利用優化求解算法，如正交匹配追蹤（orthogonal matching pursuit， OMP）算法^［16］、BFGS（Broyden，Fletcher，Gold-farb，Shanno）算法等^［17］可求解l₁范數優化問題，通常采用CVX、SEDUMI等內點法求解器，不利于工程應用^［18-20］，本文推導基于擬牛頓算法的低復雜度方法求解式（8）中的優化問題。為提高算法的噪聲穩健性和環境適應能力，首先推導了優化問題中的正則化系數ρ，假設噪聲矩陣E服從復高斯分布，均值為零，方差為σ²，ε的概率密度函數（probability density function， PDF）可表示為

因此，當已知s時，y的概率密度函數可表示為

基于貝葉斯CS原理，在空間譜具有強稀疏性的前提下，空間譜服從Laplace分布，s的概率密度函數可表示為

式中：V是Laplace函數尺度系數。在已知陣列接收矩陣y時，可利用最大后驗概率準則估計空時譜，s的最大后驗概率估計為

將式（10）和式（11）代入式（12）推導可得

通過以上的貝葉斯CS的推導，正則化系數為ρ=2σ²V，下面介紹估計σ²和V的方法。首先，利用常規恒虛警檢測進行粗檢測，超過檢測門限的區域判定為目標區域，低于檢測門限的區域判定為噪聲區域。由于假設噪聲滿足零均值的高斯分布，其方差σ²可通過對噪聲區域進行最大似然估計確定^［21］。由于s服從Laplace分布，因此V的最大似然可通過求max ln［PDF（s|V）］確定，也就等價于求max{ ln［PDF（s|V）］}，對ln［PDF（s|V）］關于V求導可得

?ln［PDF（s|V）］?σ=HKσ-∑HK-1i=0|s（i）|（14）

則V的最大似然估計為

V=HK∑HK－1i=0|s（i）|（15）

通過以上的推導，估計了式（13）中正則化系數ρ，由于在推導中考慮了目標和噪聲的分布特性，因此算法具有較強的噪聲抑制性能。

下面對式（13）的優化函數進行求解，對代價函數J（s）=y－A-s22+ρs₁關于s求共軛梯度為

ΔJ_s*（s）=H（s）s-2A-^Hy（16）

式中：H（s）矩陣是s的系數矩陣，可表示為

H（s）=2A-^HA-+ρΛ（s）（17）

式中：Λ（s）=diag［1/|s（hk）|²+τ］。傳統的牛頓法和擬牛頓法不適合處理包含非二次型的優化問題^［22］，特別是代價函數中包含了s的模，更增加了求解的復雜性。本文中用修正的牛頓迭代算法來求解該優化問題^［23］。由牛頓法可知，s的第l+1次迭代式為

s^l+1=s^l－β［H（s^l）］^－1ΔJ_s*（s^l）（18）

式中：β為迭代步長，［·］^－1表示矩陣的逆。如迭代步長設為β=1，把共軛梯度式（16）代入式（18）推導得

s^l+1=2［H（s^l）］^－1A-Hy（19）

當迭代滿足以下條件時，算法終止

s^l+1－s^l22s^l22lt;δ（20）

將二維空時譜在時間域上做累積即可得到目標角度空間譜

s-（h）=∑k|s_h（k）|（21）

對s-進行常規的恒虛警檢測能獲得目標的角度估計結果，其位置和個數分別表示目標的角度估計值和目標個數。

2.3 快速算法及運算復雜度分析

以上優化求解算法計算量主要集中于Hessian矩陣H（s^l）的求逆，由上面的推導可知，H（s^l）是大小為HK×HK的矩陣，用常用的Cholesky分解，每次迭代中均需要運行（HK）³/3+2（HK）²次乘法運算，算法運算量過大。

為解決Hessian矩陣求逆所引起的運算量大的問題，本文算法在第l+1次迭代運算中求解s^l+1時，采用共軛梯度法（conjugate gradient algorithm， CGA）求解。

H（s^l）s^l+1=2A-^Hy（22）

Hessian矩陣在每次迭代中均需要進行更新H（s^l）=2A-^HA-+ρΛ（s^l），在第l+1次迭代中，CGA需要完成下列方程的多次重復計算：

H（s^l）s^=2A-^HA-s^+ρΛ（s^l）s^（23）

式中：s^為迭代更新值。利用分塊對角矩陣的性質，式（23）第1項可表示為

2A-^HA-s^=2diag{A^H …A^H}diag{A …A}s^=

2diag{A^HA …A^HA}s^=2s^（24）

式（23）第2項中Λ（s^l）可表示為對角矩陣Λ（s^l）=diag［1/|s（hk）|²+τ］，因此Λ（s^l）s^是對角線上的HK個元素組成的向量與向量s^的Hadamard乘積，通過HK次乘法即能獲得矩陣相乘結果。

由于優化算法中主要運算量為乘法運算，利用所提出的快速求解算法，算法運算復雜度為O（HK），相比于直接矩陣運算，運算復雜度降低了兩個數量級。

BFGS和OMP也可以利用上述的快速矩陣乘法來提高運算效率。對于BFGS算法來說，算法主要運算量為每次迭代中的內積運算以及ΔJ_s*（s^l）的更新，由以上推導可知，ΔJ_s*（s）=H（s）s-2A-^Hy，H（s）s可利用上述的快速矩陣運算提高運算效率，BFGS算法的運算量為O（HK²）。OMP算法的主要運算量集中于最大相關運算和最小二乘估計，在每次迭代中，最大相關法運算量為O（HK），在第l次迭代運算中，最小二乘法運算量為O（HKl），因此OMP的運算量為O（HK）。

3 實驗仿真與結果分析

仿真實驗中聲速為1 500 m/s，信號載頻為1 kHz，半波長為0.75 m。假定陣列為長度為24 m的隨機布放直線陣列，陣元個數M=8。各陣元接收數據中加入均值為0的高斯白噪聲，SNR為0～10 dB。

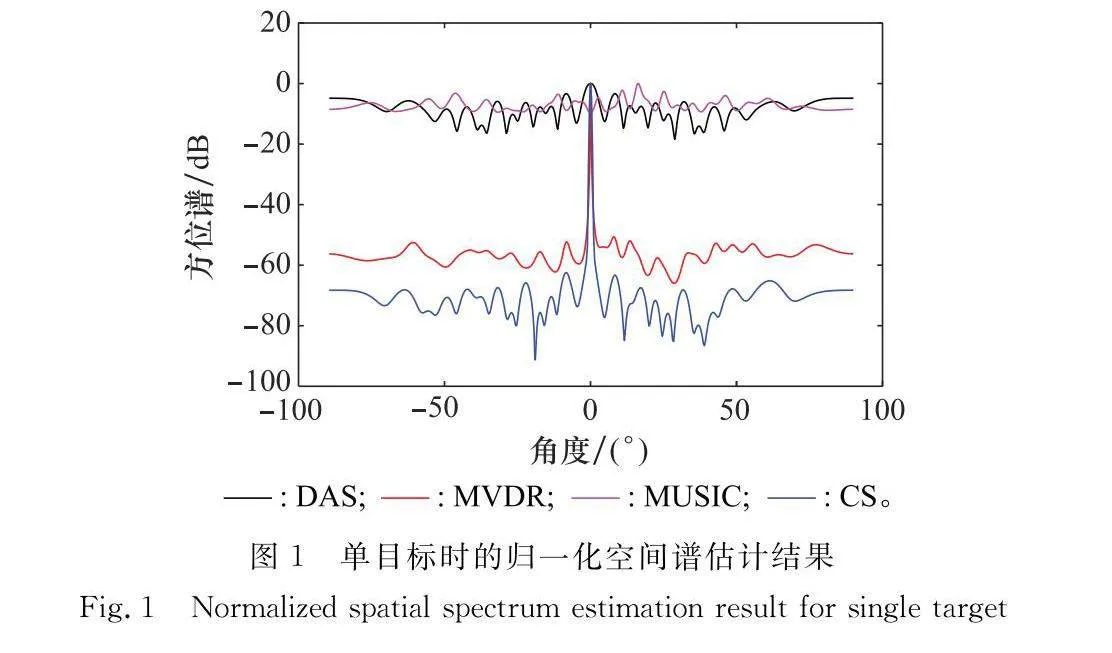
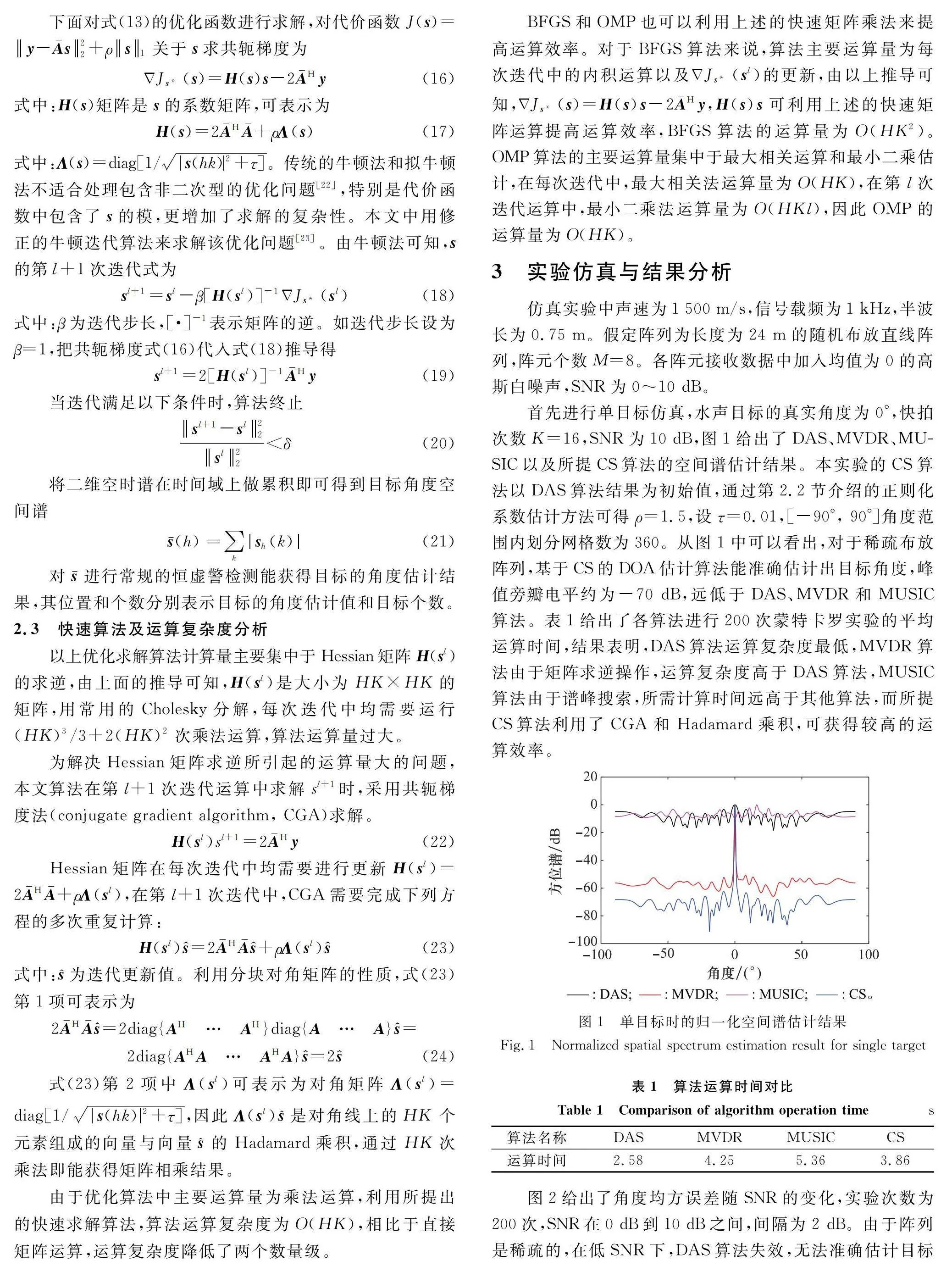
首先進行單目標仿真，水聲目標的真實角度為0°，快拍次數K=16，SNR為10 dB，圖1給出了DAS、MVDR、MUSIC以及所提CS算法的空間譜估計結果。本實驗的CS算法以DAS算法結果為初始值，通過第2.2節介紹的正則化系數估計方法可得ρ=1.5，設τ=0.01，［-90°， 90°］角度范圍內劃分網格數為360。從圖1中可以看出，對于稀疏布放陣列，基于CS的DOA估計算法能準確估計出目標角度，峰值旁瓣電平約為-70 dB，遠低于DAS、MVDR和MUSIC算法。表1給出了各算法進行200次蒙特卡羅實驗的平均運算時間，結果表明，DAS算法運算復雜度最低，MVDR算法由于矩陣求逆操作，運算復雜度高于DAS算法，MUSIC算法由于譜峰搜索，所需計算時間遠高于其他算法，而所提CS算法利用了CGA和Hadamard乘積，可獲得較高的運算效率。

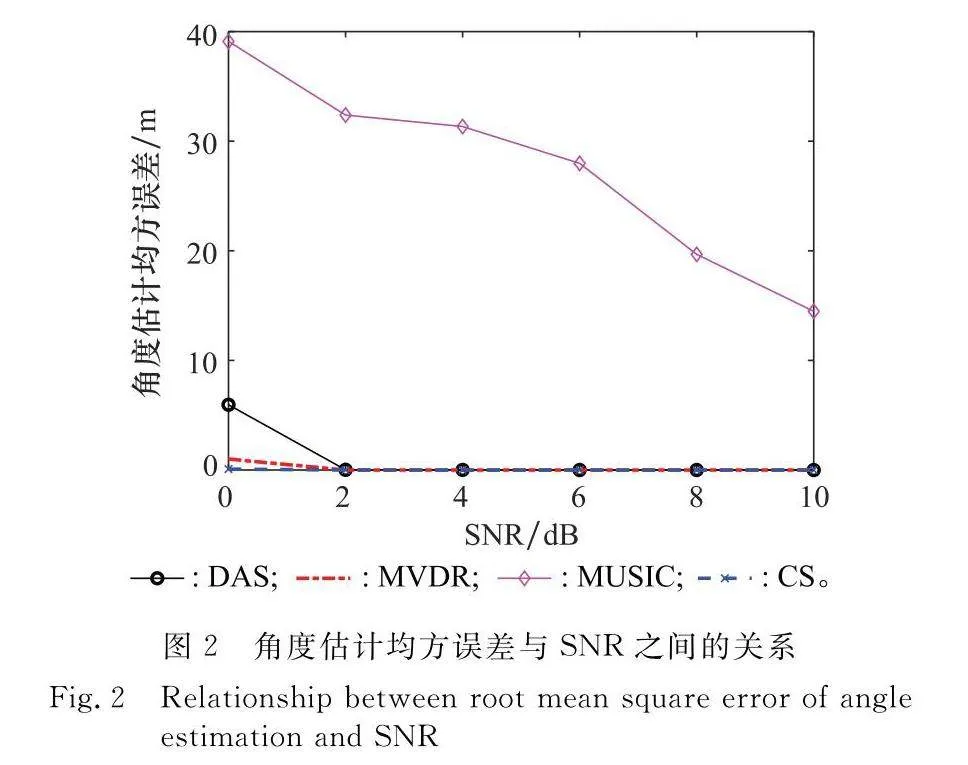
圖2給出了角度均方誤差隨SNR的變化，實驗次數為200次，SNR在0 dB到10 dB之間，間隔為2 dB。由于陣列是稀疏的，在低SNR下，DAS算法失效，無法準確估計目標角度。MUSIC算法由于快拍數較少以及目標數量未知，無法獲得有效的目標角度，MVDR算法和所提CS算法的角度估計均方誤差較低，在低SNR下依然能獲得高精度角度估計結果。

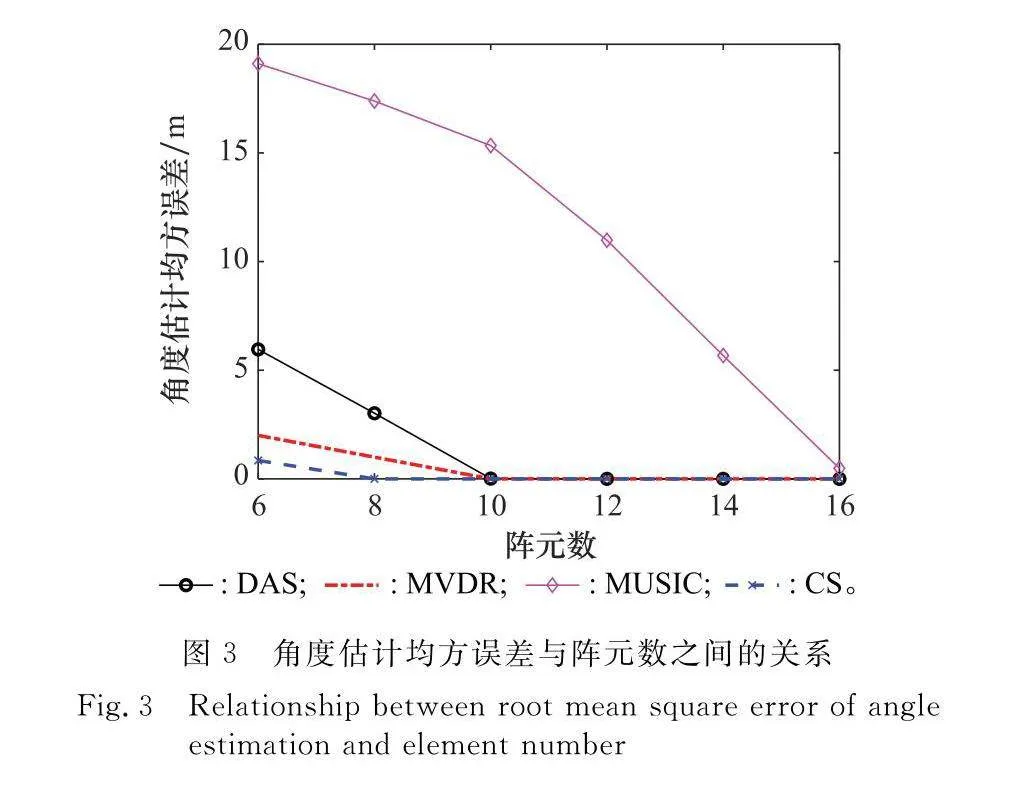
接下來，為驗證算法的稀疏恢復性能，在不同陣元數下對各算法進行實驗分析。圖3給出了角度估計均方誤差與陣元數之間的關系，選取陣元數6到16進行實驗，陣元隨機布放，SNR為10 dB，快拍數為16。從結果可以看出，在陣元數大于10時，DAS、MVDR以及CS算法角度估計均方誤差小，MUSIC在低快拍條件下欠穩健，而本文所提CS算法在陣元數為6時仍能以較高精度獲得目標角度。結果表明，所提算法在保證高精度角度估計的前提下可降低陣元數量。

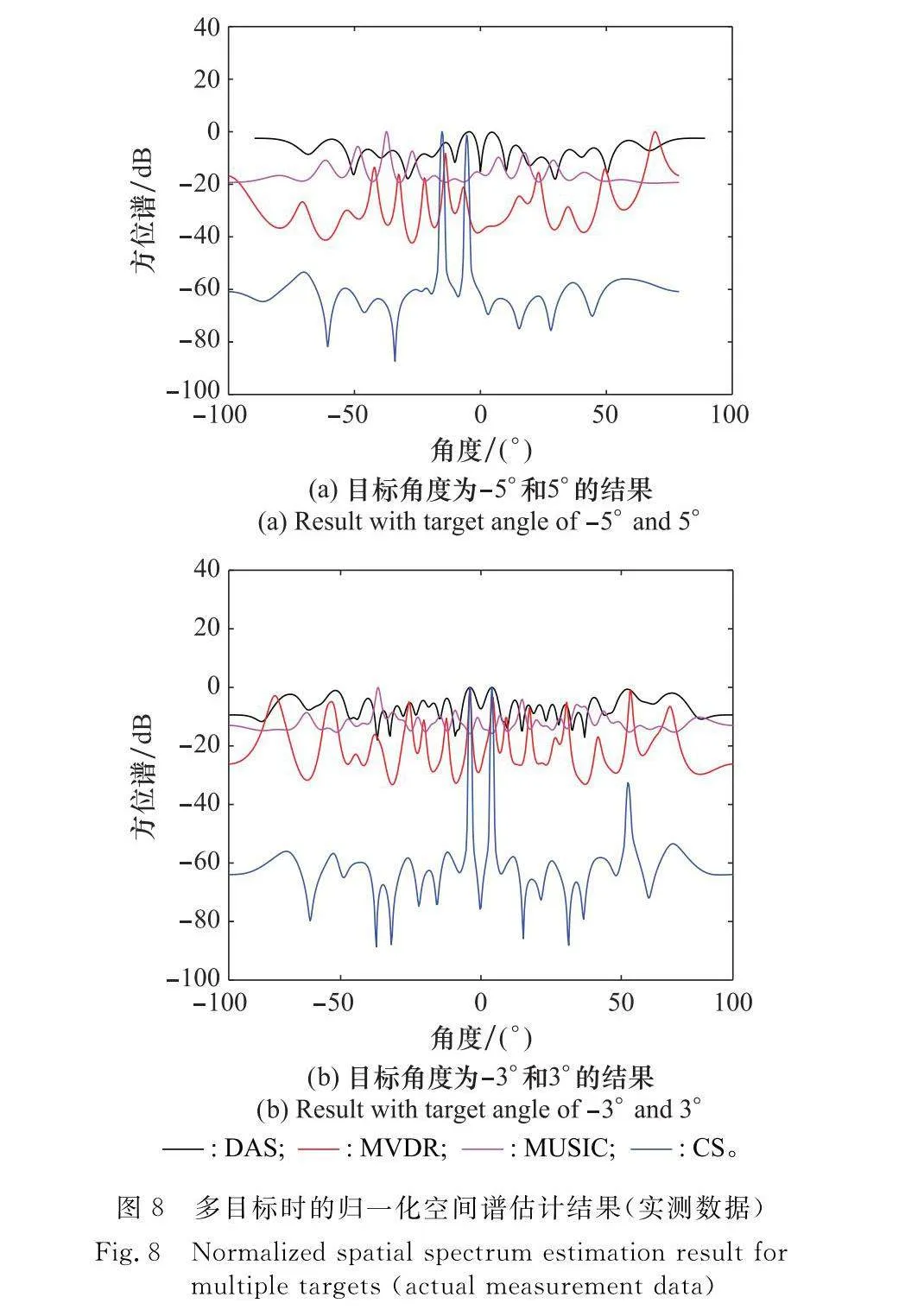
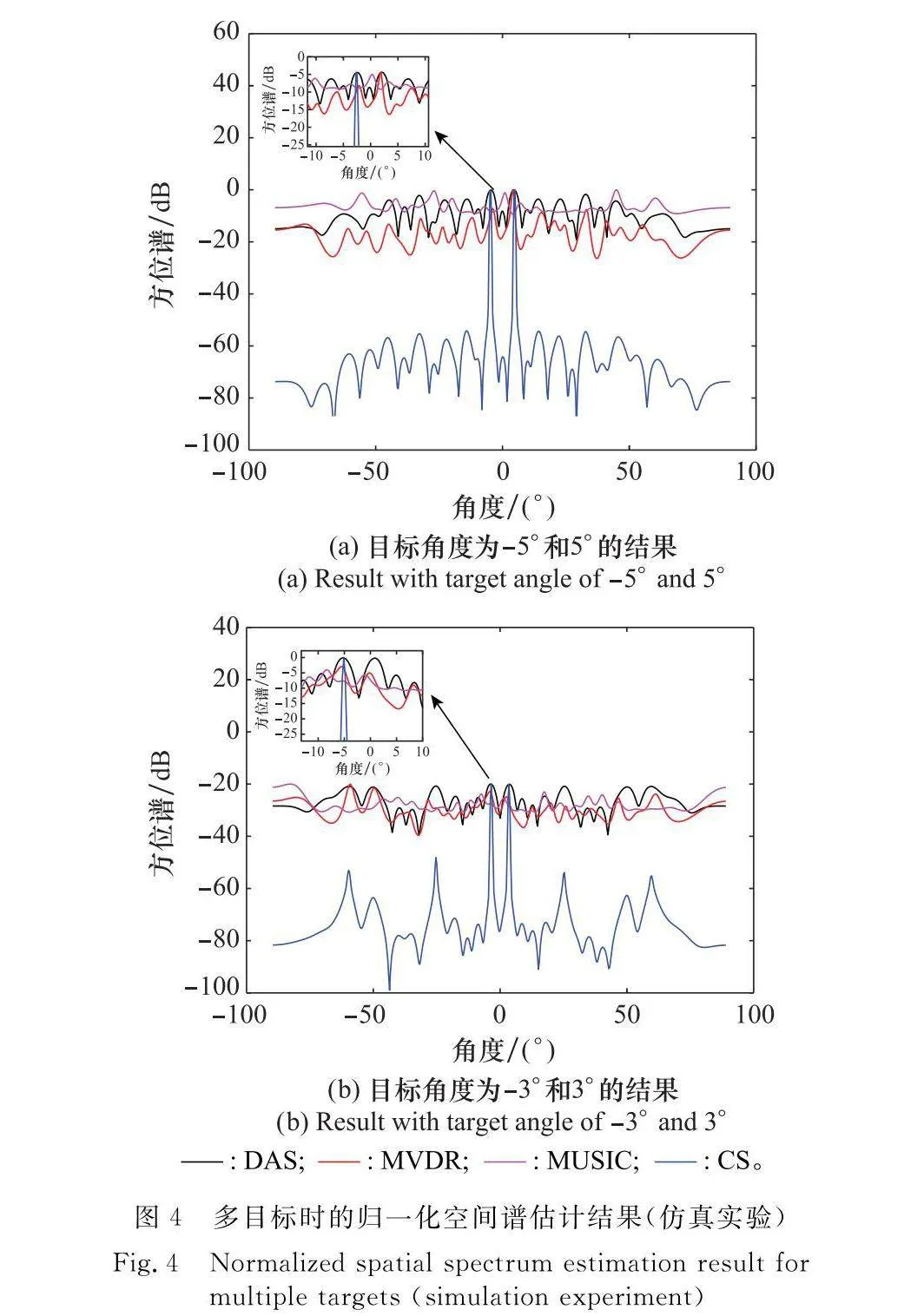
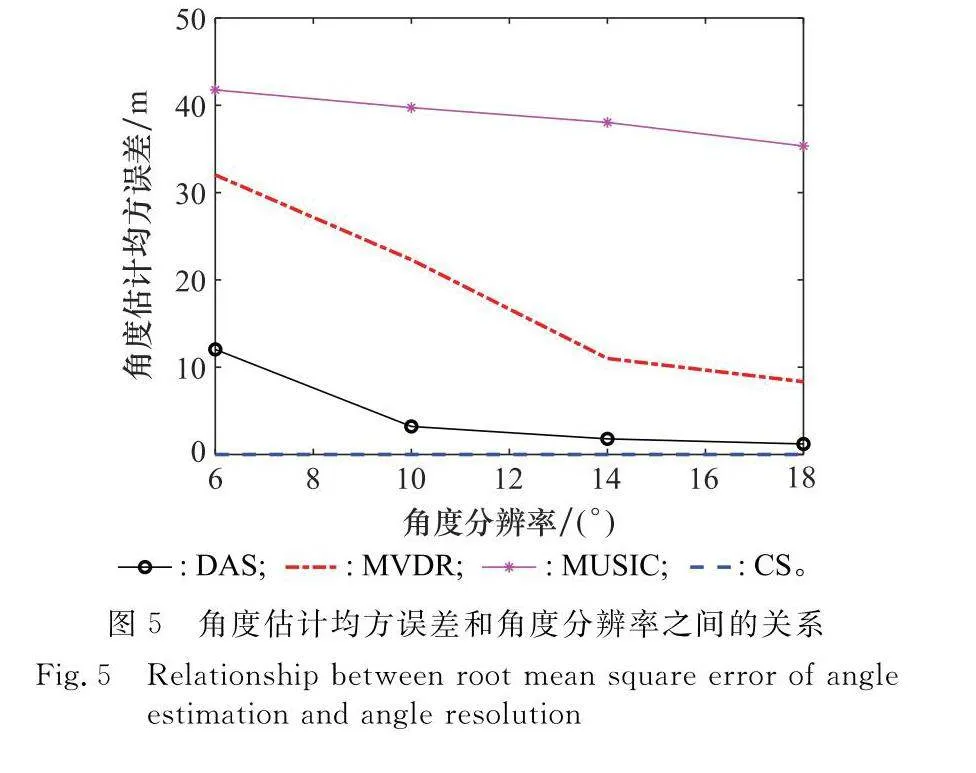
最后，通過多目標角度估計驗證算法的超分辨性能，圖4（a）中的兩個目標角度分別為-5°和5°，圖4（b）中兩個目標角度分別為-3°和3°。從圖4（a）中的結果可以看出，CS算法估計結果主瓣最尖銳，角度分辨率最高，MUSIC由于目標數量未知以及快拍數較少，無法準確恢復目標角度，雖然DAS算法和MVDR算法可恢復出兩個目標，但是由于旁瓣較高，在兩個目標間產生了一個虛假目標，當兩個目標進一步靠近，角度為-3°和3°時，DAS和MVDR算法均已無法分辨兩個目標，而本文所提算法依然能獲得良好的角度估計結果。結果表明，對于多目標應用場景，所提算法可實現臨近目標的超分辨估計。圖5給出了角度估計的均方誤差隨兩個角度間隔（角度分辨率）的變化曲線，實驗次數為200次，角度分辨率在6°到18°之間，間隔為4°。隨著角度間隔的降低，算法的估計精度越來越低，所提CS算法利用稀疏優化重構，在兩個目標相鄰較近時，依然能獲得高精度角度估計結果，算法超分辨效果顯著。

4 實驗數據處理分析

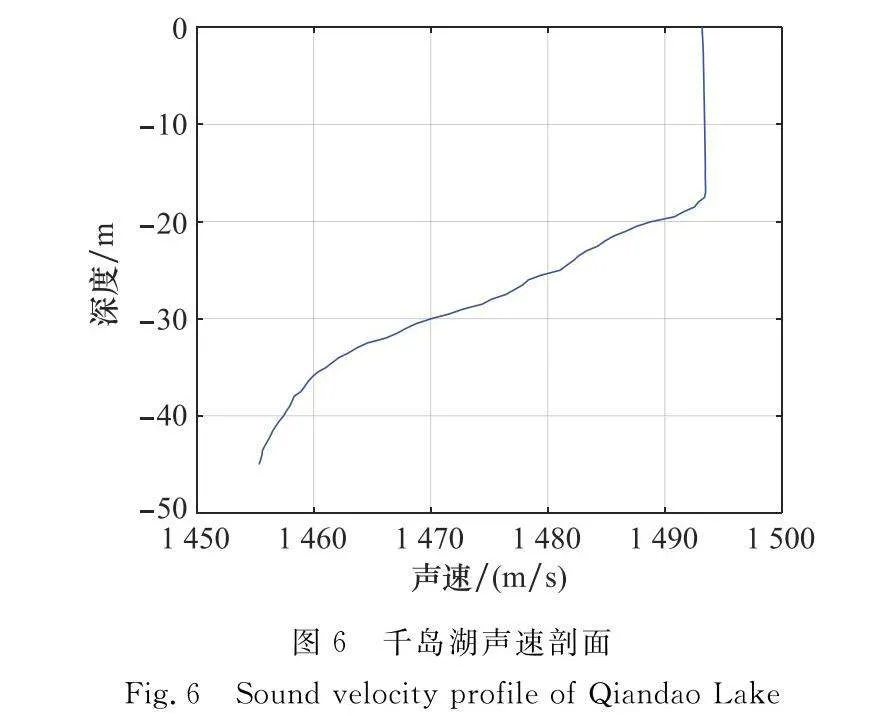
為驗證提出的基于CS的超分辨角度估計算法的性能，采用千島湖的某次湖試的數據進行處理和分析。聲速剖面如圖6所示，實驗場景中分別有單個和兩個實測目標，采用的換能器組組成了一個6元均勻直線陣列，陣列水平排布，陣元間隔為0.2 m。試驗當天水面浪高小于0.3 m且陣風，無過往船只，SNR約為-8 dB。系統發射信號為連續波，利用16個快拍數據對目標進行角度估計。正則化系數估計值為ρ=2.3。

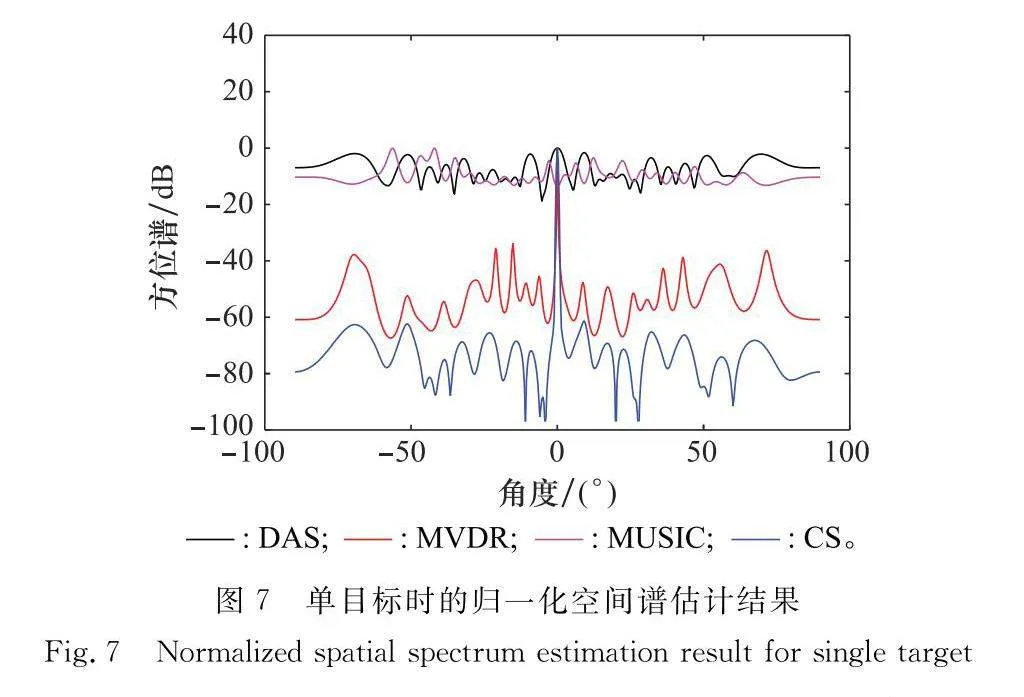
圖7給出的是實驗數據的角度估計的結果。由圖7可知，當場景中只有單個目標時，采用傳統的DAS估計技術時分辨率低，水下強噪聲使算法很難產生足夠明顯的峰值，從而嚴重影響了MUSIC算法的角度估計結果。相比于MUSIC算法，MVDR算法可得到高峰值空間譜，峰值旁瓣電平約為-50 dB，通過利用稀疏重構方法，基于CS的算法即使在強噪聲水下環境中，依然能獲得目標的高峰值空間譜，峰值旁瓣電平約為-70 dB。

圖8（a）給出了角度為-5°和5°的多目標角度估計結果，圖8（b）給出了角度為-3°和3°的多目標角度估計結果，通過多目標角度估計結果驗證算法的超分辨性能。當兩個目標角度為-5°和5°時，MUSIC算法無法確定目標點位置峰值，DAS算法和MVDR算法雖然在目標位置有峰值，但是在其他角度也同樣產生了高峰值空間譜，這會造成后續檢測中出現虛警。本文所提算法可獲得兩個目標角度的高分辨估計結果，峰值旁瓣電平約為-60 dB。當兩個目標角度繼續靠近，角度為-3°和3°時，圖6（b）中DAS、MVDR以及MUSIC算法在非目標位置產生了高峰值空間譜，大量的虛假峰值造成檢測算法無法獲得正確的目標角度信息，所提CS算法依然可以分辨出兩個目標，峰值旁瓣電平約為-50 dB。

5 結束語

本文提出了基于CS的超分辨DOA估計算法，能有效提高目標角度估計精度，具有復雜度低、分辨率高、魯棒性強的優點。該算法利用目標空間域稀疏先驗將目標角度估計問題建模為優化問題，并通過貝葉斯CS理論推導了正則化系數，保證了算法的噪聲抑制性能，設計了高效的迭代算法，運算復雜度低。算法可利用較少陣元數和較少快拍實現高精度的目標角度估計。該算法性能優于傳統算法，特別是在低SNR、有限陣元以及較少快拍條件下優于MVDR算法和MUSIC算法，有更尖銳的空間譜峰值。仿真和實測實驗驗證了該算法的有效性。未來將會根據水下探測的實際需求，將算法推廣到多種陣型，并且聯合距離維信息，實現對多目標、群目標的高精度位置估計。

參考文獻

［1］陳世進， 閆晟， 郝程鵬， 等. 一種適用于多輸入多輸出聲吶的穩健空時自適應檢測方法［J］. 聲學學報， 2022， 47（6）： 777-788.

CHEN S J， YAN S， HAO C P， et al. A robust space-time adaptive detection method for multiple-input multiple-output sonar［J］. Chinese Journal of Acoustics， 2022， 47（6）： 777-788.

［2］CAPON J. High-resolution frequency-wavenumber spectrum analysis［J］. Proceedings of the IEEE，1969， 57（8）： 1408-1418.

［3］SCHMIDT R. Multiple emitter location and signal parameter estimation［J］. IEEE Trans.on Antennas and Propagation， 1986， 34（3）： 276-280.

［4］VANDERVEEN M C， VEEN A J， PAULRAJ A. Estimation of multipath parameters in wireless communications［J］. IEEE Trans.on Signal Processing， 1998， 46（3）： 682-690.

［5］RAO B D， HARI K V S. Performance analysis of root-MUSIC［J］. IEEE Trans.on Acoustics Speech and Signal Processing， 1989， 37（12）： 1939-1949.

［6］ZHOU C， SHI Z， GU Y. Coprime array adaptive beamforming with enhanced degrees of freedom capability［C］∥Proc.of the IEEE Radar Conference， 2017.

［7］HE K， XIANG J， HAN P， et al. Performance analysis of MUSIC for arbitary array［J］. Computer Measurement and Control， 2010， 18（3）： 688-690.

［8］DONOHO D. Compressed sensing［J］. IEEE Trans.on Information Theory， 2006， 52（4）： 5406-5425.

［9］CANDES E， ROMBERG J， TAO T. Stable signal recovery from incomplete and inaccurate measurements［J］. Communications on Pure and Applied Mathematics， 2006， 59（8）： 1207-1223.

［10］ZHENG Z， YANG T C， GERSTOFT P. Joint towed array shape and directions of arrival estimation using sparse Bayesian learning during maneuvering［J］. The Journal of the Acoustical Society of America， 2020， 147（3）： 1738-1751.

［11］PING G， FERNANDEZ-GRANDE E， GERSTOFT P. Three-dimensional source localization using sparse Bayesian learning on a spherical microphone array［J］. The Journal of the Acoustical Society of America， 2020， 147（6）： 3895-3904.

［12］虞飛， 余赟， 周利輝， 等. 一種不依賴超參數的稀疏信號單快拍DOA估計方法［J］. 系統工程與電子技術， 2021， 43（4）： 894-900.

YU F， YU Y， ZHOU L H， et al. Hyperparameter-free sparse signal direction-of-arrival estimation method with single-snapshot［J］. Systems Engineering and Electronics， 2021， 43（4）： 894-900.

［13］李洪濤， 賀亞鵬， 顧陳， 等， 基于壓縮感知的單快拍自適應波束形成算法［J］. 南京理工大學學報， 2012， 36（1）： 91-95.

LI H T， HE Y P， GU C， et al. Compressive sensing based single-snapshot adaptive beamforming algorithm［J］. Journal of Nanjing University of Science and Technology， 2012， 36（1）： 91-95.

［14］COTTER S F， RAO B D， ENGAN K， et al. Sparse solutions to linear inverse problems with multiple measurement vectors［J］. IEEE Trans.on Signal Processing， 2005， 53（7）： 2477-2488.

［15］MALIOUTOV D， ?ETIN M， WILLSKY A S. A sparse signal reconstruction perspective for source localization with sensor arrays［J］. IEEE Trans.on Signal Processing， 2005， 53（8）： 3010-3022.

［16］TROPP J A， GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit［J］. IEEE Trans.on Information Theory， 2007， 53（12）： 4655-4666.

［17］NOCEDAL J， WRIGHT S J. Numerical optimization［M］. 2nd ed. Springer： New York， 2000.

［18］陳力恒， 馬曉川， 李璇， 等， 結合壓縮感知模型的稀疏陣列波束形成方法［J］. 信號處理， 2020， 36（4）： 475-485.

CHEN L H， MA X C， LI X， et al. Sparse array beamforming method combined with compressed sensing model［J］. Journal of Signal Processing， 2020， 36（4）： 475-485.

［19］MALLAT S， ZHANG Z. Matching pursuits with time frequency dictionaries［J］. IEEE Trans.on Signal Processing， 1993， 41（12）： 3397-3415.

［20］任明健， 胡國平， 周豪， 等. 基于耦合張量分解的稀疏陣列二維DOA估計算法［J］. 系統工程與電子技術， 2023， 45（4）： 958-964.

REN M J， HU G P， ZHOU H， et al. DOA estimation algorithm with two-dimensional sparse array based on coupling tensor decomposition［J］. Systems Engineering and Electronics， 2023， 45（4）： 958-964.

［21］JI S H， XUE Y， CARIN L. Bayesian compressive sensing［J］. IEEE Trans.on Signal Processing， 2008， 56（6）： 2346-2356.

［22］ZHOU H， ALEXANDER D， LANGE K. A quasi-Newton acceleration for high-dimensional optimization algorithms［J］. Statistics and Computing， 2011， 21（2）： 261-273.

［23］WU M， ZHANG L， XIA X G， et al. Phase adjustment for polarimetric ISAR with compressive sensing［J］. IEEE Trans.on Aerospace and Electronic Systems， 2016， 52（4）： 1592-1606.

作者簡介

吳 敏（1988—），女，副研究員，博士，主要研究方向為水聲信號處理、目標探測與成像、新體制聲納信號處理。

黎子浩（1996—），男，博士研究生，主要研究方向為水聲信號處理。

郝程鵬（1975—），男，研究員，博士，主要研究方向為水聲信號處理、陣列信號處理、信號檢測。

胡 橋（1977—），男，研究員，教授，博士研究生導師，博士，主要研究方向為水陸兩棲仿生機器人、水下機器人集群信號處理。