基于特征值的動態數字信道化子帶檢測算法

摘 要：

動態數字信道化接收結構通過檢測所有子帶，判斷信號是否存在，為綜合濾波器組處理提供依據，因此子帶檢測在接收結構中起著關鍵作用。針對傳統檢測算法存在低信噪比（signal-to-noise ratio， SNR）下檢測性能不高的問題，依據隨機矩陣理論，提出了基于最大最小特征值之差與平均特征值之比的檢測算法，利用平均特征值和最小特征值的極限分布規律來推導算法的檢測門限。其次，根據所有子帶數據獲取的特征值信息對所提算法進行了優化。最后，在動態數字信道化接收結構中，分析不同因素下算法的性能，表明了所提算法能夠克服低SNR的影響，子帶檢測的性能更好。

關鍵詞：

動態數字信道化接收; 子帶信號檢測; 隨機矩陣; 特征值檢測

中圖分類號：

TN 911

文獻標志碼： A""" DOI：10.12305/j.issn.1001-506X.2024.05.33

Dynamic digital channelized sub-band detection algorithm

based on eigenvalue distribution

LI Xiaohui， WAN Hongjie*， SHI Mingli， WANG Xianwen

（School of Telecommunications Engineering，Xidian University， Xi’an 710071， China）

Abstract：

The dynamic digital channelized receiving structure detects all sub-bands to determine if there is a signal. The detection results provide a basis for processing the integrated filter bank， so it plays a vital role in the receiving structure. Since the poor performance of the traditional detection algorithm under low signal-to-noise ratio（SNR），a novel detection algorithm based on the ratio of the difference between the maximum and minimum eigen values to the average eigenvalue is proposed according to the random matrix theory. The detection threshold of the algorithm is derived by using the limit distribution law of the average eigenvalue and the minimum eigenvalue. Then， the algorithm is optimized according to the eigenvalue information obtained from all sub-band data. Finally， the performance of the proposed algorithm under different factors is analyzed in the dynamic digital channelized receiving structure， which shows that the algorithm can overcome the effects of the low SNR and perform better in the sub-band detection process.

Keywords：

dynamic digital channelized receive; sub-band signal detection; random matrix; eigenvalue detection

0 引 言

隨著計算機技術的高速發展，現代戰爭向信息化、電子化發展［1］。不同陣營通過電子對抗對敵方電磁信號實施偵察、接收及分析來獲取各種信息［2］。很多電子設備被應用于電子戰，使得電磁環境也越來越復雜［3］，由于不了解敵方的通信機制，且敵方會使用保護措施來增強自身信息抗截獲的能力，所以偵收系統的處理極為麻煩［4］。為了滿足復雜的應用需求，偵收系統要具有較大的頻帶范圍、較寬的瞬時監測頻帶寬度、高靈敏度等，從而全概率接收多個有用信號且能同步檢測。而采用數字信道化技術實現的動態數字信道化接收系統則能夠很好地滿足上述需求［5］。

動態數字信道化接收結構先對接收頻帶劃分，使得在多個較窄子帶上實現寬帶信號的處理。通過檢測所有子帶的輸出，判斷是否存在信號。最后，對存在信號的子帶綜合濾波，從而實現寬帶信號中子信號的分離與提取。所以，子帶檢測結果為綜合濾波器處理提供了依據，信號的正確檢測決定了后續處理能夠準確的重構出子信號，在接收結構中起著關鍵作用。

根據檢測所需先驗信息的差異，常用的檢測方法可分為傳統檢測、半盲檢測和盲檢測［6］。傳統檢測包括匹配濾波［7］、循環平穩特征檢測［8］等，檢測前要了解信號、噪聲的功率等先驗信息。半盲檢測如能量檢測［9］，僅需了解噪聲的功率信息，且噪聲會影響檢測性能。以上兩種檢測算法雖然在特定條件下有著各自的優點，但當信噪比（signal-to-noise ratio， SNR）處于小于-20 dB的環境時，檢測性能就會很差，有一定的局限性［10］。

隨著隨機矩陣理論研究的深入，人們將其運用到檢測中［11-12］，發現在低SNR環境中也有一定的檢測效果，繼而出現了基于采樣矩陣協方差及特征值的盲檢測算法，且不用預先了解信號及噪聲的任何信息。

文獻［13-14］提出特征值最大與最小值之比（maximum-minimum eigenvalue， MME）的檢測算法，根據最大特征值滿足Tracy-Widom分布特性來構建檢驗統計量，仿真表明具有較強相關性的信號在檢測時的性能明顯高于能量檢測算法。基于MME算法，文獻［15］將平均能量與最小特征值的比值（energy with minimum eigenvalue， EME）作為統計量，分析了算法的檢測效果。文獻［16-17］提出特征值最大與最小值之差（difference between the maximum eigenvalue and the minimum eigenvalue， DMM）的檢測算法，其檢測門限和噪聲方差有關，噪聲會影響算法的性能。文獻［18］對DMM算法優化，利用矩陣的拆分重組處理，使得特征值估計更精確。文獻［19］結合采樣協方差矩陣的平均特征值（average eigenvalue， AE），提出平均與最大特征值之比（average-maximum eigenvalue， AME）的檢測算法來對頻帶檢測。文獻［6］通過當前子帶最大特征值與所有子帶最小AE之比（maximum-minimum AE， MMAE）來構建檢測算法，改進了AE的取值，提高了一定的檢測性能。文獻［20］根據噪聲條件下的特征值分布規律，提出了基于特征值直線擬合度的算法，能在較低SNR下對多帶信號完成較好的檢測效果。文獻［21］提出基于最大特征值與最小幾何AE之比的算法，從AE的幾何角度出發，提高MMAE算法的檢測效果。文獻［22］面對不能一直準確了解實際噪聲功率的問題，設計出最大特征值與矩陣跡之比的檢測算法，仿真表明可以獲得30%或更高的性能提升。文獻［23］用采樣矩陣平均特征值來衡量所有子帶平均特征值中包含信號的個數，克服了固定門限的不足，并很好地適應噪聲及信號波動帶來的影響。文獻［24］選擇最大、次大及最小特征值形成三維特征向量，然后將采樣數據分為有用類和不可用類，驗證表明能夠一定程度地提高檢測性能。

已有算法大多利用最大、最小及AE中的部分信息來構建檢驗統計量，并根據最大特征值來確定門限。一方面，這些方法未使用其余特征值，忽視了采樣協方差矩陣中所有特征值間的內在聯系，一定程度上浪費了采樣數據中的信息。另一方面，特征值之差一類算法的檢測門限和噪聲相關，使得檢測性能受到噪聲影響。

因為對采樣數據的充分使用可以提取到更多數據的特性，因此本文結合較多的特征值信息，提出基于DMME與AE之比的子帶頻譜檢測的新方法，推導出算法的檢驗統計量及判決閾值，其次根據所有子帶信號的特征值信息對所提算法加以優化，使得所提算法在低SNR情況下能夠具有較好的檢測效果。

1 子帶信號檢測理論

1.1 子帶信號的產生原理及檢測模型

數字信道化接收系統將接收到的寬帶輸入信號分析濾波處理后，輸出多個窄帶寬的信號，也稱為子帶信號，如圖1所示。

分析濾波器組將接收頻帶劃分為K個子帶，每個子帶帶寬B為2π/K，輸入x（n），通過分析濾波處理后輸出等帶寬的子帶信號是xi（m），i=0，1，…，K－1。

均勻分析濾波器組是原型低通濾波器h（t）復調制產生，通過分析濾波，第i個子帶信號為

xi（n）=x（n）hi（n）（1）

式中：表示卷積;hi（n）是第i個子帶濾波器。

根據文獻［25］，通過對均勻調制濾波器組處理前后的單載波信號進行分析，兩者的表達式非常相似，對信號的濾波處理可以看作是碼元成形函數的變化，濾波后的信號仍然保留了原信號x（t）的調制信息。因此，可以通過檢測濾波后的信號來確定子帶的輸出是否包含部分原信號。

對子帶采樣并考慮噪聲影響，可做出假設：

xi（n）=si（n）+ωi（n）， H1

ωi（n）， H0（2）

式中：si（n）是第i個子帶中的信號分量;ωi（n）是高斯噪聲分量。

假設根據某一算法得到檢驗統計量為α［xi（n）］，檢測門限為γ，對應的判決規則為

α［xi（n）］gt;γ， H1

α［xi（n）］≤γ， H0

依照判決規則，假設H1下，認為存在信號，將此時檢測到信號的正確概率記為檢測概率Pd;假設H0下，認為只有噪聲存在，將此時檢測到信號的錯誤概率記為虛警概率Pf，即：

Pd=P{α［xi（n）］gt;γ|H1}

Pf=P{α［xi（n）］gt;γ|H0}（3）

在實際的檢測算法中，通常用檢測概率Pd及虛警概率Pf評價檢測算法所能達到的性能，若要具有較好的檢測性能，需盡量使檢測概率Pd高并使虛警概率Pf低。

1.2 單通道子帶信號的多通道轉換

在動態數字信道化接收結構中，采樣數據經過分析濾波后的子帶數據一般為長度為L的單通道形式的數據向量。分析采樣數據的協方差矩陣時，需要將單通道的數據向量先轉換為多通道的數據矩陣，即將1×L的采樣數據轉換為M×N的數據矩陣形式。單通道數據向多通道轉換可以通過延時擴展、經驗模態分解及間隔采樣等方法來實現。

延時擴展法是通過延時處理將原采樣數據分為多段數據，再將多段數據合并成一個數據矩陣。設接收采樣數據為x（n），n=1，2，…，L，L是數據長度，x（n）經過延時擴展后可表示為

xi（n）=x（n+（i－1）N）（4）

式中：i表示第i個虛擬通道，且i=1，2，…，M;n=1，2，…，N，對應的M×N維數據矩陣為

X=［x（n）; x（n+N）; …; x（n+（M－1）N）］T（5）

式中：M為延時后的通道數;N為每通道的延時量。延時擴展處理簡單，但要求的采樣數較多。

經驗模態分解法是根據信號自身的局部時間特征，將信號通過多個固有模態函數和的形式來表示，可以把較為復雜的信號分解成多個帶有一定物理含義的分量［26］。通過經驗模態分解處理后的單通道采樣數據可表示為

x（t）=∑Ni=1ci（t）+rN（t）（6）

式中：x（t）為單通道的采樣數據;ci（t）為第i個分量;rN（t）為殘余量。因此多通道表示為

X=［c1（t）; c2（t）; …; cN（t）; rN（t）］T（7）

經驗模態分解法通過分量表示信號，進而表示為矩陣形式，但是不適用于所有信號的處理，并且計算的復雜度較高。

間隔采樣法是對單通道的過采樣數據進行重采樣，得到多個新數據向量，再構建多維數據矩陣。設接收到的過采樣數據為x（n），n=0，1，2，…，L－1，周期為Ts。以Ts的M倍時間對x（n）進行重采樣，新的采樣序列為

xi（n）=x（Mn+i－1）， i=1，2，…，M（8）

式中：n=1，2，…，M，表示M個新采樣序列;周期為T，且T/Ts=M。因此采樣數據矩陣為

X=［x1（n），x2（n），…，xM（n）］T（9）

使用間隔采樣法時要求輸入數據是過采樣的，意味著在接收系統中對模擬數字轉換器（analog to digital converter， ADC）的采樣率要求較高。但對于數字信道化接收結構中經過分析濾波處理后的子帶來說，其帶寬遠小于輸入帶寬，得到的子帶數據均是過采樣的，可以很好地利用過采樣法進行數據維數的轉換。

1.3 基于隨機矩陣理論的子帶檢測

隨機矩陣理論能夠有效地處理大維數數據，并且一些隨機矩陣的統計特性可以和無線系統結合起來，通過隨機矩陣的統計特性來反映無線系統的特點，可以更好地理解系統性能。隨機矩陣理論中的非漸近隨機矩陣理論適用于確定維數的數據處理，將以往的研究應用到檢測領域，促進了檢測技術的發展。

假設在系統接收端采樣數據，處理后獲得一個M×N維的采樣數據矩陣X，則

2.3 算法步驟

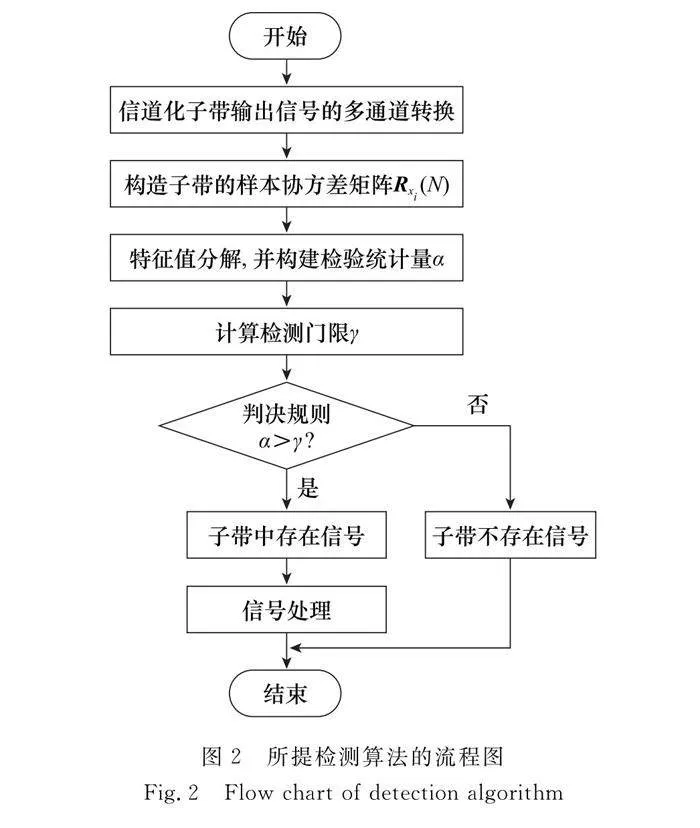
根據所提算法的推導過程，其具體步驟如下：

步驟 1

對經過動態數字信道化接收結構處理一共得到K個子帶信號。

步驟 2

對于DMME-AE算法，用間隔采樣法將第i個子帶的采樣數據轉換為M×N維的數據矩陣，并求出對應的采樣協方差矩陣Rxi（N）。對于DMME-MAE算法，需要求出所有子帶的采樣協方差矩陣Rxi（N）。

步驟 3

對于DMME-AE算法，對矩陣Rxi（N）通過特征值分解的處理，并求出特征值的最大值、最小值及當前子帶的AE。對于DMME-MAE算法，求出所有子帶采樣矩陣的AE，找出MAE。

步驟 4

根據所提算法確定檢驗統計量α。

步驟 5

依據實際的情況，確定一定大小的虛警概率Pf，得到檢測門限γ。

步驟 6

根據判決規則，對第i個子帶進行判定，如果αgt;γ時，則認為該子帶存在信號;如果αlt;γ，則認為該子帶不存在信號。

上述算法步驟對應的流程圖如圖2所示。

3 仿真實驗與結果分析

基于動態數字信道化接收結構，將所提的DMME-AE及DMME-MAE檢測算法應用其中，通過具體的仿真實驗來對算法進行仿真。首先，仿真了算法的檢測門限，通過和噪聲環境下的檢驗統計量對比，說明了門限設置的有效性。然后通過改變參數來分析影響檢測門限及算法性能的因素，如SNR、采樣數據矩陣的行數及每行的采樣點數。最后，在仿真過程中對比現有算法，實驗結果驗證了所提算法具有較好的檢測性能。

3.1 檢測門限有效性的分析

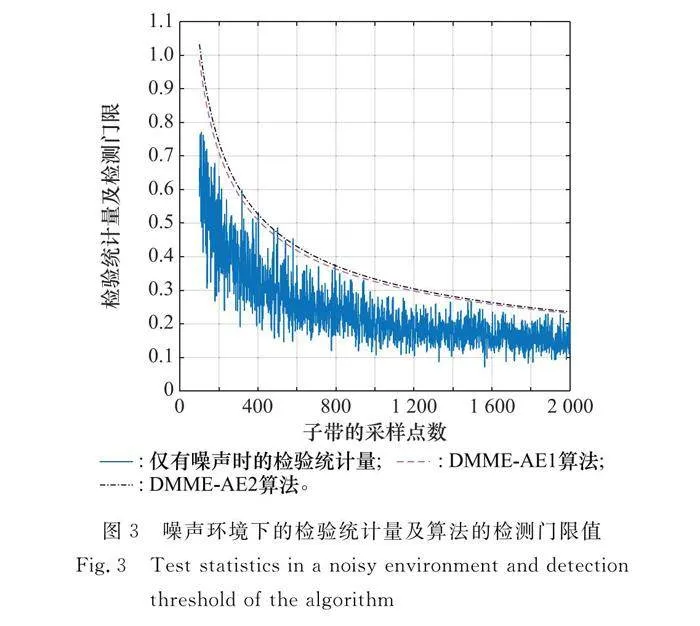
對經過分析濾波處理后的每個子帶的數據，通過間隔采樣轉換為采樣數據矩陣的形式，將采樣矩陣的行數M固定為5，選擇大小為0.01的虛警概率Pf。在只接收噪聲分量時，依次改變采樣數據矩陣每行采樣點數N的大小，探究此時算法的檢驗統計量與檢測門限關系。

由第2節、第3節的分析可知，DMME-AE算法和DMME-MAE算法有相同的檢測門限，此時僅通過DMME-AE算法的兩個檢測門限來說明。

當給定采樣矩陣行數和虛警概率，按照檢測算法的判決原則，算法的檢驗統計量是根據噪聲的信息得到，所以要小于檢測門限。如圖3所示，根據DMME-AE算法計算出的檢測門限基本都大于僅有噪聲時的檢驗統計量，其檢驗統計量的個別取值超過了檢測門限的曲線，這是由于設定了相應的虛警概率，因此存在誤判的情況。

其次，DMME-AE1與DMME-AE2算法的門限值非常接近，且通過增加采樣數據矩陣每行的采樣點數，兩者門限值之間的差距逐漸減小。另外DMME-AE1算法的檢測門限值總是低于DMME-AE2算法，使得DMME-AE1算法的檢測性能在應用中會比DMME-AE2算法好。同時DMME-AE2算法檢測門限值始終處于最大，與DMME-AE1算法相比和檢驗統計量距離更遠，對應更小的虛警概率，但當檢驗統計量較小時的檢測效果要較差，也降低了一定的檢測性能。

最后，兩種算法的檢測門限的大小和子帶的采樣點數有關，采樣點數越多，檢測門限越小，所以面對不同的檢測情況，檢測門限也能夠進行調節來適應。因此，根據仿真結果，能夠驗證所提算法的檢測門限是有效的。

3.2 算法性能的分析

在動態數字信道化接收結構中，利用仿真平臺對DMME-AE及DMME-MAE算法的檢測性能進行仿真，給定虛警概率Pf，通過衡量不同因素下算法的檢測概率Pd，來分析算法的檢測效果。并與MME、AME及MMAE等檢測算法進行比較，進而對所提算法的性能進行評估。仿真設置系統帶寬B為1 000 MHz，系統采樣頻率fs為2 000 MHz，整個接收頻帶劃分為64子帶，寬帶輸入信號可采用線性調頻脈沖及正余弦信號的組合形式。將寬帶輸入信號分析濾波處理后，應用本文所提算法來對子帶輸出檢測。

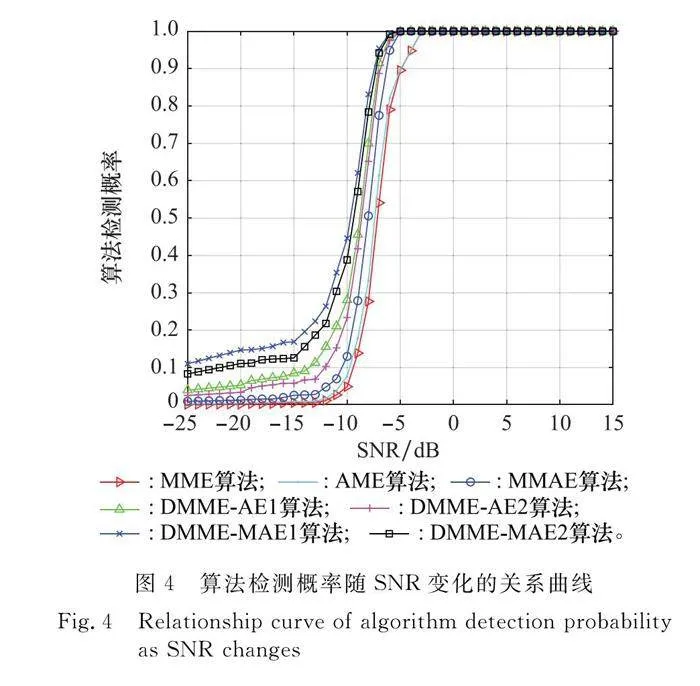
首先，探究不同SNR值對算法檢測性能的影響，SNR反映噪聲對信號的影響，進一步影響算法的檢驗統計量。設定每個子帶共采樣的數據長度L為3 000，虛警概率Pf為0.01，采樣數據進行多通道轉換后的行數M為6，每行采樣點數N為500。SNR值在-25～15 dB之間，步進1 dB，并完成10 000次的蒙特卡羅仿真實驗。

圖4的仿真結果表示算法檢測概率受SNR影響而產生變化。7種算法的檢測概率都隨著SNR的增大而提高，在-25～-15 dB之間，檢測概率緩慢增加，在-15～-5 dB之間，各算法的檢測概率都急劇增大，當大于-5 dB后趨于平緩。DMME-MAE1算法的檢測概率始終最大，在-8 dB的檢測概率為82.7%，其他算法在-8 dB時檢測概率從大到小依次是DMME-MAE2算法78.9%、DMME-AE1算法68.9%、DMME-AE2算法64%、MMAE算法49.2%、AME算法32.2%、MME算法25.6%。這說明DMME-MAE1算法的檢測效果是高于其他算法的，在-6 dB時的檢測概率已經逼近于1，而對應的MME算法的檢測概率一直最小，且性能也最差。

DMME-MAE1算法的檢測性能要優于DMME-MAE2算法，是因為在相同的檢驗統計量下，前者更低的檢測門限使得其檢測性能略好，這也是DMME-AE1算法相比DMME-AE2算法檢測性能較高的原因。同時DMME-MAE算法結合其他子帶的特征值信息選取檢驗統計量，使得其檢測性能要高于DMME-AE算法。

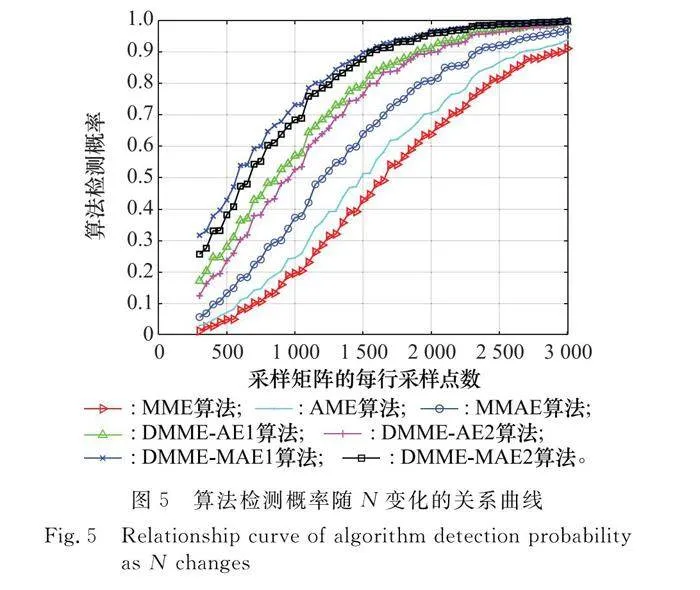
然后，對于采樣數據矩陣中每行不同的采樣點數N，來分析算法的檢測性能。根據算法檢測門限的表達式，僅與信道化后根據子帶采樣數據多通道轉換后的M×N維采樣矩陣的行數M和列數N有關，M和N的取值會直接影響算法檢測門限的大小，因此可先將行數M固定，取值為6，通過改變每行的采樣點數N來對比研究。設定SNR為-10 dB，虛警概率Pf為0.01，N在300～3000之間，變化步進為50點，并完成10 000次蒙特卡羅仿真實驗，圖5為算法檢測概率受N影響的變化。

如圖5所示，隨著子帶采樣點數的增大，7種算法的檢測概率逐步提高，即表示算法的檢測性能有所提升。DMME-MAE1算法的檢測概率始終處于最大，檢測性能顯著好于其他檢測算法，當逐漸增大采樣點數后，7種算法的性能差距逐步縮小。

在采樣點數比較小時，所提的4種算法相比已有算法能夠實現更高的檢測概率，當N增加到1 600時，DMME-MAE1算法的檢測概率已經超過90%，達到91.4%，其他算法從大到小依次是DMME-MAE2算法的89.8%、DMME-AE1算法的84%、DMME-AE2算法的81.8%、MMAE算法的68.9%、AME算法的54.9%、MME算法的46.5%。當N為2 600時，DMME-MAE1算法的檢測概率能夠達到99%，因此可以說明子帶采樣矩陣每行的采樣點數能夠提高檢測算法的檢測概率，并且所提算法能夠在采樣較少的情況下獲得更好的檢測性能。

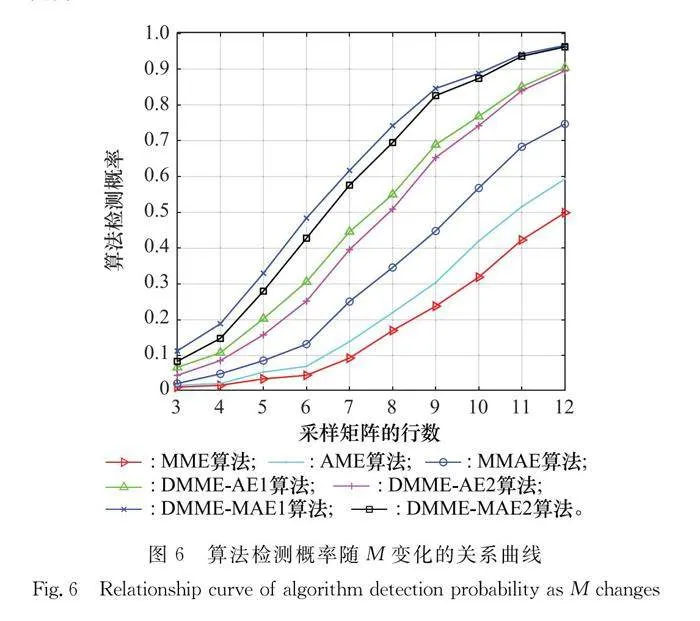
最后，研究算法檢測概率與每個子帶采樣矩陣行數M之間的關系，并分析算法的檢測性能。將采樣數據矩陣每行的點數N固定，取值為500，設定SNR為-10 dB，虛警概率Pf為0.01，M在3～12之間，步進為1。

如圖6所示，隨著子帶采樣矩陣行數的增加，所提及對比算法的檢測概率顯著增大。采樣矩陣行數的增加相當于增加了子帶的采樣點數，并且增加了采樣矩陣的特征值數量，此時AE會更加完整地包含采樣矩陣的信息，而所提算法應用了AE的分布特性，因此在相同的M值下所提算法能夠獲得更好的檢測概率，體現出更好的檢測性能。具體來說，DMME-MAE1算法的檢測概率始終處于最大，所以該算法的檢測性能最好。其次，M值較小時，所提4種算法的檢測概率提高的相對較小，但隨著M增大，檢測概率迅速增加，當M增大到10時，DMME-MAE1算法的檢測概率已經超過90%，達到91.0%，其他算法從大到小依次是DMME-MAE2算法的89.2%、DMME-AE1算法的77%、DMME-AE2算法的75%、MMAE算法的56%、AME算法的39.8%、MME算法的30.7%，因此體現出了所提算法的優勢。

通過以上仿真，對7種算法進行實驗對比，SNR、采樣矩陣每行的采樣點數及采樣矩陣的行數都會影響算法的檢測概率，并且SNR、N和M的增大會提高算法的檢測概率。同時相比MME、AME、MMAE算法，所提的DMME-MAE和DMME-AE算法能夠保持更高的檢測概率，并且在較低的SNR、N和M下也能夠優于其他3種算法，具有明顯的優勢，其中DMME-MAE1算法的檢測概率最高，檢測性能最好，體現了較強的檢測能力和可靠性。因為在任何情況下信號與噪聲的特征值差異都是存在的，所以基于特征值來構建檢驗統計量并推導檢測門限，進而區分信號與噪聲，因此所提算法具有更好的檢測性能。

4 結 論

本文通過對采樣數據的特征值分析，研究動態數字信道化接收結構中的子帶檢測算法。在分析采樣數據的協方差矩陣時，用較多的特征值信息來獲取更好的檢測性能。首先，研究矩陣特征值的分布特性，給出了基于DMME與AE之比的子帶輸出檢測算法，構造出檢驗統計量，并且利用最小特征值的極限分布規律來推導檢測門限，提高了低維度下對數據特征描述的準確性。然后，根據所有子帶信號的特征值信息對所提算法進行優化，進一步提高了檢測算法的性能。最后，在動態數字信道化接收結構中，將所提的DMME-AE及DMME-MAE子帶檢測算法應用其中，分析不同因素下算法所表現出的性能，表明了所提算法能夠克服低SNR的影響，表現出更好的子帶檢測性能。

參考文獻

［1］ WANG L， WANG K D， ZHAO R Q， et al. An efficient real-time digi-tal channelization method based on frequency-domain windowing［C］∥Proc.of the 4th International Conference on Information Communication and Signal Processing， 2021： 533-537.

［2］ GHELFI P， SCOTTI F， ONORI D， et al. Photonics for ultrawideband RF spectral analysis in electronic warfare applications［J］. IEEE Journal of Selected Topics in Quantum Electronics， 2019， 25（4）： 8900209.

［3］ 程翔， 王軒. 復雜電磁環境構建及效能評估發展與構想［J］. 雷達與對抗， 2021， 41（4）： 11-14，19.

CHENG X，WANG X. Development and conception of construction of complex electromagnetic environment and efficiency eva-luation［J］. Radar amp; ECM， 2021， 41（4）： 11-14，19.

［4］ 廖紅舒. 通信偵察信號處理關鍵技術研究［D］. 成都：電子科技大學， 2011.

LIAO H S. A study of key technologies of signal processing for communication reconnaissance［D］. Chengdu：University of Electronic Science and Technology of China， 2011.

［5］ ZHANG J J， LI J. RF channelization technology［M］. Cham： Springer International Publishing， 2022.

［6］ 胡君朋. 寬帶無線信號偵測中的動態信道化技術研究［D］. 長沙：國防科技大學， 2016.

HU J P. Research on dynamic channelization technique for broadband wireless signal reconnaissance［D］. Changsha： National University of Defense Technology， 2016.

［7］ ARJOUNE Y， MRABET Z E， GHAZI H E， et al. Spectrum sensing： enhanced energy detection technique based on noise measurement［C］∥Proc.of the IEEE 8th Annual Computing and Communication Workshop and Conference， 2018： 828-834.

［8］ SHERBIN M K， SINDHU V. Cyclostationary feature detection for spectrum sensing in cognitive radio network［C］∥Proc.of the International Conference on Intelligent Computing and Control Systems， 2019： 1250-1254.

［9］ AWIN F， ABDEL-RAHEEM E， TEPE K. Blind spectrum sensing approaches for interweaved cognitive radio system： a tutorial and short course［J］. IEEE Communications Surveys Tutorials， 2019， 21（1）： 238-259.

［10］ YUCEK T， ARSLAN H. A survey of spectrum sensing algorithms for cognitive radio applications［J］. IEEE Communications Surveys Tutorials， 2009， 11（1）： 116-130.

［11］ TAO T. Topics in radom matrix theory［M］. Rhode： American Mathematical Society， 2012.

［12］ MARCENKO V A， PASTUR L A. Distribution of eigenvalues for some sets of random matrices［J］. Mathematics of the USSR-Sbornik， 1967， 114（4）： 507-536.

［13］ ZENG Y H， LIANG Y C. Maximum-minimum eigenvalue detection for cognitive radio［C］∥Proc.of the 18th International Symposium on Personal， Indoor and Mobile Radio Communications， 2007.

［14］ CHAURASIYA R B， SHRESTHA R. Hardware-efficient and fast sensing-time maximum-minimum-eigenvalue-based spectrum sensor for cognitive radio network［J］. IEEE Trans.on Circuits and Systems I： Regular Papers， 2019， 66（11）： 4448-4461.

［15］ ZENG Y， LIANG Y C. Eigenvalue-based spectrum sensing algorithms for cognitive radio［J］. IEEE Trans.on Communications， 2009， 57（6）： 1784-1793.

［16］ 王穎喜， 盧光躍. 基于最大最小特征值之差的頻譜感知技術研究［J］. 電子與信息學報， 2010， 32（11）： 2571-2575.

WANG Y X， LU G Y. DMM based spectrum sensing method for cognitive radio systems［J］. Journal of Electronics amp; Information Technology， 2010， 32（11）： 2571-2575.

［17］ 許煒陽， 李有均， 徐宏乾， 等. 基于隨機矩陣非漸近譜理論的協作頻譜感知算法研究［J］. 電子與信息學報， 2018， 40（1）： 123-129.

XU W Y， LI Y J， XU H Q， et al. Study on cooperative spectrum sensing algorithm based on random matrix non-asymptotic spectral theory［J］. Journal of Electronics amp; Information Technology， 2018， 40（1）： 123-129.

［18］ 趙知勁， 胡偉康. 改進的最大最小特征值之差的頻譜感知算法［J］. 電子技術應用， 2014， 40（8）： 119-121，125.

ZHAO Z J， HU W K. Improved spectrum sensing algorithm based on DMM［J］. Application of Electronic Technique， 2014， 40（8）： 119-121，125.

［19］ 徐家品， 楊智. 基于隨機矩陣特征值比的頻譜感知改進算法［J］. 電波科學學報， 2015， 30（2）： 282-288.

XU J P， YANG Z. Improved spectrum sensing algorithms based on eigenvalue ratio of random matrix［J］. Chinese Journal of Radio Science， 2015， 30（2）： 282-288.

［20］ 陳亞. 基于MWC的數字接收機結構以及信號檢測方法的研究［D］.哈爾濱：哈爾濱工程大學， 2016.

CHEN Y. Digital receiver structure and the research of signal detection method based on MWC［D］. Harbin：Harbin Engineering University， 2016.

［21］ ZHANG C J， LI S S， DENG Z A， et al. An improved eigenvalue-based channelized sub-band spectrum detection method［C］∥Proc.of the Advanced Hybrid Information Processing， 2019： 244-251.

［22］ LIU C， WANG J， LIU X M， et al. Maximum eigenvalue-based goodness-of-fit detection for spectrum sensing in cognitive radio［J］. IEEE Trans.on Vehicular Technology， 2019， 68（8）： 7747-7760.

［23］ 胡君朋， 古兆兵， 齊卓礫， 等. 基于最小描述長度準則的數字信道化接收機頻譜檢測方法［J］. 測控技術， 2020， 39（9）： 15-19.

HU J P， GU Z B， QI Z L， et al. Spectrum sensing method used in digital channelized receiver based on minimum description length criterion［J］. Measurement amp; Control Technology， 2020， 39（9）： 15-19.

［24］ GIRI M K， MAJUMDER S. On eigenvalue-based cooperative spectrum sensing using feature extraction and maximum entropy fuzzy clustering［J］. Journal of Ambient Intelligence and Humanized Computing， 2023， 14（8）： 10053-10067.

［25］ 劉小蒙. 軟件無線電中動態信道化技術研究與實現［D］. 鄭州： 解放軍信息工程大學， 2016.

LIU X M. Research and implementation of dynamic channelization in software radio［D］. Zhengzhou： Information Engineering University， 2016.

［26］ 周振宇. 動態數字信道化接收機及其子帶頻譜檢測技術研究［D］. 哈爾濱：哈爾濱工程大學， 2020.

ZHOU Z Y. Research on dynamic digital channelization recei-ver and its subband spectrum detection technology［D］. Harbin： Harbin Engineering University， 2020.

［27］ RANINEN E， OLLILA E. Bias adjusted sign covariance matrix［J］. IEEE Signal Processing Letters， 2022， 29： 339-343.

［28］ TULINO A M， VERDU S. Random matrix theory and wireless communications［J］. Foundations and Trends in Communications and Information Theory， 2004， 1（1）： 3-73.

［29］ JOHNSTONE I M. On the distribution of the largest eigenva-lue in principal components analysis［J］. The Annals of Statistics， 2001， 29（2）： 295-327.

［30］ TRACY C A， WIDOM H. On orthogonal and symplectic matrix ensembles［J］. Communications in Mathematical Physics， 1996， 177（3）： 727-754.

作者簡介

李曉輝（1972—），女，教授，博士，主要研究方向為寬帶無線通信、無線資源管理。

萬宏杰（1996—），男，碩士研究生，主要研究方向為寬帶無線通信、數字信號處理。

石明利（1997—），男，博士研究生，主要研究方向為智能超表面、大規模多輸入多輸出。

王先文（1995—），男，碩士研究生，主要研究方向為物理層基帶信號處理。