例談逆向思維法在高中力學(xué)解題中的應(yīng)用

【摘要】本文首先闡述逆向思維法的優(yōu)勢(shì)，然后通過高中力學(xué)中的兩則例題詳細(xì)分析逆向思維法的應(yīng)用策略．研究表明，逆向思維法能夠幫助學(xué)生打破常規(guī)思維定式，開拓解題思路，提高解題效率和準(zhǔn)確性，培養(yǎng)其創(chuàng)新思維能力．

【關(guān)鍵詞】逆向思維法；高中力學(xué)；解題應(yīng)用

逆向思維法是一種從問題的相反方向或結(jié)果出發(fā)，通過逆向推理和分析來解決問題的思維方式．它能夠幫助學(xué)生突破傳統(tǒng)思維的束縛，發(fā)現(xiàn)問題的本質(zhì)，從而快速、準(zhǔn)確地解決問題．本文將通過具體的例子，探討逆向思維法在高中力學(xué)解題中的應(yīng)用．

1 逆向思維法的優(yōu)勢(shì)

在高中力學(xué)的學(xué)習(xí)中，力學(xué)部分一直是重點(diǎn)和難點(diǎn)．而在解決力學(xué)問題時(shí)，思維方法的選擇往往決定了學(xué)生解題的效率和準(zhǔn)確性．逆向思維法作為一種獨(dú)特的思維方式，在高中力學(xué)解題中展現(xiàn)出了顯著的優(yōu)勢(shì)．

1.1 簡(jiǎn)化問題，提高解題效率

逆向思維法是一種與常規(guī)思維方向相反的思考方式．在高中力學(xué)中，當(dāng)面對(duì)復(fù)雜的問題時(shí)，常規(guī)的正向思維可能會(huì)陷入困境，而逆向思維卻能為學(xué)生開辟一條新的解題路徑．

例如 在處理末速度為零的勻減速直線運(yùn)動(dòng)的問題時(shí)，如果按照常規(guī)的正向思維，從初始狀態(tài)逐步推導(dǎo)到最終狀態(tài)，計(jì)算過程可能會(huì)較為繁瑣．但如果采用逆向思維，將其看作初速度為零的勻加速直線運(yùn)動(dòng)的逆過程，問題就會(huì)變得簡(jiǎn)單許多．可以直接運(yùn)用勻加速直線運(yùn)動(dòng)的公式和規(guī)律來求解，大大減少了計(jì)算量和思維難度．

1.2 培養(yǎng)創(chuàng)新思維能力

逆向思維法有助于培養(yǎng)學(xué)生會(huì)的創(chuàng)新能力和應(yīng)變能力．在面對(duì)新的、陌生的力學(xué)問題時(shí)，能夠打破常規(guī)，從不同的角度思考問題，尋找解決問題的方法．這種能力不僅在高中力學(xué)學(xué)習(xí)中至關(guān)重要，對(duì)于學(xué)生今后的學(xué)習(xí)和生活也具有重要意義[1]．

1.3 增強(qiáng)對(duì)物理知識(shí)的理解和應(yīng)用

逆向思維法還能夠幫助學(xué)生更深刻地理解力學(xué)概念和規(guī)律．通過從結(jié)果反推原因，讓學(xué)生能夠清晰地看到各個(gè)物理量之間的內(nèi)在聯(lián)系，從而加深對(duì)力學(xué)知識(shí)的掌握．

例如 在分析物體碰撞后的運(yùn)動(dòng)狀態(tài)時(shí)，從最終的靜止或運(yùn)動(dòng)狀態(tài)逆向思考碰撞瞬間的能量和動(dòng)量變化，有助于理解碰撞過程中的守恒定律．在實(shí)際解題中，運(yùn)用逆向思維法需要學(xué)生具備扎實(shí)的基礎(chǔ)知識(shí)和敏銳的洞察力．要對(duì)力學(xué)的基本概念、公式和定理有深入的理解，同時(shí)能夠準(zhǔn)確地把握問題的關(guān)鍵所在，從而選擇合適的逆向思維角度．

2 運(yùn)用逆向思維法求解末速度為零的勻減速直線運(yùn)動(dòng)

例1 一輛汽車以6m/s的速度沿平直公路勻速行駛，突然發(fā)現(xiàn)前方有障礙物，于上立即剎車，汽車以大小為2m/s2的加速度做勻減速直線運(yùn)動(dòng)，則下面說法正確的是（ ）

（A）第1s內(nèi)與第3s內(nèi)的位移之差3m．

（B）剎車的整個(gè)過程平均速度大小為3m/s．

（C）剎車后1s內(nèi)與剎車后4s內(nèi)汽車通過的位移之比為5∶8．

（D）剎車的第1s內(nèi)、第2s內(nèi)、第3s內(nèi)的位移之比為3∶2∶1．

解析 根據(jù)逆向思維，汽車從剎車到停止的時(shí)間為t0=v0a=3s，則從剎車到停止的位移為x=v202a=9m，剎車的整個(gè)過程平均速度大小為v=93m/s=3m/s，故（B）正確；

根據(jù)逆向思維，汽車反向做初速度為零的勻加速直線運(yùn)動(dòng)，結(jié)合上述可知，剎車的第1s內(nèi)、第2s內(nèi)、第3s內(nèi)的位移之比為5∶3∶1，故（D）錯(cuò)誤；

結(jié)合上述可知，剎車后第1s內(nèi)的位移為5m，第2s內(nèi)的位移為3m，第3s內(nèi)的位移為1m，可知，第1s內(nèi)與第3s內(nèi)的位移之差4m，故（A）錯(cuò)誤；

結(jié)合上述可知，剎車后第1s內(nèi)的位移為5m，剎車時(shí)間為3s，則剎車后4s內(nèi)位移為9m，則汽車剎車后1s內(nèi)與剎車后4s內(nèi)汽車通過的位移之比為5∶9，故（C）錯(cuò)誤．

點(diǎn)評(píng) 在勻變速直線運(yùn)動(dòng)中，在計(jì)算位移大小和時(shí)間時(shí)，為了方便計(jì)算，運(yùn)用逆向思維可將末速度為零的勻減速直線運(yùn)動(dòng)看作初速度為零的勻加速直線運(yùn)動(dòng)來處理，可大大降低分析問題的難度和簡(jiǎn)化計(jì)算的過程[2]．

3 運(yùn)用逆向思維法求解斜上拋運(yùn)動(dòng)問題

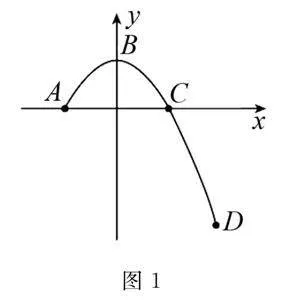
例2 某校秋季運(yùn)動(dòng)會(huì)分為競(jìng)技組和健身組，健身組設(shè)置了定點(diǎn)投籃項(xiàng)目．某選手正在進(jìn)行定點(diǎn)投籃，籃球在空中劃出了一道漂亮的弧線．在籃球運(yùn)動(dòng)所在的豎直平面內(nèi)建立坐標(biāo)系xOy，如圖1所示，籃球由A點(diǎn)被投出，A、B、C、D是籃球運(yùn)動(dòng)軌跡上的四點(diǎn)，B為籃球運(yùn)動(dòng)的最高點(diǎn)，A、B、C、D四點(diǎn)的坐標(biāo)分別為－L，0，0，L、L，0、2L，y，重力加速度為g，空氣阻力忽略不計(jì)．則下列說法正確的是（ ）

（A）籃球經(jīng)過A、C兩點(diǎn)時(shí)速度相同．

（B）籃球經(jīng)過B點(diǎn)時(shí)速度大小為gL．

（C）籃球從A到B與B到C過程中，速度變化相同．

（D）D點(diǎn)的縱坐標(biāo)y=－3L．

解析 依題意，可知籃球拋出后做斜上拋運(yùn)動(dòng)，利用逆向思維，可知籃球從B點(diǎn)做平拋運(yùn)動(dòng)到A點(diǎn)，由圖1知，A點(diǎn)和C點(diǎn)在同一水平線上，則可知籃球在兩點(diǎn)處的速度大小相等，但方向不同，所以兩點(diǎn)處的速度不相同，故（A）錯(cuò)誤；

利用逆向思維，籃球從B點(diǎn)到A點(diǎn)做平拋運(yùn)動(dòng)，設(shè)運(yùn)動(dòng)時(shí)間為t，則有L=vBt，L=12gt2，聯(lián)立解得vB=gL2，故（B）錯(cuò)誤；

根據(jù)Δv=gΔt，可知籃球從A到B與B到C過程中，水平方向上發(fā)生的位移相等，運(yùn)動(dòng)時(shí)間相等，因此速度變化相同，故（C）正確；

籃球由B到D，由圖5可得y－L=gt2，L=vBt，vB=gL2，聯(lián)立解得y=3L，因此D點(diǎn)的縱坐標(biāo)為y=－3L，故（D）正確．

點(diǎn)評(píng) 在高考中，斜上拋運(yùn)動(dòng)只做定性分析，不做定量計(jì)算要求，但因斜上拋運(yùn)動(dòng)的軌跡為拋物線，可將圖像沿著對(duì)稱軸分開，兩邊對(duì)稱，可看作平拋運(yùn)動(dòng)來處理，即物體從拋出點(diǎn)到最高點(diǎn)運(yùn)動(dòng)的過程，可以利用逆向思維法，看成平拋運(yùn)動(dòng)來分析．

4 結(jié)語

綜上所述，逆向思維法在高中力學(xué)解題中具有重要的應(yīng)用價(jià)值．通過運(yùn)用逆向思維法，學(xué)生能夠簡(jiǎn)化問題，提高解題效率和準(zhǔn)確性，培養(yǎng)創(chuàng)新思維能力[3].在高中物理教學(xué)中，教師應(yīng)注重培養(yǎng)學(xué)生的逆向思維能力，引導(dǎo)學(xué)生靈活運(yùn)用逆向思維法解決物理問題，從而提高學(xué)生的物理學(xué)習(xí)能力和綜合素質(zhì)．

參考文獻(xiàn)：

[1]周金金.逆向思維法求解高中物理拋體問題[J].數(shù)理天地（高中版），2024（12）：41-42.

[2]廖榮.利用逆向思維妙解物理問題[J].數(shù)理天地（高中版），2024（06）：17-18.

[3]劉建偉.高中物理教學(xué)中學(xué)生逆向思維的培養(yǎng)策略研究[J].家長(zhǎng)，2023（21）：165-167.