非質點類機械能守恒問題的解題策略

【摘要】本文深入探討非質點類機械能守恒問題，詳細闡述“液柱”類模型、“軟繩”類模型和“鏈條”類模型的機械能守恒問題及相應的解題策略．通過對各種典型實例的分析，強調正確選擇系統、細致分析能量轉化、準確判斷守恒條件以及合理運用相關物理量的重要性．旨在為解決非質點類機械能守恒問題提供有效的方法和思路，以提升對該類問題的理解和處理能力．

【關鍵詞】機械能守恒；高中物理；解題策略

機械能守恒定律是物理學中的重要定律之一，在解決眾多物理問題中具有關鍵作用．然而，當涉及到非質點類物體時，問題的復雜性增加，需要特定的策略和方法來準確求解．對非質點類機械能守恒問題的深入研究具有重要的理論和實踐意義．

1 “液柱”類模型中的機械能守恒問題

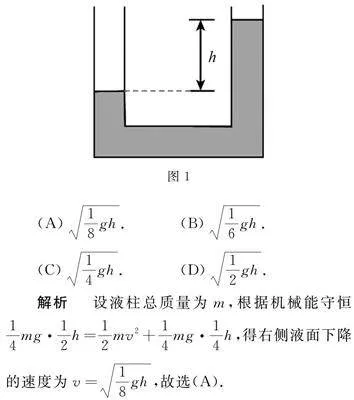
例1 如圖1所示，粗細均勻、兩端開口的U形管內裝有同種液體，管中液柱總長度為4h，開始時使兩邊液面高度差為h，后來讓液體自由流動，當兩液面高度相等時，右側液面下降的速度為（ ）

（A）18gh. （B）16gh.

（C）14gh.（D）12gh.

解析 設液柱總質量為m，根據機械能守恒14mg·12h=12mv2+14mg·14h，得右側液面下降的速度為v=18gh，故選（A）．

解題策略 運用機械能守恒定律解決“液柱”類模型問題時，確定重力勢能是關鍵，需要分段確定其重心和質量，進而確定重力勢能．

2 “軟繩”類模型中的機械能守恒問題

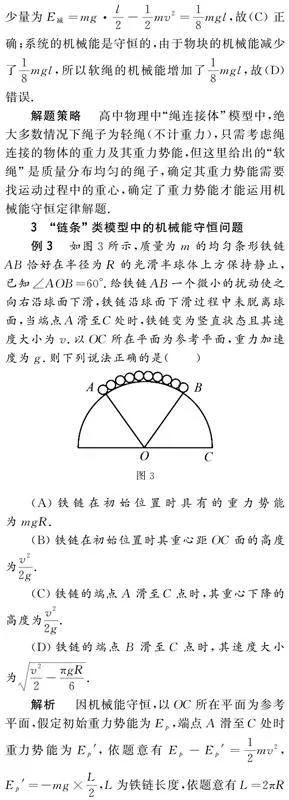
例2 如圖2所示，總長為l、質量為m的均勻軟繩對稱地掛在輕小滑輪上，用細線將質量也為m的物塊與軟繩一端連接．現將物塊由靜止釋放，直到軟繩剛好全部離開滑輪．不計一切摩擦，重力加速度為g，下列說法正確的是（ ）

（A）剛釋放物塊時，細線的拉力大小等于mg.

（B）在軟繩從靜止到剛離開滑輪的過程中，軟繩的機械能守恒.

（C）在軟繩從靜止到剛離開滑輪的過程中，物塊的機械能減少了18mgl.

（D）在軟繩從靜止到剛離開滑輪的過程中，軟繩的機械能增加了38mgl.

解析 剛釋放的時候，物塊是有向下的加速度的，根據牛頓第二定律有mg－T=ma，可知拉力小于mg，故（A）錯誤；在軟繩從靜止到剛離開滑輪的過程中，拉力對軟繩做了功，軟繩機械能不守恒，故（B）錯誤；設軟繩剛離開滑輪的時候，物塊和軟繩的速度為v，根據機械能守恒定律有mg·l2+mg2·l2=12·2m·v2，計算可得v=3gl2，則物塊機械能的減少量為E減=mg·l2－12mv2=18mgl，故（C）正確；系統的機械能是守恒的，由于物塊的機械能減少了18mgl，所以軟繩的機械能增加了18mgl，故（D）錯誤．

解題策略 高中物理中“繩連接體”模型中，絕大多數情況下繩子為輕繩（不計重力），只需考慮繩連接的物體的重力及其重力勢能，但這里給出的“軟繩”是質量分布均勻的繩子，確定其重力勢能需要找運動過程中的重心，確定了重力勢能才能運用機械能守恒定律解題．

3 “鏈條”類模型中的機械能守恒問題

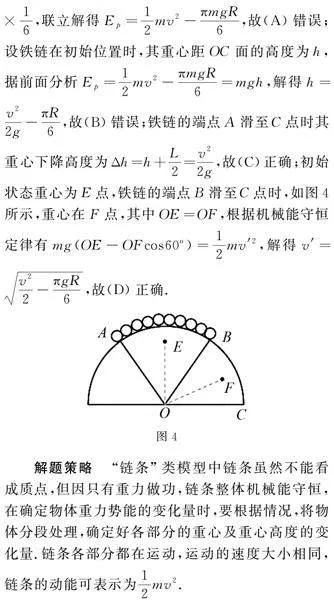
例3 如圖3所示，質量為m的均勻條形鐵鏈AB恰好在半徑為R的光滑半球體上方保持靜止，已知∠AOB=60°．給鐵鏈AB一個微小的擾動使之向右沿球面下滑，鐵鏈沿球面下滑過程中未脫離球面，當端點A滑至C處時，鐵鏈變為豎直狀態且其速度大jugTL0i9dcsZPIcjx1seQQ==小為v．以OC所在平面為參考平面，重力加速度為g．則下列說法正確的是（ ）

（A）鐵鏈在初始位置時具有的重力勢能為mgR.

（B）鐵鏈在初始位置時其重心距OC面的高度為v22g.

（C）鐵鏈的端點A滑至C點時，其重心下降的高度為v22g.

（D）鐵鏈的端點B滑至C點時，其速度大小為v22－πgR6.

解析 因機械能守恒，以OC所在平面為參考平面，假定初始重力勢能為Ep，端點A滑至C處時重力勢能為Ep′，依題意有Ep－Ep′=12mv2，Ep′=－mg×L2，L為鐵鏈長度，依題意有L=2πR×16，聯立解得Ep=12mv2－πmgR6，故（A）錯誤；設鐵鏈在初始位置時，其重心距OC面的高度為h，據前面分析Ep=12mv2－πmgR6=mgh，解得h=v22g－πR6，故（B）錯誤；鐵鏈的端點A滑至C點時其重心下降高度為Δh=h+L2=v22g，故（C）正確；初始狀態重心為E點，鐵鏈的端點B滑至C點時，如圖4所示，重心在F點，其中OE=OF，根據機械能守恒定律有mg（OE－OFcos60o）=12mv′2，

解得v′=v22－πgR6，故（D）正確．

解題策略 “鏈條”類模型中鏈條雖然不能看成質點，但因只有重力做功，鏈條整體機械能守恒，在確定物體重力勢能的變化量時，要根據情況，將物體分段處理，確定好各部分的重心及重心高度的變化量．鏈條各部分都在運動，運動的速度大小相同，鏈條的動能可表示為12mv2．

4 結語

非質點類機械能守恒問題雖然具有一定的復雜性，但通過合理的解題策略，可以有效地進行分析和求解．對系統的恰當選擇、深入的能量分析、準確的守恒條件判斷以及合理的物理量運用是解決此類問題的關鍵．進一步地研究和實踐將有助于更深入地理解和掌握這些策略，從而更好地處理各種復雜的物理問題．

參考文獻：

[1]陳衛國.“遷移法”解非質點類機械能守恒問題[J].物理教師，2023，44（06）：96-97.

[2]丁軍濤.善用機械能守恒，化繁為簡有奇功——例析機械能守恒定律在解題中的應用[J].數理天地（高中版），2022（22）：44-46.

[3]鄭周博，勞荊華.回視典例 遷移模型——談一道繩索問題的另解[J].湖南中學物理，2024，39（03）：75-77.