“不變性”作為十二音系統(tǒng)的邏輯鏈

摘 要：不變性，是十二音序列在變化時(shí)保持不變的音樂(lè)特征或關(guān)系。文章提出米爾頓·巴比特的“不變性”理論——包括移位不變性與倒影不變性，對(duì)他的十二音系統(tǒng)創(chuàng)作起到?jīng)Q定性邏輯作用。同時(shí)，在巴比特的晚期創(chuàng)作中，尤其在大型矩陣復(fù)合式作品中也對(duì)音高組織的細(xì)節(jié)處理表現(xiàn)出不同的“不變性”的結(jié)構(gòu)思維。

關(guān)鍵詞：不變性；十二音；米爾頓·巴比特；矩陣

中圖分類號(hào)：J614 文獻(xiàn)標(biāo)識(shí)碼： A 文章編號(hào)：1004 - 2172（2024）04-0123-10

DOI：10.15929/j.cnki.1004 - 2172.2024.04.016

十二音作曲系統(tǒng)在性質(zhì)和含義上是真正具有“革命性”程度的，就如同任何抽象模型完滿的公式化系統(tǒng)一樣，十二音系統(tǒng)可以通過(guò)要素的陳述、內(nèi)部的關(guān)系來(lái)完整地描述音樂(lè)特征，并對(duì)相關(guān)音樂(lè)元素設(shè)定相應(yīng)操作。在這個(gè)作曲程序中，作曲家使用這種“公式化系統(tǒng)”進(jìn)行非公式化處理，所得到的某種“不變性”，是本文分析研究的重要焦點(diǎn)。約瑟夫·施特勞斯 （Joseph Straus）在教科書《后調(diào)性理論導(dǎo)論》（An Introduction to Post-Tonal Theory） 中這樣定義“不變性”：十二音作品中的序列不管進(jìn)行何種移位變型組合排列，總能辨識(shí)出一些保持不變的音樂(lè)特征或關(guān)系[1]。米爾頓·巴比特（Milton Babbitt）更是認(rèn)為“不變性”是十二音作品的決定性作曲技術(shù)。

一、“不變性”的決定性因素

巴比特在對(duì)“不變性”理論的研究文章《不變性是十二音作曲的決定性因素》[2]中，圍繞勛伯格《第三弦樂(lè)四重奏》（Op.30）及韋伯恩《鋼琴變奏曲》（Op.27，第二樂(lè)章）兩個(gè)例子，分別說(shuō)明原型序列與移位序列間，以及互為倒影形式序列間的不變性特征及產(chǎn)生的邏輯關(guān)系。這種邏輯關(guān)系，正是“不變性”的決定性因素，即移位不變性與倒影不變性。

（一）移位不變性

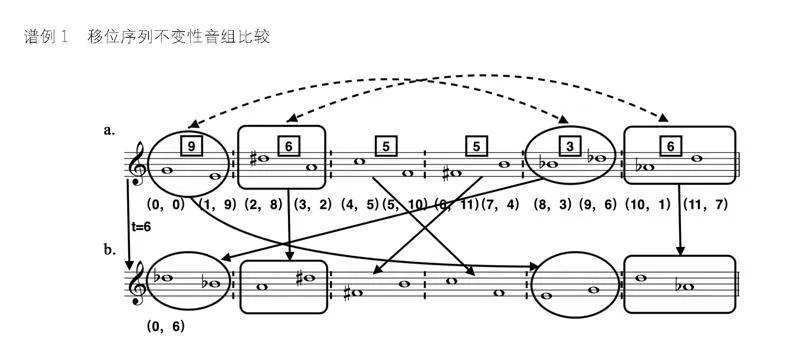
十二音系統(tǒng)中首先需要考慮的是排列性質(zhì)，移位會(huì)導(dǎo)致原始序列中不存在的音高相鄰，從而建立一個(gè)新的子集并導(dǎo)致元素的置換。“傳統(tǒng)”作曲意義上的移位，即移調(diào)，意味著基本輪廓的保留。從字面上講，將移位定義為十二音系統(tǒng)內(nèi)的一項(xiàng)變化形式是毫無(wú)意義的，因?yàn)檩喞且魳?lè)元素獨(dú)特音區(qū)的表現(xiàn)功能，音區(qū)與音長(zhǎng)、音強(qiáng)、音色或與作曲表現(xiàn)必然相關(guān)的任何其他屬性一樣不受集合結(jié)構(gòu)的定義。由于這種限定很容易導(dǎo)致十二音系統(tǒng)原理與作曲容許性（即“一個(gè)序列可以用任何八度表示”）之間的混淆，因此，更有效的方法是用數(shù)字符號(hào)、有序數(shù)對(duì)的標(biāo)記來(lái)體現(xiàn)移位變化：數(shù)對(duì)中的第一個(gè)成員表示該音所處序列中的位置，第二個(gè)成員表示音高級(jí)的“音高號(hào)”。巴比特正是利用這種方式定義了勛伯格《第三弦樂(lè)四重奏》（Op.30）的原型序列（見譜例1）。

任何序列的移位可以通過(guò)將整數(shù)0 —11添加到集合的每個(gè)音高數(shù)來(lái)表示。如果 （a，b） 是表示P序列的某一元素，則移位t后該元素變?yōu)?（a，b+t） ，其中t為“移位數(shù)”。 因此，序列的移位值則被視為對(duì)音高數(shù)的操作與排列。與給定P序列相關(guān)的十二個(gè)移位序列的總和構(gòu)成一個(gè)組合群，憑借生成的群結(jié)構(gòu)，以及源自該組群的交換和傳遞性質(zhì)，可以推導(dǎo)出與序列移位相關(guān)的附加屬性。由于每個(gè)t值都會(huì)導(dǎo)致序列元素的完全紊亂，卻又有著相同的音程順序，因此在尋找移位組合層次化標(biāo)準(zhǔn)時(shí)，這些屬性都不能作為區(qū)分的基礎(chǔ)。同樣，移位的每一個(gè)值都定義了一個(gè)常規(guī)置換，但隨著互補(bǔ)t（和為0的數(shù)字，模12）與只有這樣的t產(chǎn)生相同順序的倒影置換，區(qū)分的不變性基礎(chǔ)出現(xiàn)了。這些屬性其中的不變量（在移位操作下保留的集合屬性，以及集合之間的某些關(guān)系），可以視為十二音系統(tǒng)中的“不變性”結(jié)構(gòu)，需要在音高集合以及音程集合上具有同一性的能力。互補(bǔ)的移位算子對(duì)原型序列來(lái)說(shuō)，會(huì)產(chǎn)生相同數(shù)量的音級(jí)鄰接，包括有序鄰接和反向鄰接。如果一個(gè)序列的a和b、c和d表示處于連續(xù)序號(hào)位置的音集，如果移位算子為t，而a+t=c，b+t=d，那么在t的移位下，a和b與處于原型序列位置中的c和d相關(guān)聯(lián)；在12-t的移位下，c和d與處于原型序列位置的a和b相關(guān)聯(lián)。原型序列的音程結(jié)構(gòu)決定了在特定移位算子及其補(bǔ)碼下保留的不變鄰接組，這個(gè)數(shù)字來(lái)源于原型序列中具有功能性與多重性的互補(bǔ)音程數(shù)。

例如，將譜例1a的序列按照相鄰關(guān)系兩兩一組，分成六個(gè)相鄰二音組：（0，0）與（1，9）；（2，8）與（3，2）；（4，5）與（5，10）；（6，11）與（7，4）；（8，3）與（9，6）；（10，1）與（11，7），這六個(gè)二音組的內(nèi)部音程關(guān)系（半音數(shù)）為[965536]。由此，第三組與第四組各自內(nèi)部的音程距離均為5，而兩組之間的音程距離是6；第一組和第五組各自內(nèi)部的音程距離為互補(bǔ)的9和3，而兩組之間的音程距離也是6；除此之外，第二組和第六組各自內(nèi)部的音程距離均為6。因而，將該序列進(jìn)行t=6的移位操作（見譜例1b），同樣進(jìn)行相鄰二音組的劃分，這六個(gè)音組分別與原型序列保持了相應(yīng)的不變性。以原型序列二音組為參照，T6序列出現(xiàn)的六個(gè)音組順序?yàn)榈谖褰M、第二組、第四組、第三組、第一組、第六組，音程距離為6的兩組在t=6的移位下互換，而本身內(nèi)部音程距離為6的音組保持不變。這體現(xiàn)了利用序列移位形式擴(kuò)展到序列元素保持不變性的有效手段。

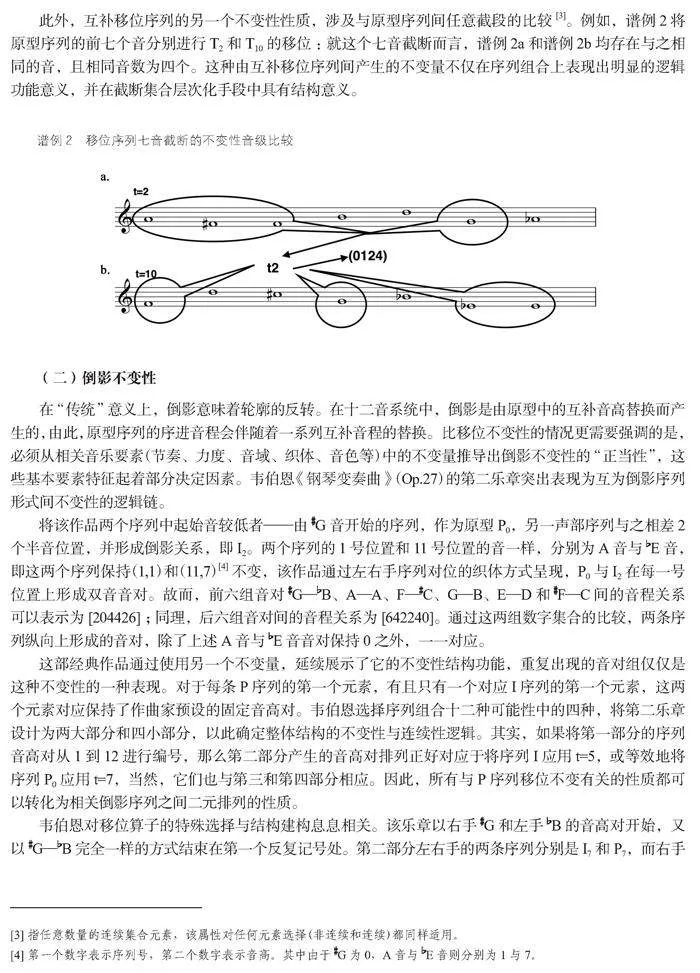
此外，互補(bǔ)移位序列的另一個(gè)不變性性質(zhì)，涉及與原型序列間任意截段的比較[3]。例如，譜例2將原型序列的前七個(gè)音分別進(jìn)行T2和T10的移位：就這個(gè)七音截?cái)喽裕V例2a和譜例2b均存在與之相同的音，且相同音數(shù)為四個(gè)。這種由互補(bǔ)移位序列間產(chǎn)生的不變量不僅在序列組合上表現(xiàn)出明顯的邏輯功能意義，并在截?cái)嗉蠈哟位侄沃芯哂薪Y(jié)構(gòu)意義。

（二）倒影不變性

在“傳統(tǒng)”意義上，倒影意味著輪廓的反轉(zhuǎn)。在十二音系統(tǒng)中，倒影是由原型中的互補(bǔ)音高替換而產(chǎn)生的，由此，原型序列的序進(jìn)音程會(huì)伴隨著一系列互補(bǔ)音程的替換。比移位不變性的情況更需要強(qiáng)調(diào)的是，必須從相關(guān)音樂(lè)要素（節(jié)奏、力度、音域、織體、音色等）中的不變量推導(dǎo)出倒影不變性的“正當(dāng)性”，這些基本要素特征起著部分決定因素。韋伯恩《鋼琴變奏曲》（Op.27）的第二樂(lè)章突出表現(xiàn)為互為倒影序列形式間不變性的邏輯鏈。

將該作品兩個(gè)序列中起始音較低者——由G音開始的序列，作為原型P0，另一聲部序列與之相差2個(gè)半音位置，并形成倒影關(guān)系，即I2。兩個(gè)序列的1號(hào)位置和11號(hào)位置的音一樣，分別為A音與E音，即這兩個(gè)序列保持（1，1）和（11，7）[4]不變，該作品通過(guò)左右手序列對(duì)位的織體方式呈現(xiàn)，P0與I2在每一號(hào)位置上形成雙音音對(duì)。故而，前六組音對(duì)G—B、A—A、F—C、G—B、E—D和F—C間的音程關(guān)系可以表示為[204426]；同理，后六組音對(duì)間的音程關(guān)系為[642240]。通過(guò)這兩組數(shù)字集合的比較，兩條序列縱向上形成的音對(duì)，除了上述A音與E音音對(duì)保持0之外，一一對(duì)應(yīng)。

這部經(jīng)典作品通過(guò)使用另一個(gè)不變量，延續(xù)展示了它的不變性結(jié)構(gòu)功能，重復(fù)出現(xiàn)的音對(duì)組僅僅是這種不變性的一種表現(xiàn)。對(duì)于每條P序列的第一個(gè)元素，有且只有一個(gè)對(duì)應(yīng)I序列的第一個(gè)元素，這兩個(gè)元素對(duì)應(yīng)保持了作曲家預(yù)設(shè)的固定音高對(duì)。韋伯恩選擇序列組合十二種可能性中的四種，將第二樂(lè)章設(shè)計(jì)為兩大部分和四小部分，以此確定整體結(jié)構(gòu)的不變性與連續(xù)性邏輯。其實(shí)，如果將第一部分的序列音高對(duì)從1到12進(jìn)行編號(hào)，那么第二部分產(chǎn)生的音高對(duì)排列正好對(duì)應(yīng)于將序列I應(yīng)用t=5，或等效地將序列P0應(yīng)用t=7，當(dāng)然，它們也與第三和第四部分相應(yīng)。因此，所有與P序列移位不變有關(guān)的性質(zhì)都可以轉(zhuǎn)化為相關(guān)倒影序列之間二元排列的性質(zhì)。

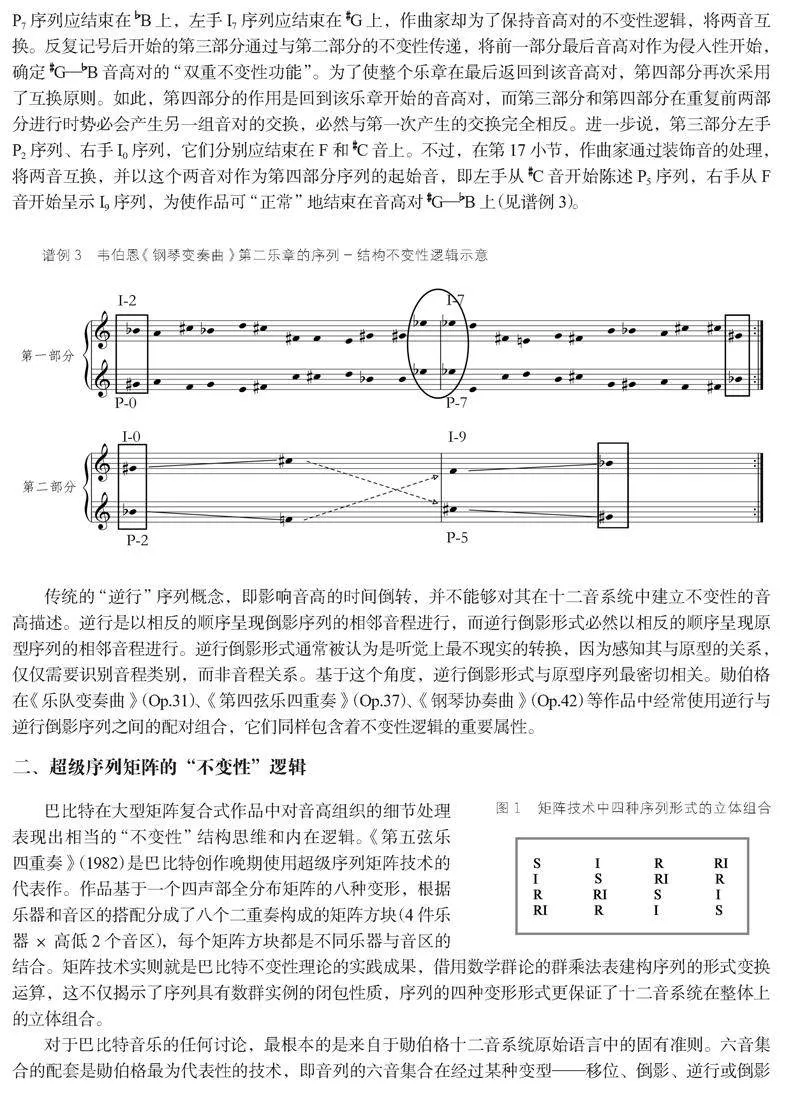
韋伯恩對(duì)移位算子的特殊選擇與結(jié)構(gòu)建構(gòu)息息相關(guān)。該樂(lè)章以右手G和左手B的音高對(duì)開始，又以G—B完全一樣的方式結(jié)束在第一個(gè)反復(fù)記號(hào)處。第二部分左右手的兩條序列分別是I7和P7，而右手P7序列應(yīng)結(jié)束在B上，左手I7序列應(yīng)結(jié)束在G上，作曲家卻為了保持音高對(duì)的不變性邏輯，將兩音互換。反復(fù)記號(hào)后開始的第三部分通過(guò)與第二部分的不變性傳遞，將前一部分最后音高對(duì)作為侵入性開始，確定G—B音高對(duì)的“雙重不變性功能”。為了使整個(gè)樂(lè)章在最后返回到該音高對(duì)，第四部分再次采用了互換原則。如此，第四部分的作用是回到該樂(lè)章開始的音高對(duì)，而第三部分和第四部分在重復(fù)前兩部分進(jìn)行時(shí)勢(shì)必會(huì)產(chǎn)生另一組音對(duì)的交換，必然與第一次產(chǎn)生的交換完全相反。進(jìn)一步說(shuō)，第三部分左手P2序列、右手I0序列，它們分別應(yīng)結(jié)束在F和C音上。不過(guò)，在第17小節(jié)，作曲家通過(guò)裝飾音的處理，將兩音互換，并以這個(gè)兩音對(duì)作為第四部分序列的起始音，即左手從C音開始陳述P5序列，右手從F音開始呈示I9序列，為使作品可“正常”地結(jié)束在音高對(duì)G—B上（見譜例3）。

傳統(tǒng)的“逆行”序列概念，即影響音高的時(shí)間倒轉(zhuǎn)，并不能夠?qū)ζ湓谑粝到y(tǒng)中建立不變性的音高描述。逆行是以相反的順序呈現(xiàn)倒影序列的相鄰音程進(jìn)行，而逆行倒影形式必然以相反的順序呈現(xiàn)原型_{2029b2f7e36b20342acd6e7ebce05e98}序列的相鄰音程進(jìn)行。逆行倒影形式通常被認(rèn)為是聽覺(jué)上最不現(xiàn)實(shí)的轉(zhuǎn)換，因?yàn)楦兄渑c原型的關(guān)系，僅僅需要識(shí)別音程類別，而非音程關(guān)系。基于這個(gè)角度，逆行倒影形式與原型序列最密切相關(guān)。勛伯格在《樂(lè)隊(duì)變奏曲》（Op.31）、《第四弦樂(lè)四重奏》（Op.37）、《鋼琴協(xié)奏曲》（Op.42）等作品中經(jīng)常使用逆行與逆行倒影序列之間的配對(duì)組合，它們同樣包含著不變性邏輯的重要屬性。

二、超級(jí)序列矩陣的“不變性”邏輯

巴比特在大型矩陣復(fù)合式作品中對(duì)音高組織的細(xì)節(jié)處理表現(xiàn)出相當(dāng)?shù)摹安蛔冃浴苯Y(jié)構(gòu)思維和內(nèi)在邏輯。《第五弦樂(lè)四重奏》（1982）是巴比特創(chuàng)作晚期使用超級(jí)序列矩陣技術(shù)的代表作。作品基于一個(gè)四聲部全分布矩陣的八種變形，根據(jù)樂(lè)器和音區(qū)的搭配分成了八個(gè)二重奏構(gòu)成的矩陣方塊（4件樂(lè)

器×高低2個(gè)音區(qū)），每個(gè)矩陣方塊都是不同樂(lè)器與音區(qū)的結(jié)合。矩陣技術(shù)實(shí)則就是巴比特不變性理論的實(shí)踐成果，借用數(shù)學(xué)群論的群乘法表建構(gòu)序列的形式變換運(yùn)算，這不僅揭示了序列具有數(shù)群實(shí)例的閉包性質(zhì)，序列的四種變形形式更保證了十二音系統(tǒng)在整體上的立體組合。

對(duì)于巴比特音樂(lè)的任何討論，最根本的是來(lái)自于勛伯格十二音系統(tǒng)原始語(yǔ)言中的固有準(zhǔn)則。六音集合的配套是勛伯格最為代表性的技術(shù)，即音列的六音集合在經(jīng)過(guò)某種變型——移位、倒影、逆行或倒影逆行之后形成與之互補(bǔ)的六音集合。《第五弦樂(lè)四重奏》所使用的序列原型由兩個(gè)E型六音集合[5]組成，對(duì)原型序列P0〈0378e42619t5〉的分析可得，前六個(gè)音級(jí)與后六個(gè)音級(jí)都是以“4”為邏輯關(guān)系循環(huán)而成[6]。E型六音集合，即集合6-20（014589）作為該序列的核心集合，除了上述的三音集合（048）的不變性傳遞之外，其有限子集使得某些特定音集形成音序截?cái)嗟亩鄻又貜?fù)。另外，序列架構(gòu)本身體現(xiàn)出“不變性”邏輯思維，如譜例4分割所得的三音集合截?cái)啵?-11（037）與集合3-4（015）分別構(gòu)成前后六音組的順序三音截?cái)啵疫@兩個(gè)集合又各自交換音組出現(xiàn)在相同位置，而集合3-3（014）在兩個(gè)音組中保持2-4號(hào)的對(duì)稱位置。

（一）移位不變性的序列指數(shù)關(guān)系

巴比特將勛伯格的序列以相鄰兩音為一組，并通過(guò)比較組內(nèi)音程距離得到了“6”關(guān)系下的移位不變性。在巴比特的原型序列中，六個(gè)相鄰二音組[8]間的二元音程關(guān)系（半音數(shù)）為[315487]，其中，第三組與第六組、第四組與第五組的內(nèi)部音程差為互補(bǔ)關(guān)系[9]。首先，P0與P6[10]之間的不變性關(guān)系表現(xiàn)為第三組與第六組的（5，t）（4，e）和P0互換了位置，且P6的（8，7）（9，3）與P0的（1，3）（2，7）呼應(yīng)，P0的（8，1）（9，9）與P6的（1，9）（2，1）呼應(yīng)。在P6下已經(jīng)形成了四個(gè)與P0相互呼應(yīng)的二音組不變性關(guān)系，而剩下的四號(hào)音[11]也存在著不變性映射。不僅兩個(gè)序列所剩未呼應(yīng)的序號(hào)位置相同，且是單音呼應(yīng)的。由于這樣的不變性呼應(yīng)，兩個(gè)序列實(shí)際上是移位配套序列，即P0序列的前六音與P6序列的前六音共同組成完整的十二音集合，后六音組亦然（見譜例5）。

P2與Pt均為P0的移位配套序列，另也存在一種“不變性”序列，它們的前后六音組相同，即P4與P8序列是P0的“相同”序列。移位序列可分為兩組：配套組和相同組，觀察兩組序列的指數(shù)，配套組的P2-6-t與相同組的P0-4-8均建立在以“4”為基數(shù)的循環(huán)關(guān)系。這種“4”的循環(huán)關(guān)系不僅是巴比特架構(gòu)序列的邏輯核心，還成了一種不變性的序列選擇邏輯鏈，即公式化表示為Invariant[P0-Px] →[Px=Px+4n]（n為1，2，3）。

（二）倒影不變性的序列指數(shù)關(guān)系

《第五弦樂(lè)四重奏》原型序列的核心三音集合3-3（014）、3-4（015）和3-11（037）分別作為非離散三音集合出現(xiàn)在序列前后兩個(gè)六音截?cái)嘀懈饕淮巍＜希?14）分別在P2與Pt下互相映射，集合（015）與（037）則是通過(guò)倒影關(guān)系呈現(xiàn)不變性。而序列前后六音組中分別出現(xiàn)的三個(gè)核心四音集合4-17（0347）、4-19（0148）與4-20（0158）也同樣在倒影I5與I9關(guān)系中體現(xiàn)著不變性。這里，I5與I9的指數(shù)又出現(xiàn)了“4”關(guān)系，按照此邏輯鏈推理，I1勢(shì)必與P0存在某種倒影等同關(guān)系，或I1一定與I5、I9存在某種不變性關(guān)系。

根據(jù)巴比特對(duì)韋伯恩作品倒影序列不變性的研究，兩條互為倒影關(guān)系的序列以縱向上形成的二音對(duì)作為不變性形態(tài)貫穿。如果將指數(shù)“4”關(guān)系代入巴比特的P0序列，I7、Ie序列與其在相同序號(hào)位置上形成的縱向二音對(duì)在其他位置上保持不變性，構(gòu)成倒影不變性序列關(guān)系。按照移位不變性序列的指數(shù)公式帶入，與P序列形成如此關(guān)系的倒影序列間的指數(shù)關(guān)系可以類比為公式Px=Ix+3+4n（n=0，1，2）。因而，倒影序列間同樣存在指數(shù)為“4”循環(huán)的不變性邏輯鏈。

序列I5、I9與P0除了上述的音列局部不變性之外，它們還是P0的倒影配套序列，即它們的前后六音組與P0為配套關(guān)系，P1亦然。因此，與P序列形成配套關(guān)系的倒影序列間的指數(shù)關(guān)系可以類比為Px=

Ix+1+4n（n=0，1，2）。該作品序列選擇邏輯除了以上分析所得的“4”循環(huán)之外，最核心的“不變性”邏輯鏈?zhǔn)抢没榈褂芭涮椎男蛄羞M(jìn)行，這也是巴比特矩陣技術(shù)的靈魂所在，由此形成橫向上兩條互為倒影關(guān)系的音列有序呈示，縱向上兩個(gè)互補(bǔ)六音集合“塊狀”呈示的音響效果。

以第一超級(jí)序列矩陣呈示的四個(gè)矩陣為例來(lái)研究序列指數(shù)關(guān)系，四個(gè)音層在呈示八個(gè)分割組下的序列進(jìn)行可以分為兩組配套關(guān)系：音層1-2的一對(duì)序列指數(shù)間關(guān)系為（+1，+5，+5，+5，+5，+5，+5，+1）；而音層3-4的一對(duì)序列指數(shù)間關(guān)系為（+1，+9，+5，+9，+9，+9，+1，+5）。因此，縱向音層對(duì)之間的一對(duì)倒影配套序列，可以用公式表示指數(shù)Px=Ix+1+4n（n=0，1，2）關(guān)系。且在每個(gè)音層的橫向呈示上，同時(shí)仍存在著序列形式的循環(huán)以及指數(shù)“4”循環(huán)的邏輯不變性。如以第一矩陣第一音層為例，分割組H-E分別陳述四種序列形式：R-e、I-4、RI-2和P-1，之后，在分割組D-A再次以這四種序列形式出現(xiàn)順序依次為R-3、I-8、RI-t和P-9，相同序列形式間的指數(shù)關(guān)系均為“4”關(guān)系。因而，由此實(shí)現(xiàn)Invariant（不變）→Non-Invariant（非不變）之“以不變應(yīng)萬(wàn)變，然不變即萬(wàn)變”。（見表1）

（三）四音集合的不變性關(guān)系

巴比特在其另一代表性文章《集合結(jié)構(gòu)作為作曲的一個(gè)決定要素》[12]中指出，在任何作曲系統(tǒng)技術(shù)中保留的集合形式及衍生關(guān)系會(huì)架構(gòu)起作品的獨(dú)特邏輯結(jié)構(gòu)。根據(jù)巴比特對(duì)互補(bǔ)序列不變性的研究，同樣將原型序列與某個(gè)移位序列及它的互補(bǔ)序列的前七音截?cái)嗉线M(jìn)行比較，選擇哪些互補(bǔ)序列做參考系成為了首要問(wèn)題。根據(jù)上文對(duì)移位序列不變性的研究，已知相同形式的序列，在其指數(shù)差為4時(shí)的兩個(gè)序列是保持“不變的”，如P0與P4、P8；而在指數(shù)差為2+4n時(shí)（n=0，1，2）時(shí)，兩個(gè)序列為相同形式的配套序列，如P0與P2、P6和Pt。因此，以下將比較恰好剩下的3組互補(bǔ)序列：P0、Pe，P3、P9和P5、P7之間的不變性。

前提是基于集合思維，從原型序列的核心E型六音集合（014589）中共可以取出15個(gè)四音集合[14]，基本型僅有4種（0145）（0148）（0158）和（0347）。除了（0145）之外，其余三個(gè)都在前后六音截?cái)嘀懈鞒霈F(xiàn)一次。比較得出，P1、Pe與P0的前七音截?cái)嘀胁蛔冃砸艏?jí)分別為集合（0，3，4，8）和（2，3，7，e）[15]，且兩個(gè)四音集合原型均為（0148），并構(gòu)成1個(gè)半音距離的移位關(guān)系。對(duì)余下兩組進(jìn)行相同的操作可得到相同結(jié)果，即每組與P0都產(chǎn)生四個(gè)不變音，且它們均為不變性四音集合（0148）。更甚者，三組互補(bǔ)序列與P0的不變四音集合均有（2，3，7，e），它是P0與Pe、P0與P3、P0與P7形成的不變音。

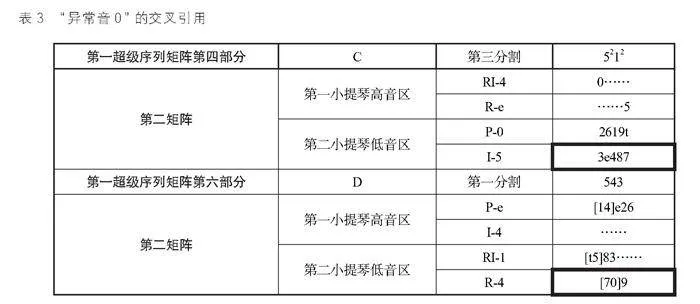
（2，3，7，e）以初始分割單元初次出現(xiàn)在第一矩陣第四音層大提琴高音區(qū)呈示的序列RI0的1—4號(hào)音，如表2所示，BLOCK4（第31—38小節(jié)）是由第一矩陣和第二矩陣共時(shí)展開，并分別呈現(xiàn)分割組H與分割組C。每kdA5ycQfpct5pjw25dhdOPexHbR3F+rUa8pJOC25eo0=個(gè)矩陣共四個(gè)音層，由不同樂(lè)器的不同音區(qū)組合，每個(gè)分割組包括將12音分割進(jìn)四個(gè)音層的四種分割型。由于H分割組的第一個(gè)分割型 43是縱向形成三個(gè)四音集合，（2，3，7，e）即是其中一個(gè)，與此同時(shí)大提琴高音區(qū)的另一序列R-11也呈現(xiàn)前4號(hào)音（4，9，8，0）。若把（2，3，7，e）定義為原型T-0，（4，9，8，0）則是它的倒影等同集合I-e。然而，在進(jìn)行到下一分割型 623時(shí)，大提琴高音區(qū)R11的二音組（5，1）與第一小提琴低音區(qū)I1的二音組（2，9）形成了（2，3，7，e）的倒影等同集合I-4。這兩個(gè)音層同樣在第三分割型5321時(shí)以3+1的形式縱向形成集合（e，7，0，3），它也與（2，3，7，e）形成倒影等同關(guān)系。（2，3，7，e）從開始在大提琴高音區(qū)的兩個(gè)音層橫向陳述，之后以縱向疊合的方式于音層1、3組合形成，且兩次分別為（2+2）與（3+1）的分割形態(tài)。在BLOCK4的最后一個(gè)分割型4222，（2，3，7，e）又回歸到大提琴音層3，這也是R11序列的最后4號(hào)音，以與之I-9關(guān)系結(jié)束。第一矩陣在四個(gè)分割型下保持了（2，3，7，e）的集合不變性貫穿，并且在集合的移位進(jìn)行關(guān)系上又表現(xiàn)出對(duì)稱性，即e-4-2-9。

在BLOCK4僅8小節(jié)的陳述并不只有（2，3，7，e）的集合不變性貫穿這么簡(jiǎn)單。最顯性的不變性還表現(xiàn)在：第一矩陣第一音層的第一個(gè)分割型所形成的四音集合（1t65），在一個(gè)分割型由第三、第四音層組合出現(xiàn)，緊接著，第三、第四音層組合出現(xiàn)的（3814）結(jié)合又交換至第一、二音層組合呈現(xiàn)。這兩個(gè)四音集合的基本型分別是（0158）和（0247），（0158）正是除了（0148）之外的E型六音集合的子集之一。同樣，與第一矩陣在同一方塊同時(shí)進(jìn)行的第二矩陣，第一個(gè)分割型34形成的4個(gè)3音集合，其實(shí)只有兩個(gè)基本型（015）和（037）。其實(shí)第二矩陣不管是縱向的音層組合還是橫向的序列分割，核心就圍繞著這兩個(gè)三音集合以及（0158）與（0347）不變性貫穿。它們與第一矩陣的（0148）集合共同搭建起B(yǎng)LOCK4的不變性結(jié)構(gòu)，同時(shí)也解釋了為什么作曲家沒(méi)有將（0145）作為子集合設(shè)計(jì)在原型序列中，作曲家將其包含的兩個(gè)三音集合當(dāng)作不變性的邏輯鏈，而非以四音集合的形態(tài)[16]。

（四）節(jié)奏不變性解釋的異常音來(lái)源

超級(jí)序列矩陣技術(shù)需要解決多個(gè)矩陣共同展開對(duì)立而形成的豐富音高資源。也許最?yuàn)W妙的地方就是作品中那些不是來(lái)自譜面本身所處矩陣中的音級(jí)而創(chuàng)造出的“異常音”，由基礎(chǔ)矩陣結(jié)構(gòu)的交叉引用產(chǎn)生，并且大大依賴于節(jié)奏特征的有力輔助，也正是作品不變性技術(shù)的細(xì)節(jié)微現(xiàn)。

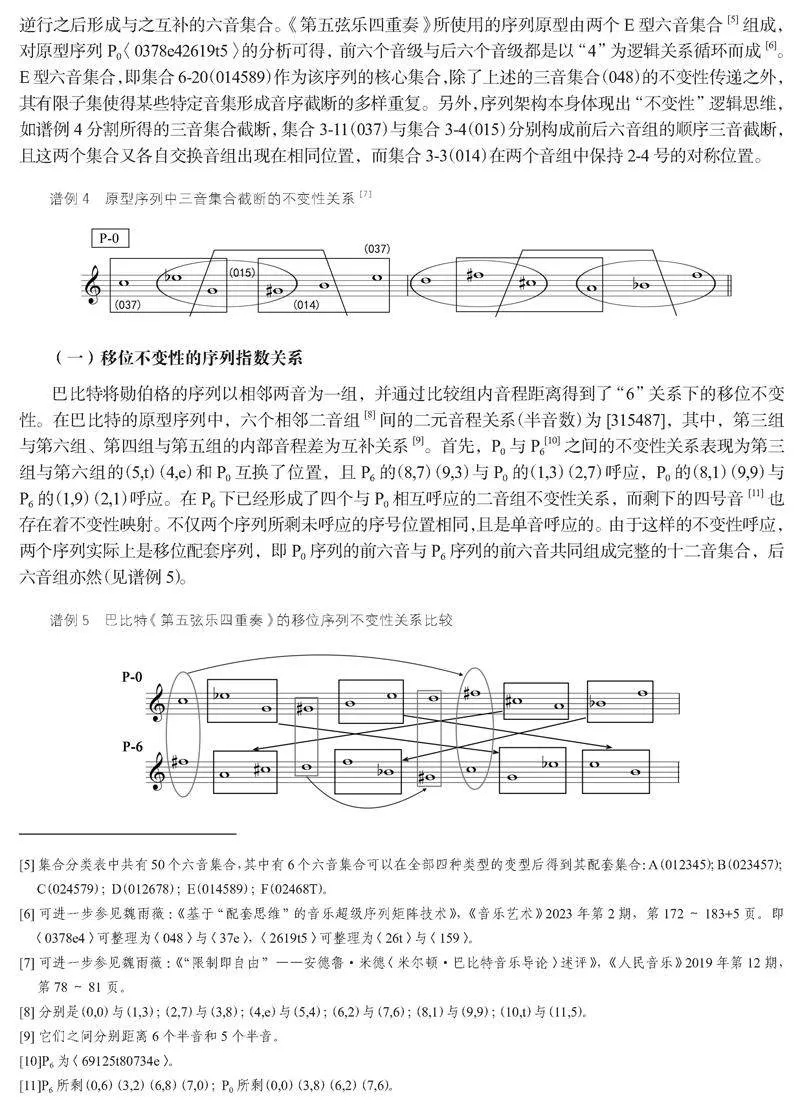
如譜例6所示，該部分參與呈示的矩陣有第一、第二和第四矩陣。例中第一小提琴所示的音級(jí)從bE音開始都可以得到明確的矩陣與序列歸屬，唯獨(dú)第191小節(jié)出現(xiàn)的中央C（“異常音0”）無(wú)法解釋。根據(jù)表3對(duì)第一小提琴在兩個(gè)矩陣的序列所有可用的音級(jí)中進(jìn)行篩選，只有從序列R7中的0音也許可以作為其來(lái)源，但真正屬于此序列的0音在189小節(jié)已經(jīng)出現(xiàn)過(guò)了。事實(shí)上，在巴比特的十二音作品中，對(duì)于“被使用過(guò)的音級(jí)不再使用”這一原則上非常嚴(yán)格，而且這兩個(gè)矩陣四個(gè)序列沒(méi)有列出的余下部分音級(jí)，也沒(méi)有可以解釋這個(gè)不規(guī)則音級(jí)的出現(xiàn)。

通過(guò)對(duì)第一小提琴橫向上形成的旋律截?cái)喾治鰜?lái)看，第190小節(jié)由連音線劃分的三音截?cái)啵?，8，7）以及“異常音0”與重復(fù)7音組成的二音截?cái)啵?，0）是破解來(lái)源的重要線索。通過(guò)在序列陣中找尋這兩個(gè)截?cái)啵蛄蠭5是異常音有力的來(lái)源候補(bǔ)者，它的最后四號(hào)音就是（4，8，7，0）。因此，該“異常音0”就是對(duì)第四部分第二矩陣第二小提琴低音音層4序列I5特定位置的引用。首先，關(guān)于上述兩個(gè)截?cái)嗟膩?lái)源分別是第二矩陣音層4在第四部分第三分割處形成了五音的分割I(lǐng)5（3，e，4，8，7）以及在第六部分第一分割處形成的三音分割I(lǐng)5（7，0）與R4（9）。若沒(méi)有節(jié)奏特征的輔助，上述解釋可能是對(duì)于總體引用的錯(cuò)誤判斷，正是節(jié)奏使得這種特定區(qū)域的來(lái)源變得確定而清晰。第190小節(jié)的（4，8，7）是五連音的第三、四、五部分，在引用的第四部分第二矩陣音層4的第三分割處形成的五音分割中，這三個(gè)音級(jí)相應(yīng)的同樣是在第三、四、五部分。（0，7）是191小節(jié)三連音的第一、二部分，它們也同樣是引用部分實(shí)現(xiàn)三音分割的第一、二部分。而且，音級(jí)7的音高不變性在結(jié)構(gòu)表面也同樣以重復(fù)形式表現(xiàn)出來(lái)。

另一個(gè)這樣的引用發(fā)生在201－202小節(jié)，也是第一超級(jí)序列矩陣的第十四部分，大提琴分為高、低音區(qū)分別屬于第一矩陣和第四矩陣。如譜例7a所示，0音和2音的來(lái)源分別是RI8和R3，而9音（“異常音9”）不規(guī)則出現(xiàn)了。序列RI8確實(shí)有9音，但在 201小節(jié)出現(xiàn)過(guò)了，且是在與“異常音9”不同的八度上。巴比特避免呈現(xiàn)來(lái)源相同的音級(jí)在同一位置的兩個(gè)八度上，因此RI8不可能是“異常音9”的來(lái)源。實(shí)際上這里的引用是來(lái)自第一超級(jí)序列矩陣第十一部分第三矩陣第二小提琴高音聲部音層1的序列Rt。音層1在該部分第一分割處形成了一個(gè)十音的分割，而（0，2，9）出現(xiàn)在第六、七、八號(hào)位置上。第201小節(jié)，這三個(gè)音在五音組的第一、二、三部分代替一個(gè)八分音符。巴比特對(duì)于節(jié)奏的設(shè)計(jì)使得一切合理又巧妙。五連音的前面有兩個(gè)十六分休止，所以休止和五連音按時(shí)值可以被理解為十音組代替一個(gè)四分音符，而這個(gè)十音組的第六、七、八部分是音級(jí)（0，2，9）。并且第137小節(jié)第三矩陣第二小提琴高音聲部音層1的（0，2，9）三音進(jìn)行在輪廓上（見譜例7b）與201小節(jié)大提琴聲部的進(jìn)行相似，但通過(guò)節(jié)奏和其他因素削弱了這種關(guān)聯(lián)，實(shí)現(xiàn)了不變性的呼應(yīng)。

三、結(jié)語(yǔ)

任何關(guān)于“自由”十二音系統(tǒng)的創(chuàng)作都必須面對(duì)這樣一個(gè)問(wèn)題：這種所謂的“自由”是否會(huì)導(dǎo)致“不變性”的數(shù)量和范圍的維持、增加或減少，以及這種廣義化的表面“自由”在更深層意義上是否會(huì)減少而不是增加結(jié)構(gòu)性資源。同樣地，將十二音系統(tǒng)運(yùn)行于不變性結(jié)構(gòu)邏輯中的一個(gè)必要條件是，不變量是系統(tǒng)音高性質(zhì)的必要結(jié)果。十二音系統(tǒng)中的“不變性”技術(shù)就如同數(shù)學(xué)中的不變量，是在一系列變換或運(yùn)算下保持不變的屬性或值。它是系統(tǒng)的一個(gè)不變的特征，可以用來(lái)對(duì)系統(tǒng)的行為做出一般的陳述和預(yù)測(cè)。“不變性”的基本思想是不管十二音系統(tǒng)如何變化，它都具有恒定的屬性，通過(guò)識(shí)別和理解這些保持不變的特征，對(duì)整個(gè)十二音系統(tǒng)做出有效分析。

對(duì)于巴比特的超級(jí)序列矩陣而言，音高組織的“不變性”屬性來(lái)自矩陣音集間界限垂直分割而形成的復(fù)合音集。在這種大型復(fù)合矩陣結(jié)構(gòu)中，巴比特一直在追求某種不變性，既是技術(shù)層面，也是繼承著勛伯格最具有機(jī)性的發(fā)明——配套性的不變思維。十二音系統(tǒng)的音高資源不會(huì)也不可能被“耗盡”，其結(jié)構(gòu)手段的廣泛性、靈活性和精確性，從不遜色于任何過(guò)去或現(xiàn)在的作曲系統(tǒng)，因?yàn)樗牟蛔冃砸恢蔽魳?lè)創(chuàng)作者的思想。

作者簡(jiǎn)介：魏雨薇，博士，上海音樂(lè)學(xué)院教師。

[1]參見[美]約瑟夫·內(nèi)森·施特勞斯：《后調(diào)性理論導(dǎo)論》（第三版），齊研譯，人民音樂(lè)出版社，2014，第204頁(yè)。“Any musical quality or relationship preserved when the series transformed called an invariant. As we hear our way through a piece， our ear often led via chain of invariants.”

[2]Milton Babbitt， “Twelve-Tone Invariants as Compositional Determinants，” The Musical Quarterly 46/2 （1960）：246-259.

[3]指任意數(shù)量的連續(xù)集合元素，該屬性對(duì)任何元素選擇（非連續(xù)和連續(xù)）都同樣適用。

[4]第一個(gè)數(shù)字表示序列號(hào)，第二個(gè)數(shù)字表示音高。其中由于G為0，A音與E音則分別為1與7。

[5]集合分類表中共有50個(gè)六音集合，其中有6個(gè)六音集合可以在全部四種類型的變型后得到其配套集合：A（012345）；B（023457）；C（024579）；D（012678）；E（014589）；F（02468T）。

[6]可進(jìn)一步參見魏雨薇：《基于“配套思維”的音樂(lè)超級(jí)序列矩陣技術(shù)》，《音樂(lè)藝術(shù)》2023年第2期，第172～183+5頁(yè)。即〈0378e4〉可整理為〈048〉與〈37e〉，〈2619t5〉可整理為〈26t〉與〈159〉。

[7]可進(jìn)一步參見魏雨薇：《“限制即自由”——安德魯·米德〈米爾頓·巴比特音樂(lè)導(dǎo)論〉述評(píng)》，《人民音樂(lè)》2019年第12期，第78～81頁(yè)。

[8]分別是（0，0）與（1，3）；（2，7）與（3，8）；（4，e）與（5，4）；（6，2）與（7，6）；（8，1）與（9，9）；（10，t）與（11，5）。

[9]它們之間分別距離6個(gè)半音和5個(gè)半音。

[10]P6為〈69125t80734e〉。

[11]P6所剩（0，6）（3，2）（6，8）（7，0）；P0所剩（0，0）（3，8）（6，2）（7，6）。

[12]Milton Babbitt， “Set Structure as a Compositional Determinant，” Journal of Music Theory 5/1 （1961）：72-94.

[13]表格及示例中序列用“短橫線加數(shù)字”代替下標(biāo)表示，以做區(qū)分，下同。

[14]可以用數(shù)學(xué)中的組合算法得到，即從n集合中取出m個(gè)元素組合的可能性共為。

[15]P0、P1、Pe的前七音截?cái)喾謩e為（0378e42）（1489053）（e267t31）。

[16]同理，用公式可得（0145）包含4種三音集合——2個(gè)（014）與2個(gè)（015）集合。