聚焦新課標導向，建構作業設計新思路

【摘 要】本文主要依據《義務教育數學課程標準（2022年版）》的要求，依標扣本，整體定位作業目標；聯系生活，整體呈現作業內容；突出問題，整體優化作業設計三個方面來闡述單元作業設計的新思路。

【關鍵詞】新課標 作業設計 新思路

《義務教育數學課程標準（2022年版）》（以下簡稱《課程標準》）對教師提出更高的要求，也給教學實踐指明了方向。作業設計是教師日常工作的重要環節。教師承擔作業設計的任務，學生是完成作業的主體。教師依舊照本宣科，按傳統的模式給學生布置大量同質化的作業已不符合《課程標準》的要求。當下，教師應聚焦《課程標準》的新導向，圍繞課程教學目標，設計科學的學業評價體系，平衡知識理解與能力發展的權重，在尊重教材已有作業的基礎上，構建作業設計新思路。以下筆者以人教版四上“三位數乘兩位數”單元的作業設計為例加以闡述。

一、依標扣本，整體定位作業設計目標

《課程標準》是課程改革的指揮棒。《課程標準》的頒布給傳統教學模式帶來巨大的變革，大部分教師比較重視課堂教學，然而教師對如何依標扣本進行新型的數學作業設計不夠重視。傳統的作業設計，教師往往針對所學知識進行設計，這顯然是不全面的，作業設計應有明確的作業目標。因此，在制訂作業目標時，要正確把握數學核心素養和“四基”“四能”，抓住數學本質，樹立全新的教學觀念，根據學生的學習情況，整體定位作業目標。以“三位數乘兩位數”作業設計為例，從《課程標準》、教學目標、學生學情三個階段來整體定位本單元的作業目標。《課程標準》階段：（1）理解運算意義，解決實際問題；（2）弄清運算原理，掌握運算規則。教學目標階段：（1）掌握運算方法，理解運算原理；（2）找出數量關系并解決實際問題。學生學情階段：（1）部分學生的運算能力有待加強訓練；（2）算法掌握不牢，算理理解不透，解決問題能力有待提高。明確以上情況后再定位新的單元作業目標：（1）出示算式，正確率要求達到93%以上；（2）結合實情，理解算理；（3）制訂解決問題方案，讓學生能夠靈活解決問題。作業目標中的（1）和（2）是針對大部分學生“學”的要求，也就是對算法的掌握、算理的理解。教師要時刻關注學生的個體差異，讓學生達成符合自己的目標，讓學生數學素養有不同程度的提升。

二、聯系生活，整體呈現作業內容

作業的功能是落實核心素養的途徑。傳統教學主要以講授為主，設計的作業以基本技能為主要內容，一般要求學生課后完成。“雙減”政策的實施要求重新構建課堂教學結構，課堂教學多采用講練結合的形式，其中課堂作業的設計注重真實情境。為此，教師在作業設計時要聯系生活，整體呈現學生感興趣的作業內容，還要綜合考慮、整體安排、精心設計，根據作業設計目標及教材的重難點，圍繞《課程標準》和單元教學目標，使作業內容與教學內容相融合，與學生的學習基礎相適應，并重視讓學生從知識的獲得向能力素養提升的轉變。

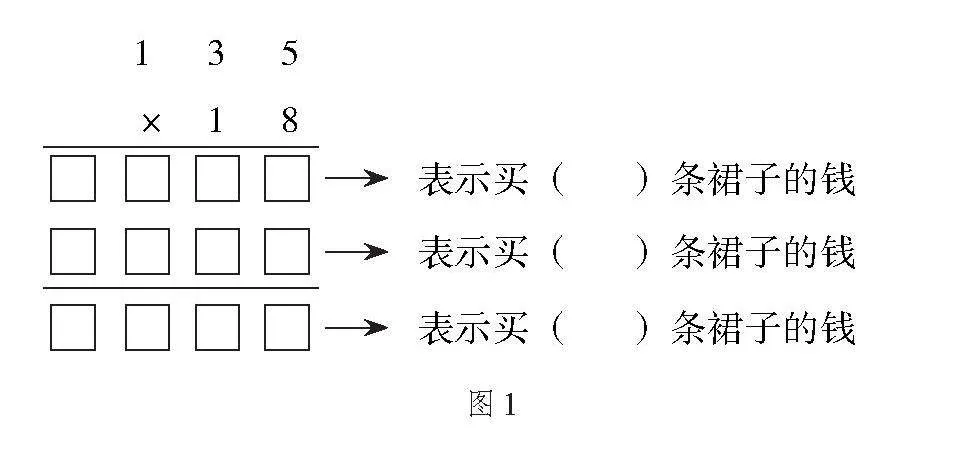
例如，教師出示問題：“六一兒童節”團體舞的表演需要學校購入18條舞裙，每條舞裙135元，共要多少元？要解決這個問題，首先引導學生正確列式135×18，再引導學生如何通過情境來理解算理，并掌握運算方法。教師讓學生觀察圖1，讓其算一算、說一說、填一填，再通過直觀演示和抽象推理將新知轉化為舊知，促使學生關注知識間的聯系，滲透轉化思想。通過圖1的剖析，學生懂得三位數乘兩位數應從個位算起，先算8條裙子的價錢，也就是8個135是多少；再算10條裙子的價錢，也就是10個135是多少；最后把8條裙子的價錢和10條裙子的價錢加起來，就是18條裙子一共要多少錢。這樣通過模擬生活中購買裙子的情境，學生理解了三位數乘兩位數乘法的算理，進而推出其算法，培養了他們的推理意識。

三、運用變式，引導學生深度學習

在數學教學中，作業是學生學習知識、形成技能的重要組成部分。因此，作業設計不能簡單地追求“量”，更要追求“質”。在作業設計時，教師可探求變式引發學生深度學習，即改變情境或問題的呈現方式，多選取創新情境，彰顯作業的趣味性、有序性、思維性，才能促進學生能力發展，注重知識與技能的理解與掌握。例如，教師鼓勵學生按要求自行列式計算：選用0～5六個數字設計作業。（1）寫出任意的三位數乘兩位數的算式并計算；（2）寫出中間有0的三位數乘兩位數的算式并計算；（3）寫出積末尾為0的算式并計算；（4）寫出因數末尾有0的算式并計算。通過這種特殊呈現方式，讓學生根據要求自行設計算式，促使學生對枯燥的計算有了興趣，并引導學生熟悉各類型三位數乘兩位數的運算方法，進而學會靈活選擇不同的運算策略。

四、突出問題，整體優化作業設計

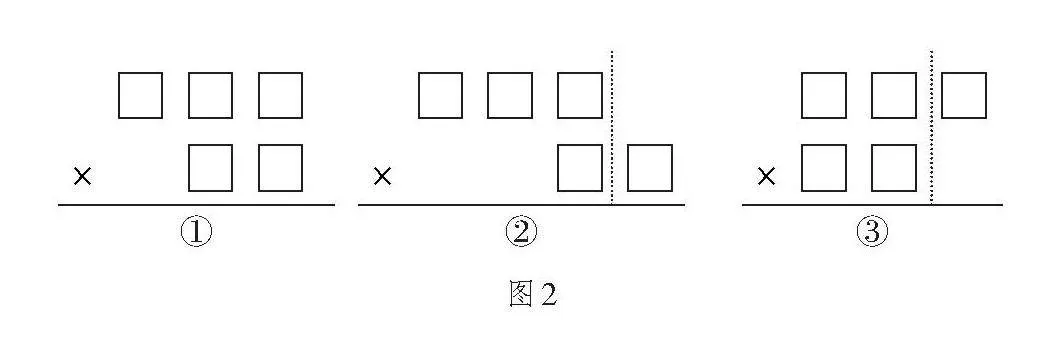
數學作業設計既要縱向溝通，也要橫向關聯，關注知識背后的思想和方法，挖掘作業中的思考性、靈活性。教師要把學生的思維激活，作業設計要從整體和部分兩個方面切入，以綜合性解決問題為主要內容，可以通過設置“問題串”的方式逐步剖析知識點。同時，打破思維定勢，圍繞核心問題，在學生好奇處、疑惑處、難點處設計作業，例如，設計一道突出因數末尾沒有“0”和末尾有“0”為主要內容的綜合性題目：根據□□□×□□算式。（1）寫出不同類型豎式模型；（2）在□里填上數字并計算；（3）說一說不同類型豎式模型中你的發現；（4）寫一個兩個因數都是三位數的算式，并試著計算；（5）請你思考兩個因數都是三位數的乘法算法與三位數乘兩位數算法有什么異同點。學生練習中反饋可能有3種不同類型的豎式模型，如圖2所示。

在上圖算式中，豎式模型①是最常規的三位數乘兩位數的形式，但這里有兩種類型，一種是三位數、兩位數個位都不是0，比如351×32。另一種也有可能三位數、兩位數個位都是0，那在三位數、兩位數個位□前面畫條虛線就明白兩個因數的個位都是0，這樣就與兩個因數的個位都不是0的模式區別開了，比如350×20。豎式模型②，在突出□前面畫條虛線更清楚看出兩位數個位是0，比如258×30。豎式模型③中突出的□是0，就是三位數的個位是0，也在突出□前面畫條虛線，比如830×26。

本題的設計意圖是讓學生打消乘法豎式數位對齊的思維定勢，明白在其中一個因數末尾有0時，豎式計算的數位應把末位的0往后突出，計算更簡便。當學生完成這道習題后，深刻理解數學知識是相互聯系的整體，并參透三位數乘兩位數與兩個因數都是三位數的豎式計算的聯系與區別，進而深刻理解算理的一致性，解除學生心中的疑慮，形成算法結構化，建立整數乘法的運算模型。

總之，小學數學作業設計要符合《課程標準》的要求，根據學生的年齡特征和實際情況，做到設計的數學作業內容新穎、形式多樣。同時，要樹立新的作業設計理念，尋找數學生活原型，把數學學習與生活實際聯系起來，增強作業的實踐性，使每一個學生愛數學，喜歡做數學作業，不斷提升其數學綜合素養。

（作者單位：福建省永泰縣東門小學 本專輯責任編輯：莊嚴 宋曉穎）

“雙減”背景下，作業設計越來越受到教師們的重視。根據學生的實際情況設計精準分層作業，滿足學生的個性化需求；設計能力型綜合實踐性作業，讓學生能在生活中靈活運用所學知識；基于認知心理學來優化習題設計，充分發揮習題的育人功能。本專輯的這幾篇文章在作業的設計上都有所創新，可供參考。