基于ARIMA-PSO-LSTM 的太陽能預測

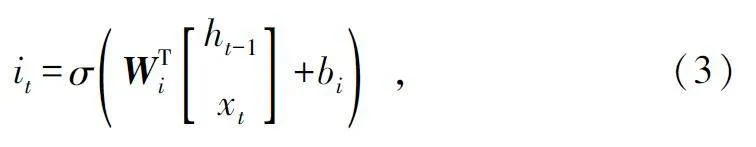
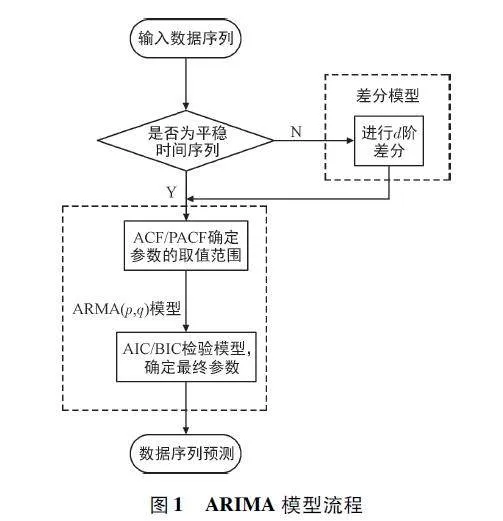
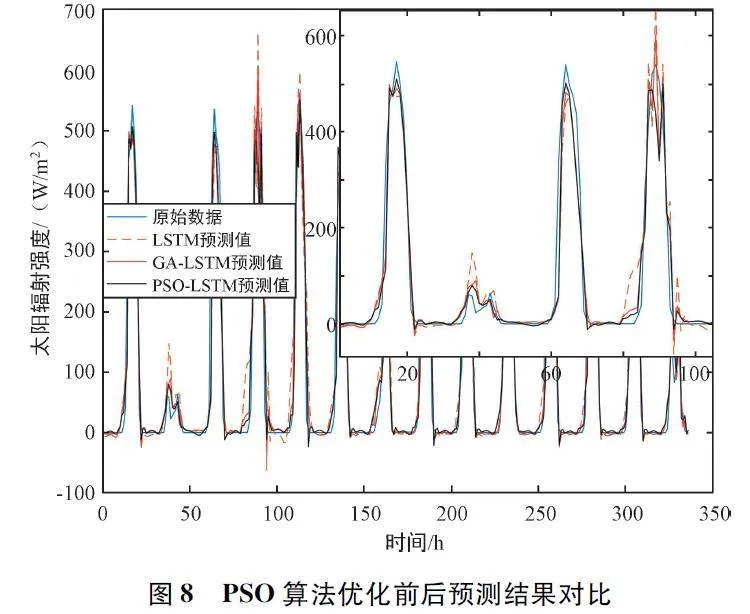
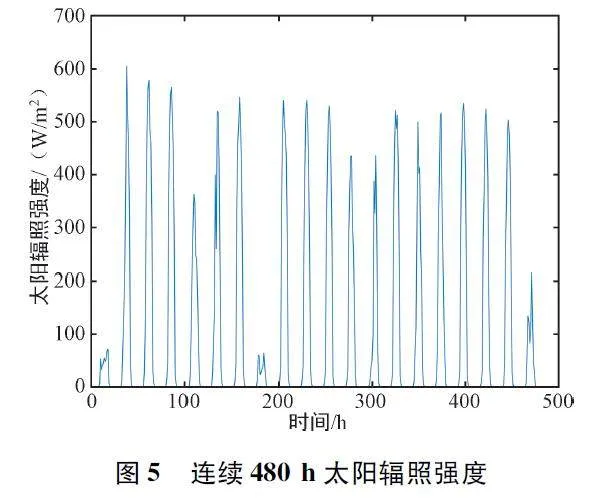
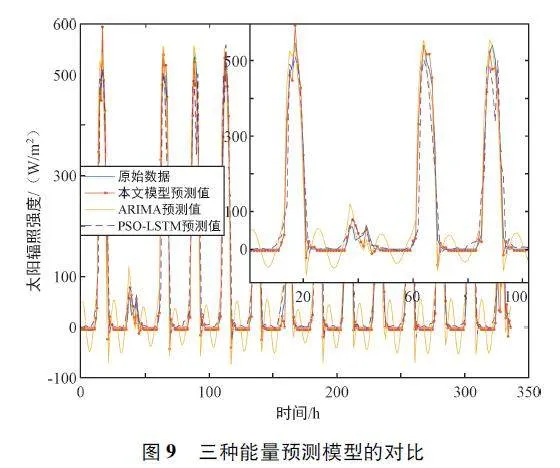
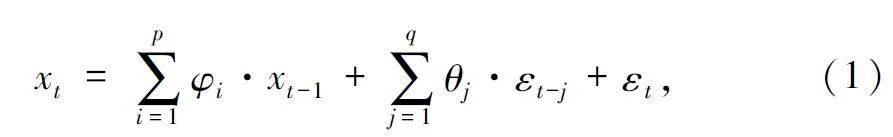
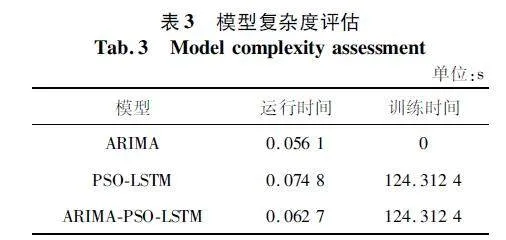
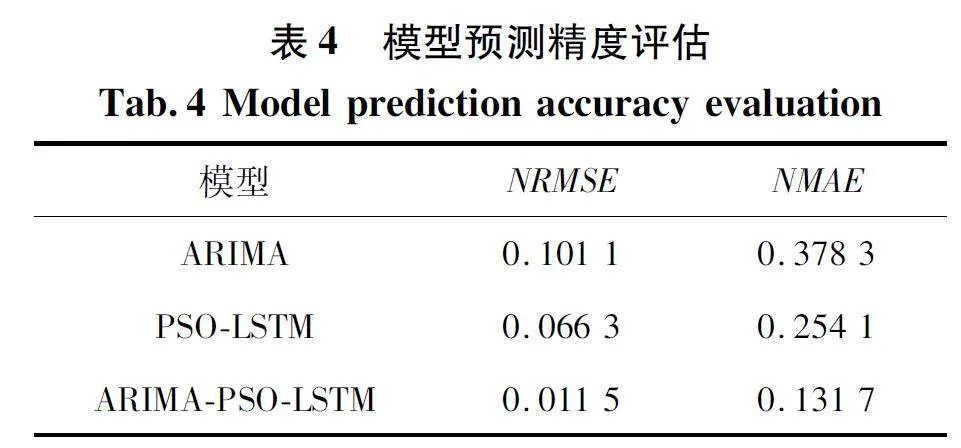
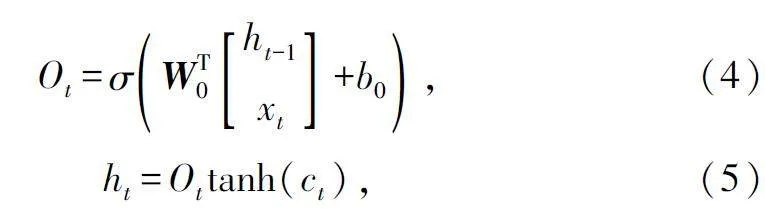
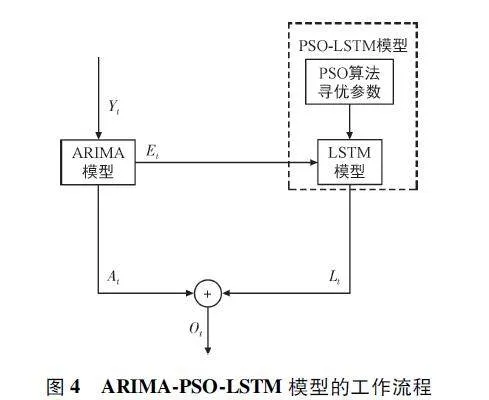
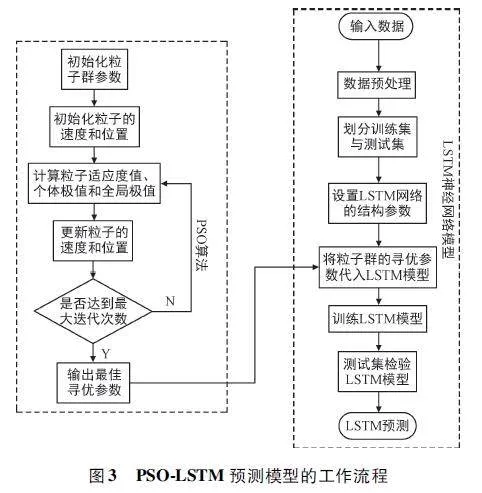
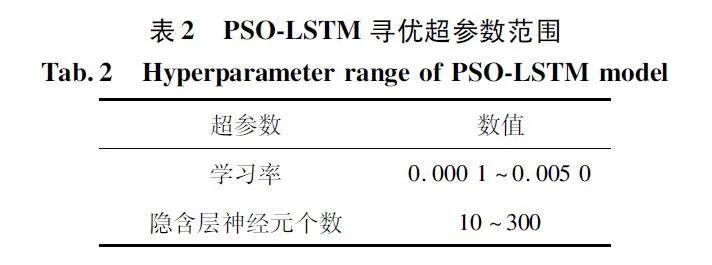
摘 要：太陽能是新興的可再生能源之一，可將其轉化為電能以供無線傳感器網絡（Ｗｉｒｅｌｅｓｓ Ｓｅｎｓｏｒ Ｎｅｔｗｏｒｋｓ，ＷＳＮ）使用，對太陽能進行預測可以有效地利用能量，從而達到節省能源、維持網絡持續穩定運行的目的。提出了一種新的組合預測模型來預測太陽能輻照強度，其中改進的粒子群優化（Ｐａｒｔｉｃｌｅ Ｓｗａｒｍ Ｏｐｔｉｍｉｚａｔｉｏｎ，ＰＳＯ）算法被引入尋找長短期記憶（Ｌｏｎｇ Ｓｈｏｒｔ Ｔｅｒｍ Ｍｅｍｏｒｙ，ＬＳＴＭ）神經網絡模型的最優參數。選取自回歸差分移動平均（Ａｕｔｏ-Ｒｅｇｒｅｓｓｉｖｅ Ｉｎ-ｔｅｇｒａｔｅｄ Ｍｏｖｉｎｇ Ａｖｅｒａｇｅ，ＡＲＩＭＡ）模型來預測太陽輻照數據中的線性分量；采用ＰＳＯ 算法來優化ＬＳＴＭ 神經網絡模型的超參數，有助于提高模型預測的精度和魯棒性；采用優化的ＬＳＴＭ 神經網絡模型來預測數據中的非線性分量；最后將兩個模型的預測結果進行疊加。實驗結果表明，新的組合模型比ＡＲＩＭＡ、ＬＳＴＭ 等模型，具有更高的預測精度。

關鍵詞：自回歸差分移動平均模型；長短期記憶神經網絡模型；粒子群優化算法；能量預測算法

中圖分類號：ＴＰ９２９ 文獻標志碼：Ａ 開放科學（資源服務）標識碼（ＯＳＩＤ）：

文章編號：１００３－３１１４（２０２４）０４－０７７１－０８

０ 引言

隨著無線傳感器網絡（Ｗｉｒｅｌｅｓｓ ＳｅｎｓｏｒＮｅｔｗｏｒｋｓ，ＷＳＮ）的發展，各種各樣的相關應用接踵而至［１－２］。在ＷＳＮ 中，環境能量是維持網絡運行的動力之一，采集的環境能量不穩定、不平衡，可能導致ＷＳＮ 運行不穩定。為解決上述問題，對環境能量進行適當的預測具有至關重要的意義。能量預測方法可以準確預測出未來所需采集的能量大小，有助于網絡合理規劃能量分配，使ＷＳＮ 節點能夠持續穩定運行，并且可以節省能源［３－７］。

為避免ＷＳＮ 節點因為能量不足而導致運行停止，延長ＷＳＮ 壽命，國內外學者對能量預測展開了一系列研究和探索［８－１４］。……