基于生成對抗網絡的鋰電池壽命預測

摘要：鋰電池廣泛應用于多個領域，但其性能隨時間退化，最終導致失效。為了解決GAN網絡在時間序列預測中的模式崩塌問題，本文提出了一種基于WGAN的鋰電池剩余使用壽命預測方法，該模型以GRU作為生成器和以CNN作為判別器，并在原有的損失函數基礎上引入L2范數以提高模型的收斂性，最后通過對抗訓練提高預測精度。使用CALCE鋰電池數據集驗證，WGAN模型在MAE、RMSE和R2評價指標上均優于其他模型，顯示出高預測精度和良好泛化性。不同訓練集占比下WGAN模型仍保持高預測性能，證明其廣泛的適用性。

關鍵詞：鋰電池；生成對抗網絡；WGAN；門控循環單元網絡；卷積神經網絡

中圖分類號：TM912 文獻標識碼：A

文章編號：1009-3044（2024）22-0019-06

開放科學（資源服務）標識碼（OSID）

0 引言

鋰電池的性能隨時間推移，其性能會退化，導致最終失效。在電池剩余使用壽命（Remaining Useful Life，RUL）預測研究中通常將電池容量電池健康狀態的直觀指標，通常當其降至70%～80%時，認為電池壽命結束[1]。

目前的鋰電池剩余壽命預測方法主要分為基于模型的RUL預測方法和基于數據驅動的RUL預測方法[2]，基于模型的方法依賴復雜電池模型，易受噪聲干擾，適應性差，且需理解電池內部的物理化學反應[3]。數據驅動方法則通過分析電池容量、電流、電壓等數據，提取健康特征，預測RUL，且不受電池內部模型限制[4]。李練兵等[5]提出基于差分電壓和Elman網絡的方法，分析差分電壓和充放電曲線，提取電池容量退化特征，構建以電池容量為輸出的網絡，提升鋰電池RUL預測精度。Chen等[6]提出基于Transformer的鋰電RUL預測法，用自動去噪編碼器（Denoising Auto Encoder，DAE）處理電池容量再生，后用Transformer預測RUL，表現優于傳統算法。吳瓊等[7]提出用遺傳算法優化BP網絡估算鋰電剩余容量，主成分分析降維健康因子，優化權值，預測RUL。黃凱等[8]提出CEEMDAN-LSTM預測法，先分解降噪容量序列，再相關性分析選殘差，用LSTM建模預測鋰電RUL，精度高。

基于以上分析，提出一種基于生成對抗網絡的鋰電池RUL預測方法。該方法構建了生成器為GRU，判別器為CNN的Wasserstein生成對抗網絡（Wasserstein GAN，WGAN）鋰電池剩余使用壽命預測模型。

1 相關理論

1.1 門控循環單元網絡

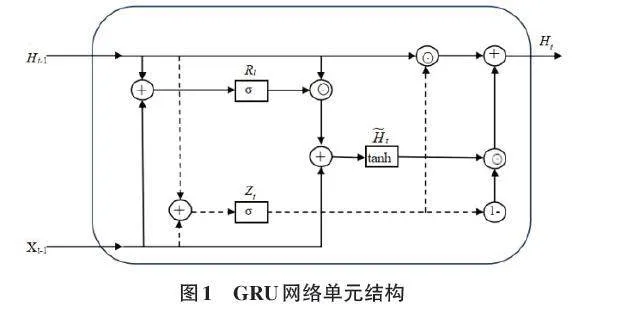
門控循環單元網絡（Gated Recurrent Unit Network， GRU）是2014年Cho和Chung提出的RNN門控變體[9]，比LSTM簡單，參數少，計算高效，時序任務表現好。其結構如圖1所示。

重置門Rt和更新門Zt的計算公式如下：

[ [Rt=σ（WrxXt+WrhHt-1+br）] （1） [Zt=σ（WzxXt+WzhHt-1+bz）] （2） ]

其中σ（·）為Sigmoid激活函數，Wrx，Wzx和Wrh，Wzh為各門控結構對應輸入值Xt和隱藏狀態Ht-1的權重參數，br，bz為各門控結構的偏置參數。

候選隱藏狀態[Ht]用于計算隱藏狀態Ht，具體計算公式如下：

[ [Ht=tanh（WhxXt+Whh（Rt⊙Ht-1）+bh）] （3） ]

式中：tanh（·）為雙曲正切5pOWM7hGOWgFR2uBixkjyDoUNFnxopVLKeWOg5na0sE=激活函數，Whx和Whh為候選隱藏狀態的權重參數，bh候選隱藏狀態的偏置參數，[⊙]表示哈達瑪積（按元素乘法）。重置門Rt決定了[Ht]的更新是否受前一時刻隱藏狀態Ht-1的影響。

最后，由更新門Zt和候選隱藏狀態[Ht]計算隱藏狀態Ht供輸出層使用，具體計算公式如下：

[ [Ht=Zt⊙Ht-1+（1-Zt）⊙Ht] （4） ]

其中，更新門Zt負責調節保留自前一時刻隱藏狀態Ht-1的歷史信息量，以及從候選隱藏狀態[Ht]接收新信息的比例，進而融合這些信息以生成當前時刻的隱藏狀態Ht。

1.2 生成對抗網絡

生成對抗網絡（Generative Adversarial Network，GAN）[10]由生成器和判別器組成，用于圖像生成，學習真實數據分布，判別數據真假。GAN廣泛應用于圖像、視頻、時間序列預測等領域。

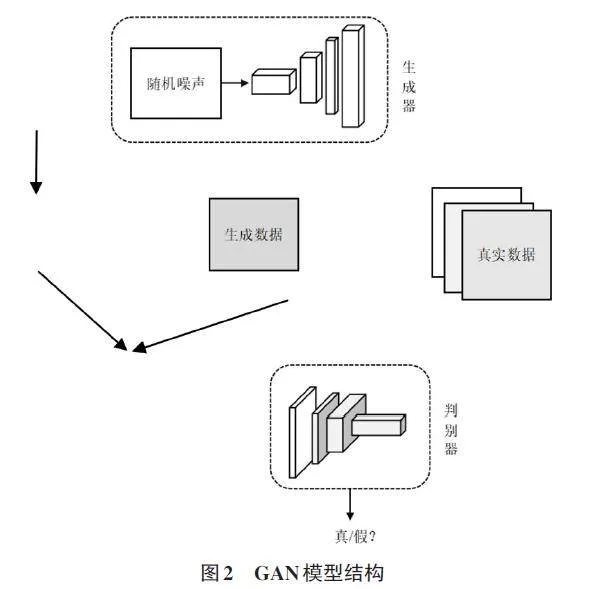
在生成對抗網絡的訓練過程中，生成器與判別器通過相互競爭達到一種平衡，類似于博弈論中的“納什均衡”，判別器難以區分生成器產出的數據與真實數據。GAN是一個靈活的生成模型框架，允許內部結構的多樣性，可以選擇CNN、RNN、LSTM等不同的網絡結構來適應不同的應用需求。GAN模型結構如圖2所示。

模型理想狀態：生成器掌握數據分布，生成逼真數據；判別器在無法辨識數據真偽時，其輸出概率為50%。GAN的目標函數如下所示：

[minGmaxDY（D，G）=Ex～Pdata（x）[log（D（x））]+Ex～PG（z）[log（1-D（G（z）））]] （7）

式中，x為輸入數據，D（x）表示判別器判斷該輸入數據為真的概率，G（z）表示生成器根據隨機噪聲z生成的虛假數據。Pdata（x）表示真實數據的分布，PG（z）是生成器學習到的虛假數據的分布。E則是計算其期望。公式（7）分兩部分，先k次優化判別器D，再優化1次生成器G，交替訓練。

1.3 Wasserstein生成對抗網絡

Wasserstein生成對抗網絡（Wasserstein GAN，WGAN） [11]是對經典GAN模型的一個改進。其增強了模型的穩定性，解決了GAN模式崩塌的問題。WGAN與經典GAN模型相比，做出了以下4處優化：

（1）判別器輸出層去除sigmoid，將任務從二分類轉為回歸；

（2）損失計算中去除對數，增大損失值以助訓練；

（3） 訓練判別器時參數截斷，限制參數范圍以緩解梯度消失；

（4）棄用動量優化，推薦RMSProp或SGD，以提升模型收斂速度。

WGAN中參數截斷應對判別器梯度的Lipschitz限制，確保不超過閾值K。為克服截斷帶來的問題，引入梯度懲罰機制，以替代固定閾值，既滿足限制也保持了判別器性能。此時判別器的損失函數如式（8）所示：

[LossD=-Ex～Pr[D（x）]+Ex～Pg[D（x）]+λEx～px?xD（x）p-12] （8）

其中，Pr代表真實數據的概率分布，而Pg代表生成器所模擬的數據分布。兩者之間的差異構成了分布區域[px]，E用來表示這個區域的期望值。通過在xr和xg之間進行插值[x]，引入了介于0到1之間的隨機變量ε，計算公式如下：

[x=εxr+（1-ε）xg，xr～Pr，xg～Pg，ε～Uniform[0，1]] （9）

2 WGAN模型結構

2.1 生成器結構

本文采用GRU作為生成器的核心網絡結構，利用其穩定性優勢，并通過全連接層來產生所需的數據輸出。針對鋰電池剩余使用壽命預測，本文采用改進的WGAN損失函數，由對抗損失和預測損失兩部分組成。對抗損失基于WGAN原始損失，促使生成器的數據分布與原始數據一致；預測損失衡量生成數據與真實數據的誤差。在優化問題中，L2范數常作為正則化項，以防止模型過擬合，因此本文使用L2范數作為預測誤差的度量，有助于生成器更準確地捕捉時間序列的特征和結構，提升生成器生成數據的質量。生成器的損失函數如公式（10）所示。

[ [lossG=-D（y）+λy-y2] （10） ]

在上式中，λ為權重，控制對抗損失和預測損失比例，優化訓練。[y]為生成器預測值，y為真實數據，[D（y）]是判別器結果。最小化lossG同時最大化判別器對[y]的判別，減小預測誤差，實現收斂。

2.2 判別器結構

本文的WGAN判別器融合了一維卷積神經網絡和全連接層，發揮了CNN在處理分類任務時的長處。判別器由三層一維卷積層、最大池化層和兩層全連接層構成。為增強訓練效能，卷積層中使用了帶泄露的線性整流單元（Leaky ReLU）激活函數，而輸出層則沿用了WGAN模型的線性激活函數。該線性激活函數產生的分數，量化了生成數據與真實數據的相似性。損失函數則基于Wasserstein距離，用于指導判別器的訓練，公式如（11）所示。

[ [lossD=-D（y）+D（y）] （11） ]

上式中，y表示實際的鋰電池容量數據，而[y]表示生成器生成的虛假容量數據。

訓練過程的目標是最小化公式（11）定義的損失函數lossD，這涉及在提升判別器對真實數據D（y）的判別能力的同時，降低其對生成數據[D（y）]的判別效果。

3 實驗結果與分析

3.1 數據集介紹

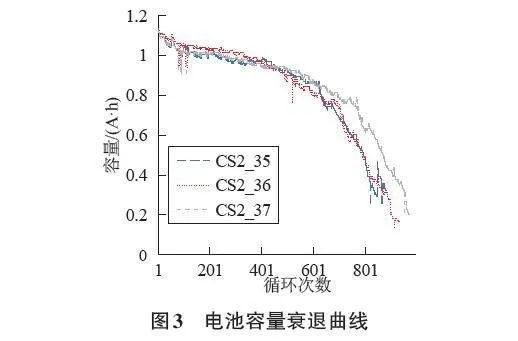
模型的輸入數據來自馬里蘭大學先進生命周期工程研究中心（CALCE） 的鋰電池數據集中的CS2_35、CS2_36、CS2_37三個電池的充放電實驗數據[12]。如圖3所示為鋰電池的容量衰退曲線。

3.2 模型訓練

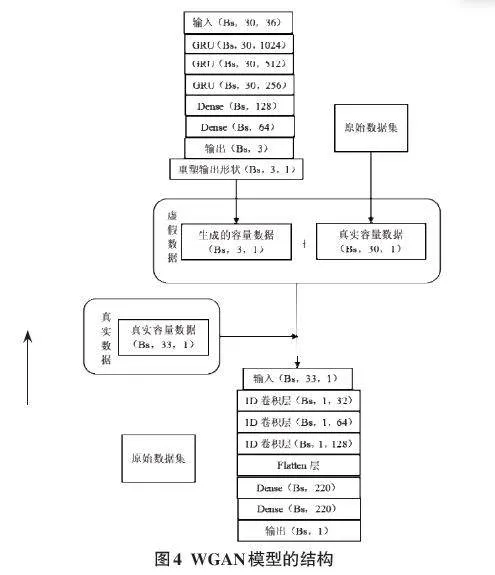
本文將從馬里蘭大學鋰電池數據集中所提取的4個特征作為輸入，通過WGAN模型進行預測鋰電池容量數據。該模型的結構圖如圖4所示（注：圖中的Bs為批量大小）。從圖中可以看出，本文所提出的WGAN模型的生成器有三個GRU層，分別有1 024，512，256個神經元；兩個Dense層，分別有128和64個神經元。判別器有三個1D卷積層，分別有32，64，128個神經元；一個Flatten層。

WGAN的訓練過程遵循生成器和判別器交替更新的迭代方法，具體步驟如下：

1） 模型輸入階段：將訓練數據送入模型。

2） 判別器D更新：固定生成器G的參數，將由G生成的預測數據與實際數據混合后送入判別器D。隨后，利用Adam優化算法對D的權重進行調整。

3） 生成器G更新：保持判別器D參數不變，將訓練數據輸入G得到預測數據，隨后將這些數據與真實數據一起輸入D，以此來評估G生成的數據。

4） 迭代優化：重復步驟1至3，G和D的網絡參數持續優化，損失函數值逐漸減小，預測結果逐步逼近真實值。

3.3 模型評價指標

模型的預測結果，采用平均絕對誤差（Mean Absolute Error，MAE） 、均方根誤差（Root Mean Square Error，RMSE） 和決定系數（R2 score，R2） 這三個指標進行評估。其計算公式見式（12）～（14）：

[ [RMSE=1nt=1nxt-xt2] （12） [MAE=1nt=1nxt-xt] （13） [R2=1-[t=1nxt-xt2][t=1nxt-xt2]] （14） ]

3.4 實驗結果與分析

為了驗證本文選擇GRU作為生成器比LSTM作為生成器的優越性，以CS2_35電池為例分析LSTM和GRU的預測能力。

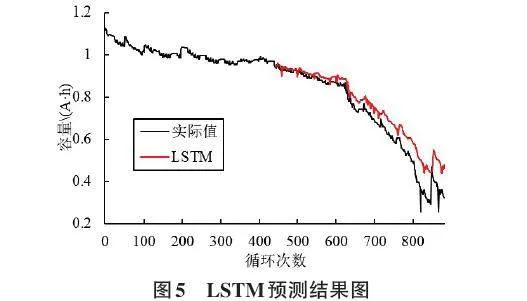
在LSTM模型中，使用了一層LSTM，模型的優化器是Adam算法，學習率為0.001。批處理大小是64，然后在訓練集上迭代了50次。如圖5所示為LSTM在CS2_35上的預測結果圖。

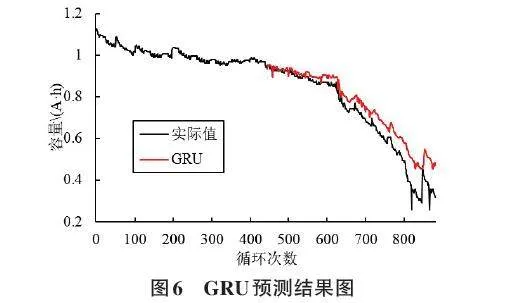
在構建GRU模型時，使用了兩層GRU，它的優化器為Adam算法，學習率為0.000 1，批量大小為32，然后在訓練集上迭代了50次。如圖6所示為GRU在CS2_35上的預測結果圖。

從圖5和圖6可以看出LSTM與GRU的預測結果沒有明顯的差距，LSTM的MAE為0.054 2，而GRU的MAE為0.057 3，兩者之間的差距很小。然而LSTM模型的訓練時間為8.561 5 s，GRU模型的訓練時間為6.812 s。這說明兩者在預測精度方面沒有明顯的區別，但是在訓練時間上有不小的差距，為了減少時間開銷，本文的WGAN模型的生成器選擇了GRU。

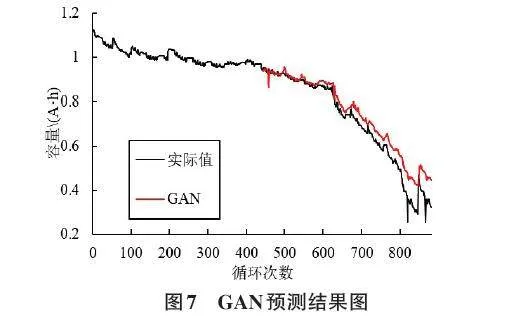
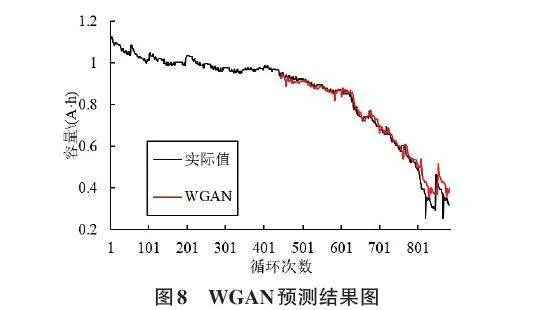
構建GAN和WGAN模型的結構時，模型的生成器是GRU，判別器是CNN，優化器是學習率為0.000 16的Adam算法。批處理的大小是128，在訓練集上迭代了300次。如圖7和圖8所示，分別為GAN和WGAN在CS2_35上的預測結果圖。

從圖7和圖8可以看出，WGAN和GAN都具有不錯的預測精度，但WGAN的預測效果更好一些。如圖9所示，上方藍線為判別器的損失曲線，下方橙色線為生成器的損失曲線。在500次迭代后，可以明顯地看出，GAN的判別器的損失曲線一直高于生成器的損失曲線，在100次迭代后趨于穩定，而WGAN的判別器的損失曲線隨著迭代次數的增加，逐漸減小，直到趨近于0。與GAN模型相比，WGAN的判別器的學習能力更強，預測效果也更好。

在訓練集和測試集各占數據集的50%情況下，四種模型在CS2_35、CS2_36、CS2_37三個電池上的RUL預測結果的評價指標如表1所示。

通過表1可觀察到WGAN模型在對CS2_35、CS2_36和CS2_37電池的RUL進行預測時，其表現優于其他三種模型。WGAN模型的MAE和RMSE都顯著低于GRU、LSTM和傳統GAN模型，表明WGAN模型在預測鋰電池的RUL時，能夠提供更為精確的估計，誤差更小，擬合度更高。R2值越高，表明模型的預測值與實際值之間的相關性越強，預測的可信度和準確性越高。WGAN模型的R2值在所有模型中是最高的，這意味著其預測結果與實際值更為貼近。

通過圖10可以觀察到WGAN模型的預測曲線緊密貼合實際的電池容量退化曲線，顯示出其在捕捉電池容量波動趨勢方面的高準確度。隨著電池循環次數的增加，WGAN模型依然能夠維持較高的預測精度，而GRU、LSTM和傳統GAN模型的預測曲線則逐漸偏離實際曲線，顯示出它們的擬合效果隨著時間的推移而下降。

進行鋰電池RUL預測時，WGAN模型在不同規模的訓練集上的表現是評估其泛化能力和魯棒性的關鍵。通過將數據集分別劃分為40%、50%和60%作為訓練集，能夠深入理解WGAN模型在不同訓練數據條件下的預測能力。不同訓練集下的預測結果如圖11所示。

由圖11可知，隨著訓練集規模的增加，WGAN模型的預測精度逐漸提高。在40%訓練集中，WGAN模型能夠捕捉到電池容量的大致退化趨勢。當訓練集為50%時，WGAN模型的預測曲線與實際曲線的吻合度提高，具有更好的擬合效果。當訓練集為60%時，WGAN模型的預測精度更高，預測曲線幾乎與實際曲線重合，這表明WGAN模型在較大訓練集的支持下能夠實現高度精確的RUL預測。

從表2中可以看出，隨著訓練集的增加，MAE和RMSE逐漸減小，而R2值逐漸增大，這與圖11的觀察結果一致。較小的訓練集可能導致模型欠擬合，而較大的訓練集則有助于模型更好地學習數據中的模式，從而提高預測的準確性和可靠性。

因此，WGAN模型在不同訓練集規模下的RUL預測測試結果表明，該模型具有良好的泛化能力和適應性。

4 結論

為了對鋰電池RUL準確預測，本文提出了基于生成對抗網絡的鋰電池剩余使用壽命預測模型。該模型首先使用作為生成器的GRU進行預測，再使用作為判別器的CNN進行判別，根據判別器的反饋，更新生成器的訓練參數，以生成質量更高的數據來訓練判別器的識別能力；這種對抗訓練的過程不斷迭代，使得模型持續優化，最終得到鋰電池RUL的預測結果。實驗結果表明WGAN具有更低的預測誤差，WGAN模型在不同數據集上的RUL預測都有較好的準確性，證明該模型的鋰電池RUL預測精度更高，泛化性更強。

參考文獻：

[1] 梁海峰，袁芃，高亞靜.基于CNN-Bi-LSTM網絡的鋰離子電池剩余使用壽命預測[J].電力自動化設備，2021，41（10）：213-219.

[2] 李超然，肖飛，樊亞翔，等.基于卷積神經網絡的鋰離子電池SOH估算[J].電工技術學報，2020，35（19）：4106-4119.

[3] 鄭雪瑩，鄧曉剛，曹玉蘋.基于能量加權高斯過程回歸的鋰離子電池健康狀態預測[J].電子測量與儀器學報，2020，34（6）：63-69.

[4] 裴洪，胡昌華，司小勝，等.基于機器學習的設備剩余壽命預測方法綜述[J].機械工程學報，2019，55（8）：1-13.

[5] 李練兵，李思佳，李潔，等.基于差分電壓和Elman神經網絡的鋰離子電池RUL預測方法[J].儲能科學與技術，2021，10（6）：2373-2384.

[6] CHEN D Q，HONG W C，ZHOU X Z.Transformer network for remaining useful life prediction of lithium-ion batteries[J].IEEE Access，1975，10：19621-19628.

[7] 吳瓊，徐銳良，楊晴霞，等.基于PCA和GA-BP神經網絡的鋰電池容量估算方法[J].電子測量技術，2022，45（6）：66-71.

[8] 黃凱，丁恒，郭永芳，等.基于數據預處理和長短期記憶神經網絡的鋰離子電池壽命預測[J].電工技術學報，2022，37（15）：3753-3766.

[9] 邱錫鵬.神經網絡與深度學習[J].中文信息學報， 2020（7）：1.

[10] LINTING M，VAN DER KOOIJ A.Nonlinear principal components analysis with CATPCA：a tutorial[J].Journal of Personality Assessment，2012，94（1）：12-25.

[11] ARJOVSKY M， CHINTALA S， BOTTOU L. Wasserstein generative adversarial networks[C]//International conference on machine learning. PMLR， 2017： 214-223.

[12] 史永勝，施夢琢，丁恩松，等.基于CEEMDAN-LSTM組合的鋰離子電池壽命預測方法[J].工程科學學報，2021，43（7）：985-994.

【通聯編輯：李雅琪】