動量觀點在多過程問題中的應用

【摘要】本文以一道經典的多次碰撞問題為例，探討動量觀點在高中物理教學中的應用價值.通過分析物體在碰撞過程中的速度變化和動量傳遞，展示動量定理和動量守恒定律在解決實際問題中的重要作用.通過解決多次碰撞問題，學生能夠培養分析和解決復雜物理問題的能力，提高邏輯思維能力.

【關鍵詞】高中物理；碰撞問題；動量定理

1 引言

動量定理和動量守恒定律是高中物理中的重要概念，多次碰撞問題是一種復雜的物理現象，涉及多個物體的相互作用和動量的傳遞.通過應用動量定理和動量守恒定律，學生可以準確地計算物體在碰撞過程中的速度變化.通過解決多次碰撞問題，學生可以培養分析和解決復雜物理問題的能力，提高邏輯思維和數學建模的能力.同時，他們也能夠深入理解動量定理的物理意義和應用范圍，增強對物理學的興趣和認識.因此，本文通過一道經典的多次碰撞問題，探討動量定理和動量守恒定律在高中物理教學中的應用價值，以期提高學生對物理學的理解和興趣，培養他們的科學思維和問題解決能力.

2 試題呈現

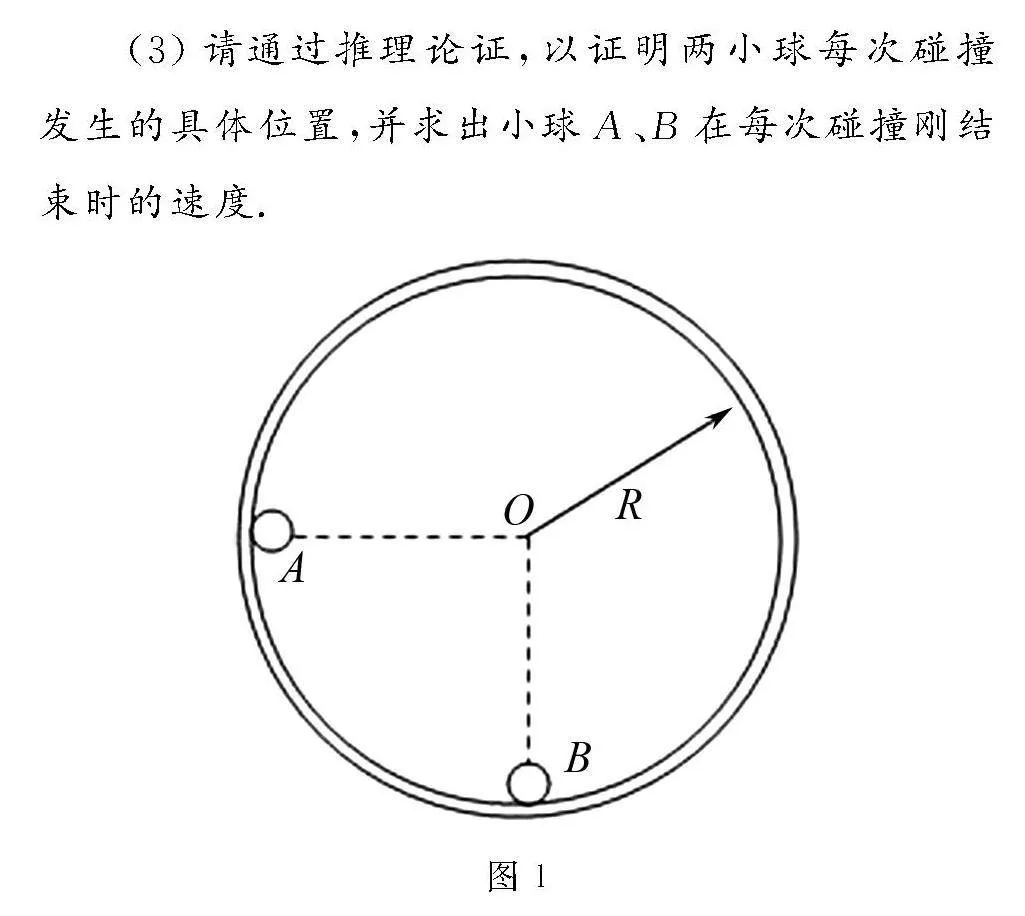
例1 如圖1所示，半徑為R的光滑圓形軌道固定在豎直面內.小球A、B的質量分別為m、3m.A球從左邊與圓心等高處由靜止開始沿軌道下滑，與靜止于軌道最低點的B球相撞，碰撞中無機械能損失.重力加速度為g.

（1）求第一次與小球B碰撞前的瞬間，小球A的速度大小；

（2）計算在第一次碰撞的過程中，小球A對小球B的沖量大小；

（3）請通過推理論證，以證明兩小球每次碰撞發生的具體位置，并求出小球A、B在每次碰撞剛結束時的速度.

圖1

3 思路分析

首先，在小球A下滑的過程中，由于忽略空氣阻力和摩擦力，在無外力作用的情況下，系統的機械能保持不變.利用這一條件，可以根據機械能守恒原理來計算碰撞發生前某一小球的運動速度.隨后，當兩個小球相互作用發生碰撞，系統內的總動量和總機械能都保持不變.通過運用動量守恒定律和機械能守恒定律，可以推導出碰撞后兩個小球的速度.

接著，利用動量定理，可以進一步計算出小球A對小球B的沖量大小.

最后，兩球碰撞后的運動過程中，機械能仍然守恒.通過應用機械能守恒定律，可以分析出再次碰撞點的位置.在兩球再次碰撞時，動量和機械能同樣守恒.通過再次應用動量守恒定律和機械能守恒定律，可以求解出碰撞后的速度.

4 解法探究

（1）A球下滑過程機械能守恒，由機械能守恒定律得：mgR=12mv2，

解得v=2gR.

（2）兩球碰撞過程系統動量守恒，以向右為正方向，由動量守恒定律得：mv=mv1+3mv2，

碰撞過程機械能守恒，由機械能守恒定律得：

12mv2=12mv21+12×3mv22，

解得：v1=－122gR，v2=122gR，

對B球，由動量定理得：I=3mv2－0，

解得A對B的沖量大小I=3m2gR2.

（3）在第一次碰撞之后，兩個小球的速度等大反向，隨后它們各自沿著原軌道進行圓周運動.由于軌道光滑，小球的機械能保持不變.因此，兩個小球將同時到達最高點，并且也將同時返回到最低點.當它們回到最低點時，其速度大小將會恢復到碰撞前的水平122gR，在最低點發生第二次碰撞；碰撞過程系統動量守恒，以向右為正方向，由動量守恒定律得：－mv1－3mv2=mv′1+3mv′2，

由機械能守恒定律得：

12mv21+12×3mv22=12mv′21+12×3mv′22，

解得v′1=－2gR，v′2=0，

由此可知，第二次碰撞后，B球停在最低點，A球碰撞后反彈返回到最初位置；

第三次碰撞與第一次碰撞相同，第四次碰撞與第二次碰撞相同，以此類推，每次碰撞都發生在最低點.

由此可知，當碰撞次數為奇數次時，

v1=－122gR，v2=122gR；

當碰撞次數為偶數次時，

v′1=－2gR，v′2=0.

5 結語

在解決這類多次碰撞問題時，正確理解和應用動量守恒定律是解題的核心.首先，需要對小球的運動過程有一個清晰的分析，這是解題的前提和關鍵.在這個特定的物理問題中，小球沿著軌道滑動時，其機械能保持不變，可利用機械能守恒定律來確定碰撞發生前小球的速度.隨后，當兩個小球相撞，整個系統的動量和機械能都保持不變，可以應用動量守恒定律和機械能守恒定律來計算碰撞后兩個小球的速度.進一步地，由于碰撞后兩球的速度等大反向，可以推斷它們將分別沿著各自的軌道進行圓周運動.由于軌道的平滑特性，兩球的機械能繼續守恒，導致它們在軌道上上升到任何相同高度時的速度都相同.最后，根據這些分析，可以得出兩球同時運動到最高點，再同時回到最低點，回到最低點時速度大小都恢復到碰撞前的水平.通過這樣的解題過程，學生不僅能夠鞏固對動量守恒定律的理解，還能夠培養分析和解決復雜物理問題的能力.因此，動量定理和動量守恒定律在高中物理教學中的應用價值不可忽視.通過解決經典的多次碰撞問題，學生能夠深入理解動量定理和動量守恒定律的物理意義和應用范圍，培養分析和解決復雜物理問題的能力.

參考文獻：

［1］李佳.高中物理課堂提問教學研究——以動量定理教學片段為例［J］.數理化解題研究，2023（15）：80-82.

［2］張保雷，田慧穎.指向高階思維培養的高中物理備考作業設計——以動量定理求解流體問題為例［J］.教學考試，2023（22）：78-80.

［3］許誥.高中物理教學策略分析——以動量定理的教學為例［J］.新課程，2022（29）：120-121.