基于改進型哈里斯鷹算法的云制造服務組合優化方法研究

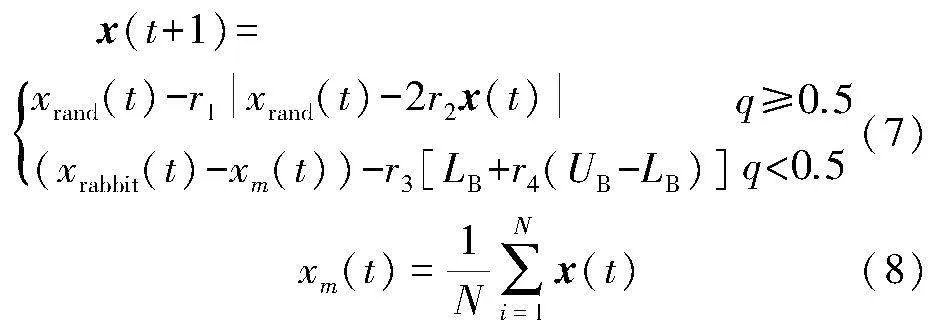
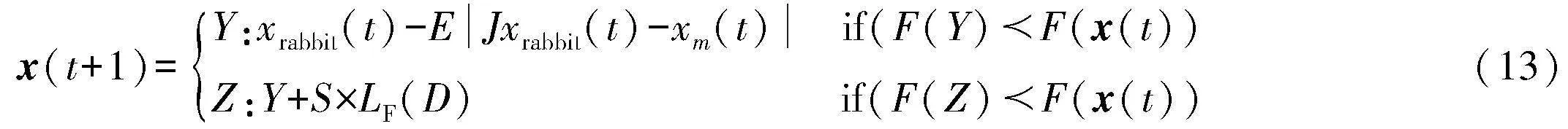
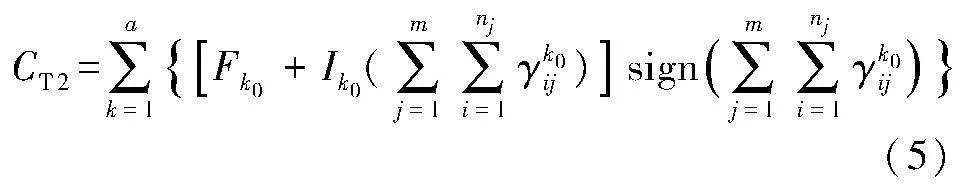
摘 要：云制造環境下，云平臺以制造服務組合的形式為個性化需求提供按需服務，可顯著提升訂單響應速度與提高資源利用率。采用哈里斯鷹算法構建制造服務組合，針對制造服務間物流轉運問題，建立獨特的編碼與解碼機制。為解決該算法存在早熟收斂問題，引入Logistic一維混沌系統，設計非線性逃逸能量更新機制和3種鄰域搜索策略。通過實驗驗證了改進后的哈里斯鷹算法在解決云制造服務組合優化問題時具有顯著優越性。

關鍵詞：云制造；服務組合；哈里斯鷹算法；任務調度

中圖分類號：TH164文獻標志碼：A文章編號：1671-5276（2024）03-0127-05

Research on Cloud Manufacturing Service Composition Method Based on

Improved Harris Hawks Optimization Algorithm

Abstract：In cloud manufacturing environment， the cloud platform provides on-demand services for personalized needs in the form of manufacturing service composition， which can significantly improve order response speed and resource utilization. This paper uses Harris Hawks optimization algorithm to construct manufacturing service composition， and establishes a unique coding and decoding mechanism for the logistics transfer between manufacturing services. In order to solve the premature convergence problem of the algorithm， the Logistic one-dimensional chaotic system is introduced， the nonlinear escape energy updating mechanism and three types of neighborhood search strategies are designed. Experiments verify the significant advantages of the improved Harris Hawk algorithm in solving the cloud manufacturing service portfolio optimization problem.

Keywords：cloud manufacturing; service composition; Harris Hawks optimization algorithm; task scheduling

0 引言

制造業技術的不斷突破推動了智能制造領域的蓬勃發展。為解決產能過剩并提高分布式制造資源的利用率，制造服務優化配置問題受到了密切關注。

目前針對制造服務優化配置問題已經有很多研究成果。DAO等［1］針對多企業的協同生產問題進行深入研究，提出一種獨特的遺傳算法，使得求解效率大幅提高。AKBARIPOUR等［2］針對分布式制造資源之間的物流問題對服務質量的影響進行充分研究，提出一種混合整數規劃模型。WANG等［3］在制造服務異常的情況下提出了一種新的編碼形式，可以對制造服務的異常情況進行動態重構。ZHANG等［4］提出了制造社區的概念與一種基于多目標優化的制造服務選擇和組合方法。LIANG等［5］提出一種基于深度強化學習算法的QoS-aware云制造服務組合優化方法，規避了元啟發式算法參數設置復雜的問題。王平等［6］提出一種基于雙層規劃模型的資源服務組合方法并采用云遺傳算法對模型進行求解。

目前大多數的優化配置模型對多個任務與多個子任務進行求解的較少。為此，本文提出一種基于改進哈里斯鷹算法，提高了全局的搜索能力，以最小化加工成本為目標，解決了分布式制造服務優化配置的問題。

1 制造服務優化配置問題分析

在云制造環境中，接受訂單的主體企業會將一部分訂單需求分配給合適的制造商，以減輕自己的生產壓力。因此需要在滿足制造任務要求的情況下，選取合適的制造商和合適的物流線路，使得所有任務的完工總成本最小，具體的問題研究模型如圖1所示。

為了能夠更加直觀地描述這一模型，現對該模型進行如下假設：

1）每個制造任務的不同制造子任務在不同制造商可以并行加工，不同制造任務的總裝任務也可以在主體企業并行完成。

2）不同的制造商與制造商之間，制造商與主體企業之間只有一次運輸。

3）貨物運輸時運載能力為無窮大，同時貨物都可以在一次運輸的過程中完成。

基于以上假設，本文建立以最小化成本為目標函數的模型，目標函數如下所示。

F=CM+CT（1）

式中：CM表示不同制造商的制造成本；CT表示在整個生產過程中由于物流而產生的成本。

式（1）表示所有任務的制造成本包括制造商和主體企業的制造成本兩部分；式（2）表示制造商的制造成本包括所有制造商的制造任務成本總和；式（3）表示物流成本包括制造商之間的物流成本（式（4））和運輸到主體企業之間的物流成本（式（5））兩部分。式中符號的描述如表1所示。

2 制造服務優化配置問題模型求解

2.1 編碼與解碼

本文主要考慮3個問題：多個制造任務、制造商的選擇和物流方式的選擇，因此種群編碼也與這3部分有關，如圖2所示。

圖2中制造任務由制造任務數目與制造任務子任務的數目有關。深色序列的上半部分表示制造子任務序列，深色序列的下半部分表示制造子任務的制造商。物流運輸選擇包括物流節點序列和物流節點決策變量兩個部分。物流部分的上方表示物流節點序列，其具體的節點序列與制造子任務序列有關，主要滿足以下規則：

1）運輸節點序列中有意義數目與第一部分的不重復制造商節點數有關；

2）運輸節點序列的順序與第一部分制造商節點的序列順序相同。

轉化后得到的物流部分編碼如圖3所示，無色部分無意義。深色上方序列表示運輸節點序列，深色下方序列表示對應節點的決策變量。

決策變量的解析主要滿足以下規則：

①具有相同的決策變量的運輸節點在同一次運輸過程中；

②不同的運輸節點在同一個運輸過程中，則物流路線總是從左側向右側運輸；

③所有運輸線路的終點都是主體企業；

④如果沒有相同的決策變量，則該制造商完成任務后直接運輸到主體企業。

根據以上規則，可以得出5條物流線路，其中4條分別是3號、5號、10號、6號直接運輸到主體企業；第5條物流線路是4號，首先運輸到1號然后再運輸到主體企業。

2.2 種群初始化

為了使算法的初始解具有更強的全局搜索能力，引入一維logistic混沌系統，如式（6）所示。

x（i+1）=μ×x（i）×（1－x（i））（6）

初始化流程如下（圖4）。

1）生成小數序列：隨機生成范圍為（0，1）的28個混沌個體與種群的28個維度相對應，完成第一步初始化。

2）整數化：取得的28個混沌個體，擴大10倍，并向上取整得到整數序列。

3）物流編碼處理：在整數序列中，前18位是制造商選擇部分，后10位是物流部分。將制造商選擇部分在不改變順序的情況下，除去重復的制造商，得到運輸節點序列。

2.3 種群更新策略

本文提出MHHO（Multi-HHO）算法，在HHO算法的基礎上通過改進逃逸能量更新策略和增加鄰域搜索策略兩種方式，增加算法的全局搜索能力，改進后的HHO算法（MHHO）流程如圖5所示。

搜索階段如式（7）和式（8）所示，在開始階段，HHO算法會根據初始種群，在可行解空間內進行搜索。

式中：x（t）和x（t+1）分別表示本次迭代和下一次迭代過程中哈里斯鷹的位置向量；xm（t）表示本次迭代中哈里斯鷹種群的平均位置；xrand（t）是獵物的位置；r1、r2、r3、r4和q是區間（0，1）中的隨機數；UB、LB分別表示變量的上限和下限；xrand是當前種群中隨機選擇的哈里斯鷹的位置；N表示種群數量。

由圖5可以看出，開發階段較為復雜，HHO算法會根據獵物的捕捉概率r和獵物的逃逸能量E兩部分確定哈里斯鷹的迭代點位。逃逸能量的更新如式（9）所示。

E=2×（1－t/T）×E0（9）

式中：E表示獵物的逃逸能量；E0表示區間（-1，1）的隨機數；t表示當前的迭代次數；T表示算法預設的最大迭代次數。當|E|≥0.5時表示有較多的逃逸能量。r≥0.5表示在本次捕獵中，獵物最終被追捕。基于這兩個參數，在這個階段包括4種迭代策略。

1）軟圍攻：當|E|≥0.5和r≥0.5時，如式（10）所示。

X（t+1）=Xrabbit（t）－X（t）－E|JXrabbit（t）－X（t）| （10）

式中J=2（1-r5）表示獵物嘗試逃離時的能量強度，其中r5（0，1）是一個隨機數。

2）硬圍攻：當|E|＜0.5和r≥0.5時，如式（11）所示。

X（t+1）=Xrabbit－EXrabbit（t）－X（t）（11）

3）漸進式軟圍攻： |E|≥0.5和r＜0.5，如式（12）所示。

式中：D表示種群的維度；S表示一個隨機個體；LF的Levy飛行函數；表示更優。

4）漸進式硬圍攻：當|E|＜0.5和r＜0.5時，如式（13）所示。

5）逃逸能量更新策略

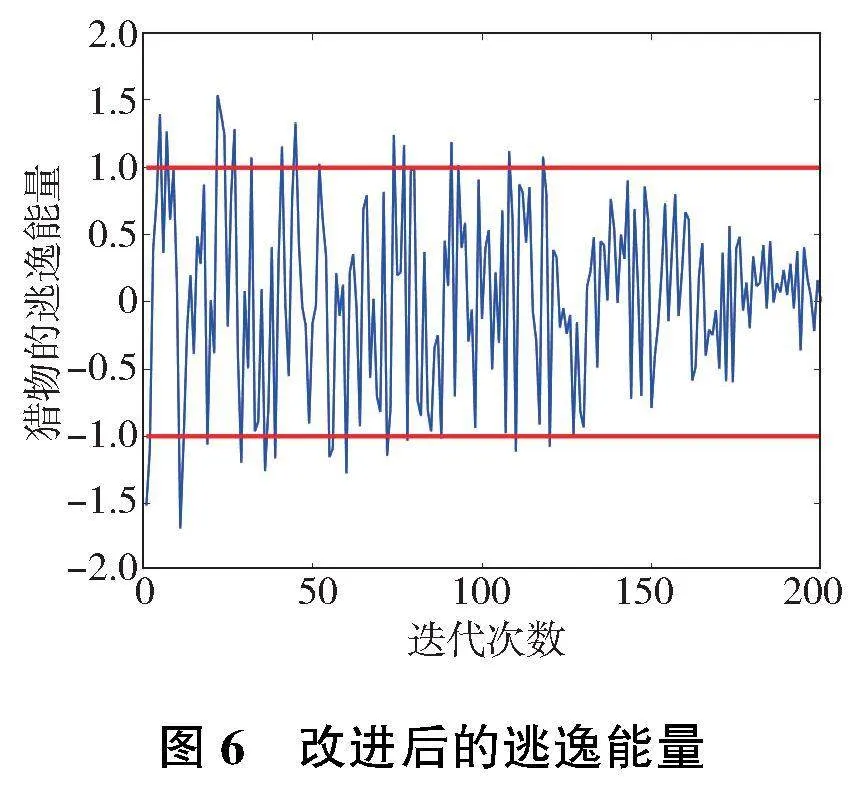
文中通過使用一種非線性逃逸能量更新策略，其逃逸能量更新如式（14）所示，曲線如圖6所示。

由圖6可以看出，改進的逃逸能量曲線中在120次迭代左右依然有一定的概率進入搜索階段，能夠在全局的范圍內搜索更優的可行解，大大提高了算法的全局搜索能力。

6）鄰域搜索策略

鄰域搜索通過不同種群個體進行交叉、置換等操作，尋找該個體附近的優秀編碼。在本算法中主要包括3種鄰域搜索策略：

策略1，隨機選擇1個個體，隨機選擇某個位置，將該位置的編碼重新生成；

策略2，隨機選擇2個個體，隨機選擇2個位置，將2個位置之間的編碼交換；

策略3，隨機選擇2個個體，隨機選擇位置，將指定位置的編碼進行交換。

3 仿真驗證與分析

3.1 算法設計

文中設計的制造服務優化配置仿真實驗包括3種情況：制造規模為3×10、4×10、5×10，表示制造任務數目分別為3、4、5個，制造商的數目為10個。其中制造任務1—5的生產周期分別為27 d、26 d、25 d、26 d和28 d。

3.2 仿真結果分析

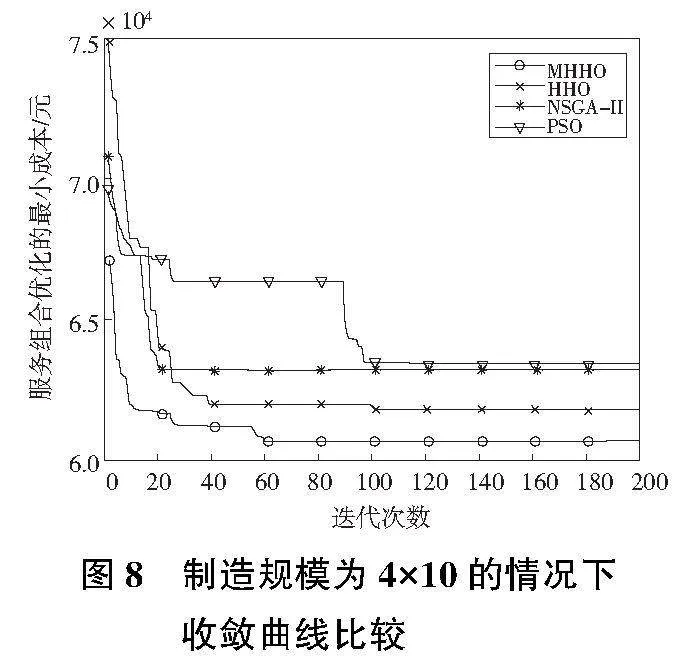
為了驗證文中MHHO算法的優越性，將相同的問題與HHO、PSO（particle swarm optimization）、NSGA-Ⅱ（non-dominated sorting genetic algorithm-II）4種算法在上述仿真環境中進行比較。仿真實驗利用MATLAB2021a進行程序編寫，運行環境為Win10系統，2.6GHz，16G內存。每個算法的種群規模為100，迭代次數選定為200次。收斂曲線對比如圖7—圖9所示。

從圖7—圖9中可以看出，MHHO算法具有最低的最小化成本，在不陷入局部收斂的情況下，具有最快的收斂速度。同時，由于引入Logistic一維混沌系統，MHHO算法在初始具有最低的適應度。MHHO算法的中期乃至后期都具有一定的搜索能力，并沒有出現局部收斂的問題。

將上述算法重復運行30次，最優解、平均解、平均收斂次數和平均求解時間等結果如表2所示。不同制造規模下MHHO算法都可以獲得更高質量的最優解和平均解。在平均收斂次數方面，MHHO算法稍劣于HHO和PSO，但是有效避免了陷入局部最優的問題。相較于NSGA-Ⅱ，MHHO算法的平均收斂次數更低，最優解與平均解的質量更高。MHHO算法的平均求解時間最長。但隨著制造任務數量的增多，平均求解時間與其他算法的差距越來越小。

4 結語

針對分布式制造服務優化配置問題，文中從制造任務數目、制造商選擇和物流方案三方面進行研究，建立優化目標模型，設計獨特的編碼與解碼方式。針對HHO算法全局搜索能力差的問題，從種群初始化、逃逸能量更新和鄰域搜索3個角度進行改進。最后，通過不同規模制造任務的案例，驗證了MHHO算法在求解質量、收斂速度方面的有效性和優越性。同時隨著制造規模的增加，MHHO算法將具有更強的優勢。

參考文獻：

［1］ DAO S D，ABHARY K，MARIAN R. An innovative GA for optimisation of integrated manufacturing-transportation scheduling in VCIM systems［J］. Operational Research，2020，20（3）：1289-1320.

［2］ AKBARIPOUR H，HOUSHMAND M. Service composition and optimal selection in cloud manufacturing：Landscape analysis and optimization by a hybrid imperialist competitive and local search algorithm［J］. Neural Computing and Applications，2020，32（15）：10873-10894.

［3］ WANG Y， WANGS， KANG L， et al. An effective dynamic service composition reconfiguration approach when service exceptions occur in real-life cloud manufacturing［J］. Robotics and Computer-Integrated Manufacturing，2021，71：102143.

［4］ ZHANG Y，TANG D B，ZHU H H，et al. A flexible configuration method of distributed manufacturing resources in the context of social manufacturing［J］. Computers in Industry，2021，132：103511.

［5］ LIANG H， WEN X， LIU Y， et al. Logistics-involved QoS-aware service composition in cloud manufacturing with deep reinforcement learning［J］. Robotics and Computer-Integrated Manufacturing，2021，67：101991.

［6］ 王平，肖涵，潘燕華. 基于雙層規劃的云制造資源服務組合［J］. 計算機集成制造系統，2022，28（1）：51-58.