解三角形常見題型例講

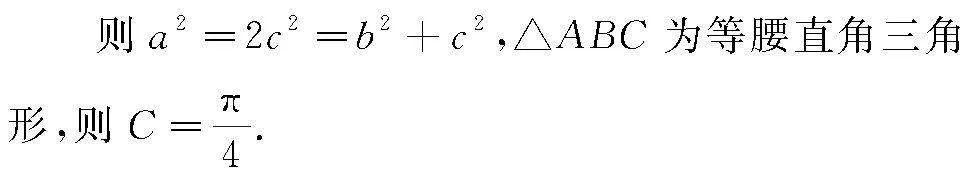
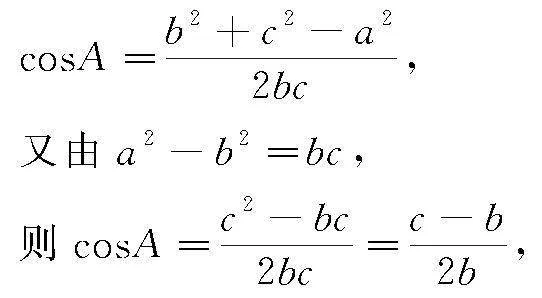
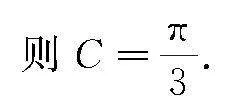
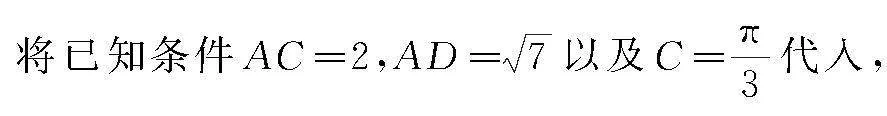
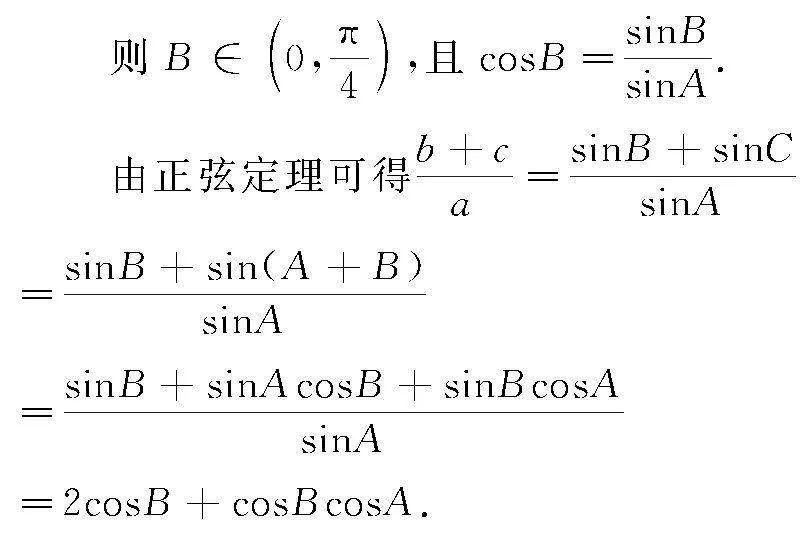
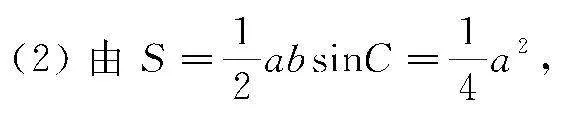
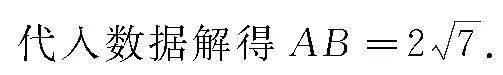
【摘要】解三角形是高中數學的重要知識點.依據要求解的問題可分為求邊長、求角度、求面積、求范圍四類題型.解答這四類題型主要運用正弦定理、余弦定理以及平面幾何、函數等知識.本文圍繞具體例題展示其中三種題型的解題過程，以供參考.

【關鍵詞】解三角形；高中數學；解題技巧

解三角形是高考的必考點.此類習題情境復雜多變，但無外乎求邊長、求角度、求面積、求范圍這四種題型.但是部分習題技巧性強，對學生分析以及解決問題的能力要求較高，因此，有必要對不同題型的解題過程進行探討，幫助學生積累解題經驗，促進學生解題能力與水平的提高.

題型1 求邊長

求三角形的邊長是解三角形中較為常見的題型.解題時需要吃透題意，必要情況下需要根據題干描述畫出草圖，明確各邊長的大致關系，注重正弦定理、余弦定理的活用.根據要求解的問題進行角與邊的靈活轉化，并在圖形的輔助下迅速找到解題思路.

即sinCcosA+sinCcosB=cosCsinA+cosCsinB.

則sinCcosA－cosCsinA=cosCsinB－sinCcosB.

則sin（C－A）=sin（B－C），

則C－A=B－C，

可得A+B=2C，又因為A+B+C=π，

（2）在△ADC中，由余弦定理得到：

AD2=AC2+CD2－2AC·CD·cosC，

得到CD2－2CD－3=0，

解得CD=3.

因為點D為BC的中點，

則BC=2CD=6.

在△ABC中，由余弦定理可得：

AB2=AC2+BC2－2AC·BC·cosC，

點評 該題涉及兩個小問，其中問題（1）需要運用正弦定理將給出的等式轉化為角度之間的關系，結合三角形的內角和等于π，可求出角C大小；問題（2）給出部分邊長，求AB的長，需要運用問題（1）中的結論以及余弦定理.當然運用余弦定理時還應根據求解的問題，靈活選取對應的三角形，通過求出三角形的公共邊，使得問題得以順利突破.

題型2 求角度

高中數學解三角形中求角度通常針對一般的三角形.求解時需要扎實掌握基礎知識，構建清晰的知識脈絡，理順基礎知識之間的內在聯系.根據題干創設的情境靈活運用正弦定理、余弦定理.需要注意的是運用三角函數確定角度時不能忽略三角形的內角和這一隱含條件.

例2 在△ABC中，A，B，C所對的邊分別為a，b，c，已知a2－b2=bc.

（1）證明：A=2B；

解 （1）由余弦定理可知：

即，b=c－2bcosA，

由正弦定理可得sinB=sinC－2sinBcosA，

即，sinB=sin（A+B）－2sinBcosA，

sinB=sinAcosB－cosAsinB=sin（A－B）.

又由A，B∈（0，π），

則B=A－B，則A=2B.

則2bsinC=a，

由正弦定理可得2sinBsinC=sinA=sin2B，

即，2sinBsinC=2sinBcosB，

又由sinB≠0，

則sinC=cosB，

又由B，C∈（0，π），

題型3 求范圍

求解三角形中某一參數，如角度、邊長、面積的取值范圍，要考查的知識點較749deb5e718020ecd2662ccc647ea6ce多，難度中等，需要根據題意靈活運用三角函數的有界性、函數的單調性、基本不等式等知識進行分析，尤其在計算的過程中應把握參數的取值范圍，確保計算結果的正確性.

例3 在△ABC中，A，B，C所對的邊分別為a，b，c，已知sinA=tanB.

即（b－c）（b+3c）=0，

即b=c或b=－3c（舍去）.

（2）由已知條件可得0<tanB<1，

由A為銳角，cosA>0，

點評 該題中的兩個問題難度均不小.其中問題（1）需要注重隱含條件的應用，尤其運用正弦定理、余弦定理，通過等量代換確定三角形的形狀求出角度.問題（2）在構建已知條件與要求解問題之間的關系后，通過換元將問題轉化為求函數在特定區間的單調性問題，運用函數知識便能順利求出取值范圍.

結語

綜上所述，求解解三角形三種題型的關鍵在于吃透題意，結合圖形在頭腦中形成對要求解問題的大致認識，深入理解正弦定理、余弦定理，結合三角形建立清晰的邊角關系，實現角與邊的靈活互化.同時，還應具備靈活的思維，注重三角函數恒等變形以及三角形內角、邊長關系等隱含知識的運用，必要情況下通過換元轉化成函數，借助函數性質加以求解.

參考文獻：

[1]關廣嚴.高中數學章節復習課的教學設計——以“解三角形”為例[J].中學數學，2023（19）：86-87.

[2]劉海濤.對一道高中數學聯賽解三角形問題的探析[J].數理化解題研究，2023（25）：15-18.

[3]蘇亞亞.例談三類解三角形問題的解法[J].語數外學習（高中版上旬），2023（04）：42.