公式歸納，多維應用

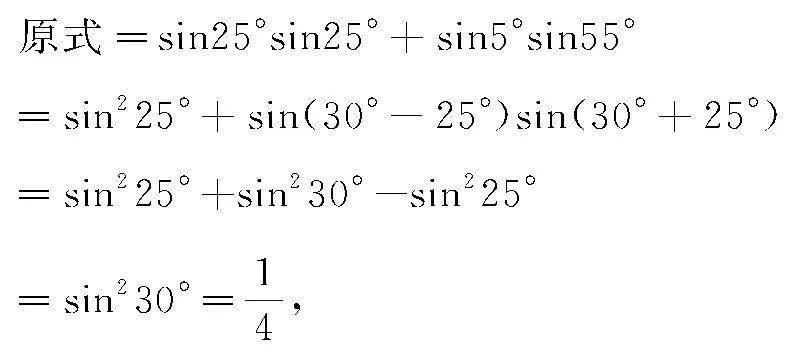
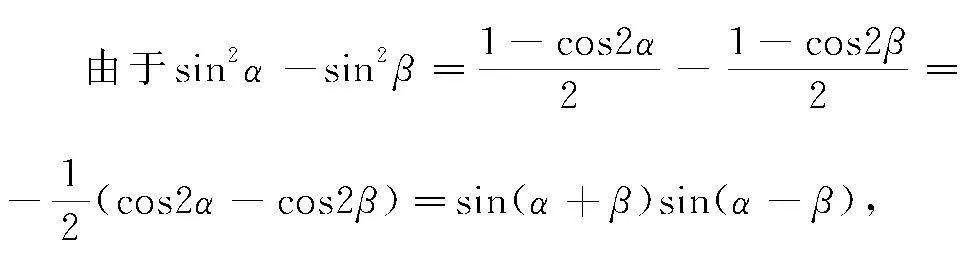
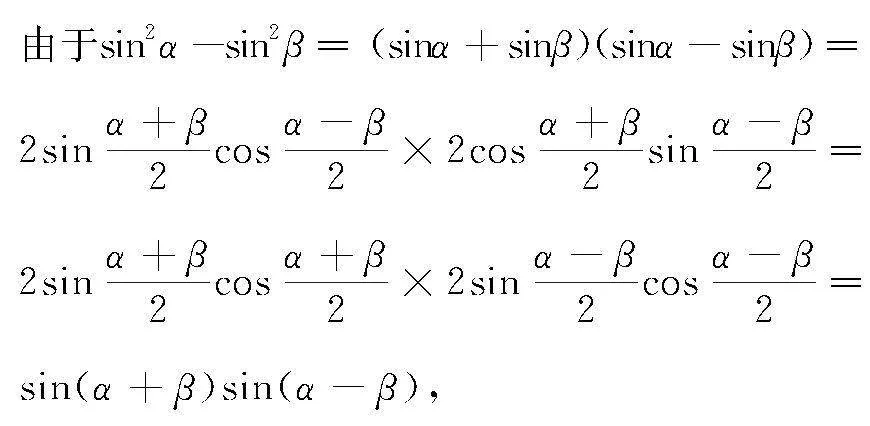
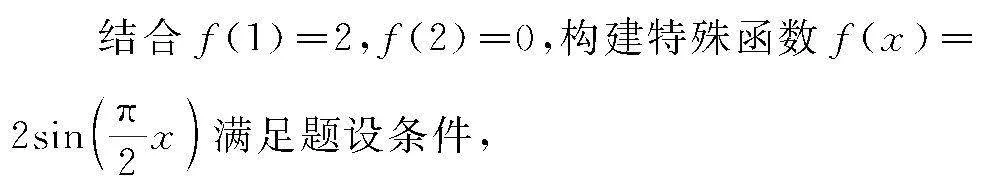
【摘要】三角函數中除了教材中的給出的一些基本公式，還有一些非常優秀的“二級結論”，在實際解題過程中有奇效．結合正弦平方差公式的展示、證明與拓展，并通過實例剖析該公式的多維應用，開拓數學思維，提升數學應用，引領并指導數學教學與復習備考．

【關鍵詞】三角函數；正弦平方差；高中數學

正弦平方差公式是三角函數基本公式的深入與拓展，是三角函數及其應用中的一個重要公式，形式優美，當中涉及三角函數及其對應的代數運算，具有較為廣泛的應用，是三角函數知識中的一個重要的“二級結論”，需要加以重視．

1 正弦平方差公式

1.1 公式

公式1 對于任意的實數α，β，都有sin2α－sin2β=sin（α+β）sin（α－β）成立．

1.2 公式證明

方法1 和差化積公式+二倍角公式法

故公式成立．

方法2 二倍角公式+和差化積公式法

由于sin2α－sin2β=1－cos2α2－1－cos2β2=－12（cos2α－cos2β）=sin（α+β）sin（α－β），

故公式成立．

方法3 兩角和差公式法

故公式成立．

正弦平方差公式的形式直觀，類似于代數中的平方差公式，是三角函數與代數知識的綜合交匯與有機拓展，對于解決一些相關的應用問題有妙處．

1.3 公式拓展

公式2 （余弦平方差公式）對于任意的實數α，β，都有cos2α－sin2β=cos（α+β）cos（α－β）成立．

在公式1的正弦平方差公式的基礎上，合理類比拓展即可得到以上余弦平方差公式．注意公式1與公式2之間的聯系與區別．

2 正弦平方差公式的多維應用

2.1 三角求值問題

例1 計算：sin25°cos65°+sin5°sin55°=．

分析 根據題設條件，無法直接利用三角函數及三角恒等變換公式等加以求值，觀察其中角的形式，借助誘導公式及角的加減運算加以變形，利用正弦平方差公式的轉化與應用，從而實現非特殊角的三角函數關系式的求值與應用．

解 依題，借助正弦平方差公式，可得

點評 借助三角函數關系式中角的形式與代數關系，觀察三角關系式的形式，綜合利用三角函數及其三角恒等變換公式等加以應用，是解決此類問題的關鍵所在．而在具體解題時，抓住問題的根本，巧妙利用正弦平方差公式來轉化，可以有效變形，實現問題的突破，得以有效求值．

2.2 解三角形問題

例2 在△ABC中，內角A，B，C的對邊分別為a，b，c，若sin2B－sin2C=sinA，則B－C=．

分析 根據題設條件，綜合正弦平方差公式、三角形內角和定理以及誘導公式等的應用，合理變形與轉化，進而得以化簡對應的三角關系式，得以確定對應的三角函數值，借助整體思維，得以確定相關角的代數式的大小．

解 依題sin2B－sin2C=sinA，

利用正弦平方差公式

sin2α－sin2β=sin（α+β）sin（α－β），

可得sin（B+C）sin（B－C）=sinA，

而sin（B+C）=sin（π－A）=sinA>0，

則有sin（B－C）=1，

而B－C∈－π，π，

點評 在實際解決一些相關的解三角形問題時，可以合理綜合三角函數、三角形以及解三角形中的相關概念、公式與性質等，巧妙交匯，綜合應用．這里借助正弦平方差公式進行合理變形，通過整體思維來分析并求解相關角的代數式的值．

2.3 抽象函數問題

例3 （2023屆江蘇省南京市高三（上）學情調研數學試卷（9月份））已知函數f（x），任意x，y∈R，滿足f2（x）－f2（y）=f（x+y）f（x－y），且f（1）=2，f（2）=0，則f（1）+f（2）+…+f（90）=（ ）

（A）－2. （B）0. （C）2. （D）4.

分析 根據題設條件，挖掘抽象函數的結構特征，吻合正弦平方差公式，合理聯想并創新構建三角函數模型，并利用特殊函數值加以配湊對應函數的系數，借助特殊值法加以轉化與應用，綜合函數的基本性質加以分析與求解．

解 依題f2（x）－f2（y）=f（x+y）f（x－y），吻合正弦平方差公式sin2x－sin2y=sin（x+y）sin（x－y），

則知該函數f（x）是以4為周期的函數，也是一個奇函數，有f（0）=0，

依f（1）=2，f（2）=0，可得f（3）=f（－1）=－f（1）=－2，f（4）=f（0）=0，

則f（1）+f（2）+f（3）+f（4）=0，

所以f（1）+f（2）+…+f（90）=22×f（1）+f（2）+f（3）+f（4）×22+f（1）+f（2）=2.

故選擇答案：（C）．

點評 借助抽象函數的結構特征與對應的公式形式構建聯系，通過特殊值法的應用來構建特殊函數模型，是解決一些相關問題中比較常見的一種思維方法．熟練掌握一些具有特定結構特征的基本初等函數類型，為解決此類問題的特殊函數模型思維提供理論依據，也是綜合創新應用的基礎．