問題情境視角下的高中數學建模教學設計與實踐

【摘要】在新高考背景下，數學建模作為高中數學教學的重要組成部分被賦予新的內涵.在日常的教學活動中，教師應當致力于發展學生的思維，培養他們解決實際問題的能力，提升他們的學科核心素養.為了達成上述教學目標，問題情境作為一種先進的教學方法被廣泛地應用于課堂教學.教師通過生動、有趣的問題情境設置以及循序漸進的問題串導引，使學生更新傳統的學習方式并形成對數學知識的新思考.

【關鍵詞】情境教學；高中數學；數學建模

隨著社會的發展，越來越多的教師意識到創新思維的重要性.為了將學生培養成全方面發展的高素質人才，教師積極引入多元策略并完善他們的建模思維，提升他們的建模能力，從定義來看，數學建模能力的培養離不開具體的問題.針對這一現象，教師將問題情境與建模能力的培養相聯系.本文將從問題情境的內涵出發，深入分析問題情境視角下高中數學建模教學設計原則和基本方法.

1 課程分析

本文基于一次函數、二次函數、指數函數、對數函數、冪函數在實際生活中的應用課程，設計了“公司獎勵機制”這樣一個問題情境用于建模教學，將現實問題與數學問題結合起來，引導學生建模并培養學生在情境中解決問題的能力.本課的問題情境為“函數模型應用實例”中的生活建模實例，將函數與生活實際聯系起來，在情境創設、分析教學、合作交流、小組展示、總結歸納與深化反思等活動中，逐步引導學生建立起了完整的數學模型，以解決實際問題，是一節指導學生從函數角度出發，使用數學知識、思想、方法，獨立建模并解決問題的課程.

2 教學策略

本課教學始終立足問題情境，構建完整課堂，以建模能力、解決問題能力為核心培養目標，從真實的問題情境出發，以問題情境創設，激發學生學習興趣，以分析探究、小組合作等環節，開啟深度學習，設計循序漸進、環環相扣的問題鏈，鼓勵學生自主思考、討論、分析各類函數的特征，并在現實問題中創設與之相關的數學模型，在師生互動、生生互動中，啟發數學思想、深化建模思想，達成教學目的.

2.1 創設情境，導入教學主題

課堂伊始教師要從日常生活中常見的問題導入本課主題.

情境導入：我們生活在繁華的城市中，每個路口都有紅綠燈，但各個紅綠燈的變化時間、持續時長都是不同的，大家有想過紅綠燈的秒數是怎樣設置的嗎？一天之中紅綠燈的秒數及紅綠燈的變化情況又是怎樣的呢？實際上，這些問題都可以從數學的角度來解釋.我們可以通過建模將這些問題與函數知識結合在一起.

通過生活中的常見事物為學生講解數學建模的基礎概念，讓學生了解建模，并能從生活出發使用數學思維解決實際問題，使學生感受數學在生活中的實際價值，是一種通過情境設立、情境導入的方式，引出本課主題以及本課主要問題情境的有效措施.

2.2 問題驅動，導入本課新知

隨著社會經濟的發展，越來越多的人開始關注企業的內部管理手段.在此過程中，獎勵機制作為一種以函數模型為基礎的管理辦法不僅包含了大量的管理理念，還承載著豐富的數學思想.

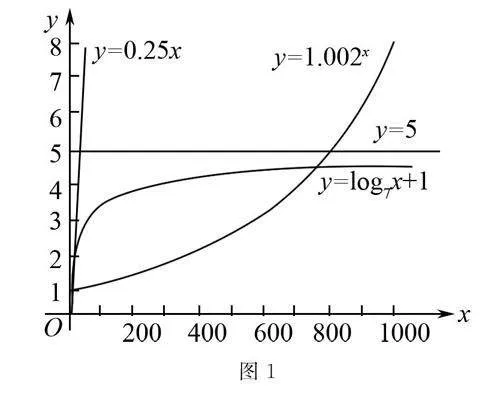
問題情境：某公司為了實現1000萬元利潤的目標，準備制定一個激勵銷售人員的獎勵方案.根據方案要求，當員工的銷售利潤達到10萬元時開始發放獎金且獎金隨銷售利潤的增加逐步提高.但考慮到公司經營的成本，獎金的總數不能超過5萬元，同時獎金不超過利潤的25%.假設y來表示獎金，x來表示銷售利潤.請從y=0.25x，y=log7+1，y=1.002x三個模型中選擇最符合企業發展的獎勵方法.

在本課中，學生將從現實問題中確定變量、探尋關系、建立模型、分析結論.結合該問題情境，教師創設了以下三個任務，作為本課的驅動性任務，并設立了相應的分組合作學習活動1和活動2.

任務1 請提煉出問題情境中的已知條件，并將其轉化為數學語言.

任務2 繪制y=0.25x，y=log7+1，y=1.002x三個函數圖象，觀察圖象，判斷并選擇出你認為最符合情境條件的函數模型.

任務3 問題解決后，反思在解題過程中的建模行為，并總結出建模的一般規律與過程.

活動1 任務1為學生獨立探究思考，以師生互動形式開展.

活動2 開展小組合作探究，各組學生應通過圖形計算器，在小組內繪制出三個不同的函數圖象，探究、討論后，應得出最符合條件的函數模型，并使用數學語言說明出為什么.

基于前期的問題情境，學生以小組為單位展開討論，并借助圖形計算器繪制出相應的模型（如圖1所示）.從模型的曲線來看，y=log7+1似乎更符合公司獎勵機制.

開啟任務3，強化學生反思，使其獨立思考并總結數學建模的一般規律.

2.3 深度探究，深化數學建模

從實際的生活案例來看，上述獎勵機制為簡單的、理想化的初等函數型的模型，因此，為了加強學生對數學模型特點的理解，教師從以下兩個方面入手調整模型建構，開啟下一輪探究活動，并設置了兩個新任務.

任務1 分析為什么y=log7+1更符合公司的獎勵機制.

任務2 以y=log7+1為基礎的獎勵機制是否存在缺陷，以及應如何通過模型的調整使獎勵機制更加科學化.

本環節依然以小組討論為主，要求學生在組內完成討論，得出結論，并匯總小組調研報告.討論結束后，由各組派出發言人表述本組討論成果.從實際的反饋來看，高中生在經歷一次函數、二次函數、指數函數、對數函數、冪函數的學習之后可以嘗試性地借助數形結合思想以及建模理念將具體知識點與實際生活相聯系.因此，基于高效的討論，學生提出兩個新的模型，即，y=5×10－5x2和y=1.0016x.為了讓數學模型更加貼合企業運轉規律，教師提出新的要求.

探究 如果把題中“在銷售利潤達到10萬元時，按銷售利潤開始進行獎勵”這句話刪掉，此前得出的模型還符合實際情況嗎？

在模型搭建的最后，教師從行業發展現狀出發，闡述銷售人員的薪資構成以及獎金情況.基于案例提示，學生重新以小組為單位探討獎勵機制的合理性.經過一系列的驗算，各小組不難發現，當x為0時，y=1.0016x這一模式便不符合要求.

本環節結束后，要求學生再次開展分組討論，根據本課經歷的所有建模過程，思考并匯總數學建模的實際定義.回顧此前對數學建模下達的定義、總結的一般規律，并做出最后調整，由教師提問檢測，得出“數學建模是應用數學思想、知識與方法，通過建立數學模型解決實際問題”這一結論，讓學生在相對開放且真實的情境中發現問題、解決問題，并掌握使用數學建模的方法，以教師總結與師生最后一次交流、反思結束本次課堂.

3 教學思考

3.1 問題情境的價值

3.1.1 問題情境對學生學習的意義

一直以來，問題是培養學生創新思維的起點.借助科學、合理的問題，學生一邊調動知識積累回答問題，一邊在回答問題的過程中完善知識架構、學習架構.在新高考背景下，越來越多的教師意識到提問的重要性，意識到情境對提問的重要性.為了最大程度地培養學生的數學思維，問題情境作為一種先進的教學策略開始被廣泛地應用于課堂教學.值得一提的是，創新思維的終點在于讓學生自主發現問題、分析問題、解決問題.因此，教師亦可以嘗試性地將提問的主動權交給學生.憑借豐富的數學任務，學生嘗試著自主提問、自主創新問題的解決之道.

3.1.2 問題情境對建模教學的價值

基于問題情境的建模教學包含兩部分.其一，教師借助與學生息息相關的教學情境提出問題；其二，學生借助問題內容總結具體概念，實現知識點的應用、遷移.區別于以往的教學模式，問題情境下的建模教學具有以下幾點優勢.首先，問題情境下的建模教學兼具趣味性、教育意義.由于教師選取的情境均與生活、與社會發展息息相關，所以，學生可以快速進入學習狀態.雖然，高中生已具備成熟的抽象邏輯思維，但抽象性較強的建模活動無疑會增加他們的課業壓力.這時，問題情境的適時插入不僅能調動學生的學習積極性，還能讓他們沿著問題情境深入感受建模的魅力.其次，問題情境下的建模教學具備鮮明的“生本”特色.所謂的“生本”特色就是堅持“以學生為主體”.在循序漸進的問題中，學生通過高效的小組合作分析問題、解決問題.一般來說，小組合作亦是產生新問題的過程.通過新問題的提出、分析、解決，學生逐步提升自己的學科核心素養.

3.2 問題情境應用的反思

3.2.1 忽略實際應用

重視理論知識，忽略實際應用是教師在開展數學教學，開展數學建模教學時經常會遇到的問題.雖然，越來越多的教師意識到創新思維的重要性，意識到建模思想的重要性，但是，從實際的教學效果來看，教師仍習慣于傳統的教學模式，即借助灌輸式、填鴨式的教學方式講解課本知識.在此過程中，學生處于被動地位且被動地跟隨教師的引導增加知識積累.久而久之，學生不僅會喪失主動構建數學模型的意識，還會喪失知識應用的能力.

3.2.2 考核方式單一

基于數學建模教學，傳統的評價方式已無法滿足學生的學習需求、心理訴求.然而，從實際的教學效果來看，教師習慣性地以自己為主體并按照結果式評價考量學生的學習情況.然而，建模教學的考核不應局限于期末考試成績，不應局限于“學生是否掌握某一具體的知識點”.為了最大程度地發揮問題情境在高中數學建模教學設計中的效用，教師可以擴充評價主體并通過高效的生生互動提升彼此質疑的能力.

3.3 問題情境應用的優化策略

3.3.1 堅持民主

其一，鼓勵學生質疑，鼓勵他們提出問題.在以往的教學模式中，教師將自己視為課堂教學的主體并單向性地傳遞具體知識點.久而久之，學生就會習慣于被動地接受知識點，從而喪失創新意識，喪失提升建模思想的機會.一般來說，高中生已具備成熟的抽象邏輯思維，所以，自由且寬松的氛圍能夠讓他們大膽地提出自己的質疑.在此過程中，教師要肯定他們提問的態度，重視他們的提問內容，與其他學生共同解決某一具體的問題.只有當學生意識到自己是被尊重的，被重視的之后，他們才能積極參與課堂互動，進而提升建模思維、創新思維.其二，以方向性的引導鼓勵學生分享自己的所思所想.當教師預留出充分的探索時間和空間后，學生或以個體為單位，或以小組為單位分析問題、解決問題.針對形形色色的問題，教師予以方向性的引導.借助方向性的引導，學生既能知曉大致的修正方法，又能知曉自己的努力方向.

3.3.2 遵循學情

教師在搭建問題情境之前要積極了解學生的學情.一般來說，學生學情處于不斷變化、發展的態勢.因此，教師可以制定動態化的學情檔案.其次，高中生已具備一定的探索能力，因此，教師需要定期評估他們的最近發展區.從課程標準來看，不同年級的學生其數學能力均是不同的.為了確保問題情境符合數學建模思想的培養，教師不斷提升自己的教學經驗并思考：怎樣的問題情境可以在調動學生學習積極性的同時提升他們的建模能力？

4 結語

“建模”作為一種先進的數學思想不僅體現了數學的學科特點，還是學生解決數學問題，解決實際問題的主要參考.在日常的教學活動中，教師緊扣教材內容并提供豐富的建模機會.一般來說，建模能力的培養講求長期且系統，因此，學生可以在豐富的學習活動中提升創新意識及綜合素養.

參考文獻：

[1]謝菊連.高中數學課堂中如何培養學生的數學建模能力[J].高考，2022（34）：108-110.

[2]高照穎，趙寶江.高中數學建模教學策略及案例分析——以《函數模型應用（二）》為例[J].新課程導學，2022（33）：24-27.

[3]李猛.關于高中數學建模教學的實踐[J].新課程教學（電子版），2022（22）：104-105.

[4]張新艷.高中數學建模：先理解，后實踐[J].數學教學通訊，2022（33）：53-54.

[5]張蓮聯.基于深度學習的高中數學建模教學實踐研究——以高速公路車流量預測為例[J].福建中學數學，2022（11）：44-47.