基于GM-RBF組合模型的BDS-3衛星鐘差短期預報

唐彥 李豫 李特

摘? 要：針對衛星鐘差具有趨勢項和隨機項變化的特征問題，該文提GM－RBF組合模型的方法。該模型首先用GM（1，1）提取預處理后的衛星鐘差趨勢項部分并進行建模預報，得到相應的殘差序列，通過RBF神經網絡訓練用灰色模型預報所獲得的殘差序列，然后將GM（1，1） 模型的鐘差后續預報值與RBF神經網絡的殘差預報值對應相加可得組合模型的預報結果。為驗證組合模型的有效性和可行性將組合模型預報結果與GM（1，1）模型、ARIMA模型、RBF神經網絡模型預報結果進行對比實驗。實驗結果表明，組合模型預報精度要高于其他單一模型，其在不同時段的平均預報精度可提高46.4%～86.2%。

關鍵詞：BDS衛星鐘差? 灰色模型? RBF神經網絡? 組合模型? 鐘差預報

中圖分類號：P228.1

Short-Term Prediction of BDS-3 Satellite Clock Errors Based on the GM-RBF Combined Model

TANG Yan1? ?LI Yu2? ? LI Te3

（1.Xinjiang Institute of Engineering， Urumqi， Xinjiang Uyghur Autonomous Region， 830000 China；2.Yingkou Chuangxue Jiaoyu， Yingkou， Liaoning Province， 115000 China；3.Heilongjiang Institute of Technology，Harbin，Heilongjiang Province，150000 China）

Abstract： In order to address the eigenproblem of the change of the trend term and random term of the satellite clock error， this paper proposes a method of the GM-RBF combined model. First， this model uses GM（1，1） to extract the pre-processed trend term of the satellite clock error， conducts modeling and forecasting to obtain the corresponding residual sequence， and uses the grey model to predict the obtained residual sequence by RBF neural network training. Then， the prediction result of the combined model can be obtained by adding the subsequent prediction value of the clock error of the GM（1，1） model and the residual prediction value of the RBF neural network. In order to verify the validity and feasibility of the combined model， the prediction results of the combined model are compared with those of the GM（1，1） model， the ARIMA model and the RBF neural network model. Experimental results show that the forecast accuracy of the combined model is higher than that of other single models， and that its average forecast accuracy can be increased by 46.4% ～ 86.2% in different periods.

Key Words：BDS satellite clock error; Grey model; RBF neural network; Combination model; Clock error forecast

北斗衛星導航系統（BeiDou Navigation Satellite System，BDS）作為世界上的第三個已完全發展成熟的導航系統，對于提升國家實力具有重要意義。然而，如果北斗衛星時間誤差達到1 ns，將會導致約0.3 m的距離測量錯誤。為了有效地減少這種影響并進一步優化定位準確性，對BDS衛星時鐘偏移預測的研究變得至關重要。這不僅能迅速、精準地增強定位性能，還能為我國帶來顯著的社會效益與經濟效益，從而推動國家的整體發展[1]。

北斗精密鐘差的獲取具有較為嚴重的滯后性，難以實時獲取，這在一定程度上限制了BDS的基礎服務，因此選擇合適的方法和模型對鐘差進行預報具有重大意義和廣闊的應用價值。目前，許多國內外研究人員開發了不同的預報模型，主要包含灰色模型、自回歸滑動平均模型、神經網絡模型、二次多項式模型等[2]。呂棟等[3]提出基于思維進化算法優化BP神經網絡組合模型，結果表明，采用MEA算法獲取較好的初始化權值和閾值等參數，提高了衛星鐘差建模的精度，其預報精度明顯高于其他3種傳統模型。王建敏等人[4]將GM（1，1）模型和AR（p）模型有機組合，極大地提升模型的精度和適應性，其組合模型預報精度可達1 ns之內。于燁等人[5]通過利用GM（1，1）和MECM模型有效組合，很大的程度上對殘差進行了修正，相對于其所用的單一模型預報精度提升接近兩倍。

由于上述鐘差預報方法大多用于GPS衛星，而BDS衛星鐘差預報研究相對不夠廣泛，因此本文利用灰色模型與RBF神經網絡模型的特點，提出了一種基于誤差修正的GM－RBF組合模型的鐘差預報方法，并與其他3種單一預報模型進行對比，證明了組合模型的可行性和優越性。

1? 模型基本原理

1.1? GM（1，1）模型建立

灰色模型在處理信息不全面、數據量較小且混亂的時間序列上表現出獨特性，并且容易進行驗證。此外，它也無須顧及分布規律或趨勢因素，所以非常適合用于鐘差數據序列的建模[6]。設預處理后的鐘差序列，對鐘差序列做一次累加，得到生成新的鐘差序列數列為其中：

式（1）中：k為參與預報的衛星鐘差序列數據的個數。由數據可以構成GM（1，1）白化形式的微分方程為

式（2）中：a稱為發展系數；u稱為灰作用量。其離散化的矩陣方程可以表示為

其中，，

矩陣方程（5）的最小二乘解為

其中，， 分別為Ｄ、a、u的估計值，將（4）式代入（2）式得

對時間響應函數（2）式求解為

原始鐘差預測模型方程為得

原始序列的一般形式為

式（8）中：t為預報個數。根據式（1）可預報未來任意時刻的鐘差序列。

1.2? RBF神經網絡模型

徑向基函數（Radical Basis Function，RBF）網絡用RBF作為隱單元的“基”構成隱含層空間，再將輸入矢量直接映射到隱空間，不需要用權連接。當RBF的中心點確定以后，這種映射關系也隨之確定[7-8]。

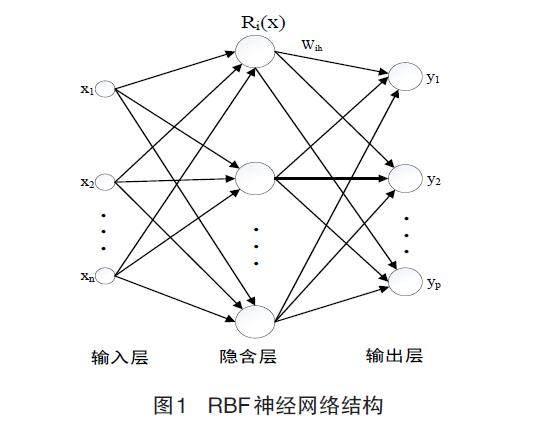
在RBF神經網絡中，必須了解的參數有三項：基函數的中心、方差及其隱含層至輸出層的權值，如圖1所示。

RBF解算具體實現過程如下：

（1）解算RBF基函數中心，在進行預測中RBF核函數選擇高斯函數：

式（9）中：為歐式距離范數；為激活函數中心；為方差；為輸入向量。

（2）計算隱藏層基函數的標準偏差。為避免RBF過尖或過平，以下是計算標準偏差的公式：

式（10）中：是選定的中心最大距離；為隱含層節點數量。

（3）采用最小二乘法計算隱含層與輸出層之間的權值，公式如下：

式（11）中：為隱含層與輸出層之間的權值。

（4）解算RBF網絡輸出：

式（12）中：輸入樣本所對應的鐘差數據。

2? 組合預報模型

傳統的GM和RBF組合方式是簡單的串并聯結合。由于衛星鐘差的真值是通過預測值加上殘差得出的，因此，把衛星鐘差看作由兩個主要因素構成：一個是趨勢項，另一個則是隨機項。本文以誤差補償作為組合的原理，改進傳統的組合模型方式，綜合GM所需建模數據少和RBF可有效挖掘復雜系統退化信息的優點，從而創建了一個新的衛星鐘差預測模型。

取n組數據進行組合模型建模，具體步驟如下所述。

（1）對衛星鐘差觀測數據做前期預處理。去除異常鐘差值，并使用線性插值法補全去除的異常值。

（2）利用GM（1，1）提取預處理后的前m組（m

（3）取，求模型殘差建模，即衛星鐘差的隨機項部分。

（4）以為RBF神經網絡的訓練樣本集，進行外推，求出衛星鐘差的隨機項部分的預報數值。

（5）將RBF神經網絡的隨機項序列預報值與其對應的GM（1，1）模型趨勢項序列預報值相加可得組合預報值。

3? 算例分析

3.1? 數據來源

為了驗證組合模型預報性能優于其他單一模型，通過IGS服務器分別下載了兩個時間段2019-12-22至2019-12-23與2020-01-18至2020-01-19采樣間隔為15 min的共4 d的北斗精密衛星鐘差數據。其中兩個時間段的鐘差數據均取前1 d作為建模數據，后1 d作為驗證數據。由于BDS-3搭載兩種不同星載原子鐘，因此分別在兩個不同時間段各取一個氫鐘與銣鐘的衛星。選取前一時間段的C25、C33與后一時間段的C26、C37衛星數據進行試驗和分析并將衛星預報結果進行詳細闡述。

3.2 方案設計

對C25、C26、C33、C37鐘差序列分別選用灰色模型（Gray Model，GM） 、自回歸滑動平均（Auto-Regressive Moving Average Model，ARIMA）模型、RBF神經網絡模型和GM－RBF組合模型，分別對6 h、12 h、18 h和24 h的衛星鐘差進行預報。

3.3? 數據預處理

一般情況下，衛星鐘差的頻率都數據，并且相位分布模式更接近線性分布，粗差隱藏在相位數據中難以發現 。因此使用中位數粗差探測法進行粗差檢測時，需要先將相位數據轉化為頻率數據 。公式如下：

式（13）中：為第i個歷元的頻率值；為第i個歷元的相位值；為歷元間的采樣間隔。通過式（13）把相位轉變換成頻率。

用中位數粗差探測法對原始鐘差序列進行粗差探測，具體公式如下：

式（14）（15）中：為衛星的頻率；為頻率的中位數；為適合數據序列的正整數；MAD為中位數絕對偏差；median為中位數運算符。

由式（14）（15）可知，當頻率的絕對值大于頻率序列的中位數加上頻率序列偏差絕對值的中位數的正整數倍時，則把該頻率據看作粗差，否則將看作正常序列。使用線性插值法補全剔除粗差后的數據，最后得到預處理后的頻率。公式中的b需要根據實際情況來進行多次調試，直到粗差被剔除。本文多次調整b值，最終選擇b=3進行判定。限于文章篇幅，本文以C25為例。

如圖2所示，從第一天結束至第二天開始，鐘差數據顯示出明顯的天跳變現象情況，原因在于IGS提供的精密鐘差和相關設備的數據處理方式是以天作為單位并按照單天為弧段進行計算。由于容易受到大氣的干擾、多徑效應等影響，導致接收機接收到的其他誤差和自身的鐘差產生系統誤差。同時，因為衛星鐘差本身是一個相對量，所以會導致連續兩天內的接收器鐘差產生跳變，從而引發了IGS精密鐘差產品中的天跳變現象。在經過預處理后頻率數據未存在特別明顯的極值，頻率波動相對穩定，有效地剔除了粗差，表明了預處理效果相對顯著。

3.4? 組合模型具體實現

將衛星鐘差數據兩個時間段的前一天作為實驗數據，選擇前48個歷元的數據為鐘差序列趨勢項部分建立灰色預報模型，并預報后面12 h鐘差數據，并用真實鐘差值減去預報值的隨機項，把隨機項作為RBF神經網絡的訓練樣本集。采用滑動窗口方法對鐘差數據集進行劃分，每次向右滑動一步，每次滑動選取5個歷元鐘差數據，輸出的鐘差數據為第6個歷元數據，剩余的96個歷元數據利用滑動窗口方法進行預測。因此，輸入層神經元個數為5個，輸出層神經元個數1個，隱含層神經元個數通過newrb函數輸入神經元的最大數目進行訓練即可確定。

3.5 預報結果與分析

使用上述方案進行建模， 通過IGS發布的事后精密衛星鐘差與組合模型和單一模型預報的鐘差值進行對照，用均方根誤差（RMS）來作為標準分析預報精度。其RMS計算公式如下：

式（16）中：為事后精密衛星鐘差；n為歷元個數；為預報的衛星鐘差。實驗結果如表1所示。

從表1的鐘差預報統計量得出以下結論。

（1） GM（1，1）模型、ARIMA模型、RBF神經網絡模型和GM-RBF組合模型都可以適用于北斗精密衛星鐘差短期預測。在兩個時間段內，組合模型預測精度均高于單一模型。

（2）對未來一天不同時段的衛星鐘差進行預報，GM-RBF組合模型的預報精度最高，相較于GM（1，1）模型平均預報精度分別提升了78.7%、82.1%、80.0%、71.9%；相較于ARIMA模型平均預報精度分別提升了86.2%、84.8%、80.3%、73.3%；相較于RBF神經網絡模型平均預報精度分別提升了47.4%、51.2%、53.0%、46.4%。

（3）在單一預測模型當中，GM（1，1）模型與ARIMA模型的預測精度相對較差，其平均預報精度均在1.8 ns以上，而且數據存在顯著波動的特征。在RBF模型與組合模型的預測結果中，RMS伴隨著預測歷元個數的增加而增加，并且組合模型的預報誤差在0.9 ns以下，模型顯示出良好的穩定性和更高的預測精準度，這比任何單獨模型都要優秀。隨著預測時長的增加，組合模型受RBF神經網絡模型影響較大，誤差增量逐漸增加。組合模型相比單一模型平均預報精度提高了46.4%～86.2%。

（4）對未來6、12、18、24 h的衛星鐘差進行預報，其中GM（1，1）模型在BDS-3星載氫鐘的平均預報精度為0.92 ns、0.97 ns、1.01 ns、1.09 ns；ARIMA模型在BDS-3星載氫鐘的平均預報精度為1.13 ns、1.10 ns、1.11 ns、1.15 ns；RBF模型在BDS-3星載氫鐘的平均預報精度為0.18 ns、0.24 ns、0.34 ns、0.51 ns；組合模型在BDS-3星載氫鐘的平均預報精度為0.14 ns、0.17 ns、0.20 ns、0.29 ns。GM（1，1）模型在BDS-3星載銣鐘的平均預報精度為1.22 ns、1.55 ns、2.04 ns、2.67 ns；ARIMA模型在BDS-3星載銣鐘的平均預報精度為1.14 ns、1.38 ns、1.73 ns、2.22 ns；RBF模型在BDS-3星載銣鐘的平均預報精度為0.52 ns、0.77 ns、1.05 ns、1.43 ns；組合模型在BDS-3星載銣鐘的平均預報精度為0.15 ns、0.21 ns、0.38 ns、0.73 ns。因此，在相同的模型中，BDS-3星載氫鐘的短期預測性能優于銣鐘，這與氫鐘本身卓越的短期預測性能緊密相連。

4 結語

針對衛星鐘差具有趨勢項和隨機項變化的特征，提出了一種基于GM－RBF組合預報模型。該組合模型是通過對兩種單一模型的綜合利用，首先用GM（1，1）提取預處理后的衛星鐘差趨勢項部分并進行建模預報，并得到相應的隨機項部分用RBF神經網絡進行建模預報，最后將兩種模型的預報值相加得到組合模型預報值。通過對4種模型預報精度進行分析可知，GM-RBF模型簡單， 在預報時長增加時，誤差曲線穩定性較好，預報結果比其他單一模型精度更好，證明了組合模型在BDS-3衛星鐘差短期預報中的有效性及穩定性是較佳的，可用于BDS-3衛星鐘差的高精度預報。

參考文獻

[1]楊元喜，李曉燕.微PNT與綜合PNT[J]，測繪學報，2017，46（10）：1249-1254.

[2]雷雨，趙丹寧.基于線性組合模型的導航衛星鐘差預報[J].測繪技術裝備，2013，15（3）：38-40.

[3]呂棟，歐吉坤，于勝文，等.基于MEA-BP神經網絡的衛星鐘差預報[J].測繪學報，2020，49（8）：993-1003.

[4]王建敏，李特，謝棟平，等.北斗精密衛星鐘差短期預報研究[J].測繪科學，2020，45（1）：33-41.

[5]于燁，張慧君，李孝輝，等.基于GM（1，1）和MECM組合模型的GPS衛星鐘差中短期預報[J].天文學報，2018，59（3）：19-30.

[6]程博.GPS/BDS精密單點定位及短期鐘差預報[D].阜新：遼寧工程技術大學，2021.

[7]徐麗麗，李洪，李勁.基于灰色預測和徑向基網絡的人口預測研究[J].計算機科學，2019，46（S1）：431-435.

[8]李宏達.基于多模GNSS精密單點定位的大氣可降水量反演研究[D].貴陽：貴州大學，2020.